一种改进诱导因子计算方法的叶素动量理论体积力模型
2024-01-19王明哲王建华万德成
王明哲,王建华,万德成
(上海交通大学a.船海计算水动力学研究中心(CMHL);b.船舶海洋与建筑工程学院,上海 200240)
0 引 言
在进行螺旋桨与其他结构物相互作用的数值模拟中,螺旋桨模型因为复杂的旋转运动以及复杂的几何结构,往往会需要较长的计算时间和较大的存储误差成本。体积力模型通过将螺旋桨与流体的相互作用力模化为分布在流场中的体积力,作为源项直接参与动量方程的求解,是代替真实螺旋桨模型的减小计算成本的有效手段,在船桨相互作用、桨舵相互作用以及船舶操纵性能模拟等方面得到了大量的应用。
作为一种简化模型,体积力模型的复杂性与准确性是影响其应用性的关键因素。叶素动量理论模型作为一种复杂性与准确性适中的体积力模型,具有较大的应用潜力[1-3]。
使用叶素动量理论计算得到的螺旋桨性能与真实螺旋桨模型性能接近,但难以在不同工况下保证相同的准确性。Benini[4]研究了使用叶素动量理论模拟船用螺旋桨的适用性,其中叶元参数由基于势流理论的二维叶元性能计算软件XFOIL 计算,结果表明使用叶素动量理论计算螺旋桨性能的最小误差为2%,但误差对进速系数的变化较为敏感;Phillips[1]使用基于叶素动量理论的体积力模型进行了KVLCC 的PMM 试验数值模拟,忽略了螺旋桨载荷分布的周向不均匀性,最后发现在小舵角工况下船体侧向力与艏摇力矩预测误差在(2~3)%以内,而当舵角增加时预报误差增大。种种研究表明,可以通过修正手段提高叶素动量理论体积力模型的准确性。
叶元参数准确性与叶元水动力计算方法是影响叶素动量理论体积力模型的关键因素。对于叶元参数,已存在部分经验公式方法用于修正非设计工况下的螺旋桨叶元参数,但无法保证此修正方法对于不同桨型及工况的适用性[5-6]。叶元水动力计算方法包括直接使用当地速度以及迭代计算诱导因子。冯大奎等[7-10]基于KP505 真实螺旋桨模型的敞水试验模拟结果建立了叶元参数与当地速度的关系,分析了不同叶数下叶元的性能变化,进行了KCS 模型尺度与实尺度在设计航速下的自航试验模拟,模拟结果表明体积力模型与真实螺旋桨得到的自航因子结果吻合;Tokgoz[11]通过叶元参数的一般表达式与直接使用当地速度方法进行了AU螺旋桨敞水与斜流试验模拟,结果表明敞水条件下得到的螺旋桨扭矩误差较大,且进速系数越低准确性越低。
传统的诱导因子迭代方法基于理想流体的动量理论推导得出,未考虑粘性求解器中的粘流环境[2]。Villa[12]拟合了单个进速工况下桨叶周向平均载荷的径向分布函数,其中桨叶载荷由敞水实验得到,并将此载荷分布作为体积力分布与RANS 求解器结合,结果表明该体积力模型与真实螺旋桨模型作用下的尾流速度分布吻合程度高,证明了按照真实螺旋桨载荷分布的体积力模型可以得到预期的诱导速度场。但此种方法需要已知工况,无法处理来流速度变化的非定常及非均匀流场。傅慧萍[13]使用HO模型模拟了KCS船自航,发现进速与桨盘面当地速度接近线性关系。此研究结果表明在得到当地速度的情况下,可以通过此对应关系根据桨盘面当地速度反推进速,进而得到粘流条件下桨盘面各处诱导因子大小。
本文通过不同进速下螺旋桨敞水试验的CFD 数值模拟,得到在粘性作用与叶间干扰作用下的螺旋桨各叶元参数,并依据此叶元参数得到符合真实螺旋桨载荷径向分布的投影盘,进而得到此投影盘作用下各进速的敞水诱导速度场以及桨盘面处各位置的当地速度,最终通过当地速度与进速计算诱导因子分布。此诱导因子分布将植入叶素动量理论体积力模型,避免了诱导因子的迭代求解,并通过KP505螺旋桨真实模型与体积力模型的敞水试验验证本文的体积力改进方法。
1 数值方法
1.1 控制方程
本文使用改进的叶素动量理论体积力模型与真实螺旋桨进行螺旋桨敞水试验的数值模拟,使用的基础数值求解器为开源平台OpenFOAM 中的pimpleFoam 与pimpleDyMFoam,其中pimpleDyMFoam用于真实螺旋桨模型数值模拟,pimpleFoam 则用于实现体积力模型代码在粘流求解器中的植入。对于粘性不可压缩流体,控制方程为
式中,p为压力,ρ为流体密度,μ为粘性系数,ui为速度分量为雷诺应力。本文使用湍流模型封闭含有雷诺应力项的方程。对于最适用于螺旋桨敞水试验数值模型的湍流模型仍无定论[14],文中所使用的为k-ωSST 湍流模型,这种湍流模型针对根据各区域到壁面距离的变化在对应位置计算时激活不同的湍流变量控制方程形式,是一种应用性较广的方法[15]。(fε)i为体积力源项,由单独的叶素动量理论体积力代码计算得到[16],在使用体积力模型进行数值模拟时激活此项。体积力模型与真实螺旋桨模型均使用非定常模拟,用以验证体积力模型在处理非定常问题时的计算能力。速度场与压力场的解耦使用PIMPLE 方法,体积力源项的计算采用显式方法,即首先利用上一时间步的速度场计算体积力分布,再使用得到的体积力分布计算当前时间步的速度场。
1.2 叶素动量理论
每次完成控制方程的求解后,将进行一次叶素动量理论程序的计算以求取体积力分布。文中各叶元体作用于流场中称为致动点的位置,致动点的位置不随流场的迭代而发生改变,即螺旋桨转速仅为计算叶元体水动力性能的参量。致动点处的叶元体水动力在每个时间步根据瞬时当地速度计算,且各致动点互不影响,因此对于船桨配合的自航问题中螺旋桨载荷径向与周向分布不均匀的问题,此体积力模型也可以进行有效处理,使用致动点的轴向当地速度Vx与周向当地速度Vθ依照下式计算叶元体的水动力,图1展示了叶元体水动力计算各相关物理量的矢量关系:

图1 叶素动量理论Fig.1 Blade element momentum theory
式中:a与b分别表示轴向诱导因子和切向诱导因子,表征螺旋桨引起的诱导速度与来流速度的比值;n为螺旋桨转速;r为叶元体径向位置,;Vx与Vθ分别表示当地轴向速度和当地切向速度,即螺旋桨扰动产生的诱导速度与来流速度的和;Va与Vt分别表示大地坐标系下的轴向来流速度和切向来流速度,表征无穷远处流体相对于叶元体的速度;β为进角;φ为叶元体螺距角;α为几何攻角,;CL与CD分别表示叶元体的升力系数和阻力系数;cr为对应径向位置处的叶元体弦长;dr为叶元体展向长度;dFL与dFD分别代表叶元体的升力和阻力。
1.3 叶元参数
叶元参数为叶元体升阻力系数与攻角的对应关系,在使用体积力模型前存储到特定文件中,并由体积力计算程序实时读取。本文通过对敞水试验CFD 模拟结果中的叶元壁面进行压力和粘性力积分,可以分别得到叶元体的升力和阻力系数,进而确定各叶元体升阻力系数与攻角的对应关系。在执行体积力程序时,叶元性能由分段线性插值得到对应攻角下叶元体的升阻力系数。具体的实施流程如下:首先进行螺旋桨敞水试验的CFD 数值模拟,并将螺旋桨壁面沿径向等距分为多个叶元,各叶元体对推力与扭矩的贡献dT与dQ通过表面压力积分得到(图2),进而计算叶元体的升阻力系数,并将所得力系数与攻角的对应关系保存为数据向量,由体积力计算程序通过分段线性插值方法读取。在体积力程序的执行过程中,首先通过诱导因子与当地速度得到叶元来流,进而计算叶元攻角α,最终通过攻角数据向量α与升阻力系数向量CL、CD经分段线性插值得到式(8)与式(9)中的升阻力系数。分段线性插值格式如式(10)、式(11)所示,此种插值方式可尽量减小数据处理造成的误差。

图2 螺旋桨叶元体Fig.2 Blade element of propeller
1.4 真实螺旋桨诱导因子分布
诱导因子体现了来流速度与当地速度的关系,如图3 所示。传统叶素动量理论中诱导因子的迭代求解基于理想流体理论[2,4],不适用于粘性求解器中的体积力模型,因此需要一种方法来研究粘性流场螺旋桨载荷作用下各叶元体来流与当地速度的关系。为得到这种关系,本文利用1.3节得到的叶元参数得到了多组来流速度下与真实螺旋桨模型载荷分布相符的体积力分布,并将此体积力分布作用于敞水流场中得到诱导速度场,如图4所示。在得到诱导速度场的过程中,叶元体的水动力大小不会随流场的变化而迭代。在此种情况下,最终得到的诱导速度场与真实螺旋桨的诱导速度场吻合程度较高。各叶元体的当地速度由计算稳定后的速度场在致动点位置处插值得到,并由同一径向位置处各致动点当地速度的平均结果代表此径向位置处的叶元体当地速度。最终由预设来流速度V与各径向位置处当地速度Vx计算各径向位置处的诱导因子大小。由于敞水试验中横向流动较弱,因此本研究中尚未考虑切向诱导因子。

图3 理想流体理论[2]Fig.3 Ideal fluid theory[2]

图4 基于真实螺旋桨载荷分布的诱导速度场Fig.4 Induced velocity field based on real propeller load distribution
经由上述过程,可以建立单个工况下诱导因子与径向位置的关系,也可建立同一径向位置处诱导因子与当地速度的关系。将各径向位置处诱导因子数据记为向量a,当地速度记为向量Vx并存储到特定文件中。在体积力模型计算过程中,通过插值得到致动点位置处的当地速度后,通过在此数据向量中进行分段线性插值可得到各径向位置处的诱导因子,如式(12)所示。由于建立了分段线性插值关系,在流场迭代求解中插值数据也将经过反复迭代,体积力模型能否通过迭代收敛到螺旋桨CFD数值模拟的载荷分布是本文提出的体积力模型是否具有应用性的关键。
2 算例设置
2.1 模型与工况
本文进行了KP505 螺旋桨真实模型及体积力模型的敞水试验数值模拟。图5 为KP505 螺旋桨几何模型。真实螺旋桨模型敞水试验转速为10 r/s,包含0.4、0.5、0.6、0.7、0.8 五个进速系数。拟合诱导因子的体积力模型工况参数与之相同。KP505螺旋桨主要尺度及拟合诱导因子工况参数如表1所示,体积力模型直径及毂径与之相同。

表1 KP505螺旋桨主要参数及敞水试验工况参数Tab.1 Main parameters of KP505 propeller and open-water test

图5 KP505螺旋桨Fig.5 Geometry of KP505 propeller
2.2 计算域及网格划分
图6为真实螺旋桨模型与体积力模型敞水试验模拟计算域大小。真实螺旋桨模型及体积力模型的计算域大小相同,均为圆柱形计算域,直径为5D,桨盘面至入口为3D、至出口为5D。图7 为螺旋桨敞水试验网格划分,真实螺旋桨模型算例网格量为251 万,时间步长取0.0005 s。体积力模型算例网格量为46 万,时间步长取0.001 s。真实螺旋桨模型采用滑移网格方法,滑移面附近及螺旋桨壁面均进行逐级加密。图7(b)中圆柱区域为体积力作用区域,径向网格数量为38 个,周向网格数量为104个。网格无关性验证与时间步长无关性验证已由之前相关工作完成[17]。

图6 KP505螺旋桨敞水试验模拟计算域Fig.6 Computational domain of KP505 propeller open-water test simulation

图7 KP505螺旋桨敞水试验模拟网格Fig.7 Grids of KP505 propeller open-water test simulation
3 结果分析
图8为改进的体积力模型与真实螺旋桨模型敞水曲线模拟结果,其中real、bf与exp分别代表真实螺旋桨模型和体积力模型的计算结果以及螺旋桨敞水性能的物理实验结果。可以发现三者有较好的吻合程度,表明真实螺旋桨的CFD具有准确性。同时表明在应用了符合真实螺旋桨模型的叶元性能与诱导因子分布后,在不使用翼型理论经验公式的情况下,体积力模型的准确度得到了有效提高。图9 展示了各进速条件下体积力模型相对于真实螺旋桨敞水曲线计算结果的误差,除J=0.4 时推力系数误差为1.05%外,各进速条件下推力系数误差与扭矩系数误差均在1%以内,其中扭矩系数误差均在0.8%以内,且误差水平未随进速系数出现较大变化,表明改进后的体积力模型误差水平不再与进速系数敏感[4,7,11],其准确性可适用于不同工况。两种模型模拟条件下桨载荷在其中三种进速条件下的径向分布如图10 所示。其中axial 与tangential 分别代表轴向载荷与切向载荷,并进行了无因次化处理。两种模型数据的吻合程度较高,表明改进后的叶素动量理论模型可以通过不同径向位置处的当地速度得到符合真实螺旋桨载荷分布的叶元水动力稳定值。
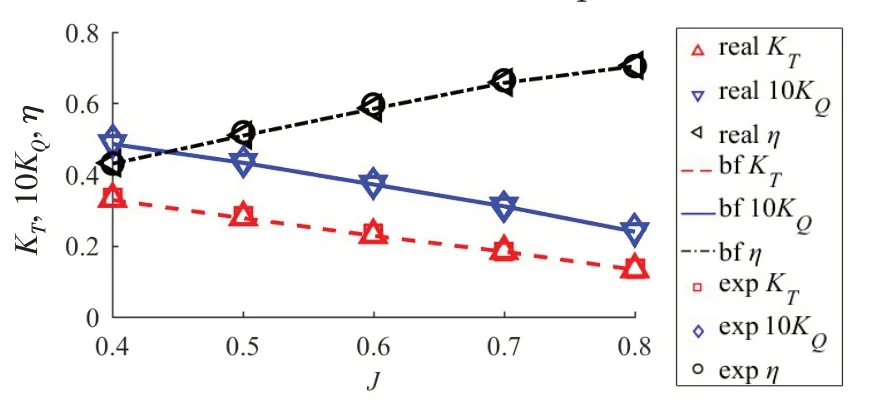
图8 敞水曲线模拟结果Fig.8 Open-water-curve simulation results
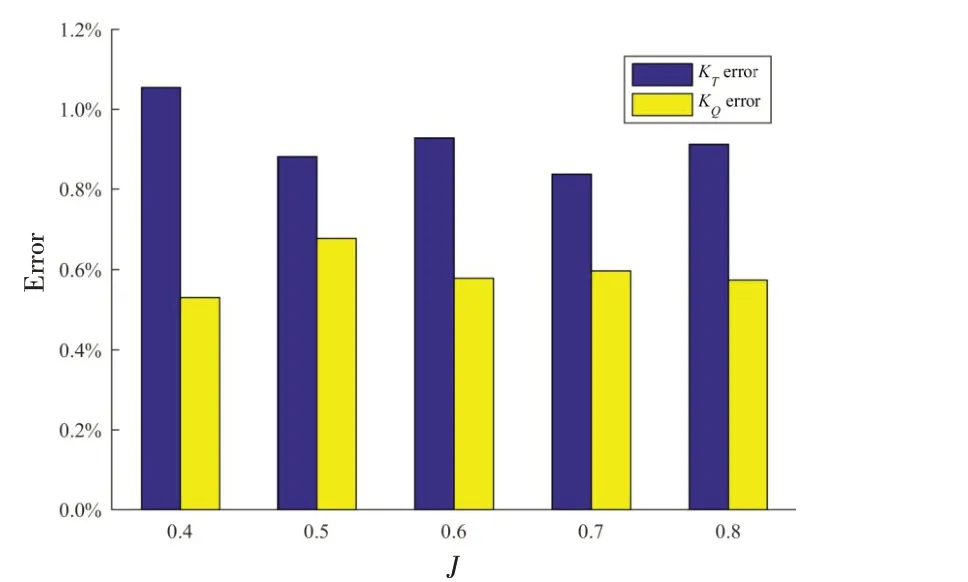
图9 体积力模型敞水曲线误差分布Fig.9 Error distribution of open-water-curve of body-force model

图10 螺旋桨载荷分布模拟结果Fig.10 Simulation results of propeller load distribution
图11 与图12 分别为J=0.5 与J=0.7 条件下两种模型的尾流场轴向速度对比,其中图12 为桨盘面后0.5D、1D与1.5D处的位置数据,此分布范围囊括了一般桨舵干扰工况下舵模型的位置[17]。真实螺旋桨模型的尾流场数据为一个旋转周期内的时均数据。诱导速度峰值分布在0.6R~0.8R范围内,与图10中最大桨载荷位置相同。可以发现诱导速度分布峰值附近的较大范围内两种模型的速度分布在两种工况下的吻合程度均较高,表明体积力模型可以模拟真实螺旋桨尾流不同截面中的动量输运。在轮毂处两组数据存在一定差距的原因为在进行体积力模型模拟时未考虑桨轴及轮毂壁面的建模,因此忽略了真实螺旋桨模型桨轴与轮毂的阻塞效应,导致体积力模型诱导速度场轮毂附近速度偏高。此差异随流场的向后发展逐渐变小,且对于螺旋桨尾流动量输运不起主要影响作用。同时从图10中可以发现,桨毂附近的叶元体载荷为整个桨叶中的最低水平,对螺旋桨性能不起主要作用,因此桨毂存在对螺旋桨性能的影响可以忽略。两种模型尾流分布存在细微差异的另一原因是真实螺旋桨壁面的扰动作用产生了大量复杂涡结构,而体积力模型由于忽略了叶片旋转效应,涡结构更加平滑有序。图13为两种模型计算得到的涡结构(Q=50等值面)对比。体积力模型无法还原较为精细的流场信息,但可以通过替代真实螺旋桨模型有效减少螺旋桨尾流动量输运模拟的计算成本。

图11 尾流场模拟结果Fig.11 Simulation results of wake flow field

图13 体积力模型与真实螺旋桨模型的涡结构Fig.13 Vortex structure of body-force model and real propeller model
4 结 语
本文通过拟合诱导因子的方式,将诱导因子与当地速度的对应数据存储到叶素动量理论的执行过程中,使用螺旋桨敞水CFD数值模拟计算叶元性能,并将改进后的体积力模型应用于五组进速下的KP505螺旋桨敞水试验数值模拟。基于改进叶素动量理论体积力模型模拟的KP505螺旋桨敞水试验结果表明,体积力模型可以从初始流场迭代到螺旋桨CFD 数值模拟的工作状态,其螺旋桨性能、载荷分布以及尾流分布均与螺旋桨直接数值模拟的结果相近,且不同进速下均有较好的预报精度,敞水误差在五种进速下均未超过1.2%。
以上研究表明,基于符合真实螺旋桨诱导因子分布改进后的叶素动量理论模型,适用于不同进速下的螺旋桨敞水性能预报,克服了以往叶素动量理论体积力模型的准确性随模拟工况变化敏感度高的问题。在不均匀来流问题如船桨干扰问题中,桨盘面各处的来流速度不同,特别是在船舶操纵条件下螺旋桨的入流条件更加复杂,因此在较大进速范围内保证叶素动量理论体积力模型的计算准确性对于解决此类问题具有较大的意义。本文提出的改进体积力模型预报得到的螺旋桨的诱导速度场与真实螺旋桨吻合程度较好,因此可以较为准确地代替真实螺旋桨进行桨与其他结构物的相互作用模拟,在降低计算时间与存储空间需求基础上还能较好地提升计算精度,为未来船桨舵干扰下的水动力性能高效评估提供了必要的技术支撑。
