例析导数中隐零点问题的解题技巧

黄卫民

江西省临川第二中学 (344100)

在求解函数问题时,很多时候都需要求函数f(x)在区间I上的零点,但所述情形都难以求出其准确值,导致解题过程无法继续进行时,可这样尝试求解:先证明函数f(x)在区间I上存在唯一的零点,这时可设出其零点是x0,因为x0不易求出(当然,有时是可以求出但无需求出),所以把零点x0叫做隐零点.

实际上很多隐零点问题产生的原因就是含有指对项,而这类问题又往往具有同构特征.一般地,隐零点代换需要同构才能求解．否则,我们可能很难找到隐零点合适的代换化简方向．例如,常用的隐零点的同构:

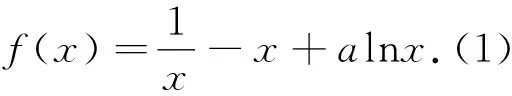
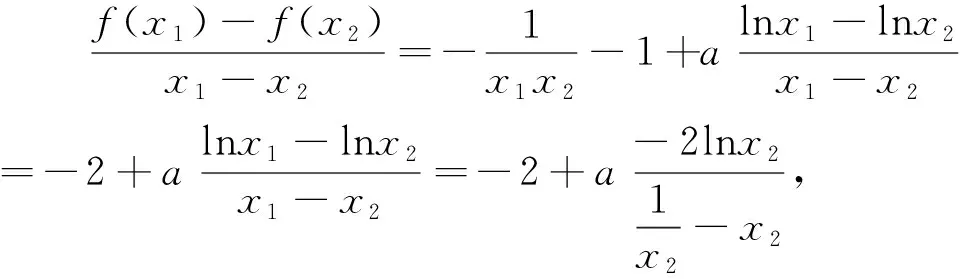
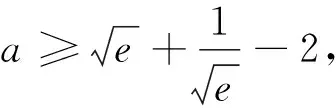
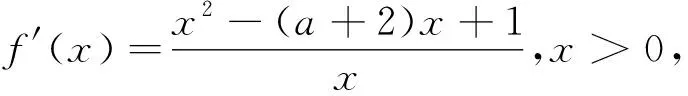
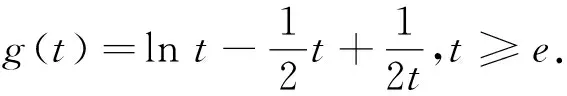
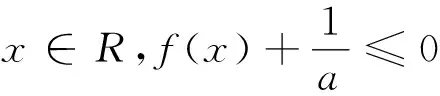
解析：f′(x)=4ae2x-(x+1)ex=

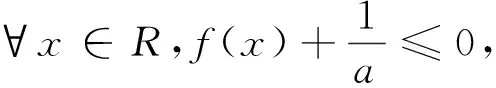
变式已知函数f(x)=ln(ax),a>0,若f(x)≤(x-1)ex-a, 求a的取值范围.

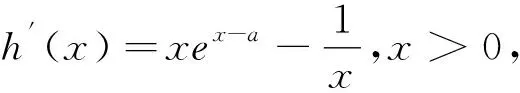
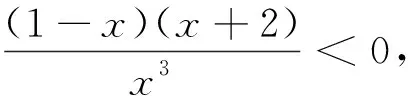
由上述实例可见,求解导数中二次函数或非二次函数的隐零点问题是常见的处理方法,而隐零点问题是高考导数压轴题最常考的类型之一,其中虚设零点法则是其中难度较大、出现较频繁的题型,它能综合考查学生对导数掌握的熟练程度,学生应在理解透“虚设零点”的基础上多加练习以期熟能生巧．