一道三角模考题的多角度分析

董慧敏 王洪军

内蒙古师范大学附属中学 (010020) 内蒙古呼和浩特市托克托县第一中学 (010200)

解三角形是高中数学中的核心内容之一,尽管在高考中占有很大的比重,但试题难度适中,因此它成为学生在考试中的主要得分部分.本文以高三模拟考试中一道与角平分线有关的解三角形题为例进行多角度分析.

典例在ΔABC中,∠BAC的角平分线AD与边BC交于D点,求证:AD2=AB·AC-BD·DC.

本题的一般做法是分别在ΔABD和ΔACD中利用余弦定理,借助“爪型结构”进行分析证明.

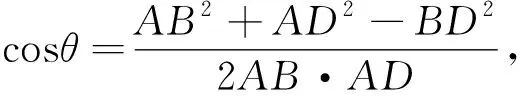
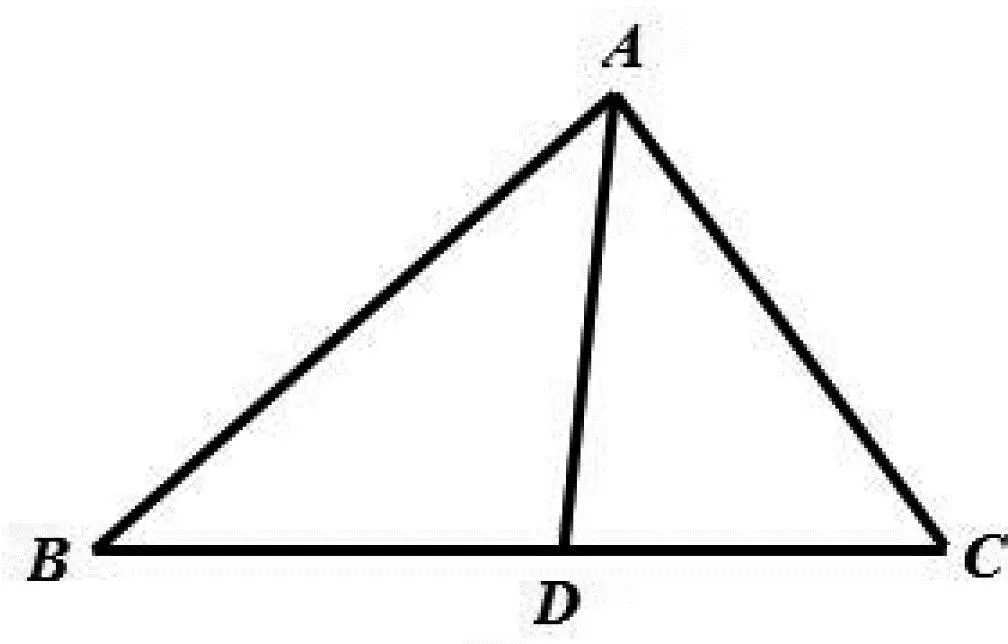
图1

从上述证明过程能够看到,利用余弦定理建立等式之后,所得到的等式与待证式之间没有特别明显的联系,对学生来说变形整理的方向并不明确,思维量较大,让学生望而却步.鉴于日常教学过程中对于角分线的问题,笔者有意识的强化了借助面积之间的关系建立表达式的这种想法,由此可以得到如下证明.

证明2：如图1,令∠BAD=∠CAD=θ,在ΔABC中,由余弦定理可得cos2θ=

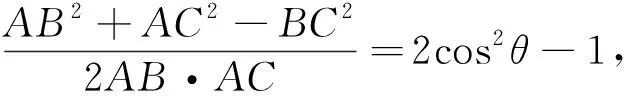
上述证明最直接的感受就是过程较为繁杂,相对来说,变形整理时的方向明确些,实际教学过程中学生对这一证明方法较为认可,能达到这种效果的前提是前期的教学过程要有意识的渗透某种思想、某些解题理念以及相关数学知识等.

我们知道,在学习数学的过程中如果直接论证方向不明,产生思维障碍时,不妨从结论出发,执果索因,探寻解决问题的方法,因此下面的证明是讲解过程中思路最清晰的.

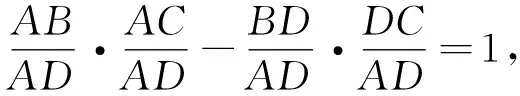
典例中所得结论其实是平面几何学中以荷兰数学家斯库顿(Schouten,1615—1660)的名字来命名的定理,它在解题中有着广泛的应用,下面通过两个具体例题进行说明.

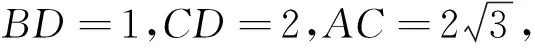
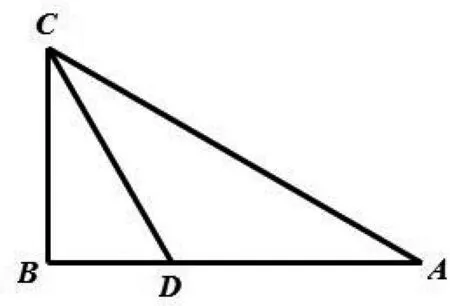
图2

从上面的解答过程可以看到,利用斯库顿定理可以比较方便的建立与角平分线有关的等式,简化运算也降低了思维量,我们还可以通过下面解析几何的题目进一步体会其作用.

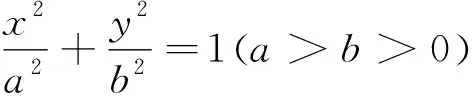
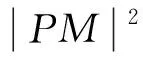
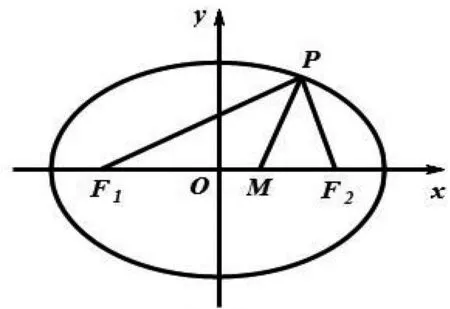
图3

|PF2|-|F1M|·

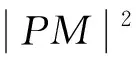
需要说明的是,斯库顿定理的逆定理也是成立的,实质上它与三角形内角平分线定理是等价的,它还能推导平面几何中的其他定理或结论,这里就不在一一阐述了,有兴趣的读者可以自行研究.

数学教育家波利亚说过“掌握数学意味着善于解题”,解题教学在中学数学教学中占据重要地位,解题教学不仅仅是要教会学生怎样解题,更重要的是要教会学生如何思考,尤其是遇到学生普遍有问题的题目,更要弄清楚学生产生思维障碍的根源.笔者在教学过程中尽量找到这类问题的“题根”,也就是以本质相同但相对来说更为简单的题目为出发点,通过变式逐步将其转化为学生有疑问的题目上,将未知的复杂问题与熟悉的简单问题建立联系,避免套路化的总结方法,让学生在思考问题的过程中自己感受方法的通用性与特殊性,尽量做到化“冰冷的美丽”为“火热的思考”.解题有法,但无定法,不明原因的机械套用,不利于数学思维的培养与能力的提升,也与现行的课标要求不符.