一道不等式问题的解法溯源及推广
2024-01-19袁丁
中学数学研究(江西) 2024年2期
袁 丁
安徽省蒙城县第二中学 (233500)
问题1 (《数学通讯》2023年第3期问题征解第600题)已知正数a,b,c满足a+b+c=3,求证:
看到此题,容易联想到“2011年克罗地亚数学奥林匹克试题”:
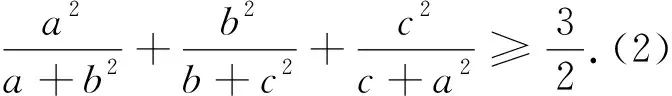
对于不等式(2),较为常见的是下面这种简单的证法.
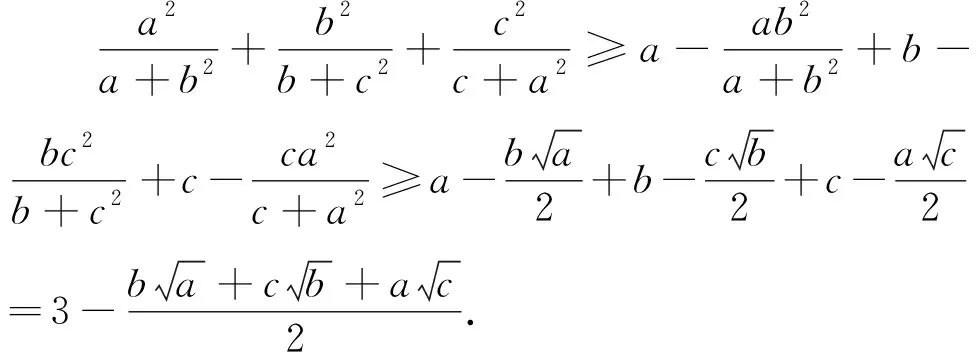
经过探究发现,证法1对于(1)式的证明却显得无能为力.但是,从不等式(1)和不等式(2)的结构上看,都是同一类型的轮换对称的非齐次不等式,由此猜想问题2一定有某种证法可以传承到问题1,带着这样的思考,经过对(2)式结构的再次分析,获得如下两种证法.
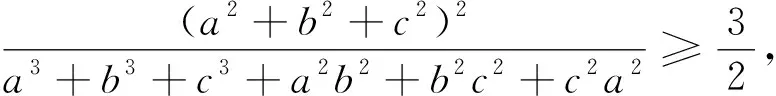
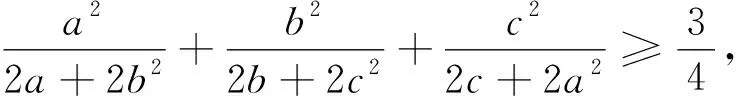
点评:证法2和证法3,入手的角度稍有不同,后者看似“多此一举”了一步,但是后面的处理却比前者要方便、容易得多,而且用证法3证明(1)式则十分顺畅.
一直到四月一日,孙山才来电话,说:“小说家这样写,S决定先离开果城,得摆脱一切可能的盯梢者,吃过大亏了,不能重蹈覆辙。他找了一个清静之所,闭关修炼——在云南香格里拉的建唐镇隐居,那时还不叫香格里拉,叫中甸。他购买了十几本如何成为一位私家侦探的书籍,潜心研读,甚至旁涉了法学、心理学、刑侦学等相关学科,对擒拿格斗及枪械也略有兴趣,还去散打俱乐部训练了三个月。一年多之后,他自信远非吴下阿蒙,萌生了开一家私家侦探社的想法。那个年月,以抓小三、讨欠薪、刺探商业机密等为主要业务的私家侦探社游走于灰色地带,在大城市像雨后春笋冒出来——”
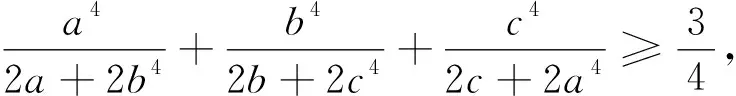
问题1和问题2中每个分式的分子与分母中不同变量的指数分别是2与4,都是偶数,如果是奇数比如3,上述证法还能用吗?答案是肯定的.
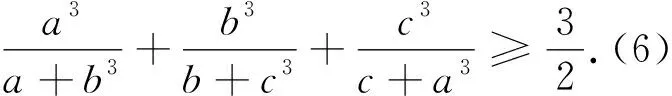
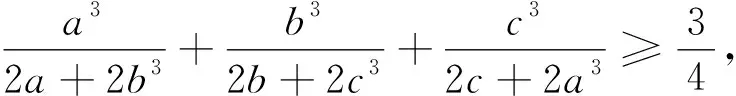
由柯西不等式知可转化为
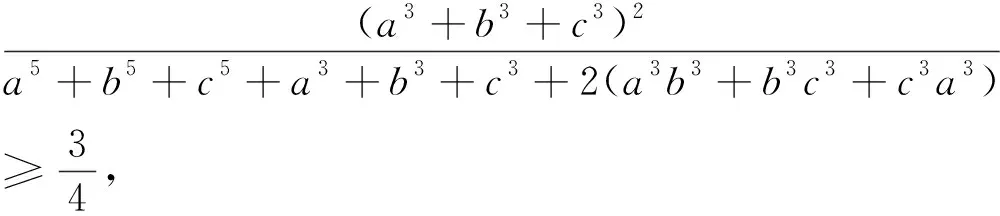
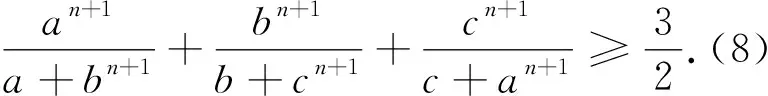
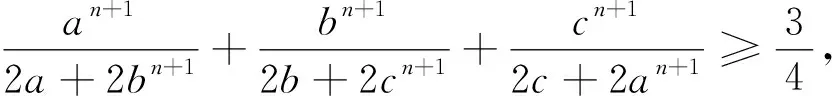
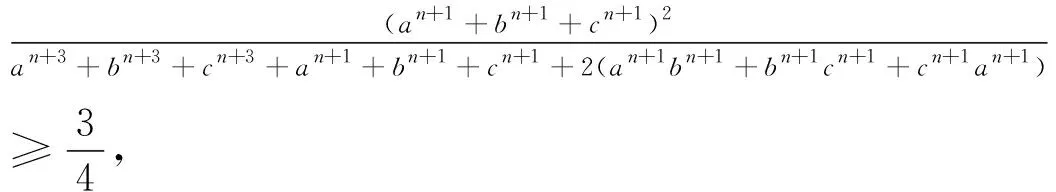
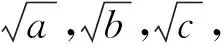
推广已知正数a,b,c满足a+b+c=3,n∈N+,求证:
