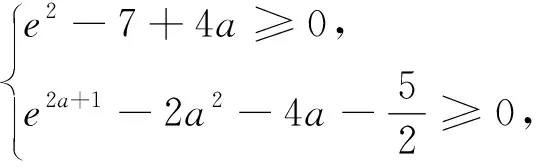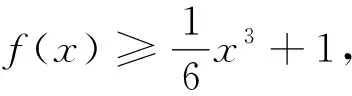端点效应不灵了?
2024-01-19黄永生纪建灵
黄永生 纪建灵
福建省泉州市第七中学 (362000);福建师范大学泉州附属中学 (362000)
2020年全国一卷理科21题第(2)小题为不等式恒成立求参数范围问题,具有高度的迷惑性,考生解题时很容易陷入“端点效应”的误区.本文从“端点效应”典例出发,探究误用“端点效应”产生错解的根本原因,并提出“端点效应”模型的四种判断策略,从而提升解题效率.
1 端点效应及应用典例
定义在[a,+∞)上的函数f(x),若满足f(a)=0,f′(a)=f″(a)=…=f(n-1)(a)=0,f(n)(a)≥0且f(n)(x)单调递增,则f(x)≥0在[a,+∞)恒成立.
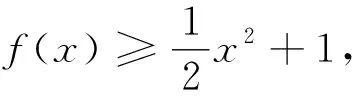
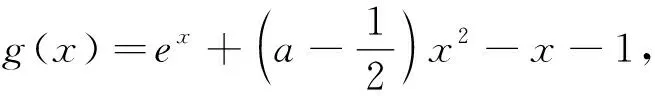
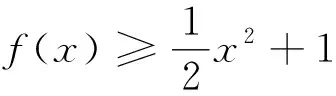
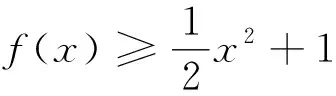
(2)当g″(0)=2a<0,即a<0时,由g″(x)=ex+2a-1=0得x=ln(1-2a).
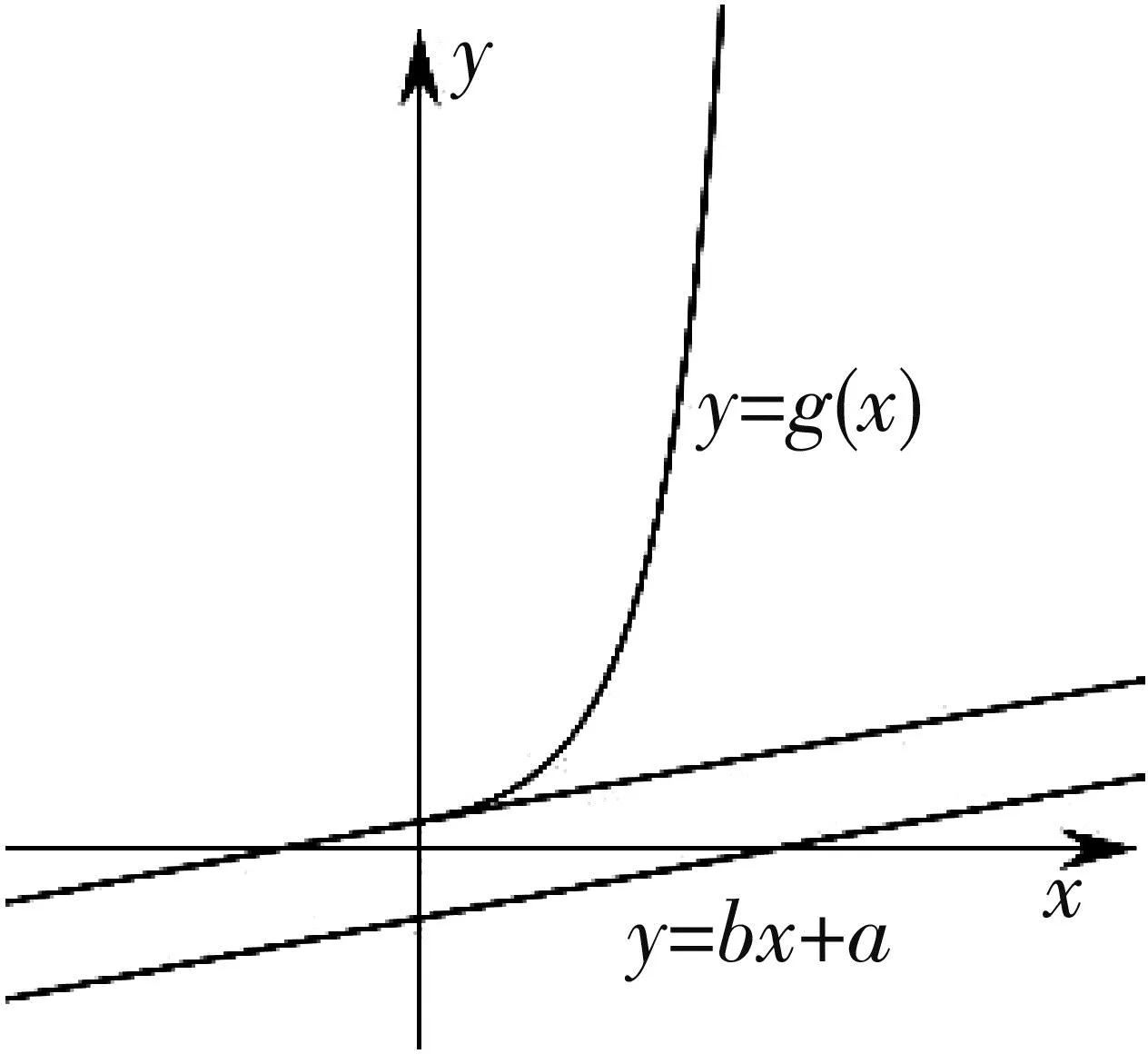
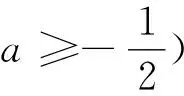
当x∈(0,ln(1-2a))时,g″(x)<0,g'(x)单调递减.所以g'(x) 综上,a≥0. 评析:端点效应试题的结构为“若x∈[a,+∞),f(x,m)≥0,求m的取值范围”,其解题思路为:①观察得f(a)=0,由f'(a)≥0得到一个必要条件;若f'(a)=0恒成立,则由f″(a)≥0得到必要一个条件;若f″(a)=0恒成立,则重复以上步骤,得到m∈P.②证明m∈P,f(x,m)≥0成立;③当m∉P时,找到区间,证明f(x,m)<0. 图1 策略1f(n)(x)的正负性与单调性 定义在[a,+∞)上的函数f(x),若满足f(a)=0,f'(a)=f″(a)=…=f(n-1)(a)=0,f(n)(a)≥0且f(n)(x)单调递增,则f(x)≥0在[a,+∞)上恒成立. 策略2泰勒展开式 策略3数形结合 设g(x)为下凸函数,不等式g(x)≥bx+a对于任意x∈(0,+∞)恒成立.即要找到最佳系数a,b使直线y=bx+a恒在曲线y=g(x)的下方.考虑直线y=bx+a与曲线y=g(x)相切为临界状态.直观发现:如图2,当切点在端点,即b=g'(0),则a≤g(0);如图3,当切点不在端点,即b>g'(0),则a≤t.(t为相切时切线在y轴的截距) 图2 图3 显然,图2为端点效应问题,图3为非端点效应问题. 图4 策略4寻找最值点 基于策略3的讨论,例2可改编为以下试题,有兴趣的读者不妨运用以上策略判断是否为端点效应问题,再作解答. 试题1 已知函数f(x)=ex+ax2-x.当x≥0时,f(x)≥(3-e)x3+1,求a的取值范围. (答案:a≥5-2e) 试题3 已知函数f(x)=ex+sinx,当x≥0时,f(x)≥ax2+2x+1,求a的取值范围.2 误用端点效应及错因分析

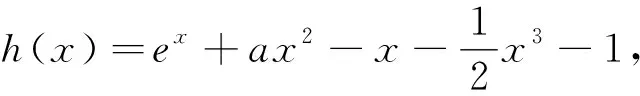

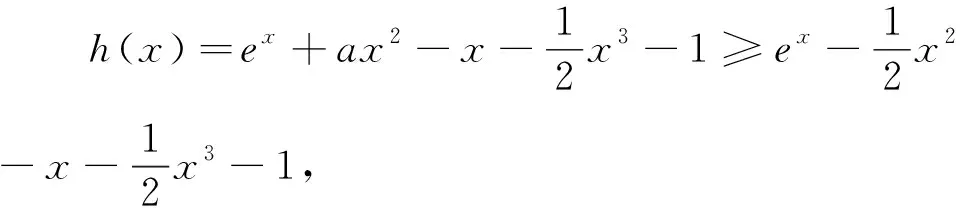

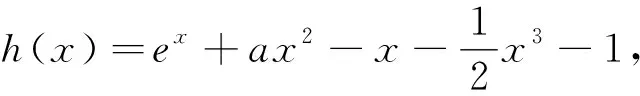
3 端点效应的判断策略