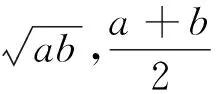教学,多一些贴合——以“基本不等式证明”教学为例

潘龙生

江苏省盐城市第一中学 (224005)

教之道在于度,对于这个度,笔者给出了这样一种诠释:贴合就是度.教学,就是要多一些贴合,即贴合教材意图,贴合学生实际,贴合教学发展.近期,笔者作为评委参与了某市高中数学优质课评选活动,课题是《基本不等式的证明》(苏教版普通高中课程标准实验教科书必修5第三章《不等式》的第4讲第一课时),最后应邀就本课题上了一节示范课,现将这节课的教学过程实录如下,并就这三层贴合谈一些感受和体会,期与同仁们探讨.

1 创设情境 提出问题

师:我这有一张A4纸,大家知道A4纸(矩形)的长、宽分别是多少吗?我来告诉大家,长29.7厘米,宽21厘米.

现在我们就从这张A4纸开始本节课的学习.

师:矩形变正方形.

正方形1:面积相等;正方形2:周长相等.

思考:两个正方形的边长谁大?

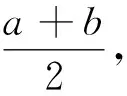
这就是本节课我们一起要探究解决的问题——《基本不等式的证明》.

2 引导探究 解决问题

生2:作差比较:(展台投影)

证法1：

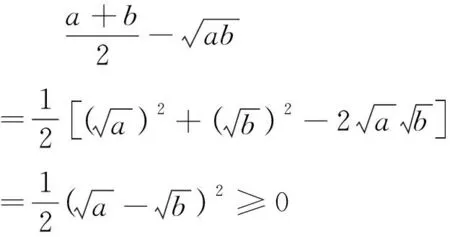
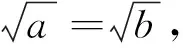
师:很好,比较两个量的大小,我们可以转化为比较两个量的差与0的大小(板书:①比较法).

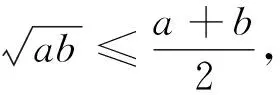
师:再看下一位同学的证明:

证法2：

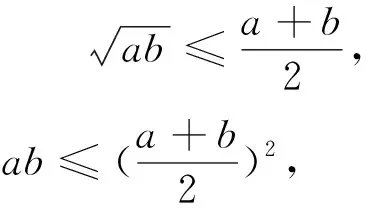
4ab≤a2+2ab+b2,

0≤(a-b)2

师:谁来点评下这种证法.

生4:这种证法不对,把证明的结论当条件用了.

师:从这位同学的证明过程中可以感受到解题的思路,这么修改一下就对了.

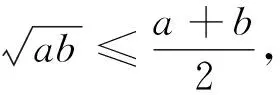
只要证4ab≤a2+2ab+b2,

只要证0≤(a-b)2

师:这个证法叫做分析法,最明显的特点是从结论出发,推出一个已有的结论,用四个字概括为“执果索因”.(板书:②分析法)

师:如果不想采用分析法这样的证明格式,也可以根据分析法的思路,从不等式成立需要的条件逐步推导到要证明的结果,这种方法叫做综合法,也可以用四个字概括为“由因导果”.(板书:③综合法)

对于正数a,b,有(事先手写好,直接投影):

0≤(a-b)2,

3 探幽入微 加深理解

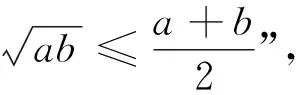
下面再来欣赏一下这个发现,请问其成立的前提条件是什么?

生5:a>0,b>0.

师:能不能将这个条件扩大到更大的范围?

生5:如果a,b中有一个或者两个都为0,也是可以的,但不能是负数,可以推广到a≥0,b≥0.

师:很好,基本不等式描述了两个正数的几何平均数不大于它们的算术平均数,还可以用其它方式描述吗?(学生思考,画外提示音)

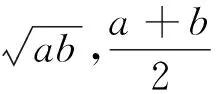
(此处停顿1～2分钟,巡视学生思考情况,机动处理)

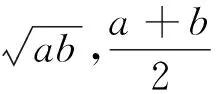
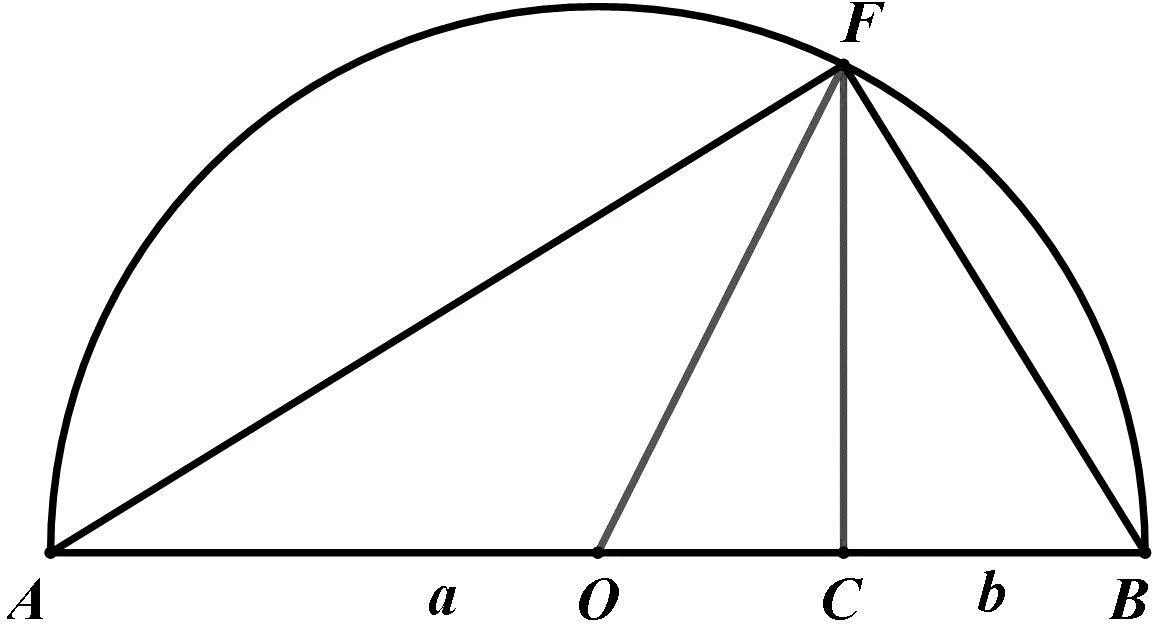
图1

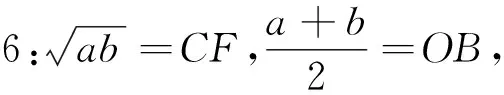
师:很好,这就是基本不等式的几何解释.

师:图形构造简洁直观,堪称基本不等式美妙的无字证明.有人说,图形是一种语言,在这里,它是一首无字的诗.下面我们再来欣赏一首诗.

(观看微视频:《基本不等式几何证明赏析》)

师:赵爽弦图中所蕴含的不等关系a2+b2≥2ab,何时取等号?成立的条件又是什么?

生7:a=b时取“=”,不等式成立的条件为a>0,b>0.

师:能进行推广吗?

生7续答:可以推广到a,b为一切实数,因为(a-b)2≥0恒成立.

师:得到的这些不等式为基本不等式的变式.a2+b2≥2ab和基本不等式或其变式之间有关联吗?

师:这可以证明不等式a2+b2≥2ab,大家再从结构上观察它们之间的相通之处.

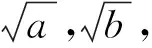
师:正确,a2+b2≥2ab也是基本不等式的一种变式,至于其它的变式,留给同学们课后去探究.

4 学以致用 巩固成果

例设a,b为正数,证明下列不等式成立:

(巡视学生证明情况,寻找典型案例,案例一学生采用比较法证明,案例二学生采用刚刚学习的基本不等式证明,请学生点评)

生12:这两种证明方法都可以,但既然我们已经学习了基本不等式,直接使用其结论进行证明更简洁.

师总结:对于满足基本不等式结构特征的式子可以直接使用基本不等式来证明.

(学生自主训练,合作批改讨论,教师总结点评)

师:利用基本不等式进行证明时,当问题不满足定值条件或同正条件时,可以通过构造来实现.

5 课堂小结 盘点收获

数学知识:①成立条件a≥0,b≥0;②描述方式:几何平均数不小于算术平均数;半弦不大于半径.③应用类型:证明不等式.

数学方法:①归纳猜想;②数形结合;③特殊一般.

6 教学 多一些贴合

6.1 贴合教材意图,定位合理教学内容

教学不能唯教材论是目前一致的共识,不唯教材指的是教学不能按部就班、一成不变地套用教材,而应该对教材的内容进行适当整合,调整最佳教学顺序,但无论怎么调整,合理定位教学内容,贴合教材意图这是基本要求.从对课标和教材的理解上,《基本不等式的证明》应该包含两层教学含义,即基本不等式本身的被证明和运用基本不等式证明其他不等式.审视参评的教学设计,不少教师淡化了这两类证明,而基本不等式的应用,如求函数的最值或实际问题中的应用,则占了课堂教学的很大篇幅,这明显偏离了教学重心,越过了本课合理的教学范围.对于这个问题,笔者在教学前与苏教版教材的主要编写者作了交流,得到了肯定,在教学中作了较为准确的定位,同时也得到了与会教师的一致认可.

6.2 贴合学生实际,创设合适问题情境

创设合适的问题情境可以激发学生的学习兴趣和动机,从而调动学生的学习积极性和主动性,但情境的创设要贴合学生实际,如果为了“情境”而凭空创设一些脱离学生认知实际的情境,则不能引起学生共鸣与互动.针对参赛选手的各种情境设计,笔者做了如下思考:按教材以物理中的天平称重引入两个均值再去比较大小,天平在生活中运用很少,只是在物理实验中使用,学生难以产生一致共鸣,且模型不是太简单,仅为了引出这两个均值,稍显不“经济”;以24届国际数学家大会会标引入,也就是借助赵爽弦图得到基本不等式的一个变式,高一学生对图形的阅读分析能力还有欠缺,作为引入,应该简洁,直白些;以基本不等式的几何意义引入,图形中由半弦和半径的不等关系直接得到均值不等式,但是后继的探究、归纳猜想就不能展开,不便于在数学教学中培养学生分析解决问题的能力.基于这些思考,笔者以学生熟悉的A4纸为背景设计了一个简单的数学问题,引出算术平均数和几何平均数的定义,由于贴合学生的实际认知,这个设计也激发了学生对两个平均数不等关系的思考,从而顺利地引出本节课的课题.

6.3 贴合教学发展,调整合时呈现方式