基于波形距离系数的逆变站近区交流线路保护方向元件

冀肖彤，柳 丹，熊 平，陈 玉，杨 霖，文明浩

（1.国网湖北省电力有限公司，湖北省武汉市 430077；2.国网湖北省电力有限公司电力科学研究院，湖北省武汉市 430077；3.华中科技大学电气与电子工程学院，湖北省武汉市 430074）

0 引言

高压直流输电技术不断发展，电压等级、输送容量不断提升，在远距离大容量输电、新能源并网、非同步交流系统互联等场景下发挥了极为重要的作用［1-4］。目前，中国已经形成了世界上电压等级最高、规模最大的交直流混联系统。如何有效保证交直流混联系统的安全稳定运行，是亟待突破的难题［5-8］。

当逆变站近区交流线路发生故障时，交流电压出现跌落，可能引起逆变站发生换相失败，导致逆变站的输出产生畸变［9-11］，将对继电保护动作性能产生不利影响。方向元件是距离保护的重要组成部分，准确地识别故障方向是距离保护近区故障可靠动作的前提。然而，当线路出口附近发生金属性短路故障时，保护安装处的测量电压很低，故障方向识别难度大，若不能及时判断故障方向、切除故障，可能会造成换流站设备的损坏，危及电力系统的安全稳定运行。

在传统交流系统中，工频变化量方向元件以其原理简单、不受负荷特性和系统振荡影响的优势得到了广泛的应用［12］。同时，工频变化量方向元件在出口近区故障工况下仍具有很高的可靠性和灵敏度。在对逆变站近区的交流线路的故障方向判别原理研究中，工频变化量方向元件同样受到了大量研究的关注。文献［13］给出了直流系统的工频变化量等值模型，并指出逆变站仅有单回出线运行时，工频变化量方向元件将无法正确动作。文献［14-15］分析了直流接入对交流保护的影响。文献［16］提出了逆变站近区交流线路高阻接地故障保护方法。文献［17］对逆变站单回交流出线时，交直流混联系统故障后的暂态功率倒向问题进行了分析，指出工频变化量方向元件在系统发生功率倒向时可能发生误动。文献［18］分析了逆变站单回和多回交流出线下工频变化量方向元件的适用性，并指出逆变站交流出线为单回线的情况下，工频变化量方向元件不再适用。

针对逆变站近区交流线路方向元件的适应性问题，部分研究从改进信号提取算法、聚焦暂态分量、提取直流系统故障特征量等多种角度入手，对工频变化量方向元件进行改造，同时也提出了适用于逆变站邻近区域交流线路的方向元件。文献［19］采用最小二乘法识别线路零模参数，实现逆变站交流出线的故障方向判别，不过该方法仅适用于接地故障。文献［20］利用同步挤压小波变换提取故障暂态特征，采用高频暂态能量构造故障方向识别判据，然而如何有效抑制噪声干扰仍有待研究。基于时域波形相似度的保护算法研究近年来受到广泛关注，文献［21］提出了一种基于电压相关系数和低电压识别判据的出口故障方向判别方案，并对其性能进行了分析，不过该方法中波形相关系数门槛值的整定有待进一步研究。文献［22］提出了基于余弦相似度的交流线路快速纵联保护，不过该算法仅适用于传统交流线路，并不适用于高压直流输电系统逆变站送出线路。文献［23］基于改进的Hausdorff 距离算法，提出了多端直流输电线路纵联保护方案。综上，现有研究表明，高压直流换流站会对传统方向元件性能产生不利影响，尤其是逆变站仅有单回出线时，如何快速判别逆变站近区故障方向仍面临较大困难。本文利用逆变站交流母线边界元件实现故障方向判别，不同故障类型和不同故障时刻均能快速可靠判断故障方向，同时具有一定的抗噪声能力。

本文对逆变站邻近区域交流线路出口故障的方向判别开展研究，利用逆变站近区设备的故障电流特征，提出了基于波形距离系数的出口故障方向判别原理。基于PSCAD/EMTDC 电磁暂态建模，对所提出的故障方向判别原理进行了仿真验证。结果表明，所提出的方向元件能够可靠识别保护出口近区金属性故障方向，具有较高的可靠性和灵敏度。

1 逆变站近区线路出口故障特性分析

典型的交直流混联系统模型见附录A 图A1，交流系统1 为送端，经换流站和直流线路将功率输送至受端交流系统2，其中，逆变站出口经单回出线连接至交流系统2。换流站的结构如附录A 图A2 所示，两个6 脉动换流器在直流侧串联，在交流侧分别经星形/星形换流变压器和星形/三角形换流变压器并联至换流母线。两侧换流母线接有交流滤波器和无功补偿装置，其结构和参数如附录A 图A3 所示。为了表述方便，下文将交流滤波器和无功补偿装置统一称为交流边界元件。

1.1 故障电流特性分析

逆变站邻近区域交流线路出口故障位置如图1所示。发生正向出口故障（F1）时，根据基尔霍夫电流定律（Kirchhoff’s Current Law，KCL），交流线路保护装置测量电流为：

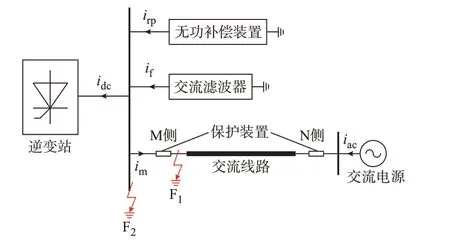
图1 逆变站近区交流线路故障位置示意图Fig.1 Schematic diagram of outgoing AC line fault near inverter station

式中：im为线路测量电流；idc为逆变站注入交流系统的电流；ib为交流边界元件向故障点注入的电流，如图1 所示，ib由irp和if两部分组成，其中，irp为无功补偿装置的注入电流，if为交流滤波器的注入电流。

发生反向出口故障（F2）时，根据KCL，忽略线路电容的影响，线路测量电流为：

式中：iac为图1 中交流电源向故障点注入的电流。

可以看出，逆变站近区线路发生出口故障时，正向故障和反向故障下，提供故障电流的电源存在显著差异。正向故障下的故障电流中将包含交流边界元件提供的电流成分，反向故障时则不包含。因此，正向故障时，线路测量电流im与交流边界元件电流ib将呈现出较强的相似性；反向故障时，线路测量电流im与交流边界元件电流ib无关。故可以通过比较线路测量电流im与交流边界元件电流ib之间的相似特征判别故障方向。

由式（1）可知，正向故障时，线路测量电流中包含交流边界元件输出电流ib和逆变站输出电流idc两部分。逆变站电流将对线路测量电流和交流边界元件电流的相似程度产生影响。

为了减小逆变站稳态输出电流的影响，定义电流时域变化量Δiφ(t)。iφ(t)为t时刻φ相电流的瞬时值；Δiφ(t)为t时刻电流iφ(t)的瞬时值与1 个工频周期T前该电流瞬时值iφ(t-T)的差值，即：

联立式（1）和式（3）可得，正向故障时，线路测量电流的时域变化量Δim(t)为：

式中：Δim(t)为t时刻的线路测量电流变化量；Δib(t)为t时刻的交流边界元件电流变化量；Δidc(t)为t时刻的逆变站注入交流系统电流变化量。

反向故障时，线路测量电流的时域变化量Δim(t)为：

式中：Δiac(t)为t时刻的交流电源向故障点注入电流的变化量。

对比式（4）和式（5）可以看出，正向故障和反向故障下的线路测量电流变化量Δim(t)与交流边界元件电流变化量Δib(t)的相似程度存在较大的差异。正向故障时，Δim(t)与Δib(t)存在较强相关性；反向故障时，Δim(t)与Δib(t)无关。

虽然引入电流时域变化量可以克服逆变站稳态输出电流的影响，但是由式（4）可知，逆变站输出电流变化量Δidc(t)仍然会影响Δim(t)与Δib(t)之间的相似程度。Δidc(t)越小，不同方向故障下Δim(t)与Δib(t)的相似程度相差越大。因此，需要分析逆变站输出电流时域变化量的特性。

1.2 逆变站电流时域变化量特性分析

受直流控制系统的延时和换相过程本身的时间影响，故障后的短时间内，逆变站提供的电流与故障前相比变化有限。对于12 脉动换流器而言，两次换相之间的时间间隔是1.67 ms（30°），若仅考虑故障发生到故障后的首个换相过程结束的这段时间，则逆变站提供的故障电流变化将来自两个方面：一是故障后直流电流的变化；二是若首个换相过程发生换相失败，晶闸管导通状态发生变化产生的电流变化。

对于故障后直流电流的变化，已有相关研究进行了说明。一方面，直流线路一般较长，逆变侧故障传导到整流侧需要一定的时间，两侧的直流电压差将导致直流电压出现上升；另一方面，受直流系统平波电抗器影响，直流电流的上升速度不会很快，因此，故障后短时间内直流电流变化幅度并不大，而且这种变化对于交流侧的故障类型和故障时刻并不敏感。可以认为在故障初期，直流电流的变化幅度不大［24-26］。

对于故障后首个换相过程发生换相失败的情况，由于组成12 脉动换流器的两个6 脉动换流器本身并无差异，只是相位上有所不同。因此，在故障发生后较短时间内，两个桥并不会同时发生换相失败，至多会出现其中一个桥换相失败。下面将分别进行分析。

1.2.1 故障后1 ms 未引发换相失败

若故障未引发换相失败，则此时逆变站电流的时域变化量仅受直流电流的变化影响，前面的分析指出，此时直流电流变化小。因此，相应的逆变站电流时域变化量Δidc(t)也较小。故可以认为在故障后1 ms 内，Δidc(t)近似为0。

1.2.2 故障后1 ms 引发换相失败

若故障引发了换相失败，那么交流线路故障后晶闸管的导通顺序会发生变化。此时，逆变站电流的时域变化量相对较大。

首先对换相失败的过程进行分析，以晶闸管V1→晶闸管V5换相过程中发生A 相接地故障为例，考虑故障刚好发生在换相过程中，V1→V5换相过程的等值电路如附录A 图A4 所示。此时，C 相不参与换相，A、B 相参与换相。若换相过程中恰好发生了A 相接地故障，则换相电压发生变化，如附录A 图A5 所示。附录A 图A6 展示了正常运行和换相失败时流经V1、V5的电流。

综上，换相失败发生后，逆变站电流变化量最大不超过直流电流幅值id。在这种情况下，故障一般恰好发生在换相过程之中或刚要换相时，且故障相参与此次换相过程。此时，需要对交流边界元件电流的变化量进一步分析。前文已经指出，星形/星形桥和星形/三角形桥上的换流器不会同时发生换相失败，可以分别进行分析。对于星形/星形桥和星形/三角形桥，分别以V1→V5和V2→V6换相过程为例分析，其余换相过程的结论可以类推。

1）星形/星形桥

正常运行时，V1→V5换相过程的触发时刻如附录A 图A7 所示。为了保证换相过程能够顺利进行，换相触发脉冲会在自然换相点前一个超前触发角β的时刻发出。超前触发角β满足：

式中：μ为换相重叠角，代表换相过程持续的时间，与正常运行时的电流大小相关，一般在20°左右；γ为关断角，是晶闸管电流降至0 到其开始承受正向压降的时间，正常运行时，逆变站控制系统一般将γ控制在15°～18°。

仿真结果表明，该工况下故障后1 ms 内逆变站提供的交流电流时域变化量不超过交流边界元件输出电流变化量的20 %。逆变站提供的交流电流时域变化量Δidc(t)与交流边界元件的电流变化量Δib(t)相比较小，即此时逆变站输出电流的影响较小。

2）星形/三角形桥

正常运行时，V2→V6换相过程的触发时刻如附录A 图A8 所示。仿真结果表明，该工况下故障后1 ms 内逆变站提供的交流电流时域变化量不超过交流边界元件输出电流变化量的20%。相应地，逆变站提供的交流电流时域变化量Δidc(t)与交流边界元件的电流变化量Δib(t)相比较小，即此时逆变站输出电流的影响较小。

综合上述分析可知，故障后的首个换相间隔的时间（1.67 ms）之内，无论是否发生换相失败，使用电流时域变化量进行线路电流和交流边界元件电流的相似程度比较基本不受逆变站输出电流的影响。

2 交流边界元件电流的推算方法

通过对逆变站近区线路出口故障特性分析可以得出，线路电流变化量与交流边界元件电流变化量之间的相似程度是区分出口故障方向的重要特征，因此，需要根据线路上可以测得的线路电压、电流获得交流边界元件的电流。可以采用电磁暂态计算的相关理论和方法，对交流边界元件的电流进行推算。

将逆变站换流母线上连接的所有有源支路（包含直流侧换流站和交流侧电源）的作用统一等效为一个电压源。等效之后，用于计算交流边界元件电流的电路可以简化为图2 所示的电路，其中，ueq(t)为等效电压源，其值等于线路保护装置的测量电压；R1、R2、R3为元件电阻；L1、L2为元件电感；C1、C2、C3、C4为元件电容。

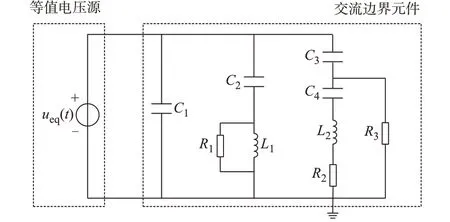
图2 求解交流边界元件电流的简化等值电路Fig.2 Simplified equivalent circuit for solving current of AC boundary element

利用隐式梯形积分法，可以将电路中的电感、电容元件等效为电阻与电流源并联的等效模型，如附录A 图A9 所示。电感、电容元件的等效电阻和电流源依式（7）和式（8）求解。

式中：C为电容；L为电感；Δt为电磁暂态计算的步长；uL(t)、uC(t)、iL(t)、iC(t)分别为t时刻的电感、电容元件的电压和电流；RC为电容等效电阻；IC为电容等效电流；RL为电感等效电阻；IL为电感等效电流。

将图2 所示电路中的电感和电容元件用附录A图A9 所示等效电路代替，得到交流边界元件电流的电磁暂态计算电路如图3 所示。图中：N1至N5为系统节点；N0为地节点；iacb为待求的交流边界元件电流；RL1、RL2分别为电感L1、L2的等效电阻；IL1、IL2分别为电感L1、L2的等效电流；RC1、RC2、RC3、RC4分别为电容C1、C2、C3、C4的等效电阻；IC1、IC2、IC3、IC4分别为电容C1、C2、C3、C4的等效电流。此时，可以通过节点电压分析法，求得任一时刻的节点电压，进而计算出交流边界元件电流。

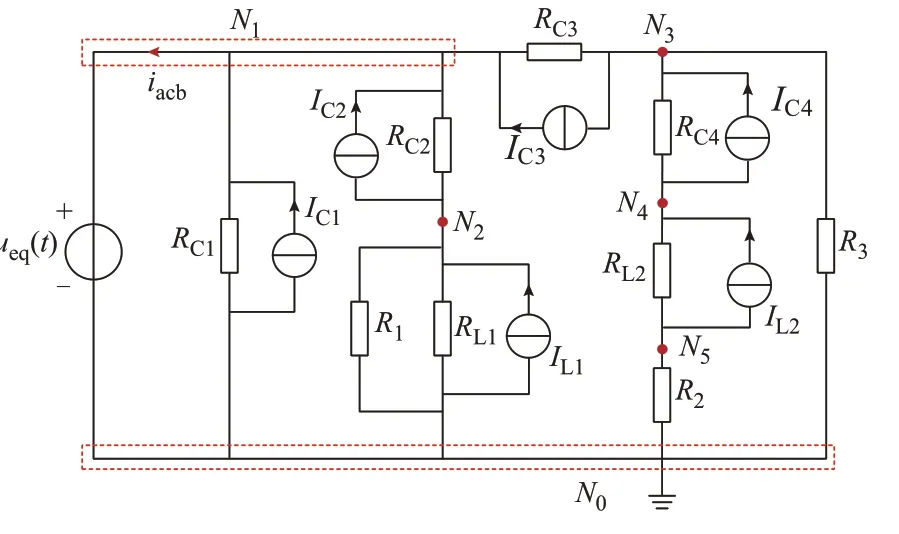
图3 求解交流边界元件电流的电磁暂态电路Fig.3 Electromagnetic transient circuit for solving current of AC boundary element

交流边界电流的计算流程如图4 所示，图中tmax为时间整定值，首先根据图3 所示的电磁暂态电路，列写节点导纳矩阵。进一步确定迭代的初始时刻，综合考虑迭代的精度和速度，可以将迭代初始时刻t0设置为故障前2 个周期的换流母线电压过零点。此时，交流边界元件中的动态元件储存能量低，由于迭代中使用的换流母线电压是准确的测量值，将其中的等值电流源设置为零带来的迭代精度误差将在很短的时间内消除，计算得到的交流边界元件电流能满足保护的精度要求，并降低了计算量。然后，根据线路测量电压和等效电流源的电流计算图3 所示各节点电压，进而可以获得各支路电流，即可获得当前时刻交流边界元件的电流。

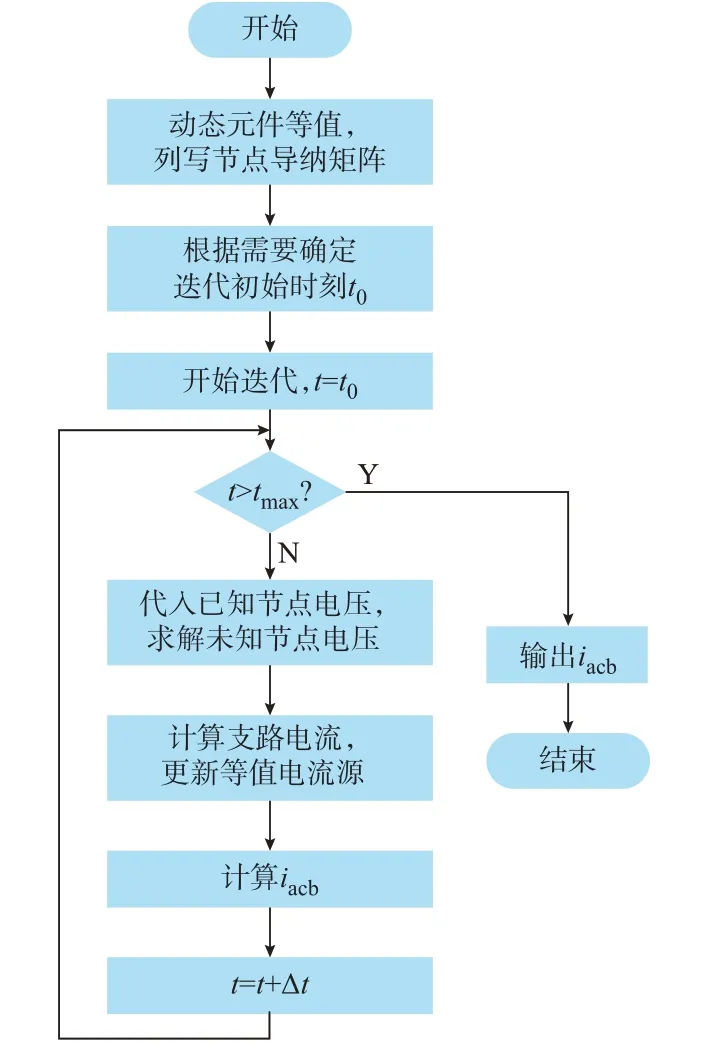
图4 交流边界元件电流的计算流程图Fig.4 Flow chart of calculation for AC boundary element current

3 基于波形距离系数的故障方向判别原理

3.1 波形距离系数

波形距离系数是表征两个波形之间空间距离的一种量度方法，其计算方法如式（9）所示。

式中：x(i)、y(i)分别为两个时域波形x、y在第i时刻的采样值；r(x，y)为两个波形x、y之间的波形距离系数；N为计算波形距离系数的数据窗长度。

根据波形距离系数的计算方法不难得出，任意两个波形的距离系数都在［0， 1］之间。若距离系数为1，则表示两个波形存在巨大差异；若距离系数为0，则表示两个波形完全相同。对于（0， 1）之间的空间距离值，越靠近0，则两个波形的相似程度越高；越靠近1，则相似程度越低。

3.2 保护判据

故障后的短时间内逆变站提供电流的变化有限，增长趋势较为稳定。因此，保护原理也仅在故障后的短时间内适用。对于12 脉动换流器，在正常运行时，两次换相过程之间的间隔为30°，即1.67 ms。考虑到保护原理本身是基于时域的分析，为尽可能减小逆变侧提供电流的变化对保护原理的影响，故所提保护原理仅在故障后的1 ms 内投入。

充分考虑用户需求。智慧乡村是为了向农村地区注入新鲜的生活血液，改变农村地区原有的单调的生活轨迹，打造一个充满活力、富有朝气、面向未来的地方。在各地方出台的智慧城市或信息化规划中，绝大部分包含“打造城乡一体的信息基础设施”这一任务，大部分农村地区已经开展了大规模的网络建设工作，但由于一些农村地区应用太滞后，造成了大量网络建设及维护资源的浪费，令人担忧。所以，就农村信息基础设施而言，建了不等于用了，用了不等于用好。因此，农村地区的网络布局应充分考虑农村地区市场需求，以人们需求为出发点和落脚点，不应强求达到城市地区的水平。

正向故障时，线路测量电流的变化量Δim(t)与交流边界元件电流的变化量Δib(t)相差较小，反向故障时两者存在显著差异。r(Δim(t)，Δib(t))为Δim(t)与Δib(t)之间的波形距离系数，具体的保护判据为：

式中：rset为保护整定值；r(Δim(t)，Δib(t))按照式（9）进行计算。

故障后连续10 个采样点满足判据式（10），则认为发生了正向故障；否则判断发生了反向故障。

所提方向元件与距离保护配合使用，解决出口近区金属性故障方向判别问题，其流程如附录A 图A10 所示。保护启动后，首先判断是否满足低电压判据，若满足则进入故障方向判别流程，若不满足则直接返回。其中低电压判据采用半周绝对值积分算法，具体如式（11）所示。

式中：um(t)为t时刻的保护安装处电压；Uset为门槛值，Uset设置为10%的额定电压半周绝对值积分值。

通过设置低电压门槛判据，可以避免因雷击以及内部扰动等干扰对方向元件的影响。

3.3 保护判据的影响因素分析和整定

由于所提算法是利用故障后暂态信息实现故障方向判别，因此需要快速的启动元件，可借鉴近年来暂态量快速保护的启动元件进行设计［27］。

由式（10）可知，所提算法是通过比较实测电流的时域变化量Δim(t)与推算的交流边界元件电流的时域变化量Δib(t)之间的相似度进行故障方向判别。由于实测电流中仍包含逆变站注入交流系统中的电流，逆变站注入交流系统电流的变化量会对保护判据产生影响。此外，电流互感器（CT）的测量误差也将对保护判据产生一定的影响。保护判据门槛值的整定需要充分考虑上述因素的影响。

根据参考文献［21］，可近似求解电网换相型高压直流（LCC-HVDC）的交流短路电流，交流系统故障后1 ms 内，交流短路电流i(t)可表示为：

式中：idi(t)为t时刻的直流电流；Br为换流器总桥数；n为变流器变比。

将仿真模型参数代入式（12），计算可得，发生换相失败时直流系统提供的短路电流变化量不超过交流系统边界电流变化量的20%。考虑故障后1 ms 内CT 并不会饱和，通常CT 暂态传变误差不超过10%。因此，考虑换相失败和CT 暂态传变误差的影响，发生正向故障时，计算的边界电流和实际测量电流之间的误差约为30%。

将误差代入本文所提波形距离系数算法中，当实际测量电流与推算电流误差为30%时，对应的波形相似度为：

考虑保留一定的裕度，本文波形距离系数的门槛值rset设置为0.25。

4 仿真分析

在PSCAD/EMTDC 平台中搭建图1 所示的系统，其中交流出线全长50 km，其参数如表1 所示，直流线路全长为1 000 km，其参数如附录A 图A11 所示，采样率设置为50 kHz，交流边界元件电流的迭代计算步长Δt取20 μs。为了抑制噪声对保护判据的影响，将电压和电流测量数据经过截止频率为500 Hz 的二阶巴特沃斯低通滤波器处理。

表1 交流线路参数Table 1 Parameters of AC line

4.1 逆变站近区交流线路故障特性仿真分析

4.1.1 逆变站电流的影响分析

在交流线路正向出口（F1）处分别设置如下类型的故障：故障场景1 为0.692 s 发生C 相接地故障；故障场景2 为0.696 s 发生A 相接地故障。对于故障场景1，逆变站在故障后首个换相过程中未发生换相失败，对于故障场景2，逆变站在故障后首个换相过程中发生了换相失败。

1）故障场景1

附录A 图A12（a）为故障场景1 下逆变站电流变化量与交流边界元件电流变化量的对比。可以看出，由于此时未发生换相失败，此时逆变站电流变化量很小，交流边界元件电流变化量很大。

附录A 图A12（b）为故障场景1 下线路电流变化量与交流边界元件电流变化量的对比。可以看出，此时线路电流的变化量与交流边界元件电流的变化量呈现出高度的相似特征。

2）故障场景2

附录A 图A13（a）为故障场景2 下逆变站电流变化量与交流边界元件电流变化量的对比。可以看出，由于此时发生了换相失败，相较于故障场景1，逆变站电流变化量变大，但交流边界元件电流变化量仍然远大于逆变站电流变化量。

附录A 图A13（b）为故障场景2 下线路电流变化量与交流边界元件电流变化量的对比。可以看出，即使逆变器电流变化量较故障场景1 时变大，交流边界元件电流变化量仍占线路电流变化量的主要成分，此时线路电流的变化量与交流边界元件电流的变化量仍呈现出高度的相似特征。

综合上述分析，在正向故障下，无论故障后的首个换相过程是否发生换相失败，线路电流的变化量与交流边界元件电流的变化量之间都具有高度的相似性。

4.1.2 不同方向故障特性对比分析

在0.69 s 设置不同类型的正、反向出口故障，线路测量电流变化量与推算的交流边界元件电流变化量Δi对比如图5 所示。对于AG、ABC 故障，电流变化量使用的是A 相电流的变化量；对于BC、BCG 故障，电流变化量使用的是B、C 相电流之差的变化量。其中，BC、BCG、ABC 故障引发了首个换相过程的换相失败，AG 故障没有引发换相失败。

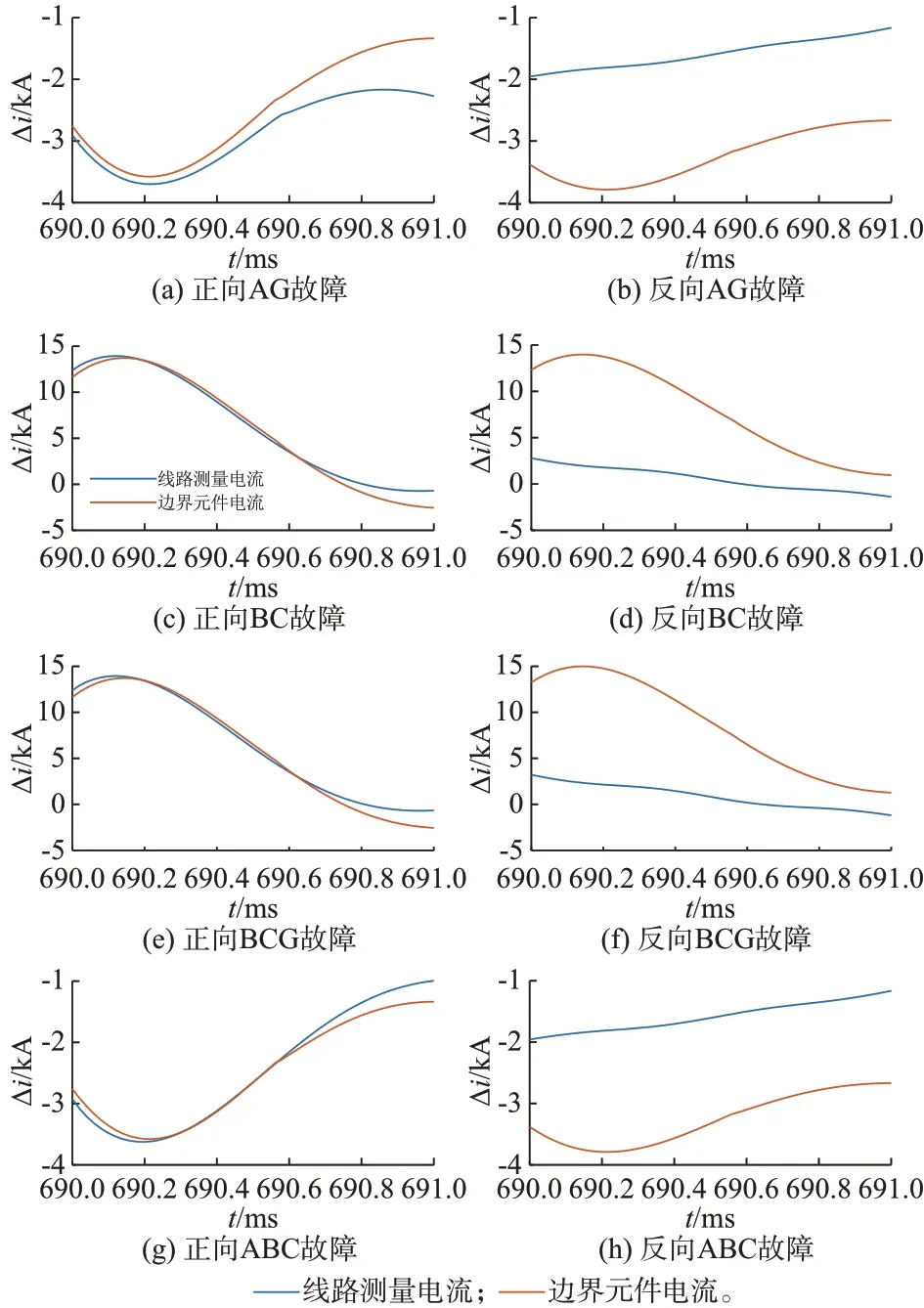
图5 不同故障类型下的电流变化量对比Fig.5 Comparison of current variations under different fault types

可以看出，在不同的故障类型下，无论首个换相过程是否发生了换相失败，正、反向故障下的两个电流变化量的相似程度都具有显著的差异。

4.2 保护判据仿真验证

4.2.1 不同故障类型的仿真

在0.69 s 设置不同类型的正、反向出口故障，交流线路测量电流变化量和交流边界元件电流变化量的波形距离系数如图6 所示。

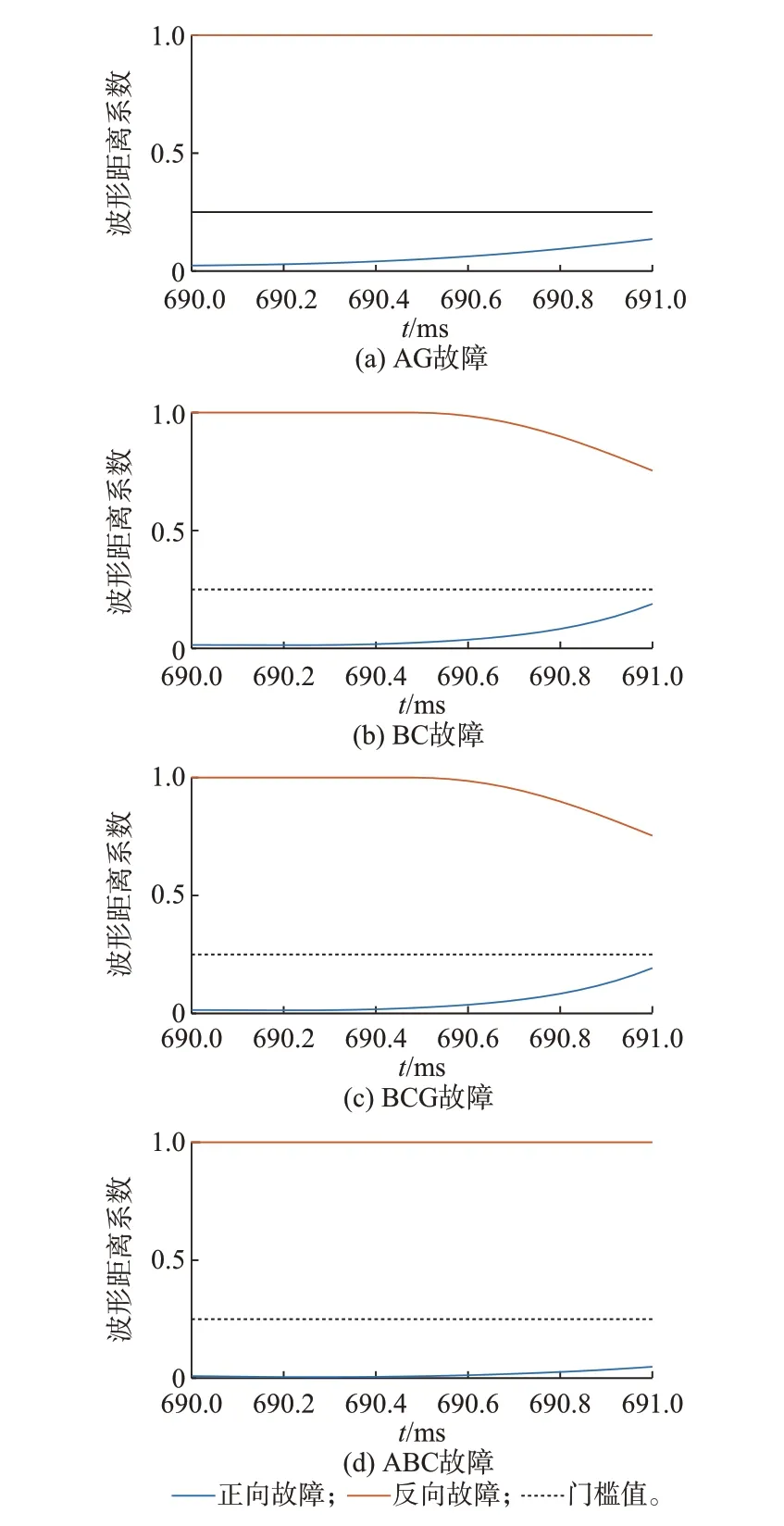
图6 不同故障类型下的波形距离系数Fig.6 Waveform distance coefficients under different fault types

从正、反向故障时的波形距离系数曲线可以看出，在同一时刻发生不同类型的故障时，反向故障时，波形距离系数一直维持在1 附近，呈现出较大的不相似程度；正向故障时，波形距离系数在故障后在0 附近。仿真结果表明，所提方向元件在不同故障类型工况下都能快速、准确地判别故障方向。

4.2.2 不同故障时刻的仿真

在0.692 s、0.694 s、0.696 s 和0.698 s 分别设置AG 故障，交流线路测量电流变化量和交流边界元件电流变化量的波形距离系数如附录A 图A14 所示。可以看出，在不同故障时刻，所提方向元件能快速判断出故障方向。同时也可以发现，在不同的故障时刻，反向故障时的波形距离系数在故障后的一段时间内出现下降，正向故障时的波形距离系数出现不同程度的上升。根据前述分析可知，这是由于不同故障时刻，逆变站电流变化量不同，使得正方向和反方向故障时计算的波形距离系数发生变化。不过并不会对方向元件的判别结果产生影响，从仿真结果可以看出，不同故障发生时刻，所提方法均能在故障后0.6 ms 左右准确判断故障方向。

此外，对其他故障类型在不同故障时刻下的故障进行了大量仿真分析，所提方向元件的判别结果如表2 所示。大量仿真结果表明，不同时刻发生各种类型的故障时，所提方向元件都能快速、准确地判别故障方向。

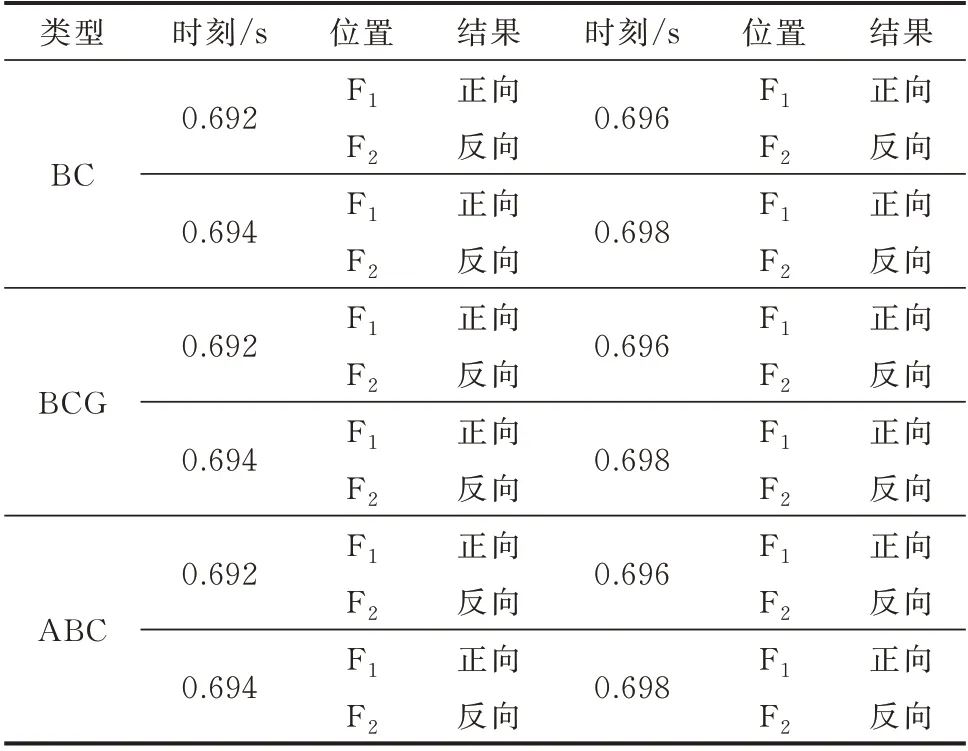
表2 不同故障类型和故障时刻下的保护动作情况Table 2 Protection operation with different fault types and fault moments

4.2.3 噪声的影响

为了验证噪声对所提保护的影响，在电压和电流测量数据中加入10 dB 的白噪声，仿真结果如表3所示。

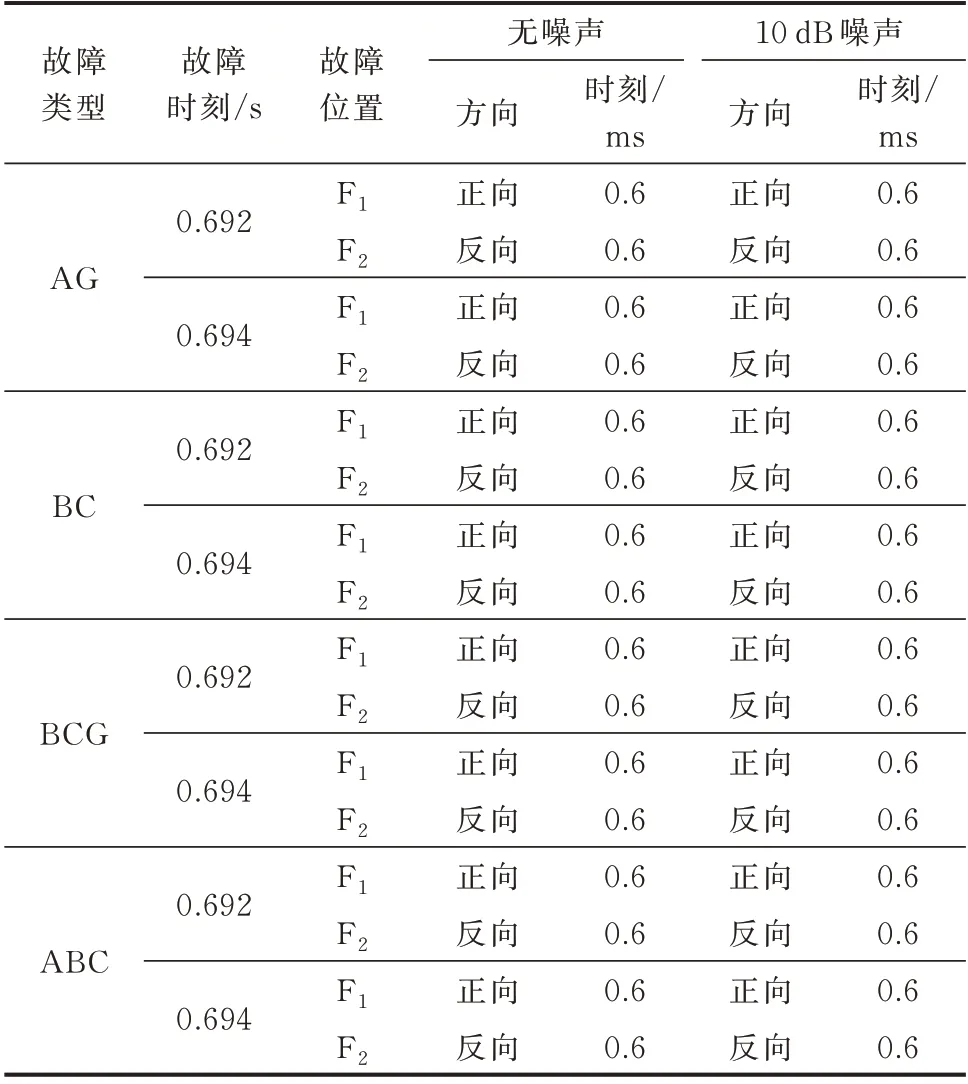
表3 噪声的影响Table 3 Influence of noise

表3 中仿真结果可以看出，当没有噪声时，在故障后0.6 ms 所提方向元件可以准确判断故障方向。加入10 dB 白噪声后，所提方向元件仍在故障后0.6 ms 能够准确判别故障方向。其原因在于，电压和电流测量数据均经过了低通滤波器处理，同时所提方向元件判据整定时留有较为充足的裕度。因此，噪声对所提方向元件的影响较小。

4.2.4 采样率的影响

上述仿真采样率均为50 kHz，为了验证较低采样率时所提方向元件的性能，分别设置采样率为20 kHz 和10 kHz，仿真结果如附录A 图A15 所示。

从附录A 图A15 可以看出，当采样率为20 kHz时，正向故障工况下，交流边界元件电流推算值与实际测量值存在较小的误差，不过不影响方向元件判别结果；当采样率为10 kHz 时，正向故障工况下，交流边界元件电流推算值与实际测量值存在一定的误差，但总体趋势保持一致，不影响方向元件判别结果。仿真结果表明，提出的方向元件在较低采样率时仍具有良好的性能。

4.2.5 迭代初始时刻的影响

前述仿真的迭代初始时刻选择为故障前2 个周期的换流母线电压过零点，为验证迭代初始时刻对算法的影响，分别设置不同的迭代初始时刻，仿真结果如附录A 图A16 所示。故障时刻设置在0.69 s，故障前2 个周期的换流母线电压过零点时刻在0.650 s，分别取迭代初始时刻为0.646 s、0.648 s、0.650 s、0.652 s。从附录A 图A16 可以看出，选择不同的迭代初始时刻，迭代算法基本在3 ms 左右就已经收敛，计算值基本与测量值保持一致。因此，所提迭代算法对初始时刻选取不敏感，具有良好的收敛特性。

5 结语

本文主要针对逆变站近区交流线路出口故障方向判别问题进行了研究。首先，分析了逆变站近区线路出口故障时线路电流与交流边界元件电流变化量之间的相似特征；然后，给出了一种根据线路测量电压、电流推算交流边界元件电流的电磁暂态计算方法；最后，提出了基于波形距离系数的故障方向判别原理。大量仿真结果表明，所提出的方向元件能够准确判断出口近区金属性故障方向，具有良好的动作性能。本文所提方向元件的性能会受到过渡电阻的影响，转换性故障工况下的性能有待提升。高压直流换流站故障特性与传统同步发电机存在显著差异，直流落点临近区域交流保护性能会受到影响，需要开展直流多落点区域交流保护新原理的研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。