电流差动保护在海上风电低频送出线路中的适应性分析

2024-01-19蒋嘉桁张晨浩宋国兵高校平吕艺超吴通华

电力系统自动化 2024年1期

蒋嘉桁，张晨浩，宋国兵，高校平，吕艺超，吴通华

（1.西安交通大学电气工程学院，陕西省西安市 710049；2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106；3.河海大学能源与电气学院，江苏省南京市 210098）

0 引言

近年来，海上风电获得了广泛的关注与发展，到2020 年全球已经有35 GW 的海上风电装机容量，其中中国占据了28.3%［1］。海上风电有3 种常见并网送出方式：高压交流输电、高压直流输电和低频输电［2-3］。低频输电在中远距离下，输送能力高于高压交流输电，经济效益优于高压直流输电［4-5］，在海上风电领域潜力巨大。

低频输电系统（low-frequency transmission system，LFTS）一般采用模块化多电平矩阵换流器（modular multilevel matrix converter，M3C）作为变频器，而低频海上风电场由永磁直驱风机（permanent magnet synchronous generator，PMSG）构成。两者均是电力电子型电源，与传统同步机电源相比，故障响应特性迥异。电流差动保护是传统交流系统中广泛应用的保护原理。对于海上风电低频送出线路，双端电力电子型电源对故障的不确定性响应可能影响电流差动保护的性能，有必要分析其在海上风电低频输电系统中的适应性，以帮助改进保护或提出新保护原理。

现有关于海上风电低频输电系统故障的研究多关注工频侧并网点故障［6-7］，对低频输电线路故障很少关注。此外，低频线路两侧电源均是弱电源，而目前对于含电力电子型电源系统的故障特征分析和保护适应性研究，局限于含有强电源的系统［8-9］，大多数为点对点的新能源送出系统［10-11］。海上风电经柔性直流（下文简称柔直）送出系统同为双端电力电子型电源系统，其交流侧输电线路故障已有一定研究［12-14］，可以为海上风电低频送出线路的故障分析与保护适应性分析提供借鉴。

目前，关于电力电子型电源系统中电流差动保护适应性已有一定研究。文献［15］从风电场的弱馈特性出发，根据两侧电流幅值差推导两侧电流相角差，进而判断保护适应性；文献［16］指出海上风电柔直系统中柔直换流器的控制和闭锁会影响保护性能，并提出了柔直换流器的短路电流解析表达式，但未具体分析保护适应性；文献［17］在两者基础上，分析电流差动保护在新能源场站经柔直送出系统中的适应性。但是上述研究均未详细考虑网侧电源的控制特性。文献［15］考虑并网系统为弱系统时，并未明确系统类型和控制策略；文献［17］并未考虑柔直换流器的负序控制。上述研究未能分析单相接地故障的情况，并且由于简化了故障网络对响应特性的约束，回避了故障电气量的理论计算。因此，仅能给出保护判据取值的大概范围，无法得出具体故障条件下保护的适应性结论，难以满足工程实际需求。

本文首先研究了系统故障网络数学模型、直驱风机和M3C 电源特性；接着，基于复合序网推导了故障电流与两端电源特性的关系，定性分析了两端电源特性对电流差动保护的影响；为解决定性分析无法判别的情况，提出基于改进节点方程的故障计算方法，并建立PSCAD/EMTDC 仿真模型验证了算法的正确性；在此基础上，建立了海上风电低频送出线路故障条件到保护判据取值的定量关系，从得到的保护判据取值范围和保护动作特性的匹配程度出发，定量评估了保护的适应性。

1 海上风电低频输电系统及其电源特性

1.1 系统拓扑结构

海上风电低频输电系统如图1（a）所示。该系统由海上风电场，低频输电线和岸上M3C 组成。风电场包括直驱式风力发电机组和集电系统。低频输电线由海底电缆和并联电抗器组成；并联电抗器采用欠补偿方式、双端补偿方案和星形接线；电流互感器安装在电缆和两端并联电抗器外侧；M3C 两侧有隔离变压器。

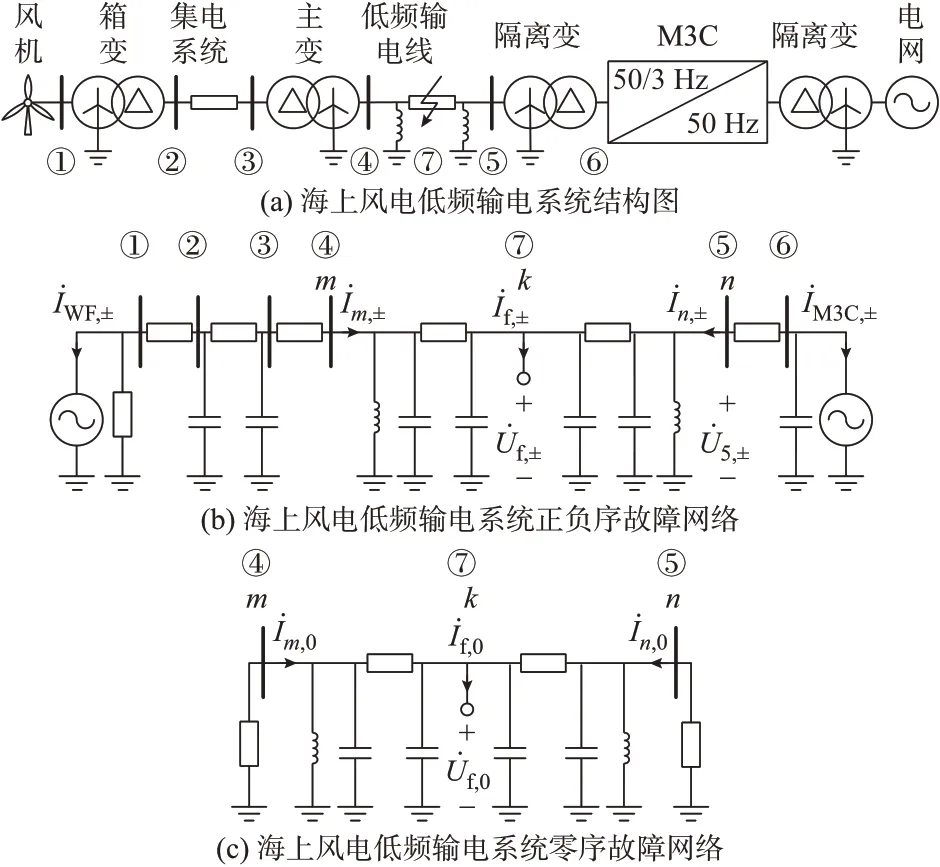
图1 海上风电低频输电系统拓扑Fig.1 Topology of low-frequency transmission for offshore wind power

在对系统建模时，除图1（a）中各元件等值模型外还考虑了风机端口的滤波器和M3C 端口的电容。考虑到地理位置分布对直驱风电场故障特性影响很小［18］，直驱风电场采用单机等值模型。

1.2 电源响应特性

海上风电低频输电系统中，直驱风机和M3C 有很强的控制能力，其故障响应特性完全由故障穿越策略决定。

1.2.1 直驱风机响应特性

海上风电场的风机控制策略可以参照现有风电场并网标准［19-20］，在故障时切换为低电压穿越控制策略，同时向电网提供动态无功支撑。再参考文献［21］的故障穿越阶段数学模型，可以得到故障稳态时直驱风机正负序电流的表达式为：

式中：θWF，+、θWF，-分别为正序、负序电压相角；İWF，+的d、q轴分量IWF，+，d、IWF，+，q的表达式如式（2）所示。

式中：PWF为风机额定输出有功；UWF，+为风机端口正序电压幅值；IWF，max为风机换流器电流限值；KWF，+为正序动态无功电流比例系数。

对于负序电流，目前直驱风机普遍采用的是负序电流抑制策略，将负序电流抑制为0。但是，最新的陆上风电标准［20］提出风机吸收一定的负序无功电流以抑制负序电压升高的策略。海上风电也可能采用，因此一并讨论，的d、q轴分量IWF，-，d、IWF，-，q的表达式为：

式中：KWF，-为负序动态无功电流比例系数；UWF，-为风机端口正序电压幅值。

1.2.2 M3C 响应特性

本文采取文献［22］中不对称故障控制策略。该策略采取双dq坐标变换［23-24］以实现低频侧和工频侧的解耦控制，因此低频送出线故障时可忽略工频侧控制的影响。M3C 故障稳态电压电流由外环控制决定，该策略的外环控制框图如附录A 图A1。该策略采取V/f控制为风电场提供电压支撑，通过改变其端口（节点6）电流控制隔离变压器端口（节点5）电压。在不对称故障时，该策略采用负序电流抑制，M3C 端口负序电流=0，而这可能导致M3C 非故障相过电压，故此时采取动态降压控制，根据负序电压幅值降低正序电压幅值参考值。在这种情况下，M3C 的故障响应特性表现为电压源特性，受控的节点5 正序电压表达式为：

式中：KM3C为正序电压降幅控制的比例系数；θM3C，ref为电压相角参考值。

M3C 还采取限流策略［25］，对d、q轴电流均设置了幅值上限，如附录A 式（A1）所示。实际中只有d轴电流会到达限值，q轴电流仍然能跟随外环控制目标。在这种情况下，M3C 输出电流的幅值达到上限值，但节点5 的q轴电压仍为0，故障特性可表示为：

综上所述，直驱风机和M3C 的控制策略均对故障电流进行了限制，直接改变了电流差动保护所依赖的故障特征，可能导致电流差动保护的不适应。直驱风机和M3C 输入电流对电流差动保护的影响将在下文讨论。

2 电流差动保护适应性分析

2.1 保护基本原理

电流差动保护原理基于基尔霍夫电流定律。比率制动型电流差动保护和比相式电流差动保护分别从幅值和相位的视角应用这一定律。

常见的比率制动型电流差动保护的动作判据如下：

比相式电流差动保护的动作判据如下：

式中：θmn为线路两端测量电流相角差；φb为保护闭锁角，对于100 km 长线路一般φb=43°，即动作区间为（-137°，137°）。

将式（7）代入式（8）可知θmn与有如下关系：

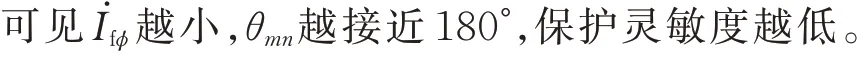
2.2 电源响应特性对保护影响机理

为简化推导，忽略图1（b）、（c）中的风机滤波器、M3C 端口电容、线路对地电容和并联电抗器等支路，结合故障边界条件［26］，可得到图2 所示不同故障类型下的复合序网络。图中：Rf为过渡电阻；Zm，+、Zn，+、Zm，-、Zn，-、Zm，0、Zn，0分别为正负零序网络中m侧和n侧阻抗之和。

参考图2，将故障边界条件与电流计算公式联立再相序变换，可以得到各相的和与电源输入电流的直接关系。为便于分析，单相故障以A 相为故障相，两相故障以B、C 相为故障相。

需要注意的是，由于线路两侧变压器的三角形接线，零序网络中不包含两侧电源，两侧电源并不直接控制零序电流。但是，两侧电源对负序电流的控制，将通过故障边界条件间接影响零序电流。参照图2（a），如果两侧电源将负序电流控制为0，相当于负序网络两侧开路，复合序网中故障电流无法形成回路，正序和零序电流也被控制为0。

但是，如果考虑风机滤波器、M3C 端口电容、线路对地电容和并联电抗器等支路，负序电流可通过以上支路形成回路，导致仍存在一部分故障电流，这是否能支撑保护动作，还需具体计算分析。

可见与AG 故障的情况十分类似，对负序电流的抑制将会抑制故障电流，导致保护灵敏性降低甚至可能拒动。

可见即便将负序电流抑制为0，故障电流还有两侧电源输出的正序电流。因此，保护理论上可以正确动作，但由于与的取值范围不确定，保护灵敏度仍需具体计算分析。

对于三相故障，以A 相为例：

故障电流由正序电流提供，保护理论上可以正确动作，但仍需计算与的取值范围以具体分析。

综上所述，虽然可以确定在AG 和BC 故障时，采取负序电流抑制策略会使得正负零序故障电流都减小，导致保护灵敏性降低甚至可能拒动。但由于取值范围不确定且没有直接的限定关系，并不能获得保护动作和灵敏度的绝对结论，还需具体计算分析。

而计算电源电流与计算系统各故障电气量是一体的。因此，需提出海上风电低频输电系统中故障电气量精确计算方法，进一步获得故障电流取值范围以分析保护适应性。

3 基于改进节点方程的故障电气量计算

故障时各节点电压的计算是测量点电流计算的前提，其总体思路是联立求解电源特性方程、节点方程和故障边界条件方程。电源特性方程由于控制切换，呈分段函数的形式；又由于dq轴解耦控制，需要将实部、虚部拆开；这些都导致直接求解方程组很困难，更可行的方法是数值求解方程组。为此，需将方程构造成以电压为自变量的差值函数的形式。

3.1 节点方程

根据正负零序网络可以得到对应的节点导纳矩阵和节点方程：

将式（16）与式（17）相减可得注入电流差值ΔI：

式中：ΔI+、ΔI-、ΔI0分别为正、负、零序注入电流差值，具体取值如附录A 式（A4）所示。

3.2 改进节点方程

根据M3C 电流是否达到限值，分别改写式（4）、式（5），得到如下方程替换方程组式（18）中节点6 正序分量相关方程：

AG 故障：

BCG 故障：

BC 故障：

三相故障：

为便于表达和计算，根据方程组式（18）中未改变项定义差值函数EⅠ，根据式（19）定义差值函数EM3C，根据改进节点7 方程定义差值函数Ef，具体表达式见附录A 式（A9）、式（A10）和式（A11）。则根据电源特性和故障边界条件改进后的方程组可表示为：

3.3 方程组求解及测量点电流计算

改进方程组中包含多个分段函数和绝对值运算，这使得求取方程组的雅可比矩阵十分困难。为避免计算雅可比矩阵，采用弦割法求解方程组［27］。

根据各节点电压可以计算系统任意节点电流，线路m、n测量点电流计算公式如附录A 式（A12）所示。

4 计算结果和仿真验证

4.1 算法正确性验证

以计算测量点m的电压电流为例。计算采用的系统参数：线路总长100 km，在m、n之间设置故障；风电场为50 台直驱风机等效，单台风机容量为2 MW；系统功率基准值为100 MW；其他系统参数见附录A 表A1。

为验证理论计算结果的正确性，根据算例的参数基于PSCAD/EMTDC 搭建仿真模型，将仿真值与理论计算值相比较。

附录A 表A2 和表A3 展示了不同故障类型和故障位置在两种控制策略下仿真值和理论值的相对误差。而附录A 表A4 和表A5 展示了不同过渡电阻时的计算结果，故障位置设置在线路中点。可以证明算法在所有情况下都有较高的精度。

要注意的是，在风机端口电压很低时（如三相或两相接地故障金属性故障）。锁相环电网同步会出现问题［28-29］，风机输出电流并未到达其控制目标，即风机不符合前述数学模型，求解改进方程组无意义，故BCG 和三相故障过渡电阻不是从0 起。

4.2 计算结果和适应性分析

将计算得到的测量点电流代入保护判据公式中，可实现已知故障条件计算保护判据，得到保护判据取值随故障条件变化的曲线，进而研究保护在不同条件下的适应性。

4.2.1 比率制动型电流差动保护

图3 展示了理论计算得到的采取负序电流抑制策略，发生不同故障类型时，不同过渡电阻下故障相KⅠ随故障距离变化的曲线；x为故障点到m距离占线路总长之比。其他故障类型和控制策略的情况则汇总在附录A 图A2 中。

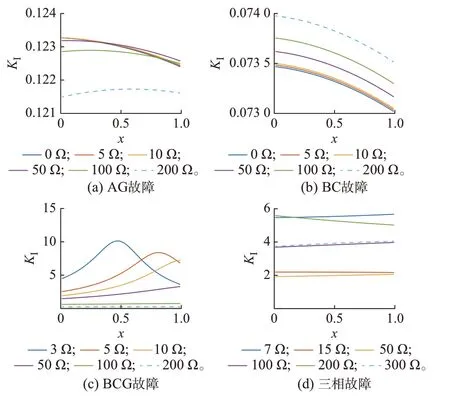
图3 负序电流抑制策略下KI的变化Fig.3 Changes in KI under negative sequence current suppression strategy

计算结果表明：AG 和BC 故障的KⅠ明显小于1，即可能小于Kres，保护有可能拒动；要保证保护动作只能取较小的Kres。特别是BC 故障且采取负序电流抑制的情况，KⅠ约为0.07，与无故障时KI很接近（无故障时KⅠ计算值和仿真值约为0.039 9），难以通过整定Kres使保护正确动作。对于BCG 故障：中、低过渡电阻时，KⅠ明显大于1，保护适应性良好，两种控制策略也无较大差异；高过渡电阻时，KⅠ明显减小，降至1 以下，保护灵敏度下降。对于三相故障，在高、中、低过渡电阻时，KⅠ都在1 以上，保护有良好的适应性。

4.2.2 比相式电流差动保护

图4 展示了采取负序电流抑制策略，不同故障条件下θmn的变化曲线，其他故障类型和控制策略的情况则汇总在附录A 图A2 中。

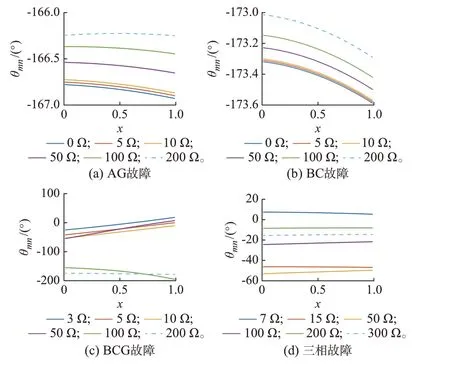
图4 负序电流抑制策略下θmn 的变化Fig.4 Changes in θmn under negative sequence current suppression strategy

计算结果表明：AG 和BC 故障时θmn在动作区间外，保护拒动，此时应适当减小保护闭锁角φb。对于BCG 故障，中、低过渡电阻时θmn在动作区间内，保护正确动作，但是在高过渡电阻时，θmn接近180°，保护灵敏度降低。对于三相故障，在高、中、低过渡电阻时，θmn都在动作区间内，保护有良好的适应性。

4.3 负序电流抑制策略对故障电流影响机理验证

为验证负序电流抑制策略对故障电流İfϕ的影响，对单相接地故障和两相短路故障的情况进行了仿真，如附录A 图A3 所示。如果忽略风机滤波器、线路对地电容和并联电抗器等支路（M3C 端口电容用于稳定电压，去掉后M3C 无法稳定），故障电流趋近于0，与理论分析相符；但若考虑完整系统模型，计及风机滤波器、线路对地电容和并联电抗器的影响，就仍会有一定故障电流存在。但即便如此故障电流也很小，保护仍有拒动风险。

为进一步验证单相接地故障时负序电流抑制策略对零序电流分量的影响，在3 个条件下进行了仿真：1）风电场采取负序电压抑制策略；2）风电场采取负序电流抑制策略；3）风电场采取负序电流抑制策略同时去掉风机滤波器、线路对地电容和并联电抗器。零序差动电流幅值|İm，0+İn，0|仿真结果如附录A 图A4 所示。可见负序电流抑制策略的确会抑制零序电流，导致保护灵敏度下降甚至拒动；但风机滤波器、线路对地电容和并联电抗器的存在也保证了仍会有一定零序电流存在。