基于叠加原理的综合能源系统动态潮流追踪及碳熵分析
2024-01-19王梦雪赵浩然刘春阳马后震
王梦雪,赵浩然,刘春阳,马后震
(电网智能化调度与控制教育部重点实验室(山东大学),山东省济南市 250061)
0 引言
中国“碳达峰·碳中和”工作开局良好[1],能源侧改革在减排工作中作用显著。而综合能源系统(integrated energy system,IES)“源随荷动”的特征标志着需求侧在节能减排中将发挥重要作用[2-4]。用户的用能行为在碳权交易市场中受配额与交易准则[5-6]的约束,而在碳信号的引导下,用户能通过低碳需求响应[7-9]反作用于能量系统,成为能源侧改革的有力补充。
用户碳排放责任的有效界定依赖于准确的碳轨迹追踪。在IES 碳轨迹追踪的研究中,电力系统的研究较多。文献[10-13]基于比例共享原则提出了碳排放流理论,使用直流潮流将源侧碳排放分摊至荷侧;文献[14-15]基于复比例共享原则计及了损耗、无功功率对有功功率分布的影响;文献[16]基于电流理论确定源与损耗、负荷的能量关系,进一步计算碳排放分摊。但目前气、热系统的相关研究较少,只有文献[17-18]将电力系统的碳轨迹追踪方法扩展应用于IES。该方法通过碳指标的逐节点递推计算系统碳指标,无法形成解析的源荷关系。
准确的碳轨迹追踪依赖于简洁合理的潮流追踪方法。气、热系统潮流动态特征均通过一组描述状态量时空分布的偏微分方程进行刻画,现多使用有限元法与时频域转换法对其简化处理。文献[19-21]分别使用Euler、Wendroff 与3 层显式差分格式进行差分,但节点状态量依赖空间微元状态量的递推,求解效率低。文献[22-28]将气、热时域模型转换至频域和复频域,类比电力系统分别提出了统一能路理论与广义电路分析理论。但前者简化中引入了截断误差,且时频域序列对应关系复杂,难以形成直观的源-荷潮流关系;后者使用了较多假设,且使用主导时间常数简化气网管道集中参数模型,误差较大。文献[29]建立了气网管道的传递函数模型,提出了保留多个时间常数的简化方法,但未扩展至系统维度。
上述潮流模型不能精确计算源-荷潮流关系,无法形成简洁的潮流追踪方法。笔者碳熵系列论文的首篇文章引入“碳熵”描述碳排放可加性与传输损耗导致能量流碳排放密度增加的特点,提出的稳态碳熵分析方法将碳熵的可加性与电、热系统的叠加原理相结合,将传输至不同负荷的功率流、碳排放流直接从源侧分解,于荷侧叠加后形成明确的源-荷碳熵关系与精细碳指标[30]。该稳态碳熵分析方法适用于负荷变化小、动态过程短的电热互联IES,针对负荷变动大、动态过程长、时间尺度相差大的IES[31-32],则需使用动态碳轨迹追踪方法进行精确求解。
在文献[30]的基础上,结合IES 动态碳熵的分析需求,本文开展了如下工作:1)将天然气负荷、热网源节点温度的变化量作为激励,构建天然气系统、热网的传递函数矩阵,建立基于气、热系统叠加特性的动态潮流追踪模型,明确源-荷潮流关系;2)将碳熵的可加性与气、热系统动态潮流的叠加特性相结合,提出气、热系统的动态碳熵分析方法,明确源-荷碳熵关系;3)以中国吉林省某地区IES 为例对系统进行动态潮流、碳熵分析,并与稳态碳轨迹追踪方法对比,验证了碳轨迹追踪计及系统动态特性的必要性。
1 基于叠加原理的气、热系统动态潮流追踪模型
1.1 天然气系统动态潮流追踪模型
1.1.1 天然气系统管道模型
天然气系统中气流受压力驱动沿管道传输,满足质量守恒方程式(1)与动量守恒方程式(2)。
式中:ρ、v、p分别为天然气密度、速度和压强;g为重力加速度;λ、θ、D分别为气网管道的摩擦系数、倾角和内径;t、x分别为时间、空间坐标。
对式(2)进行简化,转换至复频域中求解气网管道传输特性方程,见式(3),推导过程见附录A。
式中:G0(s)、Gn(s)分别为气网管道首、末端气流质量流量;p0(s)、pn(s)分别为管道首、末端气体压强;A3(s)、B3(s)、C3(s)、D3(s)为气网管道传递函数矩阵中的元素。由于G0(s)、pn(s)的拉氏逆变换极难求解,需要对式(3)进行简化。
Gn、p0可表示为多个阶跃函数的叠加,即
式中:q、ϑ分别为Gn阶跃变化量的序号、个数;q'、ϑ'分别为p0阶跃变化量的序号、个数;ξq、ξq'分别为第q个、第q'个阶跃变化量的幅值;tq、tq'分别为第q个、第q'个阶跃变化量的起始时间;ε(t)为阶跃函数。
以Gn、p0的单位阶跃变化量作为激励化简G0、pn的单位阶跃响应矩阵,保留单位阶跃响应中的阶跃环节与有限个惯性环节[29],具体过程见附录A。则G0(s)、pn(s)的单位阶跃响应矩阵见式(5),G0(s)、pn(s)可表示为式(6)中有限个阶跃响应的叠加。
式中:Hpipe(s)为简化后的G0(s)、pn(s)单位阶跃响应矩阵;h1(s)、h2(s)、h3(s)、h4(s)分别为简化后的A3(s)/s、B3(s)/s、C3(s)/s、D3(s)/s;ξqe-stq、ξq'e-stq'分别为第q个、第q'个阶跃变化幅值与相移的乘积,能够改变单位阶跃响应的幅值与相位。
该方法不仅降低了拉氏逆变换难度,提高了计算效率,还得到了矩阵Hpipe(s),其由管道特性决定,在计算中保持不变。当Gn(s)变化时,可直接计算气网管道首端的气流响应,通过叠加响应计算状态量。
1.1.2 天然气系统网络模型及潮流追踪模型
由气网管道建模方法可知管道二端口模型为:
式中:sHpipe(s)为简化后的管道传递函数矩阵。
调整输入、输出可得:
式中:A4(s)、B4(s)、C4(s)、D4(s)为调整后气网管道传递函数矩阵中的元素。
根据式(8)建立气网所有管道的二端口模型[33],即
则气网节点注入气流质量流量(以下简称为气网节点流量)可表示为:
式中:GN(s)为气网节点流量向量。
气网中已知量一般为气源节点的压强与中间节点、负荷节点的气流量,按状态量已知情况调整式(11)。同时,为使未知量的拉氏逆变换顺利进行,使用处理管道阶跃响应矩阵的方法简化系统阶跃响应矩阵,可得基于叠加特性的天然气系统潮流模型为:
至此,天然气系统动态潮流模型已完全建立。从式(12)与图1 可知,气源节点流量可表示为多阶跃响应的叠加,Hsyst(s)保持不变,当负荷变化时,可以使用变化量的幅值、相位与Hsyst(s)计算气源节点流量的响应,通过叠加响应整体计算气源气流量。
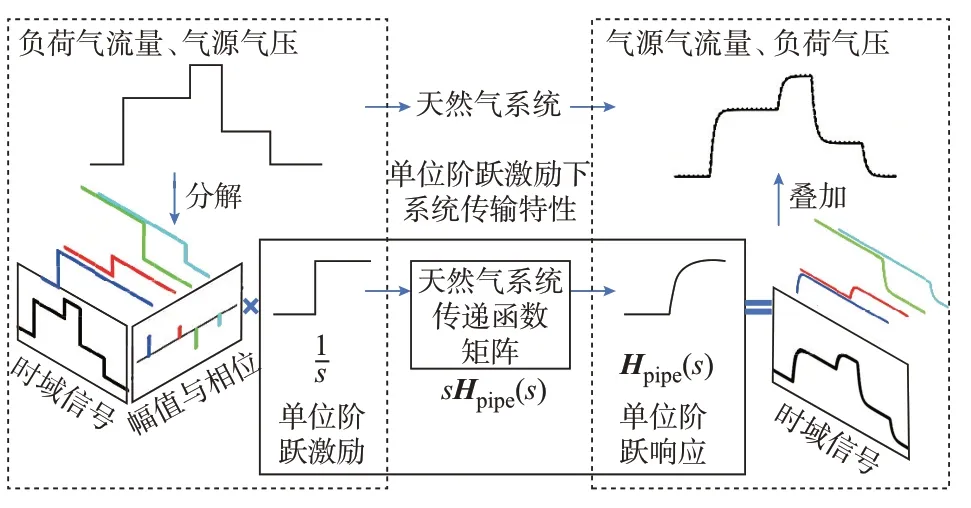
图1 天然气系统叠加特性Fig.1 Superposition characteristics of natural gas system
基于天然气系统的叠加特性构建潮流追踪模型,如式(13)所示。
式中:Gsc(s)为气源节点流量分量矩阵;Hsyst,11(s)、Hsyst,12(s)、Hsyst,21(s)、Hsyst,22(s)为Hsyst(s)的分块矩阵,Hsyst,11(s)、Hsyst,12(s)的矩阵维度分别为ngs×ngs、ngs×(ngn-ngs),其中,ngs为气源节点的数量,ngn为气网节点的数量。
使用拉氏逆变换将Gsc(s)转换为时域,即可求得任意时间断面气网的源荷作用关系。其中,气源节点对气压状态量已知的节点(气源节点)气流作用分量之和为0,因此可在碳轨迹追踪时只考虑气源节点对负荷节点的气流分量。
1.2 热力系统动态潮流追踪模型
1.2.1 热力系统管道模型
热网中的热量随传热媒介(本文为水)流动而传递,满足式(14)所示方程。
式中:T为水与环境的相对温度;m为水的质量流量;c、ρ'、γ0分别为水的比热容、密度、径向热扩散系数;μ为热网管道的导热系数;A'为热网管道截面积。
由于水的热导率极低,通常忽略第3 项水流内部的静态热传导,转换至复频域求解一阶线性齐次微分方程得:
式中:T0(s)、Tn(s)分别为热网管道首、末端温度,l'为热网管道长度;e-α、e-sβ分别为热网管道的热损、时延因子。
将T0表示为阶跃激励的叠加,即
式中:q″、ϑ″分别为T0阶跃变化量的序号、个数;ξq″为第q″个阶跃变化量的幅值;tq″为第q″个阶跃变化量的起始时间。
将式(16)代入式(15),可得Tn(s)为:
式中:H'pipe(s)为热网管道末端温度的单位阶跃响应;ξq″e-stq″为第q″个阶跃变化量幅值与相移的乘积。
由式(17)可知,Tn可以表示为阶跃响应的叠加,当T0变化时,可通过叠加响应计算Tn。
1.2.2 热力系统网络模型及潮流追踪模型
由热力系统叠加原理[34]可知,质调节的供热网与回热网的非源节点温度可由源节点温度表示。当热网源节点温度Tsr(s)表示为式(18)时,非源节点温度Tns(s)可写为式(19)。具体推导过程详见附录A。
式中:ζsr(s)为源节点温度变化量的幅值与相移乘积的向量;ζsr,r(s)为ζsr(s)中的第r个元素;H'syst(s)为热网的单位阶跃响应矩阵;ξq″,r和e-stq″,r分别为源节点r第q''个阶跃变化的幅值和相移。
热网叠加特性如图2 所示,Tns(s)可以表示为多阶跃响应的叠加,H'syst(s)保持不变,当Tsr(s)变化时,可使用变化量的幅值、相位与H'syst(s)计算Tns(s)的响应,通过叠加响应整体计算Tns(s)。
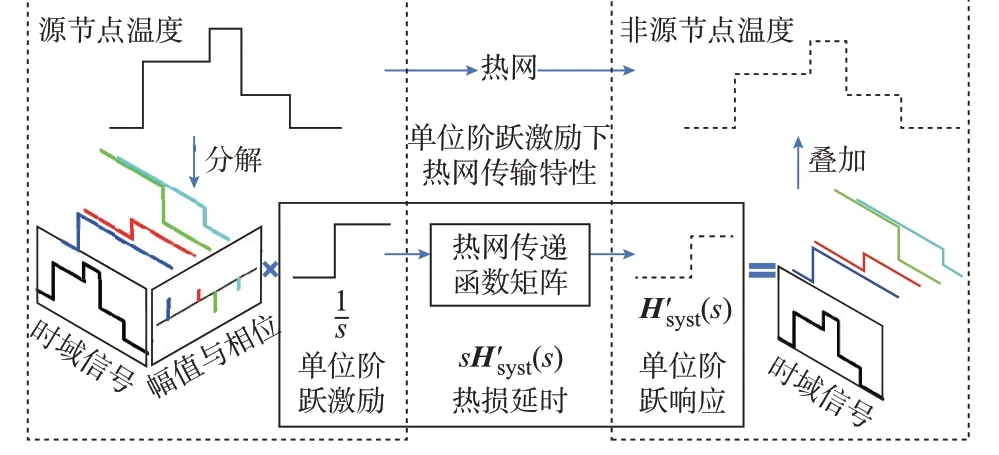
图2 热网叠加特性Fig.2 Superposition characteristics of heat network
供热网与回热网在热源处、负荷处温度满足:
至此,热力系统动态潮流模型已完全建立。基于文献[30]提出的使用无损传热模型求解源节点向非源节点传输总热量的方法,本文计及传输时延建立热网动态潮流追踪模型,求解各个热源的热量经不同传输时延后到达非源节点处的热量。需要注意的是,“无损传热模型”计算的是无热量损失时热网负荷处的热功率分配,其包括经有损传热实际传至热网节点的热功率和管道中损耗的热功率。
供热网与回热网动态无损传热下温度分布为:
式中:Tnoloss,ns(s)为无损传热下热网非源节点的温度分量矩阵,每一列元素为单个源节点作用下非源节点的温度;H'syst,noloss(s)为无损传热下热网的单位阶跃响应矩阵,为附录A 式(A13)仅考虑管道传热时延时求得的。
在质调节的热网中,节点处热量与温度成正比,则源节点与非源节点的温度作用关系可以表示源节点与非源节点的热量供应关系。
2 考虑动态特性的气、热系统碳熵分析
碳熵的可叠加性与源-荷潮流关系的可叠加性是碳熵计算与潮流模型的根本结合点,本文气、热系统分别基于气流动态响应、热媒质量流量的动态传输建立源-荷潮流关系,结合碳源节点的碳强度即可进行动态碳熵的分析与计算。
2.1 考虑动态特性的天然气系统碳熵分析
天然气系统动态特性对碳排放分摊的影响体现在:负荷变动率先引起管存变化,气源变化滞后,一定时间后达到稳态。因此,天然气系统的碳熵分析除了明确源-荷潮流关系外,还需计入管存的影响。
以阶跃型气流负荷为例绘制气源气流响应,如附录B 图B1 所示。图中:负荷曲线为蓝色实线。如前文所述,气源气流对阶跃型负荷的响应为阶跃环节与多个惯性环节的叠加,因此气源气流响应变化趋势如黑色实线所示,二者之差即为管存的变化量。气负荷增加时,负荷节点流量由管存消耗Gpk-和气源输入Gsc两部分供给;气负荷降低时,气源输入的气流同时支撑负荷与管存增加Gpk+。
本文根据每根管道的管存变化对总管存的容量与碳强度进行更新,假设管存中天然气的碳强度处处相等。根据式(13)求得的气网源荷作用关系进行气网碳熵指标、节点碳强度的计算,步骤如下:
步骤1:初始化t=0 时刻的气网管存总容量、管存碳强度、气源f的碳强度、气源f为气负荷j供应气流量占该气负荷的比例γf,j,t,其中,的计算公式为[35]:
式中:ΓG为天然气系统管道集合;Ta为气体温度;Ra为摩尔气体常量;Z为气体压缩系数;p0,b,t、pn,b,t分别为t时刻气网管道b的首、末端压强。


式中:Ω为气负荷集合为t时刻气负荷j质量流量降低时气源f产生的管存;为t时刻气负荷j产生的管存。
步骤4:重复步骤1~3 至全时段碳指标计算结束。
计算流程如附录B 图B2 所示。计算过程中可通过减小Δt来提高计算精度;为避免预设的γf,j,0、epk0与实际值相差较大,可在初始时刻前增加一段历史数据以提高求解精度。
天然气系统的动态潮流追踪为碳熵分析提供了解析的源-荷潮流关系,结合气源节点与管存的碳强度进一步明确源-荷碳熵关系后,通过叠加气源与管存传递至气负荷的碳熵分量,对气负荷的碳指标进行计算。
2.2 考虑动态特性的热力系统碳熵分析
热力系统碳熵分析的动态特性体现在热量传输的时延。不计时延的热量传输特性如附录B 图B3实线所示,当前时刻源A、B 的热量输入直接分配至负荷节点。但在传输时延的影响下,不同源节点的热量输入在不同时刻到达负荷节点,如图B3 中黑、红色虚线所示,源A、B 的热量须经时延ΔtA、ΔtB才能传递至负荷。由此导致计及时延时负荷温度与不计及时延时存在差别,如绿色虚线与蓝色实线所示,未考虑时延的潮流追踪难以形成准确的动态碳熵指标。
本文根据式(22)求得的计及时延的热力系统无损传热下源节点与非源节点的温度作用关系,结合文献[30]基于热力系统碳熵叠加特性推导的热网源节点与非源节点的碳强度关系,建立动态热力系统中供热网源节点-回热网非源节点间的碳强度关系:

热源处碳排放守恒,可进一步求得热网源节点的碳强度与热源碳强度关系,如式(30)所示。


热网的动态潮流追踪明确了供热网、回热网中源节点与非源节点的温度作用关系,基于此建立节点碳强度关系并进行节点碳强度的求解。此外,基于源节点与负荷节点的碳强度关系,可以进一步分析源节点与负荷节点的碳熵关系。
2.3 耦合设备碳熵模型
基于碳排放守恒建立耦合设备的碳熵模型[30]如下:式(33)为单输入单输出设备(热泵、燃气锅炉等)的碳熵模型,式(34)为以热电联产机组为例的单输入多输出设备的碳熵模型。
式中:ein为耦合设备输入能量的碳强度;η、eout分别为单输入单输出耦合设备的转化效率、输出能量的碳强度;eout,e、eout,h分别为热电联产机组备输出电能、热能的碳强度;ηe、ηh分别为热电联产机组的产电、产热效率系数。
3 算例分析
本文算例分析包括气、热网的管道模型仿真分析与IES 的仿真分析。气网管道参数见附录C表C1,将本文提出的气网管道动态建模方法与微元法进行建模对比,以验证本文所提模型的有效性;热力管道参数见附录C 表C2。本文以中国吉林省某地区IES[23,36-37]为例建立动态潮流及碳熵模型,具体拓扑见附录B 图B4,图中箭头方向为能流方向。
在动态潮流分析中,使用本文提出的动态模型计算气、热系统的动态潮流,电力系统运行时间尺度极短,因而使用稳态模型进行计算。气、热系统模型均使用拉氏变换进行时域与复频域转化,得到潮流唯一解依赖于系统的初始条件,本文使用历史边值代替初值的方法[38]对初始条件进行等效。电、热、气系统的数据交互时间间隔为1 min。
在动态碳熵分析中,本文着重对气、热系统进行碳熵分析,将文献[17]中气、热系统的稳态碳轨迹追踪方法作为对比方法,比较天然气系统和热力系统动态碳熵分析结果与稳态碳轨迹追踪结果的差别。其中,考虑到算例中天然气系统动态过程约20 min。因此,于负荷气流跃变后的0、10 min 处对管存容量与碳强度进行更新。为体现不同碳源碳强度对系统碳指标的影响,天然气系统包含2 类气源:天然气矿井与电转气设备。热力系统中包含3 类热源:燃气锅炉、热泵与热电联产设备。本文风电机组默认碳强度为0,煤炭碳强度为875 gCO2/(kW·h)[12],天然气矿井中天然气碳强度为200 gCO2/(kW·h)[17],电转气设备的天然气碳强度为50 gCO2/(kW·h)。
仿真环境为Intel Core i5-8500 CPU,16.0 GB RAM,使用MATLAB R2018a 进行建模。
3.1 管道模型分析
3.1.1 天然气系统管道模型分析
气网管道末端气流量以60 min 为跃变间隔,微元法中微元段长为900 m,微元数为20,本文所提方法在总管长不变的情况下改变微元长度、微元个数、惯性环节保留个数以测试本文所提方法的计算精度,测试结果如表1 和附录B 图B5 所示。
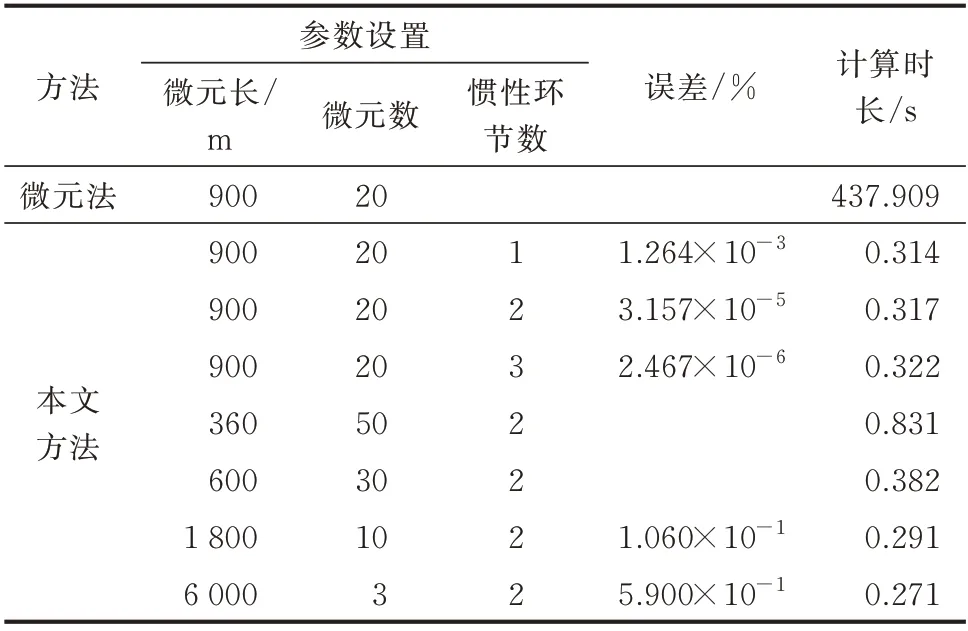
表1 气网管道模型数据对比Fig.1 Comparison of natural gas pipeline model data
由表1 可知,当本文所提方法保留2 个惯性环节时,增加微元长度,减少微元数,误差增大;当设置微元长度为900 m,微元数为20 时,保留1~3 个惯性环节所得气流量与微元法数据与附录B 图B5 中基本重合,误差均小于0.000 1%,说明本文所提方法的计算精度能够满足需求。此外,本文所提方法有运算优势,能够极大程度降低运算时间。需要注意的是,数据的数量级将随着微元数的增加而增加,MATLAB 中的舍入误差可能会导致求得的管道末端气压对首端气压的响应时长不稳定。由于管道首端气压保持不变,可通过在初始时刻前增加一段历史数据使末端气压对首端气压的响应到达稳态,以确保初始时刻后叠加气压对末端气流响应的动态过程的准确性与精度。本文方法在微元长度为1 800 m,微元数为10 时已具备较高的计算精度,且微元数的增加也将导致计算时间增长。因此,在计算过程中无须使用过高的分段数。
3.1.2 热力管道模型分析
附录B 图B6 中蓝色实线为热力管道首端温度,绿色虚线为热力管道末端温度。由图B6 可知,管道首端输入一定温度的工质,管道末端温度存在约17 min 的时间延迟和平均值为2.75 ℃的温度损耗。由于本文提出的热管道动态模型没有进行简化,计算结果即为精确数据。
3.2 IES 算例分析
3.2.1 电力系统潮流及碳熵分析
1)电力系统潮流
电力系统动态潮流数据如附录B 图B7 所示,节点电压幅值均介于1.02~1.03 p.u.之间,在12 h 内变化不大;电压相角介于0.002~0.014 rad 之间。
2)电力系统碳熵分析
电力系统节点碳强度如附录B 图B8 所示,电力系统负荷节点碳熵如附录B 图B9 所示,节点4 负荷为燃煤机组供电,其节点碳强度及负荷碳熵较高;节点2 处负荷由于为风电机组供电,其碳熵为0;负荷节点6、7 碳强度相差不大,但由于电负荷容量存在差别,其碳熵差距较为明显。
3.2.2 天然气系统动态潮流及碳熵分析
1)天然气系统动态潮流
天然气系统动态潮流数据如附录B 图B10 所示。负荷变动后,气源缓慢响应,约20 min 后进入稳态。需要注意的是,在10~11 h 的时间段内,节点1 处负荷不变,节点5 处负荷变化微弱,仅有节点3处负荷变化明显,根据图B4 气流方向可知,节点3处负荷仅由气源1 供气,但图B10 中,气源节点4、7对该负荷均进行响应。这是因为负荷气流量变化导致系统气压整体发生变化,进一步对气源的气流量产生影响,最终使得气源节点1、4、7 均对该负荷变化进行响应。
2)天然气系统动态碳熵分析
天然气系统节点碳强度数据如图3 所示,其中实线为动态碳熵分析方法的计算结果,虚线为稳态碳轨迹追踪方法的计算结果。气负荷节点3、5 碳强度在1 h 处存在较大变动,是因为该节点在t=0 时刻的气源气流供应比例γf,j,0与1 h 后气流供应比例相差较大;节点3、5 碳强度在后续动态过程中存在尖锋,是因为系统初始状态的管存碳强度较高,当负荷使用管存中的气流时,碳熵增大。节点1 动态碳强度保持不变是由于该处负荷气流量保持不变,两个气源一直以固定比例为负荷供气。
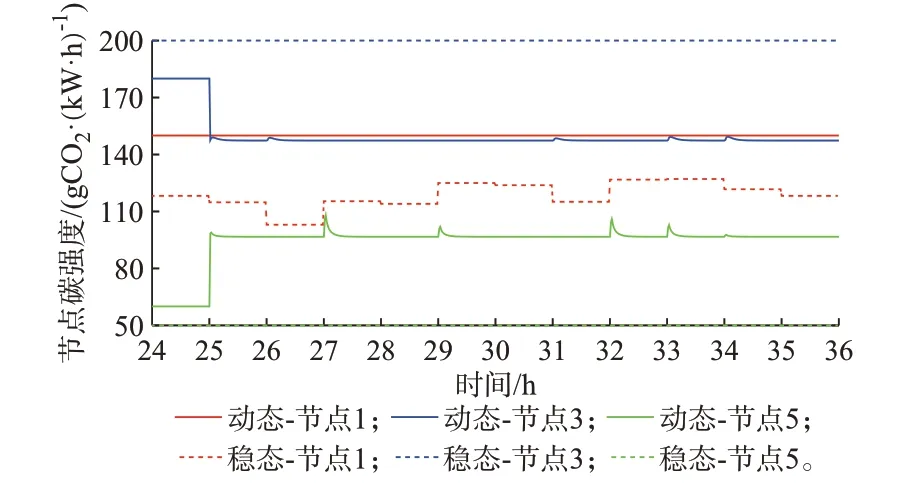
图3 天然气系统碳强度动态与稳态方法对比Fig.3 Comparison of carbon intensity in natural gas system between dynamic method and steady-state method
由图3 可知,使用稳态碳轨迹追踪方法求解动态天然气系统节点碳强度会产生较大误差,最大误差达53.947%。这是因为动态碳熵分析方法根据源对荷的气流响应将源传递碳熵分摊至负荷,而稳态碳轨迹追踪方法无法做到这一点。
天然气系统负荷节点的碳熵与功率分量见图4。使用本文提出的天然气系统动态碳熵分析方法可区分气负荷的碳熵来源。图中:紫色部分为气源4 传递至气负荷节点的碳熵;红色部分为气源7 传递至气负荷节点的碳熵;绿色部分为管存传递至气负荷节点的碳熵。由图4(c)可知,负荷节点3 处碳熵来源以气源4 为主,使用稳态方法计算求得的碳熵与动态方法相差较大,平均误差为35.638%,最大误差为44.584%,每小时碳排放最大相差4.617 tCO2。
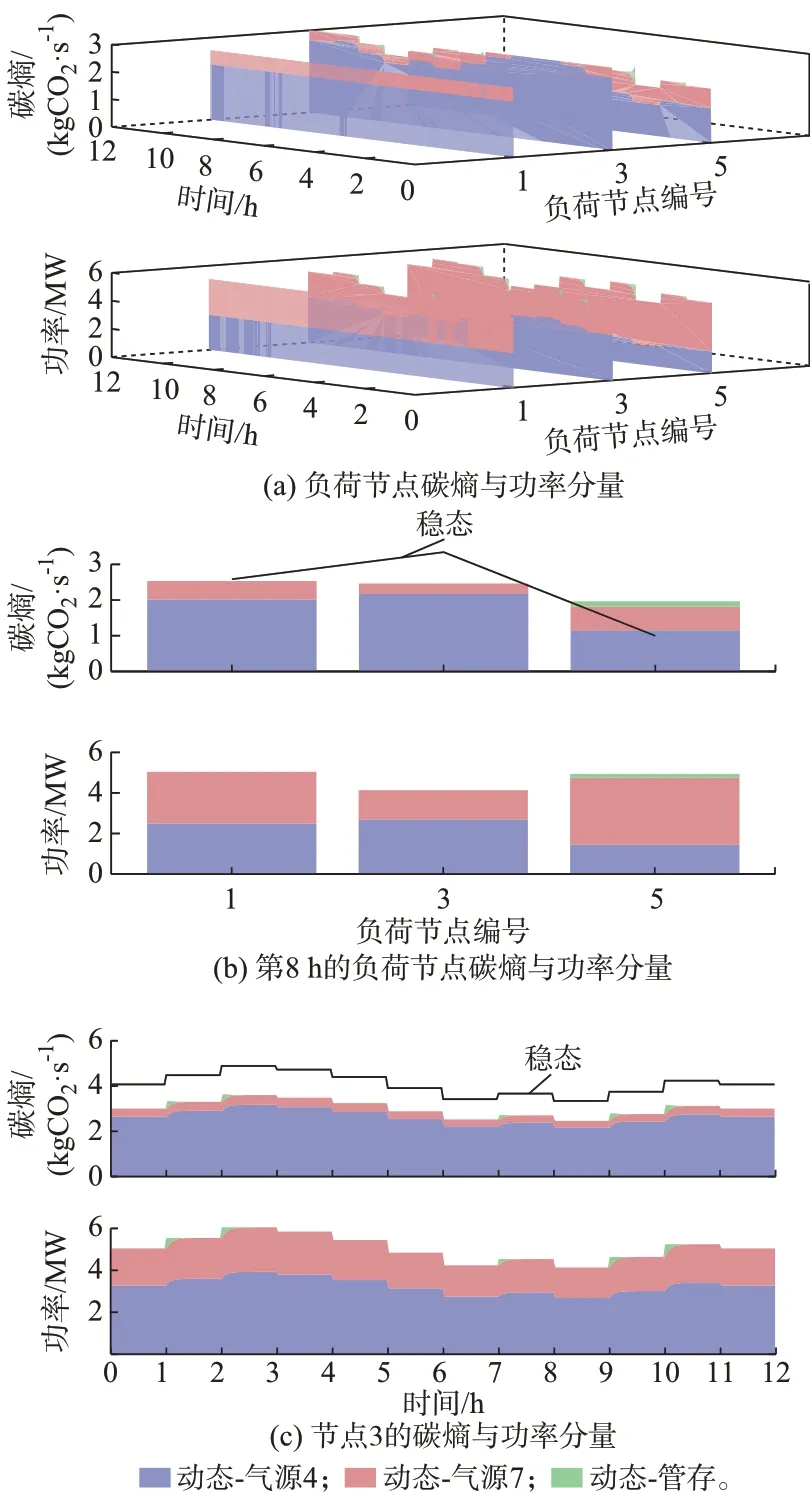
图4 天然气系统负荷节点碳熵与功率分量Fig.4 Carbon entropy and power components at load nodes in natural gas system
3.2.3 热力系统动态潮流及碳熵分析
1)热力系统动态潮流
热力系统3 个热源温度分别为90、88、89 ℃,使用本文建立的热力系统潮流模型计算得到的热源回水温度如附录B 图B11 所示。
2)热力系统碳熵分析
热力系统节点碳强度数据如图5 所示,从图中可以看出,使用稳态碳轨迹追踪方法在动态系统中计算碳强度也存在较大差距,该现象产生原因与天然气系统不同,这是由于稳态碳轨迹追踪方法在潮流追踪时将当下时刻的热量输入直接对应于该时刻的负荷输出,没有考虑该部分热量尚未传至负荷,而热力系统动态传热过程存在时延,不同热源的热量会经不同时刻到达负荷。稳态与动态潮流追踪结果的差异导致了碳强度的差异。
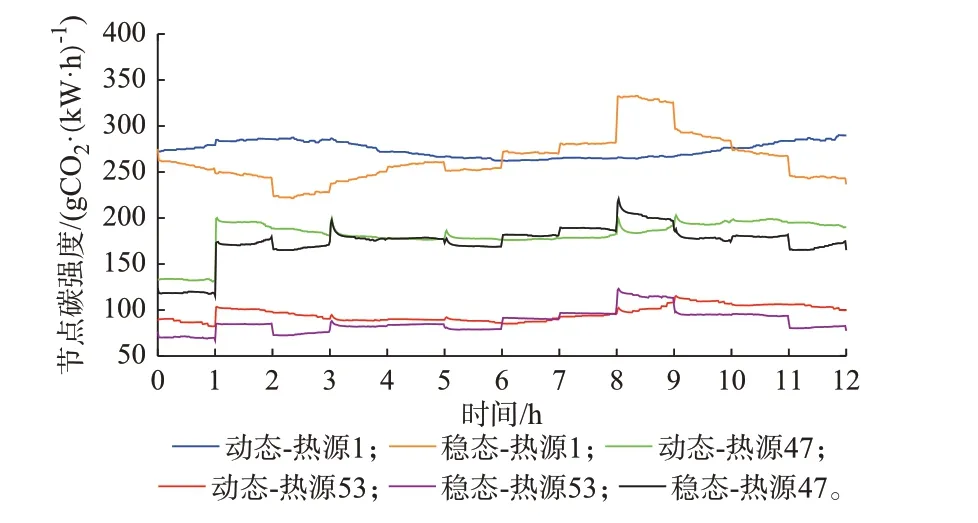
图5 热力系统碳强度动态与稳态方法对比Fig.5 Comparison of carbon intensity in thermal system between dynamic method and steady-state method
热力系统节点总负荷碳熵与功率分量见图6。使用本文提出的热力系统动态碳熵分析方法可以区分热负荷节点碳熵来源。图中:蓝紫色部分为热源节点1 传递至热负荷节点的碳熵;红色部分为热源节点47 传递至热负荷节点的碳熵;绿色部分为热源节点53 传递至热负荷节点的碳熵。由图6(c)可知,使用稳态碳轨迹追踪方法求得的碳熵与动态碳熵方法相差较大,平均误差为3.452%,最大误差为23.041%,每小时碳排放最大相差38.833 kgCO2,12 h 碳熵累计相差90.978 kgCO2。
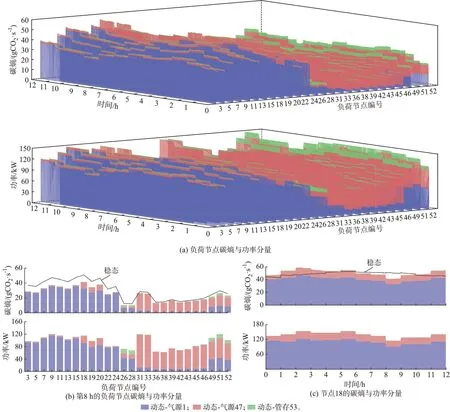
图6 热力系统负荷节点碳熵与功率分量Fig.6 Carbon entropy and power components at load nodes in thermal system
4 结语
本文首先基于叠加特性建立了气、热系统的动态潮流模型,并分别进行了动态潮流追踪,为碳轨迹追踪提供了明确的源荷能量关系。然后,提出了天然气系统与热力系统的动态碳熵分析方法,进一步明确了源荷的碳熵关系。最后,以中国吉林省某地区IES 为例进行计算分析,对比了稳态碳轨迹追踪与动态碳熵分析结果的差别。
1)本文建立的天然气系统动态潮流追踪模型计及了管存对负荷的气流响应,通过建立基于负荷变化量的系统传递函数矩阵,能够得到气源与管存对每个负荷变化的时域连续响应。
2)本文建立的热力系统动态潮流追踪模型通过无损传热计算了源节点对非源节点温度作用,考虑了热量传输过程的时延,能够对源节点传递至负荷节点的总热量进行准确计量。
3)本文提出的动态碳熵分析方法计及了IES 的动态特性,能够更加准确地界定用户的碳排放责任。此外,本文所提方法不仅能够计算负荷的总体碳指标,还能够分析负荷的碳熵成分,区分不同源对荷的碳排放作用。
在接下来的研究中,将考虑耦合设备的动态能量转换特性,建立更加精细、完善的能源站碳熵模型,并将本文所提方法应用于能源交易市场与碳权交易市场,为市场交易提供更加精确可靠的参考依据。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
