隧道消防输水管道泄漏信号增强技术研究

韩 霄,应迪清,汪成立

(1.浙江省交通运输科学研究院,浙江 杭州 310023;2.浙江大学 光电科学与工程学院,浙江 杭州 310027)

随着高速公路隧道的快速发展,隧道火灾安全保障问题正逐渐受到重视[1]。由于隧道相较于其他路段空间较为封闭和狭小,其出入口较少且相距较远,因此隧道一旦发生火灾,躲避和抢救会存在较大困难,如果不及时控制,极易造成较大的经济损失和人员伤亡[1-2]。保障隧道消防设施的完好性,既是火灾发生后能否得到及时有效扑救的先决条件,也是管理单位的管理职责要求[3-4]。消防输水管道是隧道中的重要消防设施之一[5],输水管道的泄漏会给隧道带来安全隐患。目前公路隧道中输水管道等消防设施的养护主要依据交通运输部发布的《公路隧道养护技术规范》(JTG H12—2015)执行,其中规定每1至3个月需要对给水管有无漏水进行1次检修[6],实际操作中,对输水管道的泄漏检测通常采用人工目测的方式,这使得输水管不仅状态信息存在一定滞后,而且检测数据也难以追溯,同时隧道中的来往车辆也会对检修人员的安全带来一定隐患。因此,需要研究非人工的、具有较好实时性的输水管道监测技术来解决上述问题。目前,针对输水管道的泄漏问题,国内外学者已经提出了多种监测技术[7-12]。林天翔等[13]于2021年研究了一种利用输水管道泄漏引起的振动信号振幅变化来对泄漏进行长期连续监测的技术,该技术通过安装在管道内的水声检波器来获得泄漏源的振动信号,在减少环境因素影响等方面具有一定的优势和可行性。然而,采用该技术的过程中,非泄漏状态下输水管道本身存在的振动信号背景噪声会给泄漏的检测带来一定的干扰[13]:一方面,对于较小的泄漏孔引起的微弱的振动信号幅度变化很可能被淹没在背景噪声中,从而造成对泄漏状态的漏检;另一方面,背景噪声幅度往往会受环境等各种因素的干扰而发生长期波动,这不仅有可能造成泄漏状态的漏检,还有可能引起非泄漏状态的误判。另外,该技术通常需要在恒定水压条件下实施,这就需要水泵长期频繁工作,一定程度上增加了水泵损坏的概率。因此,要实现这种输水管道泄漏监测技术的真正应用,需要通过深入研究对该技术进行进一步完善。

针对上述情况,笔者在林天翔等[13]的研究基础上,进一步提出一种泄漏信号增强技术。该技术利用了水泵启动加压开始和结束时两种状态下输水管道的水压差,通过监测两种状态下的振动信号幅度差的改变量来实现对泄漏的判定。由于该技术检测的项目是振动信号幅度差,因此在一定程度上减少了背景噪声幅度的长期波动对检测结果的影响。同时,该技术通过对水压差的优化增大了泄漏信号的强度,从而最终提升检测信号的信噪比。笔者首先通过理论推导说明了该技术的基本原理;然后通过数值仿真对该技术的特性进行了分析,根据该技术的特点提出了实现算法;最后通过数值仿真对算法进行了论证。

1 基本原理

笔者研究的隧道消防输水管道系统的基本框图如图1所示,该系统主要由输水管道、消防栓、水泵、控制系统和气压罐5部分组成[14]。

图1 隧道消防输水管道系统Fig.1 System of tunnel fire pipeline

隧道中的输水管道每隔一定的长度安装一个消防栓,从而将整个隧道的输水管道分成了多个等长度的区域。为了监测输水管道的振动信号,在每个消防栓附近的输水管处安装一个振动传感器,每段输水管对应了一个振动传感器,从而实现对输水管道振动信号的分段区域的分布式监测。

水泵用于当输水管道中的水压低于所设置的最小值时提供所需要的水压,气压罐用于使输水管道中的水压在一定范围内缓慢变化,从而减少水泵的频繁启动[14]。为了实时获得输水管道中的水压,在水泵出口段的输水管处安装了压强传感器。在实际水泵工作过程中,控制系统预先设定水压的最大值与最小值,压强传感器监测到的水压信号将反馈传输给控制系统,当水压低于预设最小值时,控制系统将控制水泵开始供水加压,直到压强传感器监测到的水压达到预设最大值时,控制系统将控制水泵停止供水加压[14]。整个隧道消防输水管道系统正是通过上述方法保证水压满足要求。

当输水管道发生泄漏时,泄漏声功率[13]计算式为

(1)

式中:v为水流泄漏速度;ρ为泄漏孔处水流密度;ρ0为水流初始密度;C0为隧道所在地声速;l为泄漏孔尺寸;K为比例系数;n为6～8的常数。假设水流密度及隧道所在地声速为定值,泄漏声功率[13]计算式为

PW=λvnS

(2)

式中:λ为常数;S为泄漏孔面积。根据伯努利方程[15-17],假设笔者研究的消防输水管道泄漏为小孔泄漏问题[18],泄漏声振幅A[13]计算式近似为

(3)

式中:μ为常数;p为输水管运行压强。将n设定为6.4,可以得到泄漏声振幅A计算式[13]为

A=Gp1.6S0.5

(4)

式中G=(λ/μ)0.5(2/ρ)1.6为常数。为了简化分析,将泄漏声振幅对参数G进行归一化,得到归一化泄漏声振幅A′计算式为

(5)

根据式(5),A′的单位为N1.6/m2.2。实际系统中,当压强传感器监测到输水管运行压强p小于最小设定压强p0时,水泵启动并对输水管道开始加压。为便于分析,假设水泵刚启动时的初始压强为p0,且启动后压强随时间t线性增加,因此水泵启动后的输水管道运行压强计算式为

p(t)=p0+kt

(6)

式中:k为水泵加压条件下单位时间的输水管道压强增加系数。假设当p达到最大设定压强pset时,水泵停止工作。根据式(5,6),水泵从开始启动加压直到达到最大设定压强pset的过程中,归一化泄漏声振幅随时间的变化可以表示为

(7)

由式(7)可以发现:在水泵启动加压过程中(即t<(pset-p0)/k),当没有泄漏,即S=0时,泄漏声振幅理论上恒为0,泄漏声振幅将不随时间发生变化;然而,当存在泄漏,即S≠0时,泄漏声振幅将随时间变化而发生变化。笔者利用这一特性提出输水管道泄漏监测技术。

2 泄漏声振幅特性

为了分析水泵启动加压过程中泄漏声振幅信号的特性,在不同情况下对归一化泄漏声振幅信号特性进行仿真。根据式(7),通过仿真得到的不同泄漏孔面积下A′随时间的变化关系情况如图2所示。仿真中的泄漏孔面积S分别设为2,4,8,14,18 mm2。其他仿真参数:p0=0.3 MPa;pset=0.5 MPa;k=0.005 MPa/s。根据仿真结果可以得到:当水泵刚开始加压时,A′随S的增大而不断增大;在水泵加压的过程中,A′会随时间不断增大,呈现出一个近似斜波信号的特征,且该斜波信号的斜率随S的增大而不断增大;当水压达到最大设定压强pset后,A′将保持恒定不变,且恒定后的A′随S的增大而不断增大。

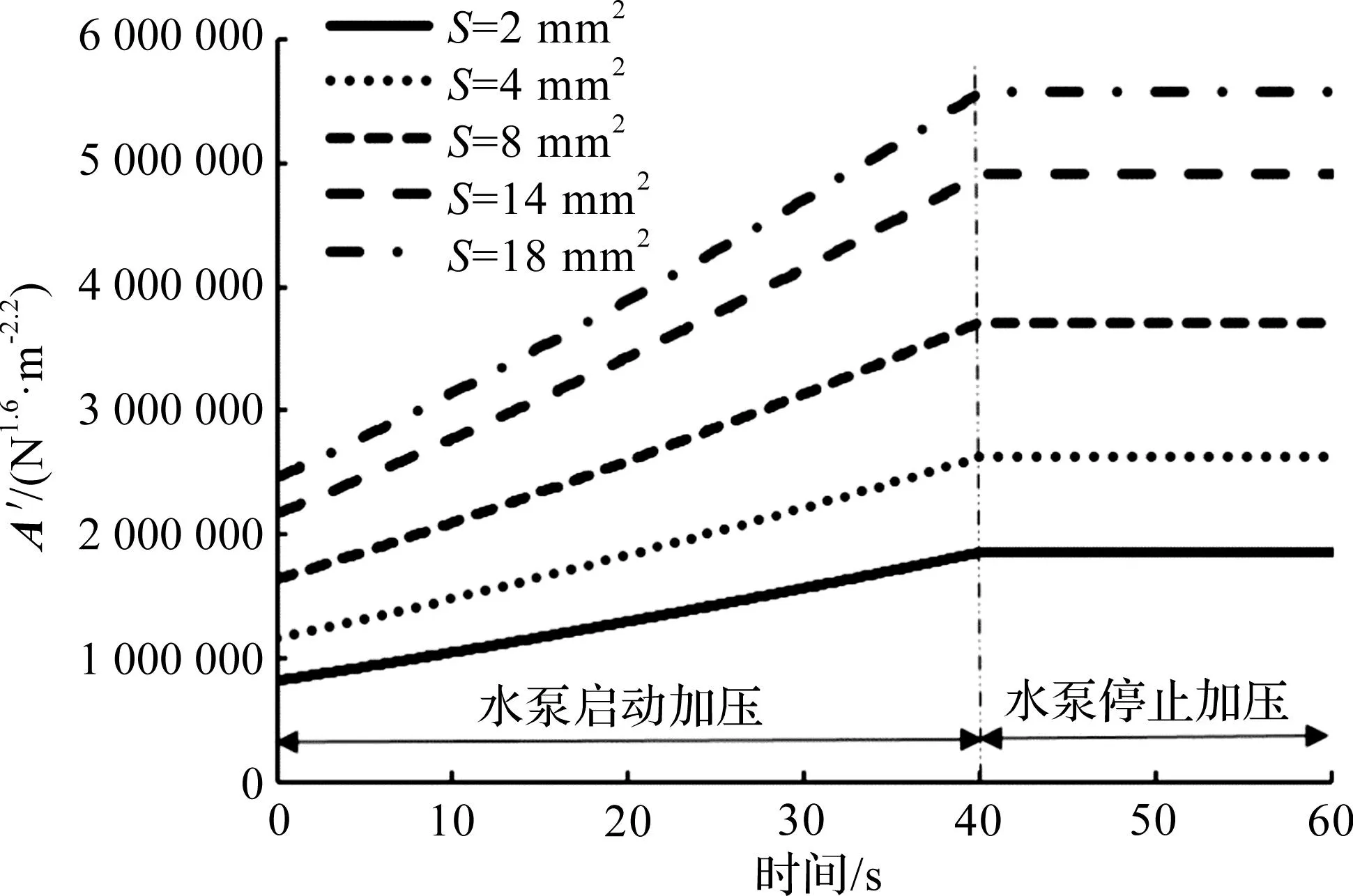
图2 水泵启动加压过程中A′随时间的变化Fig.2 Variation of A′ under process of pumping

设水泵刚启动加压时的归一化泄漏声振幅信号为A′0,且该振幅信号对应最小设定压强p0;设水泵刚停止加压时的归一化泄漏声振幅信号为A′set,且该振幅信号对应最大设定压强pset;设Δpset=pset-p0为设定的最大水压和最小水压的差。根据式(7),归一化泄漏声振幅信号在水泵加压前后的改变量ΔA′计算式为

(8)

根据式(8),仿真得到的不同Δpset条件下ΔA′随S的变化关系情况如图3所示。仿真中Δpset分别为0.2,0.3,0.4,0.5,0.6 MPa;p0为0.3 MPa。由图3可知:当S=0时,即未发生泄漏的情况下,ΔA′为0;当S≠0时,即发生泄漏的情况下,ΔA′会随S和Δpset的增大而不断增大。根据上述特性,笔者提出可以通过检测ΔA′对输水管道的泄漏情况进行监测。

图3 ΔA′随S的变化关系Fig.3 Relationship between ΔA′ and S

参考林天翔等[13]在恒定水压下通过监测振动信号幅度的变化来实现泄漏监测的研究方法,为了将该方法与笔者方法进行对比,对恒定水压下的振动信号特性进行分析。设pn=(p0+pset)/2为最小和最大设定压强的中间值,并假设在水压恒定为pn的条件下对振动信号幅度进行监测。根据式(5),通过仿真得到的不同Δpset条件下A′与S之间的关系情况如图4所示。仿真中Δpset分别为0.2,0.3,0.4,0.5,0.6 MPa;p0为0.3 MPa。当S=0时,即未发生泄漏的情况下,A′为0;当S≠0时,即发生泄漏的情况下,A′会随S和Δpset的增大而不断增大。上述特性与林天翔等[13]的研究结果一致。

图4 水压恒定条件下A′与S之间的关系Fig.4 Relationship between A′ and S under constant water pressure

对比图3,4的仿真结果可以发现:一方面,当Δpset取一定值时,在同样的泄漏孔面积条件下,ΔA′信号会大于A′信号,例如,当Δpset=0.6 MPa时,泄漏孔面积S同样是16 mm2的条件下,ΔA′约为1.1×107N1.6/m2.2,而A′仅约为7.0×106N1.6/m2.2,因此笔者方法通过适当选取Δpset可以获得更强的泄漏信号,这有助于提高检测灵敏度;另一方面,采用恒定水压监测的方法,通常需要水泵根据水压传感器的反馈信号频繁工作,这容易造成水泵的损坏,而在笔者方法中,水泵仅在水压下降到预设最小值时才启动,从而减小了水泵长期频繁工作引起疲劳损坏的概率。

为了进一步讨论Δpset对上述ΔA′相对于A′信号增强程度的影响,根据式(5)和式(8)可以得到信号放大率r的表达式为

(9)

根据式(9),通过仿真得到当p0取不同值时r与Δpset之间的关系,具体情况如图5所示。仿真中:p0分别取0.2,0.3,0.4,0.5,0.6 MPa。由图5可以发现:在一定p0条件下,r随Δpset的增大而增大,并不断逼近3;要使r大于1,Δpset需要大于一定值,且该值随p0的增大而增大,例如,当p0分别为0.2 MPa和0.6 MPa时,Δpset分别需要大于约0.19 MPa和0.55 MPa才能满足r大于1。因此,在实际系统中,可以通过优化p0和Δpset的方法实现监测信号的增强,且笔者方法相较于林天翔等[13]的方法可将信号放大到接近3倍,从而提高监测信号的信噪比。

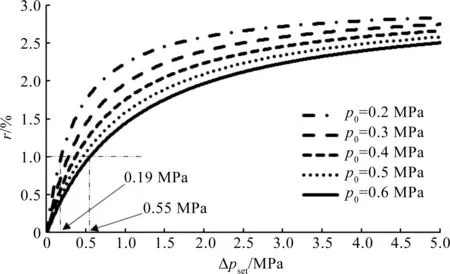
图5 不同p0时r与Δpset之间的关系Fig.5 Relationship between r and Δpset under different p0

3 泄漏监测算法

3.1 算法原理

基于上述振幅信号特性的理论分析结果,可以构建输水管道泄漏的监测算法,具体如图6所示。图6算法包括状态触发模块、振幅算法模块以及泄漏判定模块,该算法可以针对某1个振动传感器的振动信号实现对泄漏的判定。根据图1所示的系统,由于每段输水管对应了1个振动传感器,因此对每个传感器的输出振动信号实施笔者算法可以实现分布式监测,从而确定泄漏点位于哪一段输水管。

图6 泄漏监测算法Fig.6 Algorithm for leakage detection

3.1.1 状态触发算法模块

状态触发算法模块用于发送水泵的工作状态指令。水泵工作状态分为启动前准备、启动加压以及结束加压。

当水泵刚开始进入启动前准备状态时,状态触发算法模块向振幅算法模块和泄漏判定模块发送启动加压准备指令1;当水泵刚进入启动加压状态时,状态触发算法模块向振幅算法模块和泄漏判定模块发送启动加压指令2;当水泵刚进入结束加压状态时,状态触发算法模块向振幅算法模块和泄漏判定模块发送结束加压指令3。将发送指令1和2的时间间隔设定为tp。

3.1.2 振幅算法模块

当收到状态触发算法模块发送的指令1时,振幅算法模块开始对输入的振动信号以Δt作为时间间隔进行采样,并以T作为一个振幅提取周期。在每一个振幅提取周期T中,采用比较法获得采样得到的振动信号的最大值与最小值,并将最大值减去最小值,从而得到每一个周期T的振幅,并将各周期T的振幅进行存储。

当经过时间tp,收到状态触发算法模块发送的指令2时,振幅算法模块停止对振动信号的采样以及每一个周期T的振幅的计算,改为计算在tp时间段中所存储的振幅平均值Av1,并将该值发送给泄漏判定算法模块。

当收到状态触发算法模块发送的指令3时,振幅算法模块又重新开始采样输入的振动信号,同时计算并存储振幅数据(如接收到指令1时的算法);当经过时间tp后,计算存储的振幅平均值Av2,并将该值发送给泄漏判定算法模块。

3.1.3 泄漏判定算法模块

泄漏判定算法模块用于判定泄漏状态。当收到状态触发模块发送的指令1时,泄漏判定算法模块进入准备状态,并对相关寄存器进行清零。当收到振幅算法模块发送的第1个振幅平均值Av1后,将该值存储在寄存器R1中;当收到振幅算法模块发送的第2个振幅平均值Av2后,将该值存储在寄存器R2中。最后计算得到Av1与Av2之差,并与判定阈值Ath进行比较。当两个平均值之差大于或等于Ath时,判定为泄漏;当两个平均值之差小于Ath时,判定为正常。

3.2 算法仿真

为了验证上述算法的效果,通过数值仿真进行验证。实际系统中,振动信号会存在背景噪声[13],为了便于分析,假设背景噪声为正态分布随机信号。仿真中,以水泵刚进入启动前准备状态的时刻作为0时刻,因此归一化振动信号V可以表示为

V=Mv(t)

(10)

(11)

式中:v(t)为均值是0且标准差是1的关于时间t的标准正态分布随机函数;B为振动信号背景噪声的归一化幅度。

根据式(10),不同泄漏孔面积下的归一化振动信号如图7所示。图7(a～h)分别为泄漏孔面积S取18,14,8,5,4,2,1,0 mm2时的振动信号。仿真参数如下:p0=0.3 MPa;pset=0.5 MPa;k=0.005 MPa/s;tp=10 s;B=3×106N1.6/m2.2。图7中:在0～10 s,水泵处于启动前准备状态;在10～50 s,水泵处于启动加压状态;在50～60 s,水泵处于结束加压状态。由图7可知:振动信号幅度总体上随着S的减小而不断减小;在水泵处于启动加压的过程中,振动信号幅度存在不断增大的变化过程,且该过程随着S的减小而变得不明显。

图7 振动信号Fig.7 Vibration signal

采用3.1节所述的算法构建仿真模型对图7的振动信号进行状态判断得到表1所示结果。仿真参数如下:Δt=1 ms;T=100 ms;Ath=3×106N1.6/m2.2。由表1可知:当S≥4 mm2以及无泄漏的情况下,可以得到正确的判定结果;然而,当S=2 mm2和1 mm2时,出现了错误的判定结果。这主要是由于泄漏孔面积减小到一定程度时,根据上述算法得到的振幅在水泵加压前后的改变量会小于判定阈值Ath,因此将泄漏误判为正常。

表1 算法判定结果(Ath=3×106 N1.6/m2.2)

为了提高泄漏判定的准确率,在算法仿真模型中将Ath减小到1.5×106N1.6/m2.2,得到表2所示判定结果。由表2可以发现:判定结果全部正确,因此减小Ath有助于提高泄漏状态下的判定准确率。

表2 算法判定结果(Ath=1.5×106 N1.6/m2.2)

根据上述分析结果,进一步将算法仿真模型中的Ath减小到1.5×105N1.6/m2.2,得到表3所示的判定结果。不同于表2的结果,表3中虽然在泄漏情况下都能得到正确的判定结果,但是在无泄漏的情况下,算法会有一定的误判概率。这主要是因为在无泄漏的情况下存在随机噪声,所以振幅在水泵加压前后的改变量与判定阈值Ath的大小关系具有不确定性。

表3 算法判定结果(Ath=1.5×105 N1.6/m2.2)

根据上述分析结果,Ath过大会引起小面积泄漏孔的漏判;而Ath过小会引起无泄漏情况的误判。因此,在系统中需要根据实际合理设置Ath,以提高判定的准确率。

4 结 论

对水泵启动加压过程中的输水管道泄漏振动信号特性进行了深入研究,提出了利用水泵加压前后振动信号幅度差来监测输水管道泄漏的方法,以提高有用信号的信噪比。理论研究结果表明:相较于已有的利用恒定水压条件下振动信号的技术[13],笔者提出的技术在一定条件下可将泄漏信号强度增大到近3倍。同时,提出了该技术的具体实现算法,仿真分析结果显示:振动信号幅度差判定阈值的合理选取有助于降低对泄漏状态的漏判率以及对非泄漏状态的错判率,笔者所提出的监测技术可有效提升隧道消防输水管道的泄漏检测灵敏度。