多主体市场下的园区综合能源系统随机鲁棒运行优化

2024-01-18周丽红王成山

电力系统自动化 2023年24期

周丽红，于浩，李鹏，王成山

（智能电网教育部重点实验室（天津大学），天津市 300072）

0 引言

园区综合能源系统（park-level integrated energy system，PIES）直接面向终端用户，通过电、气、热、冷等多种能源形式紧密耦合与相互转化，能协调利用外购能源和本地分布式资源，灵活高效地满足用户多类型能源供需，也具有向外部能源系统提供能源输出获利的潜力［1］。因此，PIES 运行将不可避免地受外部能源市场价格波动的影响。特别在配电网售电侧市场改革不断深入的趋势下，微网、虚拟电厂、分布式发电集群、储能电站等多元化市场主体将与PIES 共同参与配电市场交易，从而形成多主体灵活参与的配电网售电市场［2］。在该市场中，除固定价格传统交易模式以外，还可能存在其他形式，如点对点交易［3-4］、博弈议价交易［5］、实时动态交易［6］等，使得市场电价机制呈现多样性、复杂化特征，电价不确定性显著增强［7］。此时，如何克服市场电价不确定性给系统运行经济性带来的不利影响，是PIES 运行优化重点关注的问题之一。

目前，在考虑电价影响的PIES 运行优化研究中，配电网大多采用分时电价［8-9］、尖峰电价［10］等定价模式，但其并不能很好地反映配电网电价在多主体市场中的动态变化特征。而在配电网动态定价方面，近年来围绕博弈定价、协议定价等机制下的PIES 运行优化问题开展了探索，如文献［5］通过构建配电网与微网运营商的合作主从博弈混合模型，优化微网交易电价，实现系统运行成本最优；文献［11］将微网中各用户能量块构建成区块链节点，通过点对点交易生成含能源交易价格的智能交易合约，实现系统运行优化等。但该类研究采用的电价形成机制大多局限于几个特定市场主体，而对于参与主体更加多样的配电市场，个体PIES 对市场价格影响有限，往往只能作为外部价格的接受者，难以采用明确的电价形成机制来指导自身运行。此外，在多主体配电市场中，电力作为一种商品，其价格既具有随机性和波动性特征，同时还需要符合市场公平性要求，这些需求尚未在现有研究中予以充分考虑。因此，为了更好地刻画配电网电价特征，本文将其类比于资产价格，应用几何布朗运动［12］来刻画市场售电价格，并基于市场交易公平性原则，在风险中性测度［13］下建立配电网合理售电价格模型，为PIES运行优化提供指导。

在考虑不确定性的PIES 运行优化方面，相关研究主要关注负荷、可再生能源出力的随机性影响［14-15］，最常采用概率分布和不确定集对不确定性参数进行建模，然后对应地使用随机优化、鲁棒优化方法进行建模求解［16-19］。随机优化［20-21］的本质在于以概率分布有限的场景模拟不确定变量特性，将不确定性问题转化为确定性问题进行求解。该方法用于概率分布函数能准确刻画不确定变量，但对模拟变量规律性刻画和预测精度要求较高的情况不适用，其求解精度依赖于场景模拟数量，计算过程需权衡精度和效率。鲁棒优化［17，22］是基于变量不确定集得到的最恶劣场景最优解，该方法适用于精度要求相对较低、概率分布难以准确刻画、波动范围易获得的不确定变量刻画；但由于考虑了最恶劣场景，往往结果过于保守。为克服随机优化和鲁棒优化的缺点，近年来，有学者将随机鲁棒优化方法引入综合能源系统优化［23-25］，该类研究为本文处理多种不同特征的不确定变量提供了思路。考虑到多主体配电市场中的电能是一种商品，价格虽难以精准预测，但具有围绕理论价格上下波动的特征，其波动范围易得。可再生能源由于其间歇性、波动性和不可预测性，概率分布难以获得，但出力范围容易获得［22，24］；负荷预测精度较高，其波动性或对应的用户用能行为呈现出明显的规律性，可用概率分布刻画［23，26］。因此，本文采用箱型不确定集处理配电网电价和可再生能源出力不确定性，采用蒙特卡洛概率抽样处理负荷不确定性，并采用随机鲁棒优化方法求解，以实现市场价格波动下PIES 优化运行。

1 PIES 系统典型结构

本文以图1 所示典型居民生活PIES 供暖季为例开展研究。其中，PIES 承担园区整体供能和售能任务，可将其表达为一个能源集线器［27］，从外部配电网购入（或售出）电能，从外部气网、热网等购入气、热等常规能源，就地安装光伏、风电等可再生能源，同时配置电、热等储能装置。购入能源经能源集线器传递或转换后，向居民用户提供电、热能源。本文中，配电网价格由市场机制决定并具有不确定性，气、热价格采用固定机制。通过调度系统内分布式能源、储能装置以及用户需求响应等灵活性资源，实现系统在不确定性环境下的经济运行。

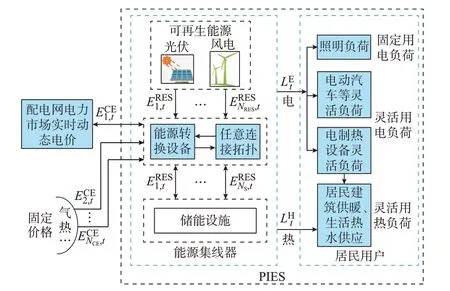
图1 典型居民生活PIES 结构Fig.1 PIES structure of typical residential life

2 基于风险中性测度的配电网合理价格建模

2.1 多主体参与的配电网市场结构

在新型配电网中，除传统的配电网运营商外，在需求侧还含有多个可售电的分布式能源系统，以多样交易方式参与市场竞争，从而形成了多主体参与的配电市场。其中，配电网运营商作为市场内最关键的交易主体，确定其售电合理价格对配电市场交易公平具有重要意义。由于配电网与分布式能源系统的售电竞争关系，配电网售电价格与分布式能源系统售电价格具有相关性。本文中，首先考虑分布式能源售电价格的随机性和波动性，类比资产价格过程，采用几何布朗运动模型刻画其售电价格，得到分布式能源系统售电价格模型；然后，考虑市场公平性基本原则，在风险中性测度下建立配电网售电定价模型，整体思路如图2 所示。

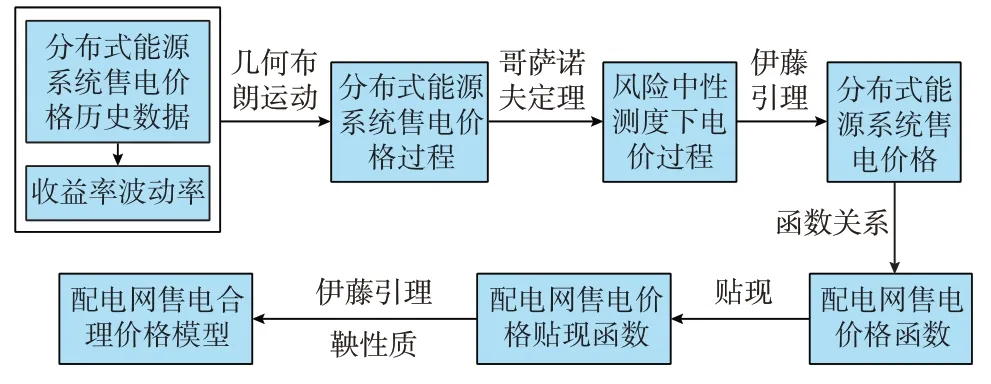
图2 配电网售电合理价格模型构建流程Fig.2 Construction process of reasonable price model for selling electricity in distribution network

2.2 分布式能源系统售电价格模型

经济学中，考虑到几何布朗运动与市场上商品价格运行特征相似性程度较高，故其被广泛用来模拟资产价格［28-31］。类比资产价格过程，配电市场中电力价格始终为正数，其与几何布朗运动的期望相互独立，且运动轨迹与几何布朗运动的轨迹呈现相同的波动性。因此，本文使用几何布朗运动对参与市场竞争的分布式能源系统售电价格进行建模。

设W(t)={W1(t)，W2(t)， … ，WN(t)} (0 ≤t≤T)是概率空间(Ω，F，P)上的多维布朗运动，其中，T为给定的终端时刻；Ω为配电网内N个分布式能源系统售电价格构成的集合，F为Ω上的σ-代数，P为定义在F上的概率测度。

设分布式能源系统售电价格服从概率空间(Ω，F，P)上的几何布朗运动，对于∀i∈{1，2，…，N}，其微分满足：

式中：下标i表示第i个分布式能源系统对应变量；πi(t)为分布式能源系统售电价格；αi(t)为分布式能源系统电价平均收益率，用于描述电价总体趋势变化；σi(t)为分布式能源系统波动率，用于描述电价实时波动。

为刻画分布式能源系统售电价格在风险中性测度P͂下的价格模式，利用哥萨诺夫定理［32］，将真实概率测度P转化为风险中性测度P͂［13］，即

式中：r为无风险收益率；(t)为风险中性测度下的布朗运动。

式（2）的推导过程详见附录A。应用伊藤引理［33］求解式（2），得到分布式能源系统售电价格模型：

式中：πi(0)为分布式能源系统售电价格初值。

2.3 配电网售电合理定价模型

为体现市场交易公平性，分布式能源系统或者配电网运营商若想获得更高收益，需承担更大风险，对电力定价提出了风险补偿要求。在经济学中，只要该商品市场是有效市场［34］，一旦价格偏离合理价格，就有投资者进行无风险套利［35］，从而使风险补偿消失，为保证市场公平性，在对商品进行定价时须假定风险中性［13］。因此，考虑到电力的商品属性，基于风险中性的电力定价即为配电网运营商售电合理价格，简称配电网售电合理电价。

由于配电网运营商售电价格受到参与市场竞争的分布式能源系统售电价格的影响，则设

式中：f(·)为配电网售电价格与分布式能源系统售电价格之间的函数；π(t)为配电网运营商售电价格。

设配电网运营商售电价格贴现过程函数为：

在风险中性测度P͂下，配电网运营商售电价格贴现过程exp(-rt)f是一个鞅［36］，可得到配电网合理售电价格满足的随机偏微分方程：

式中：ρij为第i个与第j个分布式能源系统售电价格相关系数。该随机偏微分方程可采用有限差分法［37］进行求解。式（6）的推导过程详见附录B。

3 考虑电价不确定性的随机鲁棒建模

3.1 PIES 运行优化问题建模

3.1.1 目标函数

为实现系统整体经济运行最优化目标，考虑外购能源成本和二氧化碳排放成本，目标函数如下：

式中：C为能源消耗及其二氧化碳排放费用；下标l为输入能源系统的能源种类对应的变量；E为消耗的常规能源大小；π为常规能源价格；π为除电以外的其他能源二氧化碳排放价格；E为消耗的可再生能源大小；π为可再生能源价格；ΩCE为所有输入系统的常规能源种类集合；ΩRES为所有输入系统的可再生能源集合。

3.1.2 约束条件

图1 中PIES 由能源集线器和居民负荷组成，其优化建模参考文献［38］。同时，为简化能源集线器模型，本文将PIES 内可再生能源与储能视为能源输入变量，得到能源输入与输出关系约束为［27］：

其中

式中：L为能源集线器输出的电、热负荷向量；E为决策变量向量，表示输入能源集线器的能源，包括常规能源、可再生能源和储能，对应的NCE、NRES、NS分别表示其种类数量；E为第1 个常规能源功率；E为第1 个可再生能源功率；E为第1 个输入能源集线器的储能功率；EES，min、EES，max分别为输入能源允许的最小值和最大值向量，与能源集线器内部设施允许的最小值和最大值有关［27］；为能源集线器转换矩阵，与能源集线器内部的分派因子和内部设备转换效率有关［27］；E为第ω个储能装置在τ时刻的功率向量；Q、Q分别为系统内第ω个储能装置允许容量的最小值和最大值向量；和分别为能源集线器输出的电负荷和热负荷。

居民热负荷主要为建筑供暖和生活热水，考虑其热惯性下的灵活性特征，模型可表达为［38］：

式中：下标n为第n户居民用户；为源自能源集线器的热能向量；Un，t为能源输入向量，其中决策变量包括能源集线器向居民输送的热功率、用户自备热泵产生的热功率，非决策变量包括用户行为和太阳能辐射增益、室外温度、热水罐热水负荷等［38］；U、U分别为能源输入向量允许的最小值和最大值；Tn，t为状态变量向量，包括室内温度、储热装置温度等［38］，T、T分别为其允许的最小值和最大值；An和Bn为用户状态空间系数矩阵。

居民电负荷包括固定电负荷和灵活电负荷。固定电负荷为照明等不具有需求响应能力的负荷，灵活电负荷包括冰箱、洗衣机、电动汽车等可转移的灵活性电负荷。参考文献［38］，可转移的灵活性电负荷可用可调负荷模型进行表达，即

3.2 考虑不确定性的PIES 随机鲁棒优化模型

在负荷不确定方面，本文主要考虑室内温度区间的随机设定以及用户热水负荷随机性两方面因素，采用蒙特卡洛方法进行模拟。室内温度随机设定与式（13）变量T、T相关；热水负荷模拟与式（10）—式（12）变量Un，t中的热水罐负荷相关。

在新能源出力和电价不确定性方面，本文通过引进不确定调节参数，构建箱式不确定集刻画其随机性特征，对于∀l，t，有

式中：π、ES，max分别为配电网电价和可再生能源功率的不确定变量；分别为配电网合理电价和可再生能源功率预测值；αCE、αRES分别为配电网售电价格和可再生能源功率允许波动的最大偏差率；Δπ、ΔE分别为配电网售电价格和可再生能源功率的单位波动偏差；ΓE、ΓRES分别为配电网实际电价和可再生能源功率的不确定调节参数；V1、V2分别为配电网实时电价和可再生能源功率的箱型不确定集。

在式（17）和式（18）的基础上，将式（7）转化为如下随机鲁棒优化模型：

式（19）表明，在考虑配电网售电价格和可再生能源功率的不确定集合后，模型由单阶段转化为两阶段模型，约束条件为式（8）—式（18）。为简化表达，给出该模型的紧凑形式，即

4 模型求解

本文随机鲁棒优化模型将原优化模型拆分为主问题和子问题。主问题是在配电网售电价格和可再生能源负荷最恶劣情况下，得到最优方案，进而确定随机部分最优值；子问题是在得到主问题最优方案下，随机部分目标函数根据得到的已知优化变量，设置不确定参数ΓE和ΓRES，得到使子问题目标函数最大的配电网售电价格和可再生能源最恶劣场景，以及其反映随机部分的最优值；最后，通过迭代直至主问题和子问题分别得到的随机部分最优值之差收敛，则找到最优解。

采用列与约束生成算法［39］求解上述两阶段随机鲁棒优化模型，可将原问题式（20）分解为主问题和子问题，其中主问题具体形式为：

式中：ψ为随机变量已知条件下的随机部分；h(p)为第p次迭代时的变量；v、v分别为第p次迭代后得到的最恶劣情况下不确定变量v1、v2的取值；pmax为迭代次数的最大值。

子问题具体形式为：

在给定一组z=z*的已知情况下，不确定变量v1、v2取得边界值时，式（22）取得最大值［17］。即系统在T时段内，当PIES 向配电网售出电能时，配电网售电价格达到最低；当PIES 向配电网购入电能时，配电网售电价格达到最高且可再生能源功率取得最小值，此时系统运行成本最高，即为最恶劣场景。因此，对于∀l，t，可将式（17）、式（18）改写为如下形式：

式中：k1，t为t时刻目标函数系数向量，其中k1=为t时刻优化变量zt的给定和分别为配电网实际电价和可再生能源功率的实时不确定参数值。

在给定一组z=z*的已知情况下，求极小问题可以转化为求对偶极大问题，故子问题可转化为：值，其中

式中：ζ1、ζ2为子问题对偶变量。

上述变换将两阶段随机鲁棒问题转化为主问题式（21）和子问题式（25），使用列与约束生成算法求解，流程如下：

步骤1：给定一组最恶劣的场景v1、v2作为初始的最恶劣场景，设定子问题运行成本的上界UB和下界LB，迭代次数p=1。

步骤2：根据步骤1 给定的最恶劣场景v、v，应用式（21），参考文献［38］求解主问题，得到最优解和，并将作为新的下界，即LB=max(LB，)。

步骤3：将主问题的解代入子问题，应用式（25），得到子问题的最优解fp()和新的最恶劣场景 (v，v)*，更新成本上界为UB=min(UB，fp())。

步骤4：若UB-LB≤ε（ε为设定的收敛阈值），则表明已求得最优解，停止迭代；否则更新变量及约束和

步骤5：令p=p+1，，返回步骤2，直至收敛。

5 算例分析

5.1 算例设置

本文算例中，假设共有1 个配电网运营商和3 个分布式能源系统A、B、C 构成配电市场，算例以典型日为例进行研究，详见附录C。PIES 中，供给侧包括4 种输入能源：上级电网电力、上级气网天然气、就地光伏发电、就地电储能；能源集线器内含有变压器、电储能、光伏、热电联供机组，具体算例模型参照文献［38］。算例中，灵活性电负荷预测值为固定负荷功率的30%，其最小值和最大值分别取其预测功率的50%和150%，固定电负荷详见图C1；除变压器和光伏装机容量分别为20 000 kW 和18.4 MW，光伏能源价格为0.1 元/（kW·h），需求侧含512 户居民用户，光伏出力预测功率详见图C1的参数和数据变更以外，其他相关参数均参考文献［38］。算例以典型日为例进行研究，系统调度周期为一天（96 个时段），调度间隔为15 min。

本文对居民负荷随机性采用蒙特卡洛模拟，设配电网售电价格单位波动偏差为0.02 元/（kW·h），可再生能源功率单位波动偏差为1 000 kW；在MATLAB 2016b 环境下编程求解，计算结果为100 次模拟的均值。

5.2 多主体市场电价特征建模必要性分析

为验证多主体市场电价建模对PIES 运行优化的必要性，本节设配电网实际电价和可再生能源功率的不确定性调节参数均为0，分析配电市场分布式能源系统售电价格波动和系统间相关性对配电网合理售电价格的影响。本文以附录C 算例为参照，分布式能源系统售电价格波动率σ分别取0.1、0.5、1.0、1.5，其他参数不变，得到配电网合理售电价格及PIES 运行优化结果，如图3 和表1 所示。

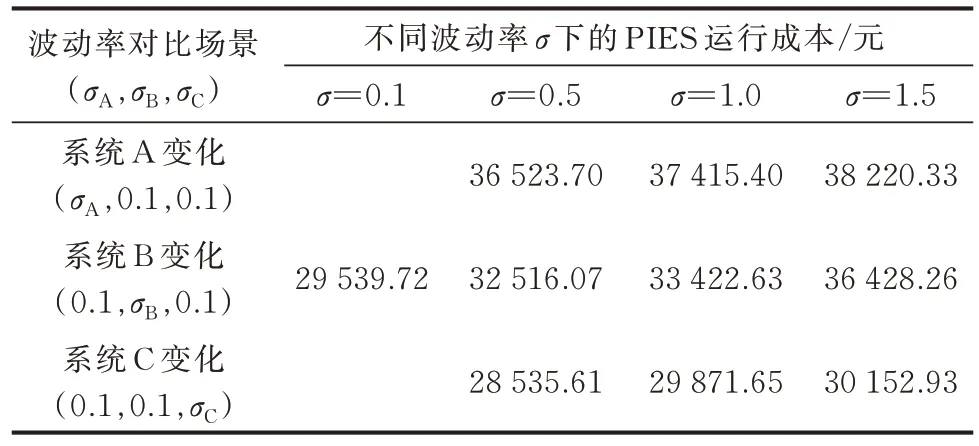
表1 分布式能源系统不同波动率下PIES 日前优化结果Table 1 Day-ahead optimization results of PIES with different volatility rates of distributed energy systems

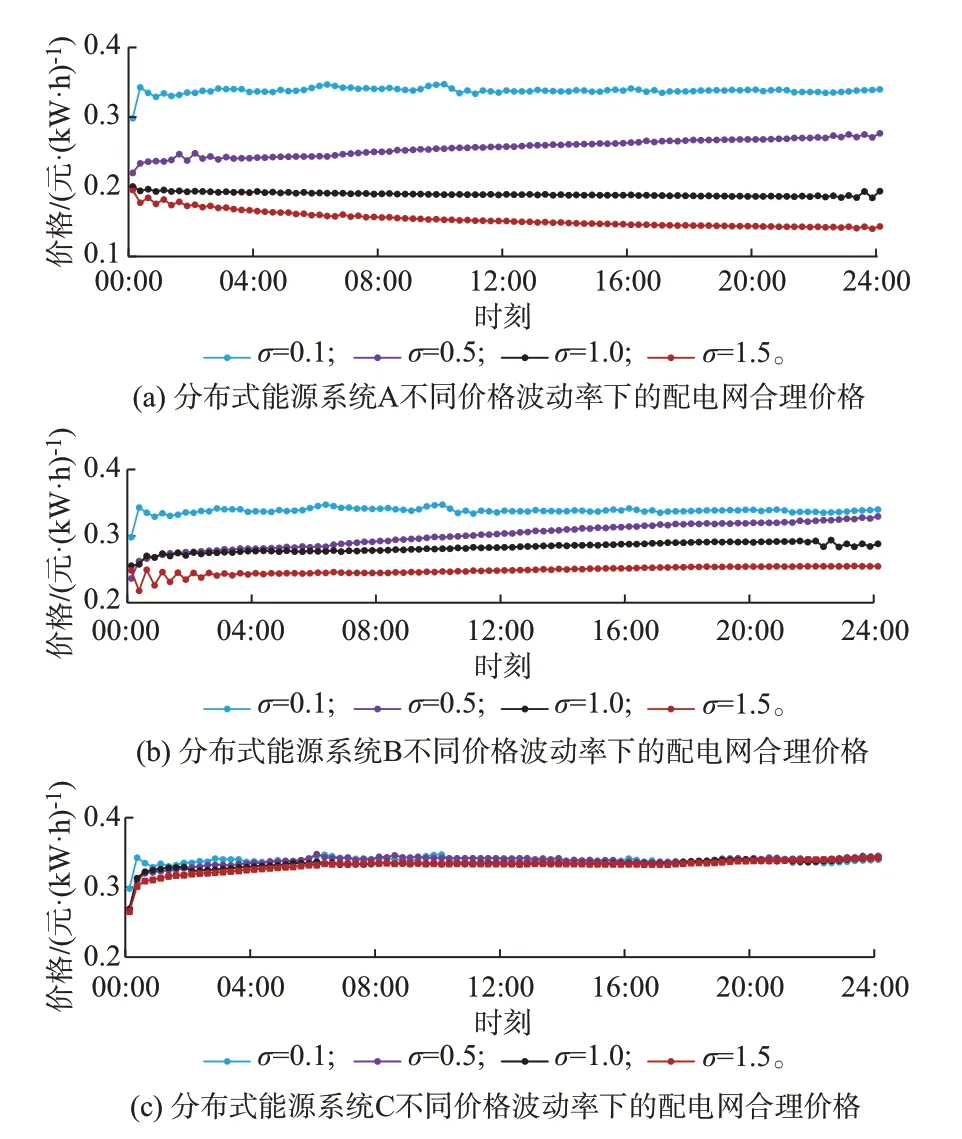
图3 售电价格波动性对配电网合理电价的影响Fig.3 Influence of selling electricity price volatility on reasonable electricity price of distribution network

结果表明，售电价格期望较高的系统A 和B，随着波动率增大，配电网售电合理价格明显下降，PIES 运行成本有不同程度的增加，如系统A 波动率σA=0.1 与σA=1.5 比较，运行成本增加了29.39%，系统B 波动率σB=0.1 与σB=1.5 比较，运行成本增加了23.32%。结合附录C 图C3 系统A 结果可知，相比波动率为0.1 的场景，波动率为1.5 的场景在运行策略上PIES 卖出电能变化很小，而买进电能和天然气有不同程度的变化。总体上看，合理的价格下降使得PIES 获益急剧下降，买进能源总量成本变化并未抵消售电损失，致使PIES 成本呈现较大幅度上升。而对于售电价格期望较低的系统C，其波动率σC变化对售电合理价格影响较小，从而对PIES 运行成本影响不大。

配电网售电合理价格还受分布式能源系统间售电价格相关系数影响。本文以附录C 算例为参照，设分布式能源系统A、B、C 的售电价格相关性分别处于负相关、不相关、正相关、完全正相关，相关系数ρ分别取-0.5、0、0.5、1.0，其他参数不变，得到PIES运行成本分别为29 059.87、30 098.49、26 665.90、30 037.61 元，配电网合理售电价格如图4 所示。

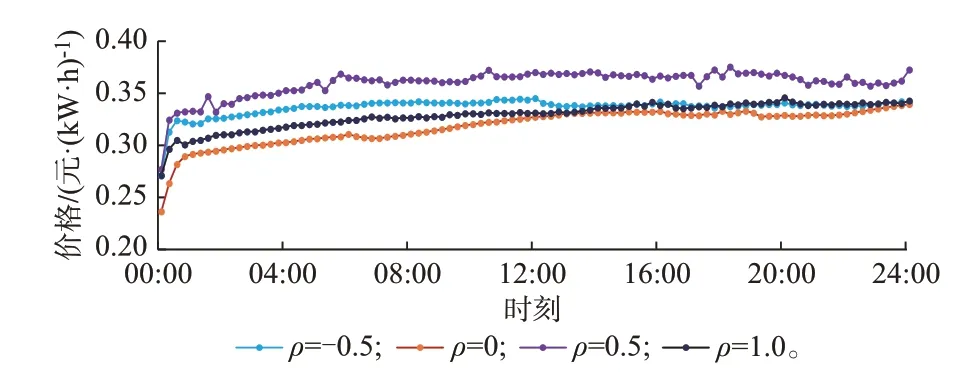
图4 售电价格相关性对配电网合理电价的影响Fig.4 Influence of selling electricity price correlation on reasonable electricity price of distribution network

结果表明，分布式能源系统间相关性强弱会使得配电网合理电价以及接入市场的PIES 运行成本发生变化。结合附录C 图C3 可知，相比相关系数为0 的分布式能源系统互不相关场景，相关性为1 的场景的运行策略呈现出不同结果。

由上述分析可知，在配电市场条件下，分布式能源系统售电价格波动率、相关系数等价格特征变化会对配电网合理价格产生不同程度的影响，从而影响PIES 运行优化结果。而传统的固定电价、尖峰电价等方式不能充分考虑市场实时变化，表明本文提出的采用合理定价模型刻画市场特征，并进一步将其考虑到PIES 运行优化中具有必要性。

5.3 随机鲁棒运行优化与传统方法的对比分析

为验证本文随机鲁棒优化方法处理不确定问题的优点，将结果与随机优化和鲁棒优化方法运行结果进行比较。采用控制变量法，将不确定性变量视为实验变量，其余条件均与算例初始设置一致。

本文随机鲁棒优化采用箱型不确定集刻画电价和光伏出力，其允许波动的最大偏差率均为30%，不确定调节参数取其所钳制的最大调节参数分别为ΓE=471.48、ΓRES=392.13；蒙特卡洛随机模拟用户行为的负荷不确定性，具体设置参考文献［38］。

随机优化方法中，设电价和光伏出力不确定性均服从正态分布，期望分别为合理电价、光伏预测出力，两者置信度均为99%且其允许偏差率为±30%以内，采用蒙特卡洛模拟该场景；负荷不确定性具体设置与随机鲁棒优化场景相同。

鲁棒优化方法中，箱型不确定集刻画电价和光伏出力，具体设置与随机鲁棒优化场景相同；负荷不确定性采用盒式不确定集，设电、热总负荷预测值为随机鲁棒优化场景下随机概率模拟负荷均值，允许波动偏差率为±30%以内。

随机鲁棒优化、鲁棒优化和随机优化方法下，PIES 日前运行成本分别为82 037.72、93 034.75、29 173.24 元。随机鲁棒优化方法较鲁棒优化方法运行成本低11.82%，这是因后者考虑了负荷、电价和光伏出力3 种不确定参数最恶劣场景，而前者仅考虑电价和光伏出力两种不确定参数最恶劣场景，使得随机鲁棒优化结果较鲁棒优化结果进取。此外，与鲁棒优化相比，随机鲁棒优化的负荷需随机模拟多场景，使得其耗时更长。

随机鲁棒优化方法比随机优化方法运行成本高181.21%，这是因为前3 种不确定参数中的2 种考虑了最恶劣场景，而后者全部采用随机场景模拟，随机鲁棒优化方法带有一定的保守性，导致其相较随机优化运行成本更高。此外，由附录C 图C4 可知，随机鲁棒优化较随机优化箱体长度更短，反映其结果更容易收敛且耗时更短。

由以上分析可知，随机鲁棒优化根据不同不确定参数特点，融合了随机优化和鲁棒优化的优点，相较于随机优化方法计算高效但策略保守，相较于鲁棒优化计算速度较慢但策略进取。实际工程中，不确定参数种类较多且具有不同特征，使得随机鲁棒优化较传统方法实用性更强。

此外，本文所提随机鲁棒优化还具有一定的灵活性，如附录C 图C5 所示，对比不确定参数对系统运行成本的影响。结果表明，随着不确定调节参数增大，系统运行成本也在提高，这是因为当系统更多地考虑不确定性时，需牺牲经济性来满足运行鲁棒性。因此，用户可灵活地调节不确定参数，得到兼顾经济性和鲁棒性的运行优化策略。

5.4 多主体市场电价不确定性对运行结果的影响

为验证市场电价不确定性对运行结果的影响，设光伏出力允许波动最大偏差率αRES=30%和不确定调节参数ΓRES=20，对比电价允许波动最大偏差率αCE和不确定调节参数ΓE变化对系统运行结果的影响，如图5、附录C 图C6 和图C7 所示。图5 中，ΓE，max为仅考虑αCE时系统随机鲁棒运行对应的可调参数，为ΓE最大值。

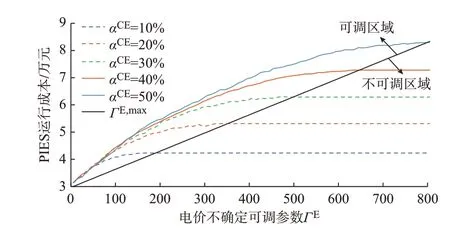
图5 电价不同不确定参数下的PIES 日前运行优化成本Fig.5 Optimal costs of day-ahead operation for PIES with different uncertain parameters of electricity prices

结果表明，αCE不变，当0 ≤ΓE≤ΓE，max时，随着ΓE参数增大，系统运行成本增加。以αCE=30%、ΓE为0或200、ΓE，max=471.48 为例，相比ΓE=0，即电价确定的场景，可调参数分别为200 和ΓE，max时，PIES 运行成本分别增加71.40%、101.27%。结合附录C 图C6 可知，系统电、气和光伏用能策略均发生较大变化；当ΓE≥ΓE，max时，因其受αCE钳制，使得最恶劣条件下选择场景范围与ΓE，max一致，导致其系统运行结果与ΓE，max相同。由此可知，0 ≤ΓE≤ΓE，max为ΓE参数可调区域；ΓE≥ΓE，max为ΓE参数不可调区域，图5 中黑色直线为可调区域和不可调区域分界线。ΓE不变，当αCE增大时，系统运行成本增加。以ΓE=200，αCE取0、20%、50% 为例，随着电价允许偏差率增大，相比αCE=0 的电价确定场景，电价允许最大偏差率分别为20%和50%时，PIES运行成本分别增加61.51%、75.22%，结合附录C 图C7 可知，系统用能策略也发生较大变化。

因此，市场电价不确定增大，即反映单位电价不确定波动幅值大小αCE和在可调区域内反映波动总幅值大小ΓE增加，使得最恶劣条件下场景选择范围增大，为保证系统鲁棒性，将导致系统运行成本增加和运行策略发生较大变化。说明电价不确定性越大，运行成本越高，系统运行策略也会相应呈现不同结果。