基于暂态特征分布的单端量后备保护自适应配合方案
2024-01-18常娜娜宋国兵常仲学张晨浩郑玉平吴通华
常娜娜,宋国兵,常仲学,张晨浩,郑玉平,吴通华
(1.西安交通大学电气工程学院,陕西省西安市 710049;2.南瑞集团有限公司(国网电力科学研究院有限公司),江苏省南京市 211106;3.电网运行风险防御技术与装备全国重点实验室,江苏省南京市 211106)
0 引言
以新能源为主体的新型电力系统,具备新能源大规模并网、新型储能、可调节负荷广泛接入等特征[1-2]。与传统电力系统相比,新型电力系统包含了大量的电力电子设备,网络形态发生了本质变化。电力电子器件的脆弱性和控制策略的复杂性,导致适用于传统交流电网的阶段式配合的过流保护无法满足新型电力系统的保护需求[3-4]。电网结构日趋复杂导致基于固定时延的单端量后备保护整定工作量大;新能源接入的随机性、运行方式的多样性导致其整定困难,失去选择性的情况时有发生[5-7]。因此,亟须研究适用于新型电力系统的无需逐级整定的单端量后备保护方案。
针对高比例新能源规模化或集群化并入配电网的情形,国内外在保护配合方面进行了大量研究[8-14]。文献[8]为解决逆变类分布式电源(inverterinterfaced distributed generation,IIDG)接入及配电网运行方式变化给传统电流保护带来的难题,提出了一种计及量测数据缺失及错误的配电网电流保护自适应整定方法。文献[9]提出一种适用于分布式电源(distributed generator,DG)的自适应多级定时限过电流保护方案,主、后备保护的协调方案可同时满足选择性和灵敏性要求。但当阶段式电流保护主保护拒动时,靠近电源侧的后备保护动作时间较长,后备保护动作性能欠佳[10]。文献[11]提出一种计及后备保护优化级数的改进阻抗修正反时限过流保护整定方法;文献[12-13]引入双重设置或双重化配置过流继电器的方案应对DG 接入或网络拓扑变化时的保护配合问题;尽管反时限过流继电器具有自动反映故障严重程度的能力,但所提方法整定工作量仍非常大。文献[14]提出了一种基于统一反时限特性方程的故障识别方法,为简化整定计算提供了思路。
但高比例新能源集群化接入使得基于稳态量的保护灵敏度下降,如文献[15]阐述了大规模风电接入电网的继电保护问题,风电场在线路故障后向电网持续提供短路电流的能力差,导致并网点联络线保护拒动;文献[16]表明换流器脆弱性约束下的高可控性导致短路电流受限,应研究面向被保护对象的时域保护方法。初始行波的故障特征仅与网络拓扑有关,不受控制策略影响,但对采样率要求太高[17]。暂态量保护充分利用不同频带下暂态信号的特征实现故障判别,其反映电网自身的暂态特性,不受系统电源种类与容量影响[18]。因此,以不受调节特性影响的继电保护新原理为目标,研究利用暂态信息进行故障判别、稳态信息进行故障确认的接力式后备保护方案是很有必要的。
本文定性分析了分布参数模型下故障分量瞬时实功率的暂态频谱特征,利用阻抗特性验证不同拓扑结构下其随频率变化的分布规律,依据固定拓扑得出具有自然分布特征的最小适用频带,计算时域暂态能量。将暂态能量与用户自定义的反时限特性方程结合得到全网统一方程的排序函数,由其计算的动作时间和稳态判据共同构成自适应故障严重程度的单端量后备保护方案。仿真验证了所提方案的正确性。
1 已有阶段式配合的后备保护适应性分析
图1 给出DG 接入配电网的不同场景,用于分析已有阶段式配合的过流保护和反时限保护的适应性。图中:S 为系统电源;L1~L3为线路L1~L3 的长度;x为L2 上故障点f1与母线B间的距离;LbA1、LbAn和LbB1、LbBn分 别 为 母 线A、B上 对 应 分 支线 的 长 度;LdA1、LdAn和LdB1分 别 为 对 应 的 负 荷;R1~R6为保护。
图1(a)中,R1的过流Ⅲ段用作R2的远后备。发生f1故障时,DG 的外汲作用导致流过R1的故障电流减小,当其小于R1过流Ⅲ段定值IⅢ1,set时,会出现主保护拒动、R1无法起到后备保护功能的情况。忽略负荷电流的影响,R1、R2失配时的动作方程为:
式中:ES、ZS分别为系统额定电压、等效阻抗;z1为线路单位长度阻抗;IDG为DG 输出的故障稳态电流。
由式(1)得R1、R2失配时的IDG满足式(2)。
当IDG或L1变化使得式(2)成立时,传统三段式过流保护会出现配合问题。
图1(b)中,f1故障时,DG 提供故障电流的弱馈性使得流过R6、R4的故障电流非常小,导致相邻两级保护间的正序故障分量电压差异也非常小。因此,无法利用网络拓扑中正序故障分量电压的自然差异得到文献[14]中基于统一特性方程的反时限后备保护,也就无法实现无需逐级整定的自适应配合。
综上,针对已有阶段式配合的后备保护在高比例DG 接入后存在失配和难以简化整定的问题,需研究新的保护方案以适应DG 随机接入的场景。
2 故障分量瞬时实功率的暂态分布特征
以图1(a)含有2 级线路的简单网络为例分析故障分量瞬时实功率的暂态分布特征。
时域中,Rj的故障分量瞬时实功率Δpj等于本地测量的1 模和2 模的电压、电流故障分量的乘积之和[19],其表达式为:
式中:j为保护编号;Δu1m,j、Δi1m,j分别为1 模电压、电流故障分量;Δu2m,j、Δi2m,j分别为2 模电压、电流故障分量。
根据时频域卷积定理[20]可得,式(3)的频域表达式为:
式中:P、U和I分别为频域的相应功率、电压和电流;ω为角频率;“*”为卷积。
由于1 模和2 模网络相同[21],本章的理论分析不区分1 模和2 模。
2.1 不同保护安装处的暂态频谱特征
保护需求不同,元件采用的等效模型不同。频率高达几千赫兹以上的暂态研究中,变压器须采用频率相关模型,并考虑电容的影响[22]。暂态量保护中,母线系统为波阻抗不连续点,母线本身和变压器对地电容可等效为一常数[23]。配电变压器的感抗很大,则经它接入的负荷可认为处于开路状态[24]。DG 大都需要通过逆变器并网,而逆变器的波阻抗也非常大,则经它接入的DG 也相当于处于开路状态[25]。
当线路采用频变参数模型时,图1(a)中f1故障时的线模故障分量网络如图2 所示。 图中:ΔUmj、ΔImj分 别 为Rj的 线 模 故 障 分 量 电 压、电 流;ΔIm1L为点1L处的线模故障分量电流;Uf、If分别为故障点等效电压、电流;RL1、LL1、CL1和RL2、LL2、CL2分别为单位长度的电阻、电感、电容;C1、C2为母线等效电容;RMn、LMn、CMn分别为母线M(A或B)上第n条分支线单位长度的电阻、电感、电容;CbMn为母线M上第n条分支线上变压器等效电容;ZA、ZB分别为由点1 或点2 看入的所有分支线的等效阻抗。
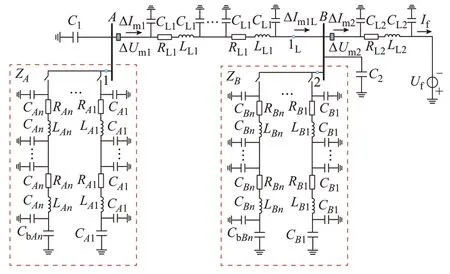
图2 线模故障分量网络Fig.2 Line mode fault component network
文献[26]中定义Rj的电压、电流与故障点等效电压的比值分别为对应的电压系数KUj、电流系数KIj,即
结合式(4),本文定义Rj的功率系数KPj为:
它表示故障分量功率在网络上的传输特性。
由分布参数模型可得f1与R2、R1间的电压、电流关系为:
式中:ZC1、ZC2和γ1、γ2分别为线路L1、L2 的波阻抗和传播系数。
由节点电压、电流关系得:
式中:Z2eq、Z1eq分别为R2、R1向左看入的等效阻抗。
联立式(6)至式(8)得:
其中
式中:Zeq1L为从点1L向左看入的等效阻抗;Zs1、Zs2分别为母线A、B上所有分支线阻抗与母线等效电容的 并 联 阻 抗;ZMn、ZCMn、γMn分 别 为M上 第n条 分 支线的等效阻抗、波阻抗和传播系数。
考虑双曲函数的非线性性质,结合母线A、B上没有分支或接入分支时对应的不同拓扑,定性分析功率系数KP的分布特征。图3 给出不同网络拓扑下|KP|的暂态频谱,频段取为1~10 kHz。拓扑1 表示母线A、B上均无分支,拓扑2 表示母线A上有分支、母线B上无分支,拓扑3 表示母线A上无分支、B上有分支,拓扑4 表示母线A、B上均有分支。其中,L1=30 km,x=50 km,C1=0.05 μF,C2=0.01 μF,LbMn=10 km,CMn=0.005 μF,线路波阻抗和对应的传播系数由PSCAD 中线路参数经矢量拟合得到[27]。
由图3 可知,拓扑1 至拓扑4 中,当频率f分别低于 红 色 虚 线 对 应 的fT1、fT2、fT3、fT4时,4 种 拓 扑 下 的|KP2|均是位于|KP1|上方的。也就是说,当频率低于某一值时,任一拓扑下相邻两级保护的|KP|都具有满足距故障点越近、值越大的自然分布特征。且|KP|的分布特征由Z1eq、Z2eq决定,而它们的阻抗特性随拓扑变化而不同。
2.2 阻抗特性验证|KP|分布特征
附 录A 图A1 表 明,Z1eq、Zeq1L、Zs2、Z2eq的 阻 抗特性随着频率增加交替呈现容性或感性,但最低频段仍是容性的[28-29]。利用这一阻抗特性,将各条线路分别等效为随频率变化的集中电容或电感时,得到如图4 所示的等值电路。图中:ZL1为线路等效阻抗;Zx为母线B到故障点的等效阻抗。此时,Z1eq、Zeq1L、Zs2、Z2eq为 固 定 频 段 下 对 应 的 等 效阻抗。
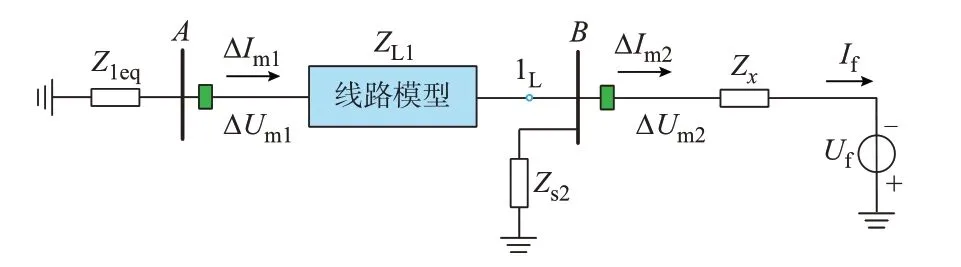
图4 图2 的等值电路Fig.4 Equivalent circuit of Fig.2
取电流参考方向时,由电路理论可得:
由式(5)得:
不同频率下的电压、电流系数分别可展开写为:
式中:ω1、ω2、ωi1、ωi2表示不同的角频率,下标i1、i2表示对应的编号。
由卷积定理得:
由式(14)可知,相邻两级保护|KP|是否存在差异与Z1eq、Z2eq有关,即与拓扑结构密切相关。对于任 意 频 率ωi1、ωi2,KI2(ωi1)KU2(ωi2) 与KI1(ωi1)KU1(ωi2)的差异体现在式(15)中。
式 中:den(ωi1,ωi2) 为 求 取Zeq1L(ωi1)Zeq1L(ωi2) 和Zs2(ωi1)ZL1(ωi2)的和。
当ωi1、ωi2均位于Z1eq、Zeq1L、ZL1、Zs2、Z2eq呈容性的 最 低 频 段,忽 略 电 阻 影 响 时,den(ωi1,ωi2) 和Zs2(ωi1)Z1eq(ωi2)都是负的实数,因此有
又由式(12)可知,最低频段的KI2(ωi1)KU2(ωi2)也是负的实数,则对于固定频率ωi1、ωi2,有
因此,Z1eq、Zeq1L、Zs2、Z2eq、Zx都呈容性的最低频段内,由式(14)可知|KP2|恒大于|KP1|。
随着频率增大,Zeq1L、ZL1、Zx中的任一个呈感性后,会 出 现Zeq1L(ωi1)Zeq1L(ωi2)、Zs2(ωi1)ZL1(ωi2)或KI2(ωi1)KU2(ωi2)为正的情况,导致:
此时,会出现|KP2|小于等于|KP1|的情况,破坏原有的自然分布特征。
因此,阻抗特性验证了|KP|在某一低频段内是有自然分布特征的。该频段的选取由Z1eq、Z2eq、ZL1、Zx共 同 决 定,也 可 表 示 成 式(9)中 的Z1eq、Z2eq、L1、x。
2.3 有自然分布特征的最小适用频带及影响因素
针对某一固定拓扑,Z1eq、Z2eq、L1是已知的,仅反映故障位置的x是未知的。本文将|KPj|从最低频开始逐点累加,加和值记为Hj。比较相邻保护Hj的大小得出最小适用频带的最高频率fmax,则最小适用频带为[0,fmax],其判别公式如式(19)所示。
式中:num为采样点序号;Num为参与加和的频点个数;fNum为KPj(Num)对应的频率。
图5 给出Num增加即累加频率逐渐增加时拓扑2 和拓扑4 对应的加和值H的变化情况。图5(a)表明num从1 开始时,拓扑2 大于fmax的频段不再有自然分布特征;但对比图5(a)和图3(b)可知,当num从大于fmax的某个频点开始时,某一频段仍有可能有自然分布特征。而图5 说明由式(19)得到的有自然分布特征的适用频带是最小适用频带。所选频率应小于采样频率的一半,fmax越小,所需的采样频率越低,因此,采用最小适用频带可以降低测量环节对采样频率的要求。
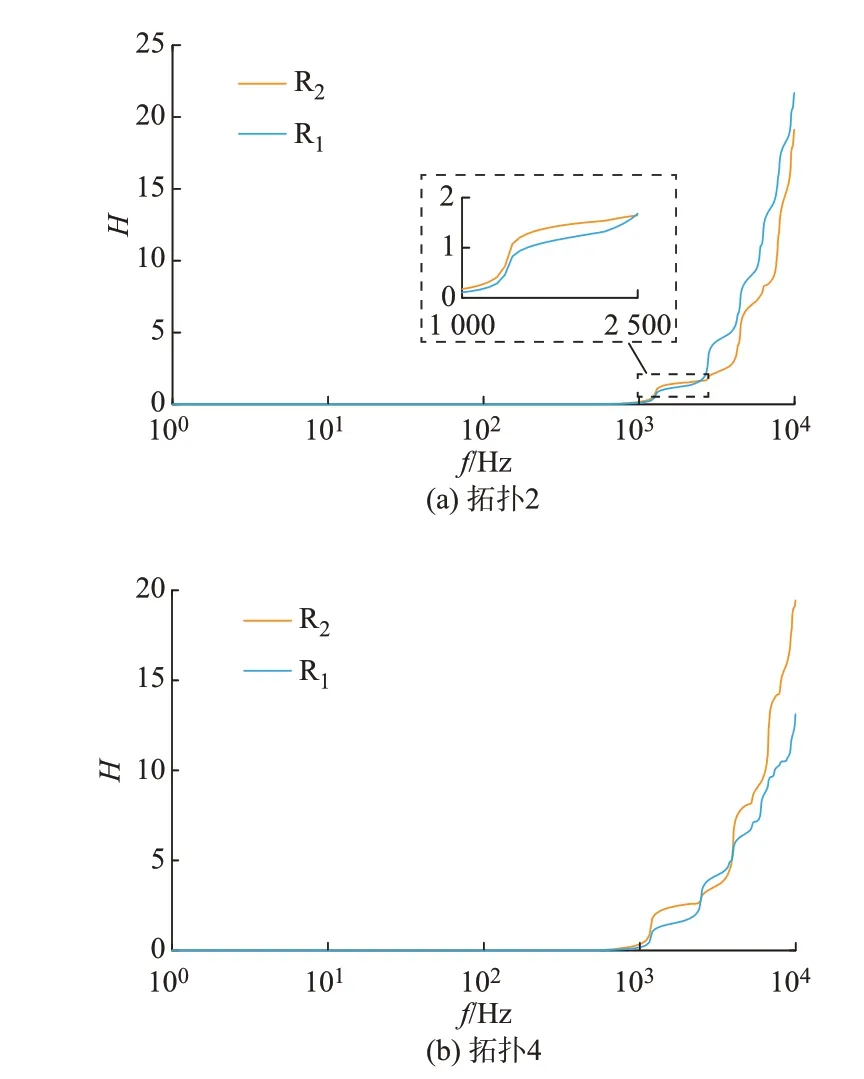
图5 拓扑2 和拓扑4 对应的H 值Fig.5 Value of H corresponding to topologies 2 and 4
不同网络拓扑下fmax与L1、x的对应关系见附录B 图B1。附录B 还分析了线路参数误差对频带选取的影响。
考虑拓扑结构和x对频带选取的影响,本文需依据固定的拓扑和参数离线得到满足自然分布特征的适用频带。
2.4 暂态能量差异
由时频对应关系知,最小适用频带下相邻两级保护时域内的Δpj也是有自然差异的。时域分析须考虑数据窗的选取问题,所选数据窗越长,信号抗干扰能力越强[30];但所选数据窗内换流器一旦进入动态调节阶段,非线性电力电子器件使得网络变得非线性,导致无法使用叠加定理。
电力电子设备控制系统存在的响应延时一般为毫秒级[17]。故障后功率不平衡检测需要一定的时间,因此,调整从直流侧注入的功率会有不可避免的时间延迟(通常超过半个工频周期)[31-32]。因此,换流器动态调节前的时间长度是大于10 ms 的。本文选取故障后换流器响应前的3 ms 数据得到最小适用频带内的时域信息。
利用低通滤波器得到[0,fmax]范围内的Δpj,并由式(20)计算保护启动后3 ms 内的暂态能量Ej,有
式中:Num1为3 ms 内总的采样点数。
由于Δpj具有自然分布特征,则相邻保护的暂态能量Ej也是有自然差异的。不同故障类型下Δpj初始值Δp0的取值情况见附录C 表C1。因此,受故障工况(故障初始时刻、故障类型、过渡电阻、故障位置)影响,Δpj、Ej取值范围都非常广。
综上,故障分量瞬时实功率的暂态特征为:
1)暂态频谱在某一低频段具有自然分布特征,且适用频带与网络拓扑密切相关;
2)依据网络拓扑计算的最小适用频带,在保证自然差异的同时可降低暂态保护对采样率的要求;
3)网络拓扑使得暂态能量在相邻保护中存在自然差异,这为实现无需逐级整定的单端量后备保护自适应配合方案提供了理论基础。
3 基于暂态能量差异的故障识别
3.1 实现思路
反时限特性具有距故障点越近、动作时间越短的特点,故将暂态能量的自然差异和反时限特性结合,得出全网统一特性方程的排序函数,由动作时间的大小得到各级保护动作次序,实现自适应故障严重程度的故障识别。
为得到无需逐级整定的反时限特性方程,并尽可能消除故障工况对Ej取值的影响,引入用户自定义的反时限特性方程。仅依据后备保护最小、最大动作时间要求整定反时限特性参数,大大减小了整定计算工作量。
3.2 全网统一方程采用标准反时限特性方程时存在的问题
与传统反时限过流保护特性方程形式一致[14],当测量值采用暂态能量时的全网统一反时限特性方程为:
式中:tj为Rj的反时限动作时间;A、α为反时限特性常数;tp为时间常数;Ep为启动值。
Ej具有距故障点越近、值越大的分布特征,因此所有保护可采用统一的启动值Ep。此时,式(21)中tj为tp的一次函数。由于Ej取值范围非常广,同一保护在不同故障工况下的Ej/Ep值差异也很大,导致tp难以整定。
3.3 用户自定义的反时限特性方程
3.3.1 函数形式
采用箕舌线构造基于能量差异的全网统一特性反时限方程为:
式中:λ为方程参数;zj(Ej)、aj(Ej)表示自变量zj、aj均为Ej的函数。
采用箕舌线构造用户自定义反时限方程的原因见附录D。
正常运行时,Δpj为0;故障时,Δpj不为0。因此,式(22)利用Δpj构造启动判据。取连续3 点的|Δpj|均大于启动值Δpp时,保护启动,即
考虑负荷投切、测量精度的影响,本文取Δpp=0.1 MW。
故障时,满足式(23)的保护启动,并由式(22)计算动作时间。
3.3.2 参数选取原则
为保证zj的值小于等于1,其值由式(24)决定。
由附录D 图D1 知,aj决定了曲线位置,且aj大时tj也大。为实现反时限特性,取aj为:
式中:Emax为有配合关系的两级线路发生最严重故障时的暂态能量最大值。
式(25)中引入对数函数以减小不同故障工况下同一个保护的数据波动、不同故障位置相邻保护的数据差异范围,提升后备保护的整体性能。
当Ej=Emax时,aj=0,tj=0。而各级保护动作时间应大于后备保护最小动作时间tmin,故在Ej=Emax、tj=tmin时,由式(22)可计算出对应的amin,用其修正式(25),以保证动作时间满足后备保护要求。因此,aj的取值为:
各保护动作时间应小于远后备最大动作时间tmax。而λ与tj成正比,λ越大,tj越接近tmax,不利于后备保护间的配合,因此,λ应尽可能小。取极限情况下zj=0,aj=amax=1+amin,结合式(22)得全网统一的λ值为:
给定tmin、tmax后,联立式(26)、式(27)解出全网统一反时限特性方程中的参数amin和λ。
3.4 满足选择性要求的保护动作性能分析
具有配合关系的各保护动作时间需满足选择性要求,即动作时间差值Δt大于保护协调时间间隔(coordination time interval,CTI)[13],有
式中:tj-1为Rj的后备Rj-1动作时间;CTI为CTI 值。
由式(22)计算的tj,其差值主要体现在aj上。不同aj下Δt的变化曲线见附录D 图D2,且Δt最小值出现在z=0 或z=1 处。令aj-1-aj=Δa,则有
由式(29)知,z、Δa、aj都会影响Δt的大小。
当z=0 时,相邻保护恰好满足选择性要求,即Δt=CTI,Δa取得最小值(Δa)min|z=0,其值为:
由式(30)知,(Δa)min|z=0为恒定值。
当z=1 时,Δt为aj、Δa的函数。图6 给出两组tmin、tmax下Δt、aj、Δa的三维关系图。amin、λ由附录D表D1 列出的数据求出,CTI=0.2。
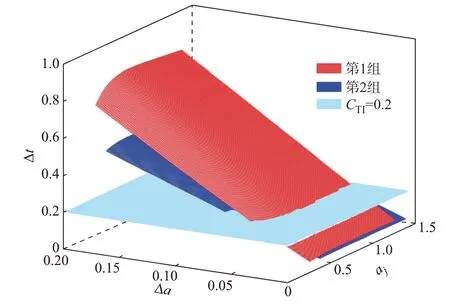
图6 Δt、aj、Δa 的三维关系图Fig.6 Three-dimensional relationship diagram of Δt, aj and Δa
由图6 可知,Δt=0.2 的曲面上方为满足选择性要求的区域。由Δt=0.2 与式(29)中第2 个函数的交线可知,z=1 时Δa的最小值(Δa)min|z=1取在aj=amin处,即有
为保证任意z值下相邻保护满足选择性要求,Δa的最小值(Δa)min应取为:
(Δa)min=max((Δa)min|z=0,(Δa)min|z=1) (32)
因此,由式(26)和式(32)得满足选择性要求时相邻保护暂态能量的关系为:
即Emax、(Δa)min共同决定了满足选择性要求时的保护动作性能,且其值越小、保护性能越好。而网络拓扑固定时Emax是确定的;(Δa)min的取值与CTI 的选取密切相关,CTI 越小,其值越小,越有利于实现相邻保护间的自适应配合。
4 基于稳态电压的动作判别
基于时延的后备保护仅利用暂态信息进行故障识别,而达到式(22)计算的动作时间后备保护是否动作,需由稳态判据再次确认。若故障仍在,则反时限后备保护动作;若故障已消失,则保护返回。因此,构造基于稳态电压的动作判据,当tj时刻Rj的稳态电压幅值Uj低于低电压限值Up时,即动作时间tjdz大于tj、Uj小于Up两个条件同时满足时,反时限后备保护动作。故稳态动作判据为:
依据《DL/T 5729—2016 配电网规划设计技术导则》,不同电压等级下Up的取值不同,表达式为:
式中:UN为额定电压。
图1(b)中f1故障时,R3和R4都正常动作且切除故障后,R5和R6与周围负荷可能形成孤岛继续运行,但其为非计划性孤岛运行[33]。若R5和R6在故障切除后仍满足式(34)的稳态动作判据,说明供电设备已无法正常工作,所提方案仍会跳开R6以减少非计划性孤岛运行的危害。
三相电弧炉(electric arc furnace,EAF)是对电网谐波影响最大的非线性负荷[34]。正常运行时,其产生的谐波干扰可能导致Δpj满足式(23)而计算暂态识别对应的动作时间,但其引起的电压偏差不会超过供电电压偏差的限值,即电弧炉产生的谐波干扰不会达到稳态动作判据。
5 反时限后备保护方案的实现
仅利用网络拓扑中故障分量瞬时实功率的自然差异实现的暂态故障识别、稳态动作判别的接力式后备保护方案流程图见附录D 图D3。
在得到固定网络拓扑下的fmax且给定tmin、tmax后,即可实现基于能量差异的反时限后备保护。该方案具有无需逐级整定、不受调节特性影响、可保护线路全长、各保护自适应配合的优点。
6 仿真验证
6.1 DG 随机接入时的适应性分析
仿真模型和参数见附录E 图E1 和表E1。
tmin、tmax取附录D 表D1 中的第1 组数据。采样率取20 kHz,Up=99 kV。通过改变CB1~CB3、SS的状态来验证所提方案在DG 随机接入时的适应性。
6.1.1 案例1
案例1 对应仅CB1闭合时的网络,其为单端辐射状网络,f2故障时仅考虑R5和R1的配合关系。η表示f2与母线B1的距离占L2的百分比。
最严重故障为R1出口三相金属性短路,可得Emax=20 545 J。
参考2.3 节的理论分析,附录E 图E2 给出n1、η、fmax的三维图,最小适用频带为[0,1 400] Hz,且DG 容量变化时不改变适用频带。
表1 给出n1、η变化时不同负荷LD1下三相金属性短路故障时所提方案的识别结果。仿真中EAF1、EAF2 的参数k1、k2、k3见附录E 表E2[35]。
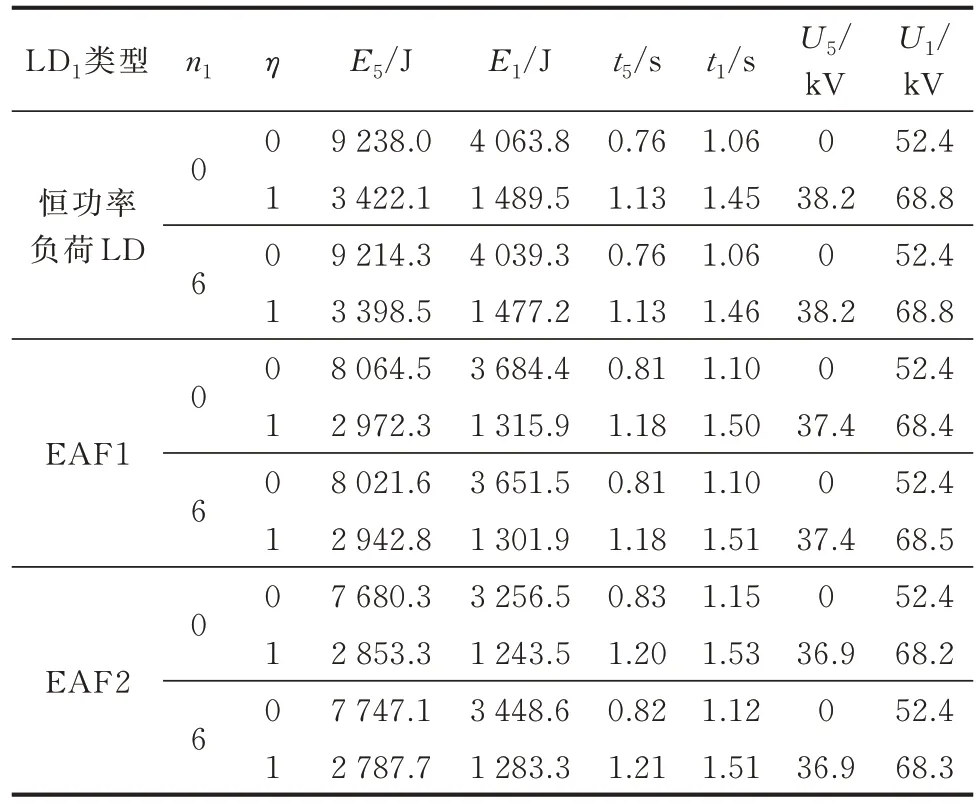
表1 n1、η 变化时不同LD1下的所提方案识别结果Table 1 Identification results of proposed scheme for different LD1 when n1 and η vary
表1 表 明,LD1为 恒 功 率 负 荷LD、EAF1 或EAF2 时,n1、η变化时由式(22)计算的动作时间均满足选择性要求,且故障稳态电压均低于Up值。因此,负荷引起的谐波干扰和DG1容量变化基本均不影响故障识别结果。
图7 给出n1=3、η=0.5,故障起始时刻tf0由0间隔1/8 个工频周期变化时不同故障类型下的后备保护动作时间,Δt15表示R1与R5的动作时间差值。
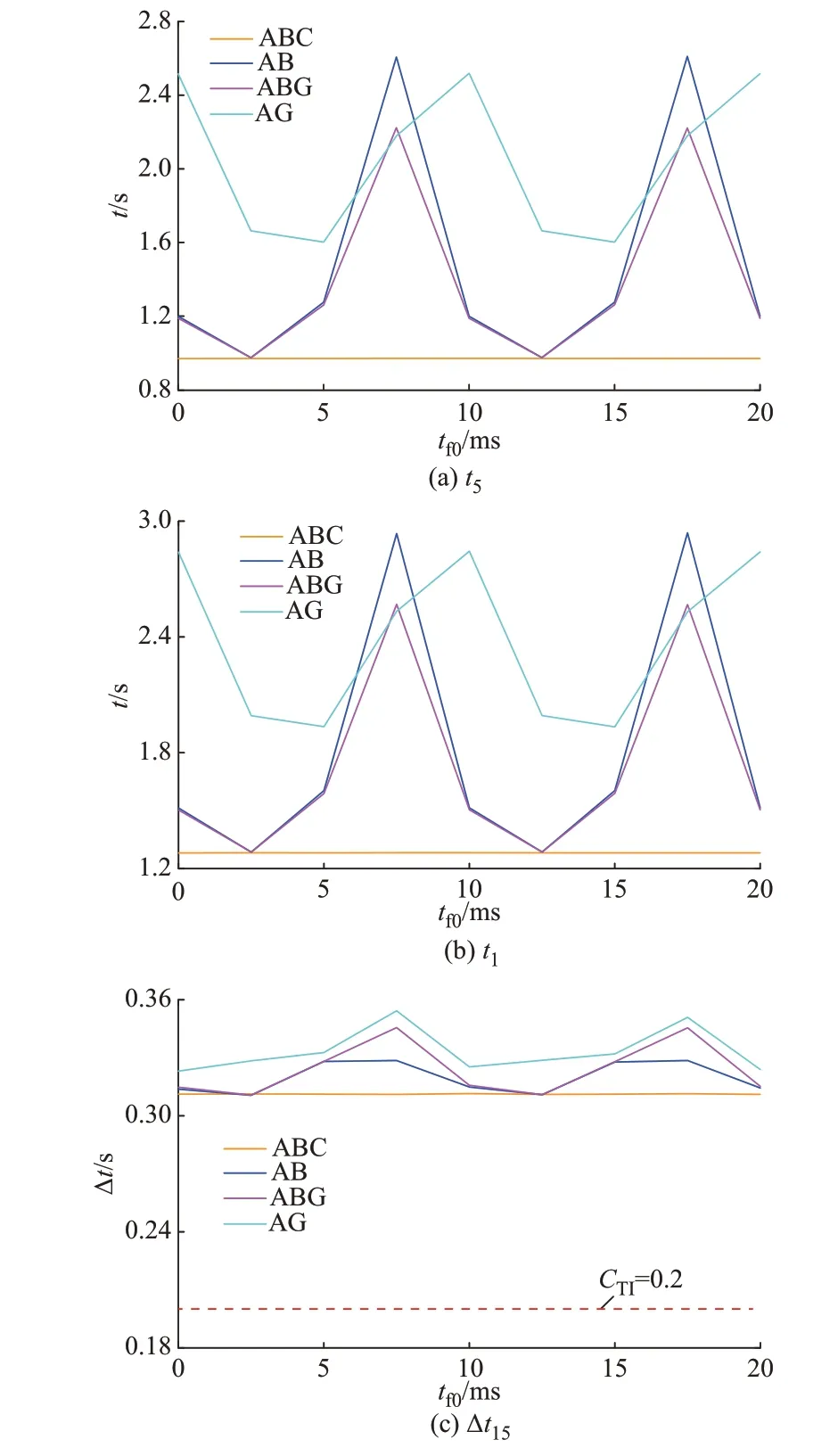
图7 tf0变化时的故障识别结果Fig.7 Fault identification results when tf0 changes
图7(a)、(b)说明故障起始时刻的变化不改变三相短路故障的动作时间,会改变不对称故障时的动作时间,验证了附录C 的正确性。图7(c)说明所提方案在任意故障起始时刻均能实现自适应故障严重程度的故障排序。
表2 给出图7(c)中Δt15最小时三相短路和单相接地故障经过渡电阻Rg故障时的故障识别结果。由表2 可知,经Rg故障时,不同故障类型下的暂态能量取值范围非常广,但采用用户自定义的反时限方程可大大减小暂态能量波动对故障识别的影响,且故障稳态电压均低于Up值。因此,所提方案的耐过渡电阻能力大于300 Ω。
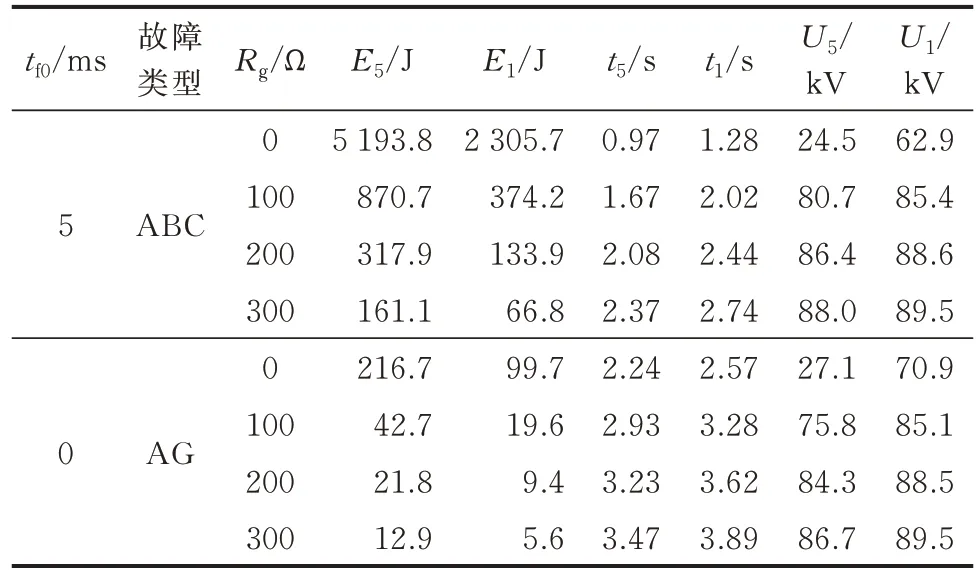
表2 经Rg故障时的故障识别结果Table 2 Fault identification results via Rg fault
案例1 的仿真结果验证了暂态识别方案在DG分散式接入常规电网时适用性。其基本不受控制策略影响,且在不同故障工况下均有自适应性。
6.1.2 案例2
案例2 对应的是CB1和SS 闭合、f4故障或CB2和SS 闭合、f3故障时的转供网络,两种情况下R5和R7的配合关系会发生颠倒。
由2.3 节的理论分析得R5和R7互相配合时的fmax=9 950 Hz。为保证工程应用时滤波环节一致,本节仿真时仍采用[0,1 400] Hz 作为最小适用频带。
表3 给出线路中点发生三相金属性短路故障、开关状态不同时的故障识别结果。
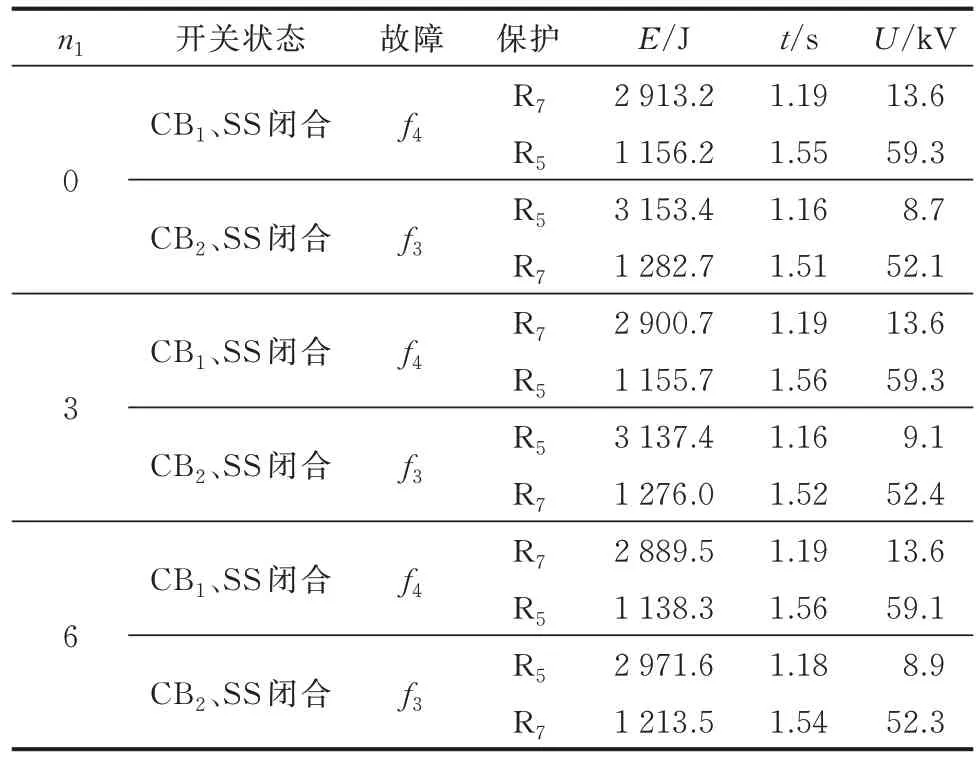
表3 开关状态不同时的故障识别结果Table 3 Fault identification results for different switch states
表3 表明,开关状态变化时,两保护的动作时间是自适应的,且L1小于L3,f3故障时的暂态能量大于f4,动作时间小于f4故障。因此,案例2 的仿真结果验证了所提方案在不更改全网统一特性方程时对系统转供仍具有自适应性。
6.1.3 案例3
案 例3 对 应 的 是CB1和CB3闭 合、CB2和SS 断开时的场景,研究风电场集群化接入后所提方案的适应性。双端供电网络需增加方向判别元件,故本文只考虑感受到正方向故障时的保护配合情况。
风电输出的弱馈性导致Emax的取值与故障位置、分支线接入情况密切相关。本案例中Emax取在R6出口三相金属性短路时,值为3 270 J。
由2.3 节的理论分析得,R6和R10配合时的fmax=2 025 Hz,R5和R1配合时的fmax=1 400 Hz,故取最小适用频带仍为[0,1 400] Hz。
故障发生在f2时风电场侧R6和R10的故障电压u和Δp的时域波形见附录E 图E3,它们的故障电压波形差异非常小,而Δp在故障后3 ms 数据窗内始终具有自然分布特征。
图8 给出f2位于线路中间,n1=3,tf0=0 ms,n2变化时常规电源和风电场侧R6和R10的动作时间差值Δt610与场景、故障类型的关系。
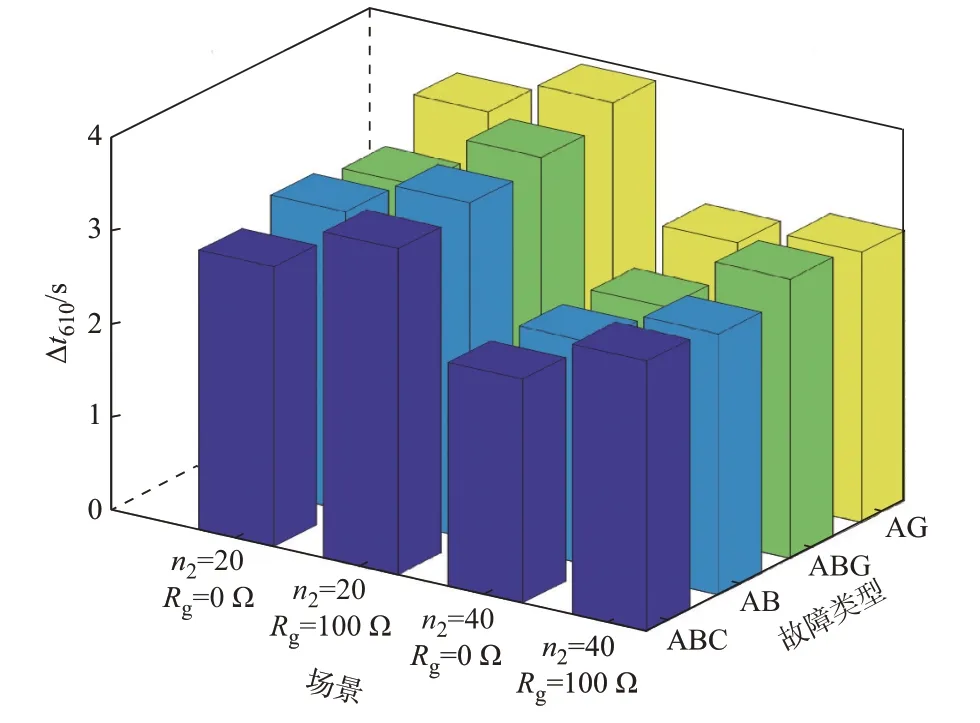
图8 Δt610与场景、故障类型的关系Fig.8 Relationship among Δt610, scenarios and fault types
图8 表明,风电场侧的R6和R10在不同故障工况下均能实现自适应配合。而n2=40、Rg=0 Ω 时的Δt610相比于其他场景时是最小的,说明风电场接入容量最大、金属性故障时的暂态识别结果决定了所提暂态识别方案的适用性,其与线路长度、分支数目、CTI 取值都有关。由图6 可知,式(33)对应的选择性要求在CTI 取值减小时,暂态识别方案性能会提升。
6.2 10 kV 系统的适应性分析
采用图1(a)中母线A 上含有1 条分支线、母线B 上含有DG 和1 条分支线时的电网验证所提方案在10 kV 系统中的适应性。
系统额定容量为SN=5 MV·A,取最大负荷电流ILmax1为 额 定 电 流IN的 1.2 倍 ,可 得It=0.462 kA,L1=10 km,L2=6 km。DG 采 用单个容量为2 MW 的直驱风机,通过改变接入个数n3来改变接入系统的总容量。图1(a)中Emax=20 545 J、适用频带为[0,2 700] Hz,Up=9.3 kV。故障持续时间10 s。
6.2.1 相间故障时的适应性
表4 给出f1位于线路末端、n3变化时流过R2和R1的故障稳态电流I2、I1和所提方案的识别结果。表5 给出L1变化时的故障稳态电流和所提方案的识别结果,最小适用频带取为任意L1下均适用的[0,2 700] Hz。
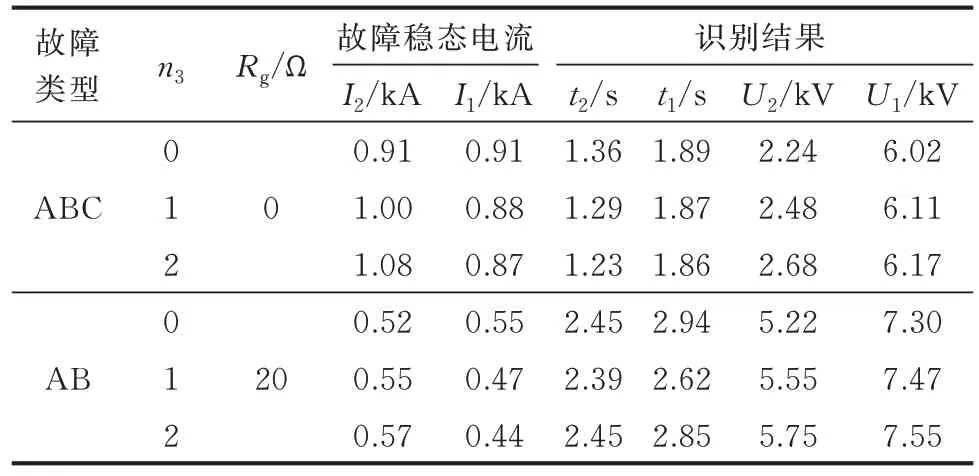
表4 n3变化时的故障稳态电流和所提方案的识别结果Table 4 Fault steady-state current and identification results of proposed scheme when n3 changes
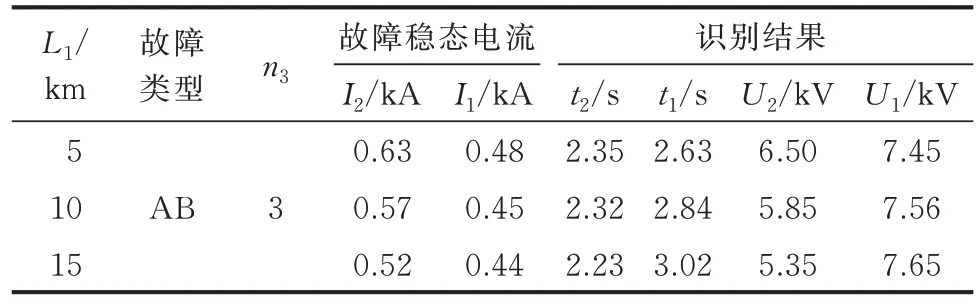
表5 L1变化时的故障稳态电流和所提方案的识别结果Table 5 Fault steady-state current and identification results of proposed scheme when L1 changes
表4 中不同故障类型下,DG 的外汲作用都使得I1随着接入容量的增大而减小。AB 故障下,n3=2时有I1小于IⅢ1,set,R1无法起到远后备的作用。表5 表明,DG 接入容量不变时,I1随着L1的增大而减小,L1=10 km 时 有I1小 于IⅢ1,set。而 表4、表5 中R2和R1的暂态识别结果始终满足选择性要求。因此,DG接入容量或L1增大时,已有阶段式配合的后备保护可能失配,而所提方案可适应它们的变化并实现自适应配合。
6.2.2 单相接地故障时的适应性
表6 给出不同接地方式下f1位于线路首端、n3变化时发生AG 故障的故障识别结果。由表6 可知,小电阻接地方式下R2、R1的暂态能量和稳态电压都是有差异的,但随着DG 容量增大,差异减小,这是DG 对故障前电压的支撑作用导致的。而小电流接地方式下它们的暂态能量和差异都非常小,稳态电压差异也非常小。0 模等效电路中,小电阻、小电流接地方式的中性点等效阻抗分别为中性点接入电阻、无穷大[36]。而当0 模阻抗远大于1、2 模阻抗时,相邻保护间1 模或2 模的电压差异会非常小,暂态能量的差异也会非常小。因此,所提方案可适用于小电阻接地方式而不适用于小电流接地方式。
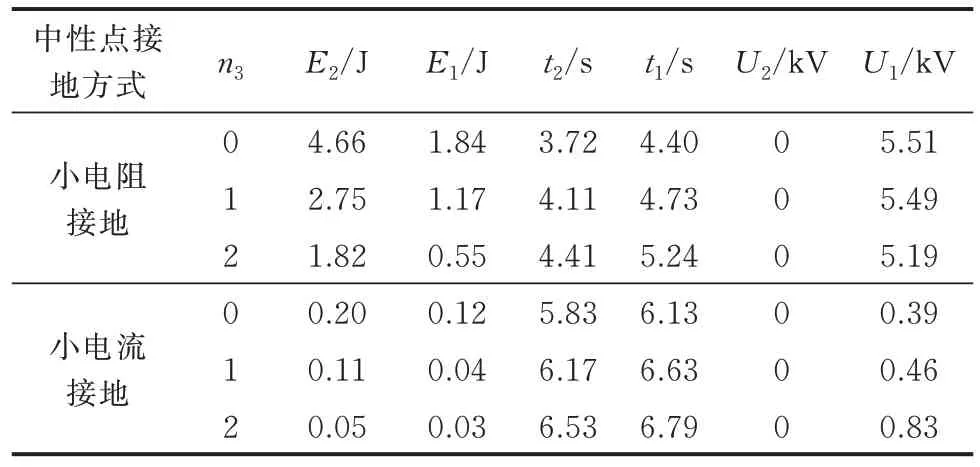
表6 不同接地方式下AG 故障的故障识别结果Table 6 Fault identification results of AG faults with different grounding modes
7 结语
本文分析了新型电力系统的故障分量瞬时实功率的暂态特征分布,提出了暂态故障识别、稳态动作判别的接力式反时限后备保护方案,得出如下结论:
1)适用频带内,故障分量瞬时实功率具有距故障点越近、值越大的自然分布特征,仅利用此频段的暂态能量自然差异即可实现自适应故障严重程度的故障识别,无需通信且对采样率要求不高;
2)全网采用统一反时限特性方程,无需逐级整定,且具有自适应网络拓扑变化的能力;
3)利用故障全过程电气量的后备保护方案,可自适应DG 分散化或集群化接入的场景,具有很强的耐过渡电阻能力;
4)针对所提方案不适用于小电流接地方式下的单相接地故障,后期将专门研究适用于该场景的自适应配合方案。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
