基于潮流追踪模块度的虚拟微电网分区规划

蒋 玮，撒鹏程，贾 俊，杨 旎，解 兵，邓一帆

（1.东南大学电气工程学院，江苏省南京市 210096；2.国网江苏省电力有限公司泰州供电公司，江苏省泰州市 225300）

0 引言

近年来，清洁能源、低碳经济的需求日益增长，可再生能源的利用和电力系统的智能化越来越被关注［1-3］。在能源结构转变的背景下，微电网技术被人们提出并主要应用于含清洁能源的一体化资源互补的相关研究中。作为促进分布式电源（distributed generator，DG）接入配电网的友好技术手段，微电网常配置光伏与储能以参与配电网调峰优化调度，进行微电网能量管理，将光储微电网作为整体接入电网进行容量配置等［4-9］。

在现代电网的发展过程中，传统配电网（conventional distribution network，CDN）的基础设施与庞大规模在一定程度上限制了其向智能化的进一步发展。但是，由于微电网不大的规模和有限的能量处理能力，在现实电网中仿照微电网的运行模式将大规模的配电网进行改造并不容易。因此，虚拟微电网（virtual microgrid，VM）逐渐引起了关注，作为一种向着智能化方向升级CDN 的新方法，VM在划分CDN 的基础上实现了区域间的互联。文献［10］对VM 以及其开发的通用框架进行了明确的定义，VM 是基于CDN 结构的虚拟孤岛系统，具有与微电网相似的控制策略和运行模式且能够适应未来电网的智能化需求。VM 与微电网相似的特性主要包括DG 的高渗透性、运行模式多样、自适应性与自恢复力强等。除此之外，VM 与微电网最大的不同之处在于其内部的孤岛是“虚拟”的，即其具有虚拟动态的边界而并非传统微电网固定的孤岛关系。

可控DG（controllable DG，CDG）是一种能够根据负载需求来自主控制发电功率和电压的DG 系统，通常由多个小型发电机或储能系统组成，并且可以通过VM 中的互联网进行远程监控和控制，进而可以实时调整其输出功率及电压。

对内部各种资源的合理配置、调度与能量管理是建立在对VM 边界合理划分的基础上的，作为VM 概念的基础与关键，如何合理且有效地分区必然是研究的重点。近些年来，学者们对于VM 各区域的划分方式进行了深入的研究，目前对于VM 分区的划分方法大致可以分为以下两类：

1）基于负荷聚类进行划分。文献［11］将分区的聚类算法分为谱聚类、分层聚类和k-means 聚类3 种，并详细比较了3 类方法各自的特点与适用情况；文献［12］提出一种新的VM 各分区形成问题的启发式求解方法，使用k-means 聚类方法，以DG 节点为区域中心形成微网格；文献［13］考虑到分区结果对子系统恢复的影响，基于谱聚类的分区结果，提出了基于粗糙集的分区调整策略。

2）以最基本的电力网络拓扑进行划分。文献［14］建立了以电气距离为权重的网络模型，将改进粒子群优化算法应用于电网无功分区；文献［15-18］与无功电压分区控制有关，均为在电网的合理分区基础上评估区域无功平衡能力，进行光伏集群控制等。

3）与图论相关的划分。文献［19］提出基于图割理论的备用动态分区方法，建立了考虑分区备用的优化调度模型。

现有研究在以上方面对VM 分区的相关研究作出了巨大贡献，但仍然存在以下问题：分区的依据仍以配电网的自身拓扑结构为主，算法以聚类为主，对于各孤岛内的能源供给与需求之间的协调问题很难兼顾考虑；分区过程相对独立，一般进行于各类资源配置较为确定的情况下；对划分后VM 的安全裕度考虑不足。

针对VM 分区过程中存在的以上问题，本文提出了一种双层分区规划框架，全文主要工作如下：

1）建立了基于潮流追踪的模块度指标作为分区主要目标，该指标将潮流追踪得到的源荷分配系数作为变量代替原始模块度定义中的边权，在兼顾评估区域内能源利用率水平的同时让VM 整体区域内外源荷连接强弱的整体性最高，即区内连接强、区间连接弱。

2）提出了CDG 配置与分区同时进行的上层分区规划模型，模型中在分区的同时对各区域CDG 进行位置与出力的配置，边界确定的同时将CDG 规划完毕，同时保证了边界与CDG 配置的合理性。

3）提出了协调可削减负荷与CDG 的下层故障应对模型，对分区规划完成的VM 进行故障下的分析，协调故障情况下的可削减负荷控制与CDG 增发量。下层模型中在定义了故障区域、缓冲区域的基础上，提出了负荷削减补偿代价与CDG 增发成本的目标函数，最终形成确定分区方案下每种故障的最佳应对策略。

1 综合CDG 配置和故障应对策略的VM 双层分区规划框架

为了解决上文提到的VM 分区问题，本文首先提出了综合CDG 配置和故障应对策略的VM 双层分区规划框架［20-23］。

在本框架中，首先考虑的是原始区域电网中存在着的一些诸如风电、光伏等DG，由于其固有的波动性，这类资源一般被称为不可控 DG（uncontrollable DG，NDG），与 功 率 电 压 可 控 的CDG 相对，其人为控制较困难，一般的处理方法是对其不确定性进行建模处理。这里将每台CDG 作为各自划分出的孤岛管理中心，即划分的总孤岛数等于CDG 数量。

上层分区规划模型中，若干NDG 的位置和出力以及电网拓扑属于固定的常量，以基于潮流追踪模块度最大和孤岛内部电压质量分布最优为目标；决策变量为各孤岛管理中心——CDG 的位置和出力，由各NDG 位置以及电网拓扑求解出管理各区域运行的CDG 信息；约束条件包括机组运行约束、孤岛划分约束、孤岛间电压约束、孤岛潮流平衡约束和孤岛运行安全约束。

上层模型求解出的CDG 位置和出力将作为上下层传递的参数传入下层故障应对模型中，对于发生故障的区域，进行区域内的负荷削减以及缓冲区域内的CDG 增发以缓解故障区域的失电状况。在下层模型中，以负荷削减补偿代价最低和CDG 出力增加成本最低为目标；决策变量为配合调节的故障区域负荷削减量与缓冲区域CDG 增发量；约束条件除了上层模型中的孤岛间电压约束、孤岛潮流平衡约束和孤岛运行安全约束外，还包括负荷削减约束。

图1 所示为VM 的分区规划与故障应对示意图。第1 阶段为分区配置，正常运行情况下在对系统进行分区的同时对CDG 进行配置，确保每个孤岛内有且仅有一台CDG。第2 阶段为故障发生，实际电网中故障类型较多，本文中简化为某区域CDG 发生故障而无法正常出力，该区域为故障区域。第3 阶段为故障应对，选取与故障区域相邻的某区域作为缓冲区域，在对故障区域的可削减负荷进行削减的同时，提高缓冲区域CDG 的出力以保证两个区域中线路、负荷的安全运行。值得注意的是，VM 的孤岛运行为常态，而非孤岛运行仅为故障发生时的暂时状态。

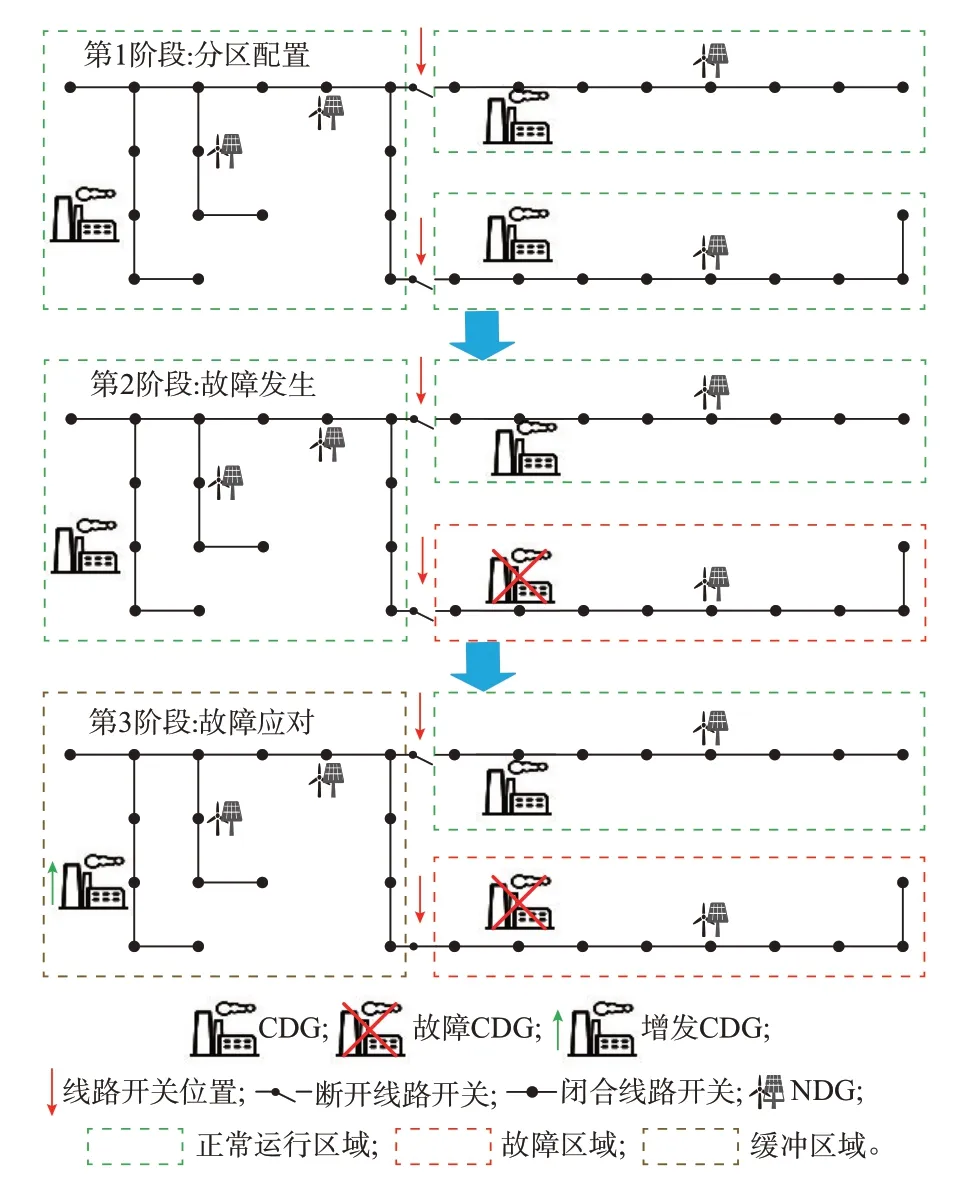
图1 分区规划与故障应对示意图Fig.1 Schematic diagram of partitioning planning and fault response

2 基于潮流追踪的模块度指标

2.1 潮流追踪解析算法

潮流追踪作为一种计算源荷之间功率传输的算法工具，在明确网络中所有潮流分布的基础上，其可以建立起所有发电机出力对负荷分配的模型。主要计算公式如下［24］：

式 中：A为 顺 流 分 配 矩 阵［24］；PGG=diag(P，P，…，P) 和PTT=diag(P1t，P2t，…，Pnt) 分 别 为n×n节点电源有功出力与节点总注入有功功率对角矩阵，其中，系统总节点数n=|N|，N为系统中所有节点的集合；P为节点i处所有DG 的有功功率注入；Pit为节点i处所有的有功功率注入；T为计算得到的分配系数矩阵；Tij表示节点i处电源出力辐射到所有节点中节点j所包含的比例；PDj为节点j的有功负荷的大小；Pi→j表示节点i上电源对负荷节点j的功率分配，将所有的Pi→j综合为潮流追踪矩阵PTR，其元素为PTR，ij。

在矩阵T中，由于每个节点的负荷一定100%来源于系统中的所有电源，各列元素之和等于1。值得注意的是，矩阵中各行元素之和不一定为1，原图如下：假设系统中存在一个含电源且不含任何流入功率的节点g，显然节点g的负荷只汲取于节点g的电源，即Tij=1，而该电源必然还辐射至其他节点，所以该行元素之和必然大于1。在严谨计算中，需将线路损耗等效为线路两端的等值负荷，本文为了简化处理，仅在进行潮流追踪时忽略了线路损耗而直接将网络视为无损网络。

任何明确潮流分布的系统经过式（1）—式（3）的计算都可以得到潮流追踪矩阵PTR。虽然一个潮流断面仅对应一个确定的PTR，ij，但是在系统电源和负荷波动不大的情况下，分配系数矩阵T中的值差异是不大的，所以矩阵T也可以间接反映出该系统内各电源与各负荷间的利用情况。以T中第i行数值为例，其表示节点i所有电源传输至各节点负荷的含量百分比，所以T中第i行的平均数值越大（只计算辐射到的负荷节点），代表节点i处的电源在所有可辐射到的负荷节点的利用率越高。

2.2 基于潮流追踪的模块度指标的建立

二分网络定义为由两部分不同类型节点构成的网络，现实中诸如疾病-基因网络、投资者-股份公司网络等都属于二分网络［25］。在电力系统的研究中同理也可以将源荷网络视为标准的二分网络。一般意义上，对于网络进行划分本质上属于社区划分问题，绝大多数目标都是希望各社区内部节点联系相对紧密，各社区间联系相对稀疏。对于源荷二分网络的划分也不例外，本文的划分目的是希望区域内节点的源荷连接强度高而区域间节点的源荷连接强度低。所以，本节将模块度M的概念与潮流追踪进行结合，可以用该指标衡量某种分区方案区域内外源荷连接强弱的整体性，即区内源荷连接强、区间源荷连接弱［26-27］。

式中：eij为连接节点i和节点j边的权重（简称边权）；m为网络所有边权之和；ki表示所有与节点i相连的边 权 之 和；δij为0-1 变 量，取1 表 示 节 点i和 节 点j在同一微电网内，否则为0；kikj/(2m)项表示节点间随机连接所产生的边数的期望值，具体推导过程可参考文献［28］。

式（4）—式（6）为模块度定义式，模块度最早由Newman 在文献［28-29］中提出，式（4）等号右侧为模块度的原始定义。作为一种社团发现算法，在Newman 的原始定义中，模块度指标用于衡量节点之间连接的紧密程度，所以边权eij的原始定义为：

此时由eij组成的边权矩阵E为对称的稀疏阵。

在加权网络中，边权eij也可以由其他体现节点间权重的量代替，典型地可选取节点间电气距离代替，该值保证了边权矩阵的对称性。当节点i和节点j在同一微电网内时δij=1，否则δij=0。M为改进的基于潮流追踪的二分模块度指标，目的是用上文提到的Tij代替eij，即

由此可知直接进行替换是可行的，如式（8）所示，替换过程中的合理性以及与原始定义的差异性说明如下：

1）Tij的定义并非只存在于相连的节点间，而是只要节点i与节点j在同一孤岛内，且其中一个节点含电源注入时，Tij就可能有取值。传统的节点连接强度仅定义在物理上相连的两个节点间，一般与节点间的线路参数、潮流参数有关，而这里可以用Tij来评估任意两个节点间的源荷连接强度，当然前提是这两个节点必须分别是电源节点与负荷节点。

2）原始定义中eij与eji完全等效，而绝大多数情况下Tij≠Tji。在原始定义的计算循环中，由于eijkikj/(2m)=eji-kjki/(2m)，故循环中这两项完全一致，而改进后的M指标中的这两项不相等。

3）根据潮流追踪的定义，显然有

将边权按照式（9）处理后，即与加权网络下的模块度定义完全等效。此时，便可用M来刻画某种分区方案区域内外连接强弱的整体性。在同一多节点系统的不同划分方式下，孤岛内部的源荷间功率传输关联越紧密，对应的eij-kikj/(2m)项也越大。当仅考虑划分方式时，在进行每次划分的时候计算M的值，M取值越大，表示区域内节点的源荷连接强度越高而区域间节点的源荷连接强度越低。此时，该加权网络的划分方式应为最为合理且理想的划分。但是，目标M随着分区数的增加不会无限制增加，一般M的极值会出现在0.3～0.7。

3 双层分区规划模型

在本文的双层模型中，上下层的参数传递是单向的，上层模型对若干种不同开关位置的分区方案进行CDG 的配置规划，将CDG 位置及出力传入下层后，在下层模型中对每种分区方案分别进行故障应对策略的分析，对各方案进行筛选，最终综合上下层模型遴选出最佳的分区方案与对应的最佳CDG配置与故障应对策略。

3.1 上层分区规划模型

如图1 框架所示，上层模型以不同开关位置与CDG 配置情况为研究对象，目标函数为潮流追踪模块度最大和孤岛内部电压质量分布最优，求解出各孤岛中CDG 的位置和有功无功出力。

3.1.1 上层模型目标函数

1）简化的潮流追踪模块度

在2.2 节的指标定义中，若将式（4）—式（6）和式（8）直接作为目标函数，目标函数涉及变量的数目是巨大的，求解起来非常困难，所以有必要对eijkikj/(2m)项进行进一步的简化。由于各孤岛中的电源包括一台待配置的CDG 与若干NDG，在所测试的正常运行状态下，CDG 作为孤岛的能量管理中心，其出力远大于NDG 的出力，故在所有以节点i为起始节点的eij-kikj/(2m)项中，仅保留以CDG节点为起始节点的项，如式（10）所示。

式中：NCDG为所有CDG 节点的集合。为了降低区域间源荷连接强度、提高区域内的源荷连接强度，应使F1最大化。

2）孤岛内部电压质量分布

在断开开关的孤岛内部，供电主体只有单独的CDG 以及确定的若干NDG，需要评估孤岛内部各节点的电压幅值波动情况，如式（11）所示。

式中：S为所有孤岛的集合，| |S为孤岛数；vis为节点分区二进制变量，即节点i属于孤岛s时为1，反之为0，具体定义在3.1.2 节中；V为系统参考电压幅值的平方；V为节点i电压幅值的平方；Ns为孤岛s中所有节点的集合，| |Ns为孤岛s内包含的节点数。显然应有：

除CDG 节点外，孤岛内部的所有节点电压幅值在系统参考电压幅值上下波动，为了使节点电压波动更小，应使F2最小化。

上层优化模型的总目标函数为：

式 中：α1和α2分 别 为F1和F2的 权 重 系 数，可 根 据 实际问题需要选取。由于F1和F2在式中均已归一至［0，1］内，故总目标函数可将二者加权相加。

3.1.2 上层模型约束条件

1）机组运行约束

为CDG 的CDG 定 义CDG 配 置 变 量zki，当 第k台CDG 位于节点i时zki=1，反之zki=0；在此基础上应有：

式中：K为所有CDG 的集合。

式（15）分别保证了一台CDG 只能同时连接一个节点、一个节点最多只能同时连接一台CDG。CDG 的有功、无功出力应满足以下约束：

对于节点i来说，除了CDG 外该节点也可能连接着若干NDG，与P相同，定义为节点i处所有DG 的无功注入，二者应满足：

2）孤岛划分约束

首先，定义节点分区变量vis，在此基础上应保证划分结果中区域间无重叠部分，即每个节点必须属于且仅属于一个孤岛区域：

同时，在本文中应保证一个孤岛内有且仅有一台CDG：

将节点划分完毕后，应判断各线路（i，j）是否属于孤岛s，显然这取决于该线路两端节点i和j是否属于该孤岛。定义线路分区变量cs，ij，当线路（i，j）属于孤岛s时cs，ij=1，反之cs，ij=0，应有：

式中：Ωl为系统中所有线路的集合。

为了尽量避免非线性的约束条件，含二进制变量乘积形式的约束式（22）可以等效转换为：

系统在正常孤岛状态下运行时孤岛间的线路应处于断开状态。定义线路开关状态变量xij，当线路（i，j）仍恢复运行时xij=1，线路（i，j）断开时xij=0，应有：

即某条线路的线路开关状态变量为该线路的所有线路分区变量之和。划分后的系统仍应保持原先的辐射状运行情况，由下式保证：

即所有线路的线路开关状态变量之和恒等于总节点数减去孤岛数。由于一个孤岛内有且仅有一台CDG，所以孤岛数应与CDG 数量|K|相等，即

3）孤岛间电压约束

对于线路开关设置的位置，当某侧的孤岛内出现故障时，往往需要闭合该线路开关以使用另一侧孤岛内的电源为该故障区域供电。为了尽量减少开关闭合时的功率冲击，应使断开开关两端节点电压的幅值尽量接近。以下约束表示断开线路两端电压平方差相较于参考电压幅值平方最大不超过1%：

其中1-xij项保证了该约束只存在于断开线路两端电压之间。

4）潮流平衡约束

配电网潮流方程分为两类：节点注入方程和支路潮流方程。由于方程中非凸非线性项的大量存在，故需要将该模型转化为包含整数变量的二阶锥规划模型［30］：

其中，式（28）为节点注入功率平衡方程，式（29）为线路电压降落方程；Pij和Qij分别为线路（i，j）的有功、无功潮流；I为线路（i，j）电流幅值的平方；与相同，定义为节点i的无功负荷的大小；Rij、Xij和Zij分别为线路（i，j）的电阻、电抗和阻抗值；bij为松弛变量，其取值取决于线路（i，j）的开关状态：xij=0 时，线路（i，j）断开，电压降落方程式（29）不必满 足，bij的 取 值 范 围 根 据 式（30）为[-Vsqr0，Vsqr0]；xij=1 时，线路（i，j）闭合，bij=0，式（29）严格满足。

5）安全运行约束

在明确线路开断状态的基础上，孤岛内部各节点电压与各线路潮流均在一定范围内：

式（31）保证了CDG 即孤岛内主电源节点电压为V0，且所有节点电压都在可接受的电压波动范围内；ε为电压波动范围参数，这里取0.05。

3.2 下层故障应对模型

在VM 发生一系列未知故障时，需要将控制整个VM 孤岛运行的线路开关进行适当的闭合操作。定义Ωfa为系统中的基本故障场景集，各基本故障场景对应的概率为δ1，δ2，…，δfa（fa为场景数）。在VM运行过程中，发电机组出力故障为常见故障之一，这里以VM 中某台CDG 出力故障为基本故障场景，由于VM 中CDG 共| |K台，且简单处理为各台CDG 故障概率相等，故应有

当故障区域只连接一处线路开关时，毫无疑问应闭合该处开关并以连接的区域为缓冲区域。而当故障区域与多个区域毗邻，同时连接多个线路开关时，为了尽量减少该故障对其他区域正常运行的影响，一般只闭合一处线路开关。这里统一规定：为了给缓冲区域CDG 出力的提高留下尽可能多的裕度，将所有相邻区域中CDG 出力最少的区域作为缓冲区域，对应的连接线路开关为应闭合的开关。由式（25）可知，辐射状线路中两个相邻区域间有且仅有一条线路开关，不需要考虑确定缓冲区域后闭合哪条线路开关的问题。

3.2.1 下层模型目标函数

1）负荷削减补偿代价

电网对于产生电源故障的孤岛区域可通过对削减负荷实施一定补偿的形式来鼓励该处用户调整其高功率用电设施，进而可对该处的负荷起到一定的削峰效果。目标函数为故障区域总负荷削减所需要的补偿代价，即故障集中所有故障情况下负荷削减补偿代价之和：

式中：Al为基本故障场景集Ωfa中第l种场景；PLoad，cut，l为第l种场景下故障区域所削减的有功出力的总和；KL为补偿削减电力的代价系数；Nfa为故障区域的 节 点 集 合；Pcut，h，l为 第l种 场 景 下 节 点h削 减 的 有功出力。考虑到故障处理的经济性，f1应最小化。

2）CDG 出力增加成本

提高缓冲区域CDG 出力也需要一定的成本。目标函数为缓冲区域CDG 增发的有功出力对应的成本，即故障集中所有故障情况下CDG 增加成本之和。

式中：ΔPCDG，ad，l为第l种场景下缓冲区域CDG 相较于故障前正常有功出力的增发值；KCDG为每台CDG的有功出力成本系数。同样考虑到故障处理的经济性，f2应最小化。

下层优化模型希望对故障处理的成本最小，故总目标函数为：

3.2.2 下层模型约束条件

对于下层模型来说，CDG 配置变量zki、线路开关状态变量xij均为已知。

1）机组运行约束与故障无关的区域中，CDG 出力为常量，故障区域中CDG 被移除，缓冲区域CDG仍应满足式（16）—式（18），各节点、仍应满足式（19）。

2）孤岛划分约束。每种故障下应根据故障情况闭合对应的线路开关：

式中：xij，l为第l种场景下闭合的开关。

3）孤岛间电压约束仍应满足式（27）。

4）削减负荷容量约束。故障区域每个节点削减的有功负荷功率应有一定的上限：

式中：μh为节点h的最大负荷削减系数，一般可根据需要在0.3～0.7 取值。节点无功负荷随有功负荷变化，取第l种场景下节点h削减的无功负荷QLoad，cut，l=PLoad，cut，l/3。

5）潮流平衡约束。由于削减负荷的存在，节点注入功率平衡方程式（28）需稍作改动为：

式 中：Pcut，i和Qcut，i分 别 为 节 点i负 荷 削 减 的 有 功 和无功部分，其都满足式（40）约束。为了与式（28）形式上保持一致，式（41）在这里省略了每种变量的下标l，其对基本故障场景集Ωfa中每个场景Al都满足。

类似的，每个场景Al还应满足式（29）和式（30）。

6）安全运行约束仍应满足式（31）和式（32）。

4 算例分析

在IEEE 33 节点模型上对本文提出的VM 分区规划方法进行验证。模型被设置于10 kV 的电压等级下，所有节点均设置了确定的负荷，其取值统一为（0.15+j0.05）MW。NDGNDG1 和NDG2 出力参数见附录A 表A1。

算例分析大致框架简述如下：1）对已有分区方案进行上层优化并筛选方案；2）对筛选出的方案进行下层优化并进一步筛选；3）列出最终筛选出的若干方案优化过程中的规划结果并进行对比。

4.1 不同分区方案的上层分区规划

本算例中将CDG 数量设置为4，即将整个系统划分为4 个孤岛。设置不同分区方案的方式如下：考虑到实际电网中线路切除位置一般相对固定，在IEEE 33 节点模型中将3 处开关设置于固定位置，考虑到分割区域的均匀性，每个开关可选择性地置于两条相邻线路之一的位置上，共形成8 种分区方案，如附录A 表A2 所示。

8 种分区方案分别在上层模型中进行优化配置，取α1=α2=0.5，上层模型中各方案的最优解对应的目标函数值F、F1和F2见表1。

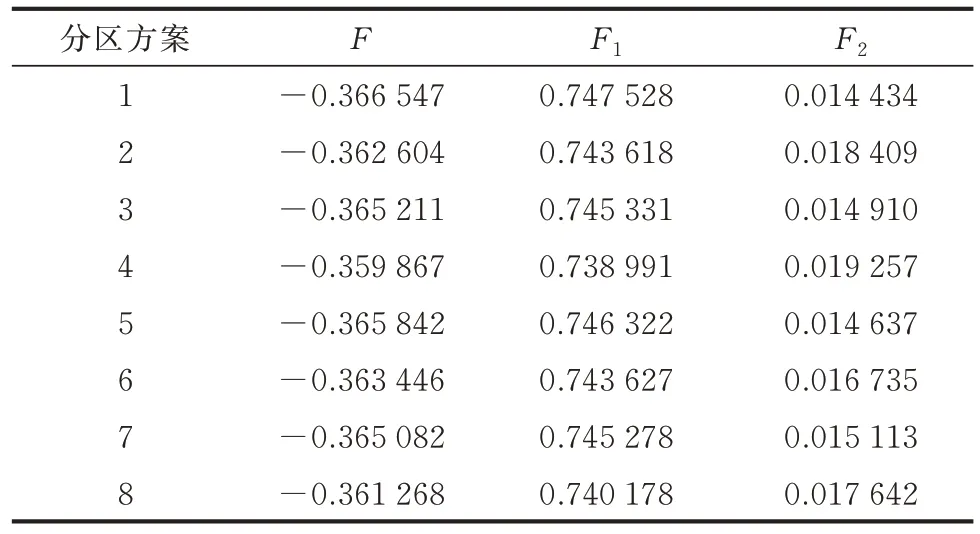
表1 上层模型中各分区方案最优解对应的目标函数值Table 1 Objective function values corresponding to optimal solution of each partitioning scheme in upper-level model

8 种方案的F1值均在0.74 左右，其中只有方案4和8 的F1值相对较低，可以认为其余6 种方案区域内源荷连接强度更高且区域间源荷连接强度更低。同时，这个数值也符合模块度理论定义的最佳数值范围，可以认为在每种方案下的CDG 配置可以使考虑潮流追踪的模块度指标最优。对于与孤岛内部电压质量分布相关的F2值，方案2、4、8 明显高于其他方案，其各孤岛内电压波动幅度较大。

对于VM，保证微电网全局最优的同时，由于在日常运行情况下往往是分区运行，故也需要保证各分区的M不应相差过大。方案1～8 的4 个分区的模块度（M1、M2、M3、M4）及标准差对比如图2 所示。

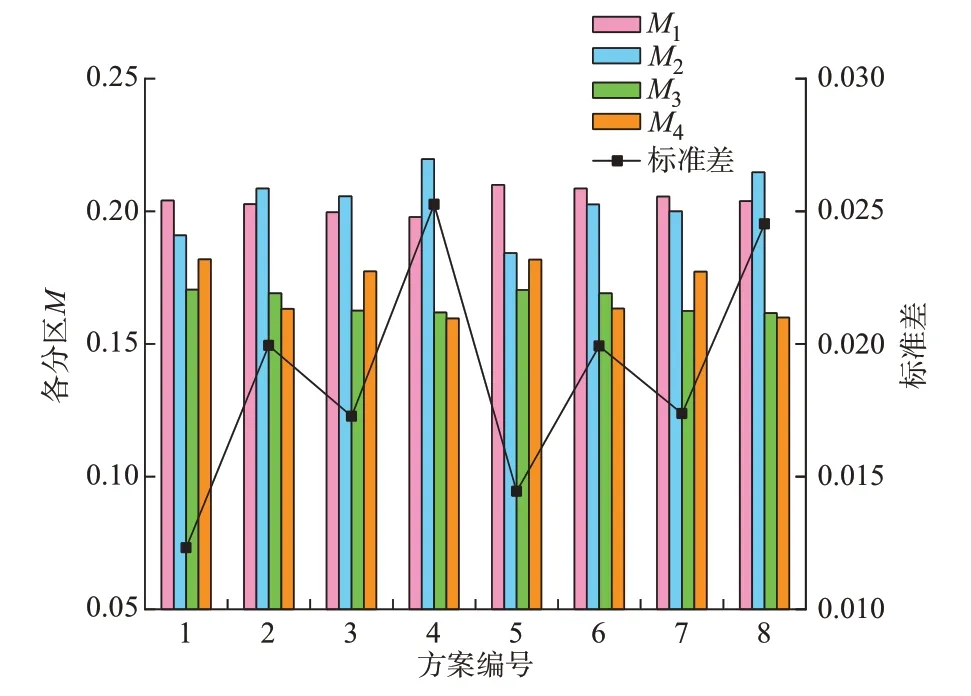
图2 各方案各分区M 与总标准差Fig.2 M and total standard deviations of each partition in each scheme

显然方案1、3、5、7 的各分区M标准差相对更小，其各分区M较为接近，而其他方案各分区M差异较大，在分区运行的极端情况下可能会形成某个区域的能源消纳率较低的情形。算例在上层模型的分区方案中筛选出了4 种分区方案（方案1、3、5、7）并分别配置了各分区的CDG，这4 种方案将在下层模型中进行进一步筛选和故障处理策略的优化。为方便起见，将这4 种筛选出的方案命名为方案集1。

4.2 不同分区方案的下层故障应对

在分析故障应对情景时，仍应说明的是：故障状态为VM 的暂时状态，并不能代表正常的孤岛运行状态。首先，方案集1 中各方案所配置的CDG 节点见附录A 表A3，在下层模型中CDG 节点固定，除故障区域和缓冲区域外的区域CDG 出力也是不变的。

在实际电网中，考虑到各类用户负荷的意愿，并非每个节点的负荷均为可削减负荷，故在每个分区内各取3 个节点为可削减负荷节点，为方便起见，不同方案间划分不同的3 个节点3、26、10 不选为可削减负荷节点。考虑到这类节点应均匀分布，可削减节点取为：18、21、22，4、7、25，12、14、16，28、30、32。最大负荷削减系数μh统一取0.6，补偿削减电力的代价系数KL和每台CDG 有功出力成本系数KCDG各取为3 600 元/MW 和5 400 元/MW。下层模型中方案集1 各方案的最优解对应的目标函数值f、f1和f2，见附录A 表A4。

显然，方案5 和7 的开关闭合情况下的处理策略成本相对较低，二者的划分方案在正常运行以及故障运行情况下的安全性、各分区综合能源消纳率以及故障处理成本最优。将这两种筛选出的方案命名为方案集2。

4.3 优选出的分区方案规划结果

图3 所示为方案集2 中分区方案的分区与配置结果示意图。图中：P和Q分别表示有功、无功功率。正常运行状态下CDG 的出力、有功潮流方向也标注于图中。

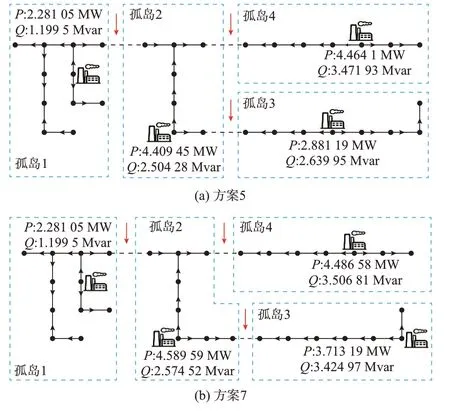
图3 方案集2 各方案分区与配置结果Fig.3 Partitioning and configuration results for each scheme in scheme set 2

两种最终优选出的方案在分区与配置结果上的差异在于孤岛2 和3 间的线路开关位置上，这也导致了方案7 相对于方案5 孤岛3 内CDG 配置位置偏向于线路末端的变化。

在上层模型中的潮流追踪模块度相关的目标函数F1中计算了正常运行状态下各分区内CDG 的潮流追踪情况，图4 给出了方案集2 各方案4 分区正常运行状态下CDG 潮流追踪情况，即矩阵T中CDG所在行的所有值。图中：绿色线路代表该区域CDG的辐射情况，节点处的百分数为该节点负荷来源于CDG 有功出力的含量。

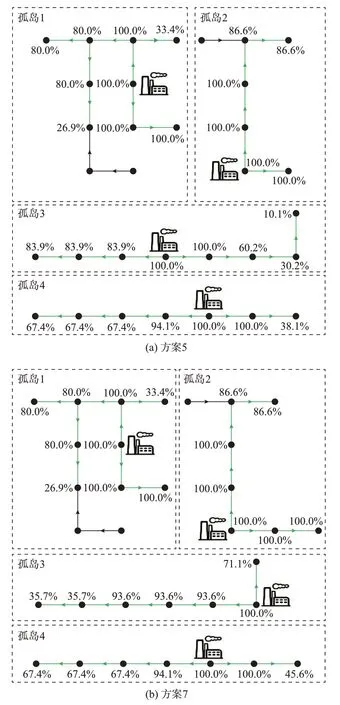
图4 方案集2 各方案4 分区正常运行状态下CDG 潮流追踪情况Fig.4 CDG power flow tracking status under normal operation of four partitions for each scheme in scheme set 2

由2.1 节中的电源利用率与T中值的对应关系可知：对于孤岛1，二者含量一致；对于孤岛2，方案5与方案7 的各节点平均含量分别为95.5% 和96.2%；对于孤岛3，方案5 与方案7 的各节点平均含量分别为69.0%和74.8%；对于孤岛4，方案5 与方案7 的各节点平均含量分别为76.3%和77.4%。显然，孤岛1、2、4 均值差异不大，而孤岛3 明显比方案7 的CDG 利 用 率 更 高。

下层模型中的最优解为各方案的故障应对策略，方案集2 各方案4 种CDG 故障下各自应对策略如表2 所示。表中：负荷削减量为故障区域内的，CDG 有功增发量为缓冲区域内的。

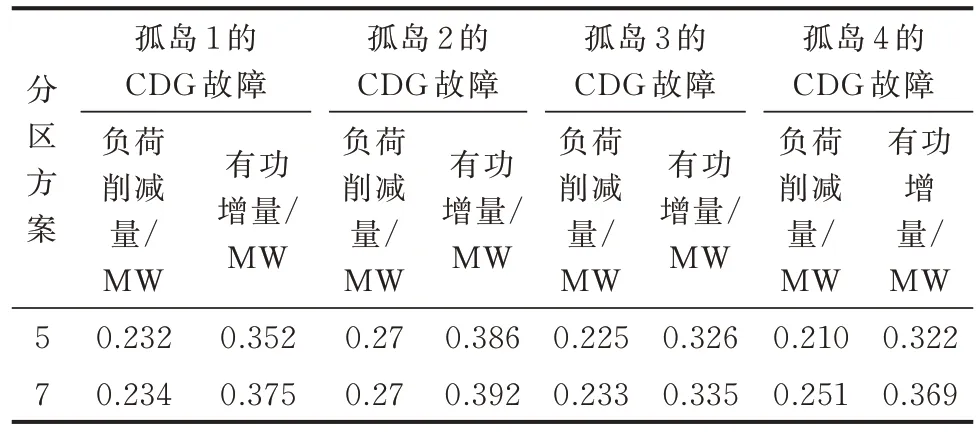
表2 方案集2 各方案4 种CDG 故障下各自应对策略Table 2 Coping strategies for four types of CDG faults for each scheme in scheme set 2

虽然由附录A 表A4 中的总处理策略成本可知，方案5 和7 的总成本都较低，但是本着优先考虑用户负荷的原则，方案5 中除了孤岛1、2 的CDG 故障时负荷总削减量基本一致外，孤岛3、4 的CDG 故障时方案5 的负荷总削减量显著低于方案7。

5 结语

本文提出的基于潮流追踪的VM 分区规划方法在评估各区域能源利用率、内外源荷连接强度整体性、故障下闭合线路开关后的处理策略均作出了相应的研究。在算例部分中，本文将IEEE 33 节点模型的8 种分区方案通过双层分区规划模型进行层层筛选，优先考虑基于潮流追踪模块度最大和孤岛内部电压质量分布最优，其次考虑故障应对策略成本，筛选出了两种更合理的分区方案：

1）在筛选过程中分别为各分区配置了CDG 以及制定了各台CDG 故障下的应对策略。

2）对两种优选方案进行了进一步的对比，得出了后者正常运行状态下区域内CDG 利用率更高，而前者在故障下用户负荷削减的体验方面更佳的结论。二者均为正确而有效的分区方案。

合理的VM 分区对于提高系统稳定性、优化能源利用、降低运营成本和方便管理维护等方面都具有极大的意义。但在本文的研究中，对于分区场景的考虑仍较为单一，下一步将考虑多场景下的分区规划。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。