应用型本科高校线性代数全英语课程建设探索
2024-01-18郭琼
摘 要:当今世界对国际化人才的需求日益增长,高等教育的国际化水平亟待提高。线性代数作为国际上几乎所有高等院校的理工科专业均开设的课程,国际化资源丰富,课程应用性强,非常适合应用型本科高校进行全英文教学开展。该线性代数全英语课程的建设以培养学生的数学素养、实践能力、国际化视野和家国情怀为教学目标,依托雨课堂平台开展融入思政元素的线上线下混合式教学改革。
关键词:线性代数;全英文教学;混合式教学;课程思政;应用型本科
中图分类号:G642 文献标志码:A 文章编号:2096-000X(2024)02-0084-04
Abstract: Along the increasing demanding on the international talents over the world, the internationalization of high education needs to be improved urgently. As a course offered by science and engineering majors in almost all international universities, linear algebra course has abundant international resources and a lot of application-oriented projects, which is very suitable for application-oriented universities to be set as an English medium instruction course. In order to cultivate the mathematical thinking ability, practical ability, international vision, and home country feelings for the students, blended teaching model based on Rain Classroom platform combined with the ideological and political materials, will be conducted.
Keywords: Linear Algebra; English medium instruction; Blended teaching model; curriculum ideology and politics; application-oriented university
随着当今世界国际化交流与合作日益频繁,人才培养的国际化水平越来越受到重视。《国家中长期教育改革和发展规划纲要(2010—2020年)》中提出应加强国际交流与合作。坚持以开放促改革、促发展。开展多层次、宽领域的教育交流与合作,提高我国教育国际化水平;借鉴国际上先进的教育理念和教育经验,促进我国教育改革发展,提升我国教育的国际地位、影响力和竞争力。适应国家经济社会对外开放的要求,培养大批具有国际视野、通晓国际规则、能够参与国际事务和国际竞争的国际化人才[1]。全英教学作为培养具有国际竞争力的高素质人才的有效途径,正在被越来越多的高校所采用,这对中国推进世界一流大学和一流学科的建设有着重要作用和意义[2]。
上海应用技术大学,是中国第一所以“应用技术”命名的应用型本科院校,致力于建设具有国际影响力的高水平应用创新型大学。学校非常重视国际交流,与欧洲、美洲、亚洲和大洋洲等20多个国家(地区)的120余所高校和科研机构建立了交流合作关系,设有多个本科中外合作办学项目。学校开设多个全英语专业,积极探索国际化应用创新型人才的培养。笔者所授线性代数(Linear Algebra)全英文课程是2020年度立项的上海高校市级重点课程建设项目,其授课对象为上海应用技术大学和美国中央密西根大学(Central Michigan University)合作办学的全英语本科专业——机械设计制造及其自动化专业的大学二年级第一学期学生。该中外合作专业从2003年開始招生,通过合作办学项目的开展,加强国内外高校间的相互交流,为机械类行业/企业应对国际竞争提供人力支持[3]。根据上海市教委立项要求,示范性全英文课程应以提升学生的国际视野、人文素养、跨文化交流和学术交流能力为培养目标,以国际同类一流专业核心课程为参照,选用经审查合格的国外优秀原版教材作为主要教材,教学理念和教学方式先进,教学团队结构合理、外语水平高,形成示范辐射作用。本课程根据上述要求在教学目标、教学内容、教学手段和方法,以及课程评价模式上进行改革和创新,且课题组成员均有欧美国家留学或访学经历,具有优秀的英语素养,能很好地胜任全英语教学,并能在课程中适时融入欧美先进的教学手段、方法和教学案例,有利于开阔学生的国际化视野。
一 课程教学目标
国际上几乎所有高等院校的理工科专业都开设有线性代数课程,它从解线性方程组和讨论二次方程的图形等问题发展起来,随着计算机科学和信息技术的日新月异,而广泛应用于自然科学、社会科学及工程技术等领域。上海应用技术大学理工科各专业的本科生培养计划中均开设有线性代数课程作为学科大类基础课之一。特别对于机械设计制造及其自动化专业,线性代数课程在解决机械系统设计、工艺设计和机电控制与测试等复杂工程问题中发挥重要作用。此外,该课程先修课程仅为高中数学,因此将其作为该全英语专业学生的第一门非语言类全英语课程,学生的接受程度会较高,同时也为学生后续全英语专业课程的学习作了良好的铺垫。
线性代数全英文课程的教学目标是使学生在掌握常用的矩阵方法、线性方程组、特征值与特征向量等基本概念、理论和计算的基础上,具有建立合理的数学模型分析和解决一些简单工程实际问题的能力,使用计算机软件MATLAB简化复杂计算的能力;以及让学生掌握基本的数学专业词汇、数学符号和公式的表达,适应全英语教学形式,为后续全英语专业课程的学习奠定必要的基础;同时,通过思想政治教育元素和跨国文化的有机融合,培养学生的人文素养和家国情怀;力争实现创新型、应用型、复合型人才的培养目标。
二 课程教学探索
《国家中长期教育改革和发展规划纲要(2010—2020年)》指出,应创新人才培养模式,注重学思结合:倡导启发式、探究式、讨论式、参与式教学,帮助学生学会学习;注重知行统一:坚持教育教学与生产劳动、社会实践相结合。注重因材施教:关注学生不同特点和个性差异,发展每一个学生的优势潜能[1]。此外,习近平总书记2016年在全国高校思想政治工作会议上指出,要坚持把立德树人作为中心环节,把思想政治工作贯穿教育教学全过程[4]。上海应用技术大学自2017年起着力将思政改革应用在教学实践中,并于2019年入选上海市高校课程思政整体改革领航高校。此前课题组成员已对上海应用技术大学高等数学课程进行过课程思政的教学探索与实践[5-6]。此次,如何在线性代数全英文课程中创新教学模式并努力实现“盐融于汤”的课程思政融合教学,是本课程建设的重点。
(一) 教材及拓展资源选用
本课程选用StevenJ.Leon教授撰写的优秀全英文教材Linear Algebra with Applications,国内外有许多高校选择此教材进行授课。该教材遵循线性代数的发展历史,从学生在高中阶段已熟知的简单线性方程组出发,引入线性方程组的一般形式,将一般形式进行简化则得到本课程的主要研究对象——矩阵。再以矩阵为工具介绍复杂线性方程组求解的一般方法,然后进行矩阵的一系列其他应用的介绍。从已有知识到新知识再到知识在工程中的应用的编写逻辑,学生易于接受;同时,该教材加入许多直观的几何图形进行辅助,让学生对抽象的数学知识点有更直观的理解,有利于学生掌握数形结合的数学思维方法。此外,该教材每个章节中均包含有计算机软件MATLAB实践项目,能有效训练学生将数学理论、工程案例、计算机软件相互结合的能力,有利于实现学以致用的能力目标。
鉴于学生第一次接触全英语的非语言类课程,为其提供拓展资源作为补充非常重要。本课程拓展资源将依据当代学生网络“原住民”的特点,以及应用创新型人才的培养目标,选用互联网中优秀的英文视频资源及相关工程应用案例的中英文文献,供学生在课堂外进行自主学习及在课堂内利用拓展资源进行翻转课堂教学。
(二) 教学方法和手段
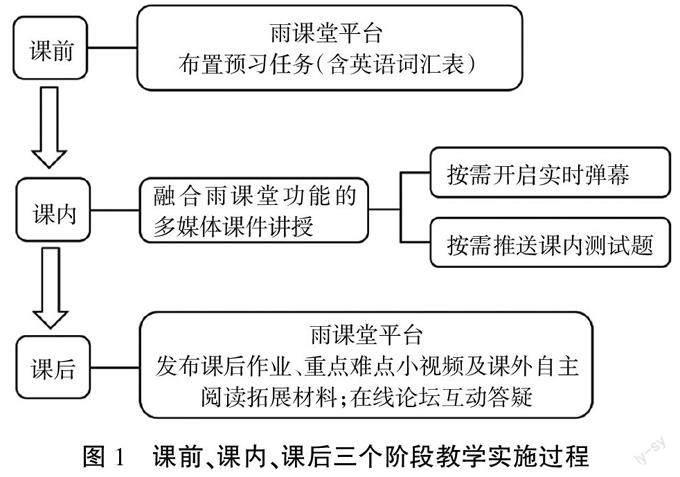
本课程从创新人才培养模式的角度出发,采用加涅九步教学法、启发式教学法和案例教学法进行教学,并适时融入思政元素,同时培养学生的人文素养和家国情怀。从学生感兴趣的社会热点、生活实例、经典的应用案例或其已掌握的知识点入手,引起学生注意,提出问题,激发学习动机并呈现知识、能力和思政学习目标。通过启发学生思考的方式,引导学生借助已有知识获取新知识。围绕新的知识点补充例题或工程案例,引导学生跟随分析思考和解决问题。实时发送课内测试题检测教学效果,收到反馈后及时调整教学节奏。最后总结本节课所学的新的知识点,布置相关作业,并给出课后复习及拓展阅读材料促進教学内容的保持与迁移。以上教学方法的使用目的在于激发学生学习兴趣,提高学生课堂教学参与度和课外自主学习的能力。为了更好地达到这一教学目的,本课程采用雨课堂平台开展混合式教学,分为课前预习、课内互动、课后复习拓展答疑三个阶段进行,如图1所示。具体实施过程如下。
1 课前阶段——旧知沉淀,新知预告
课前在雨课堂平台发布预习课件。针对本课程全英语授课的特点,预习课件应主要包含两部分内容。
1)英语词汇的复习和预习。例如,可以在课件中设置词汇闯关题,学生答题完毕后平台自动批改,答案全部正确则为闯关成功,否则可以重新答题。通过这种方式减少全英语教学过程当中因语言问题而引起的理解障碍,同时雨课堂后台的数据记录能帮助师生双方及时掌握认知情况。
2)教学内容预告。主要采取以下两种方式:利用学生喜欢观看短视频的特点,在预习课件中插入与课程相关的网络视频或自制视频激发学生兴趣。例如,在第三章向量空间(Vector Spaces)的首次课前,可以发布bilibili网站全英文视频(中英文双语字幕)“从一维到十维”(https://www.bilibili.com/video/BV12x411Y7J7/?spm_id_f
rom=333.788.videocard.0),视频中既包含了本章向量空间中的大部分英语词汇,也渗透了数学领域中一种常见的思维模式:从特殊到一般,启发学生如何从低维空间的定义中抽象、凝练出使用数学语言描述高维空间的一般表达形式,并引发学生去思考高维与低维的相同与不同之处;注重应用反哺教学,在预习课件中发布有趣的应用案例,让学生在阅读完后再结合MATLAB计算机软件完成给定的任务,并要求学生根据任务完成情况形成一个小报告,用于课内进行翻转课堂教学。例如,在第一章第四节矩阵代数(Matrix Algebra)课前可以给出产品成本模型应用案例。虽然学生可以借助以往的数学知识解决该应用实例,但是如何使用矩阵简化计算是希望学生去探究的内容。课件中可以提示学生如何将所构造的数学模型表示为矩阵的形式,然后让学生借助MATLAB去探索利用矩阵的乘法解决该问题,并将其探索结果写成小报告,供课内进行翻转课堂教学时使用。事实上,在翻转课堂实施过程中,我们发现不同的学生会对该应用案例有不同的探索方式,从而对如何进行矩阵乘法的计算也会有自己不同的理解。不同学生间思想上碰撞出的火花让其实践创新能力得到了进一步提升。
2 课内阶段——掌握新知,内化思政
课内教学的实施中应以学生感兴趣的生活实例或工程案例引入,以问题为驱动,借助多媒体教学生动、形象、直观的动画和视频表现形式帮助学生理解抽象的数学概念,加强学生的感性认识,并充分发挥雨课堂平台的各项功能,更好地实施混合式教学。例如,按需开启学生喜欢的雨课堂弹幕功能,让因害羞或其他原因不愿意提问的学生能有实时反馈的渠道;合理设计融合雨课堂版的多媒体课件,阶段性地通过雨课堂平台抛出合适的题目,实时检测学生对讲授知识的理解和接受程度,明确学生需求,实时调整教学节奏。同时,适时融入课程思政教育元素,从科学知识中积累人文素养和培养家国情怀。在数学理论的应用上,多选取与专业背景相关的实例进行训练,增强学生的实际应用意识,培养学生的创新意识,引导学生借助于数学软件MATLAB来解决较复杂和繁琐的计算问题。现以第三章向量空间(Vector Spaces)第二节线性无关(LinearIndependence)为例。
1)教学引入(思政元素融入)。生活中的相关:从三原色中构造五彩缤纷的世界。用数学公式描述任意颜色。哲学中的相关:“天才是1%的灵感+99%的汗水”“好的开始是成功的一半”。用数学公式表达哲学谚语;数学中的相关:回忆已有的二维向量共线、三维向量共面的数学表达。
2)启迪新知(类比法教学)。引导学生对上述三个引例进行类比,并自主提炼“相关”这两个字的数学内涵。教师总结点评学生发言并给出“向量线性相关”的准确定义。给出相关例题,加深对概念的理解。例题讲解过程中实时发布课内测试题检测学习效果,实时调整授课节奏。
3)思维拓展(思政内化及应用延伸)。数学思维拓展。和学生一起回到课程开始的数学引例,重述线性相关和无关在低维时的几何意义,再次强调数学中从特殊提炼到一般的抽象思维方式。思政内化拓展。生活中的相关引例可以提升为和谐社会需要每一位公民的努力,世界和平需要每一个国家的支持,抗击疫情人人有责等,培养学生的家国情怀,以及为全世界人民造福的大爱精神。总结与工程应用拓展。小结本节课知识点,并通过雨课堂开启弹幕引发学生讨论线性相关和无关这一数学概念在工程中的应用。
3 课后阶段——知识巩固,应用实践
课后主要由复习及拓展课件推送和在线互动答疑两部分组成。
1)复习及拓展课件推送。主要包含课后书面作业、MATLAB软件操作验证、自制全英语重难点小视频让学生再次对本次课的重点难点进行记忆和练习,同时适当加入网络视频资源或文献拓展阅读,为学有余力的同学拓宽知识面,开阔眼界。例如,在上述第三章第二节线性无关的课后可推送可汗学院的短视频:More on linear independence(https://www.khanacademy.org/math/linear-algebra/vectors-and-spaces/linear-independence/v/more-on-linear-independence)作为对此节课教学的有益补充;并可让学生自主试验如何使用MATLAB判断一组向量是否线性相关。
2)在线互动答疑。互动答疑形式不局限于“师生互动”,更鼓励“生生互动”。学生之间互相分享自己的想法共同提高,往往也能擦出思想上的火花,这同样也是一种课程思政。例如,在课程实施中,关于线性相关与无关这一知识点,可设置课后线上平台的分组讨论,让学生课后自主搜集探索其在工程案例中的实际应用与意义,每个小组需将本组的成果总结成一个5分钟以内的小报告,在下一次课前与大家分享。该形式的讨论和总结本质上是对所学知识进行拓展应用,有利于提高学生文献搜索、团队合作、语言表达以及创新实践的能力,这不仅对后续教学内容的开展大有帮助,也对日后的专业学习有着重要意义。
三 课程考核评价模式
本课程采用过程性评价,即考核贯穿于整个学习过程,综合评价其对知识的掌握和运用情况。具体由以下三部分组成。
雨课堂平台数据(占比20%):包括考勤、课前预习、课内小测试答题和课后作业等。
实践应用考核环节(占比30%):包括课内小报告和MATLAB小型课程设计两部分。
期末笔试(占比50%):全面覆盖课程所有章节中的数学知识点与相关应用案例,全英文试卷,要求全英文作答。
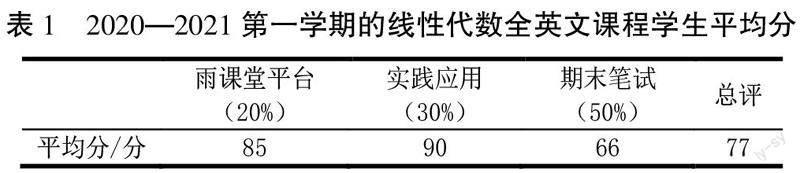
表1为上海应用技术大学机械设计制造及其自动化专业(全英语专业)2020—2021第一学期的线性代数全英文课程三部分考核内容的学生平均分。
由表1可知,学生在本课程线上线下混合式教学各环节中的配合度较高,在以其自身为主导的实践环节中表现较好。笔试部分虽然采用全英文试卷并要求学生全英语作答对学生有一定的难度,但整体来看,学生对该课程的知识点掌握良好,基本达到该课程的预期目标。
目前,雨课堂平台上已建成线性代数(Linear Algebra)课程的教学资源库,包括全程教学视频、教学大纲、授课计划、教学课件、预习课件、复习课题库、重点难点微视频、拓展阅读视频及文献、课程交流和答疑园地等丰富的内容。借助雨课堂平台突破了时间与空间的限制,提高了学生的学习效率,培养了学生自主学习的能力,既实现了知识的保持,也为学有余力的同学实现了拓展知识的提升。
四 课程总结与展望
随着我国“一带一路”倡议的提出,世界对国际化人才的需求日益增加。因此,提升高等教育国际化水平是我国各大高等院校不可推卸的责任。线性代数作为高等院校理工科各专业的一门重要数学基础课,教学重点在于为后续各专业课程打下坚实的数学基础,以及提高学生的逻辑思维能力和创新实践能力。目前,许多优秀的、经典的工程案例和科学技术均来自欧美等发达国家,因此,将此课程设置为全英文课程有利于学生国际化视野的培养以及后续专业课的学习;从教学形式上看,融入思政元素的线上线下混合式教学模式既符合当代学生网络原住民的特点,也培养了学生的文化自信和家国情怀。从教学效果看,学生通过本课程学习掌握了必要的线性代数知识点,锻炼了建立数学模型并应用计算机软件解决实际应用问题的能力,并一定程度上提高了语言表达和团队合作的能力。笔者认为,该全英文课程可推广性较强,在现有网络教学资源库的基础上,不断补充丰富各专业领域相关应用案例和思政元素,则可很好地融入其他工科专业的培养计划,对培养具有开放的国际视野、坚定的理想信念、过硬的人文和科学素养的应用创新型人才具有重要的现实意义。
参考文献:
[1] 中华人民共和国教育部.国家中长期教育改革和发展规划纲要(2010—2020年)[EB/OL].http://www.moe.gov.cn/jyb_xwfb/s6052/moe_838/201008/t20100802_93704.html.
[2] 段丹阳.全英教学研究综述[J].高等建筑教育,2017,26(4):94-99.
[3] 尚慧琳,张涛.国际化背景下理论力学全英文教学实践与探索[J].大学教育,2019(7):47-49.
[4] 习近平在全国高校思想政治工作会议上强调:把思想政治工作贯穿教育教学全过程 开创我国高等教育事业发展新局面[N].人民日報,2016-12-09(001).
[5] 郭琼,张雯莹,王凤超.新工科背景下高等数学案例教学与课程思政的融合探索[J].科教文汇(上旬刊),2021(10):51-52.
[6] 张雯莹,郭琼,王凤超.基于课程思政的高等数学课程的教学设计——以《定积分的概念》为例[J].教育现代化,2021,8(23):157-161.
