宽带噪声激励下分数阶黏弹性碰撞系统的稳定性分析和随机分岔
2024-01-17盛正大张建刚
盛正大, 张建刚, 王 媛
(兰州交通大学 数理学院, 兰州 730070)
在实际工程应用中, 由于存在摩擦、 形变和材料间隙等不同干扰因素, 使工程中的应用材料经常发生碰撞, 这些不可避免的碰撞导致工程系统不稳定. 因此研究实际工程中存在的非线性碰撞动力学问题, 深入了解工程系统动态特性具有重要意义: 首先可避免碰撞现象导致的损失; 其次可提高工程系统的工作效率并延长其使用寿命等. 由材料间隙、 冲击、 干摩擦和不可微刚度等非光滑因素导致的碰撞动力学问题具有强非线性[1-2]: 文献[3-4]根据动力系统理论研究了碰撞振动系统的动力学行为; Nordmark[5-6]利用局部映射方法研究了碰撞系统特有的擦边分岔现象; Luo等[7-8]采用数值模拟发现碰撞系统存在Torus分岔和Hopf分岔的动力学现象; 李群宏等[9-10]分析了碰撞系统的稳定性条件和判据, 并得到有关单碰周期n次谐运动的存在性判据依据和稳定性条件. 对于随机激励下的碰撞系统, Dimentberg等[11-13]将碰撞系统转化为无碰撞的非光滑系统, 分析了随机碰撞系统的响应问题; Jing等[14-15]研究了高斯白噪声作用下的单自由度碰撞系统, 并获得了概率密度的解析解.
近年来, 黏弹性材料在汽车和航天等工程领域应用广泛, 根据其黏性和弹性两种机理制成的阻尼器在减振储能等方面具有优良表现. 因此研究基于黏弹性材料构建的碰撞模型, 在减振和隔振等工程领域具有重大意义. 徐伟等[16]研究了黏弹性对系统的两种效应: 经典阻尼效应和刚度效应; Xu等[17]从正弦输入为起点, 推演出黏弹性阻尼器关于能量耗散的算法; Zhu等[18]介绍了随机平均法与能量包络平均法在黏弹性动力系统中的应用.
实际工程应用中黏弹性材料可将结构间的振动转化为热能, 从而抑制结构振动. 分数阶导数具有描述各种过程记忆和遗传特性的优越性, 分数阶项可较好描述系统历史发展的依赖过程, 在描述复杂的物理问题时配合非线性模型, 表述更简洁且更贴近真实的物理本构关系[19-21]. 目前对随机激励下基于分数阶黏弹性材料构造的约束碰撞系统的研究文献报道较少, 基于此, 本文基于Kelvin-Voigt材料的分数阶本构模型构造黏弹性Van der pol减振模型, 并分析在宽带噪声激励下系统的随机稳定性和随机分岔行为[22-24].
1 构建模型
黏弹性材料Kelvin-Voigt的分数阶本构模型[21]为
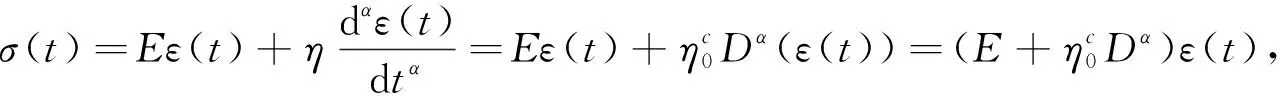
(1)
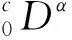
将宽带噪声激励下的具有黏弹性材料阻尼的单自由度非线性碰撞系统写为

(2)
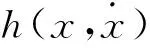

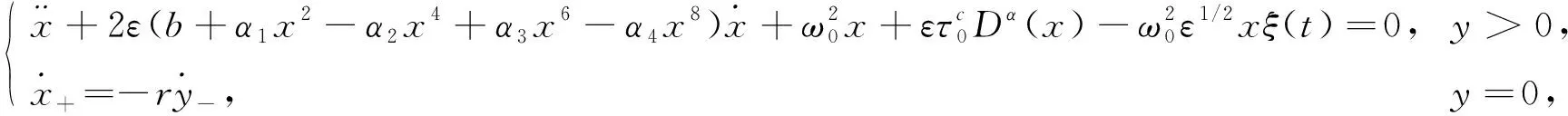
(3)
其中τ=η/E表示黏弹性参数.通过非平滑Zhuravlev变换, 将系统(3)转化为
2 随机平均法
设φ(t)=ω0t+θ, 令式(4)的解为

(5)
可得

(6)
将式(6)和式(5)联立, 可得

(7)
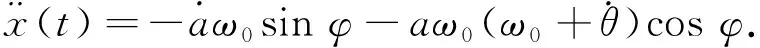
(8)
将式(5)和式(8)代入系统(4)中, 可得

(10)
其中

(11)
因此将Caputo形式的分数阶微分Dαx(t)写成双积分形式
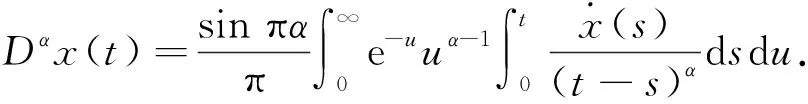
(12)


(13)
则式(13)满足
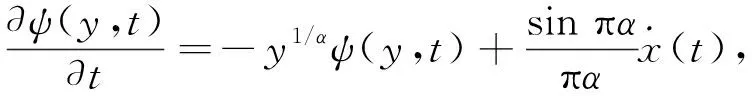
(14)
将式(5)代入式(14)可得

(15)
解得
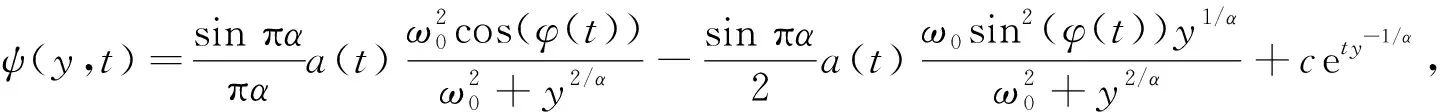
(16)
其中c根据初始条件ψ(y,0)=0决定.将式(16)代入式(13)可得
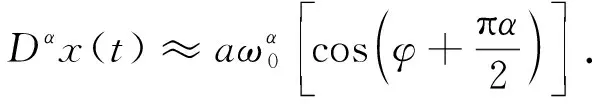
(17)
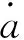

(18)
由于a(t)和θ(t)为时间慢变量,φ(t)为快变量, 因此经随机平均和确定性平均后, 所得漂移系数和扩散系数为
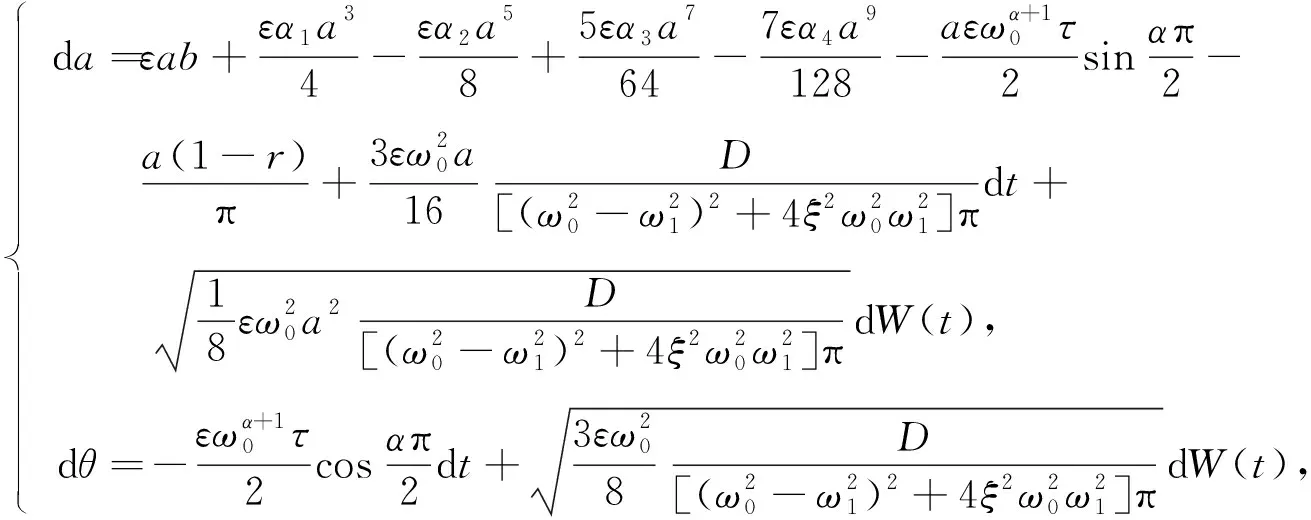
(19)
其平均振幅
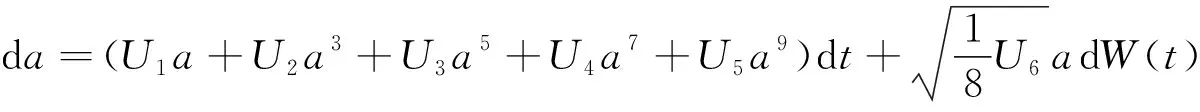
(20)
是一维Markov过程, 其中
3 随机稳定性
3.1 局部稳定性
讨论U2=U3=U4=U5=0, 将式(20)变换为
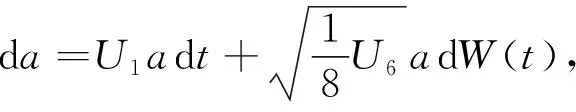
(21)
其中m(0)=U1,σ(0)=(U3/8)1/2.可得线性It随机微分方程Lyapunov指数近似解为
系统的局部稳定性分析列于表1.

表1 系统的局部稳定性分析
3.2 全局随机稳定性
讨论当U2=U3=U4=U5=0时的线性It随机微分方程, 将式(20)变为式(21),a=0时是系统的第一类奇异边界, 扩散指数αr=2, 漂移指数βr=1, 可得特征标值
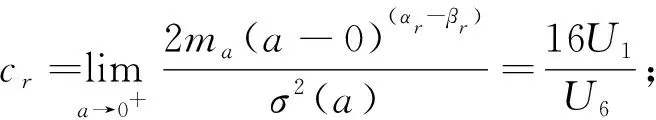
(22)
a=+∞时是系统的第二类奇异边界, 扩散指数αl=2, 漂移指数βl=1, 可得特征标值
表2 在线性It随机微分方程条件下系统的全局随机稳定性
Table 2 Global stochastic stability of system under condition of linear It stochastic differential equation

表2 在线性It随机微分方程条件下系统的全局随机稳定性
状态条件类别状态条件类别r=0cl>1, U1/U6>1/16排斥自然边界r=+∞cl>-1, U1/U6<1/16排斥自然边界cr=1, U1/U6=0严格自然边界cl=1, U1/U6=0严格自然边界cr<1, U1/U6<1/16吸引自然边界cl<-1, U1/U6>1/16吸引自然边界
讨论Um不全为0的情况, 其中m=2,3,4,5.a=0时是系统的第一类奇异边界, 扩散指数αr=2, 漂移指数βr=1, 可得特征标值为式(22).a=+∞时是系统的第二类奇异边界, 扩散指数αl=2, 漂移指数βl为式(20)中所有Um≠0项幅值a的最高次数, 可得特征标值为
Un为式(20)中系数不为0且有关幅值a最高次数项的系数, 根据奇异边界理论可得在非线性It随机微分方程条件下系统的全局随机稳定性, 结果列于表3.
表3 在非线性It随机微分方程条件下系统的全局随机稳定性
Table 3 Global stochastic stability of system under condition of nonlinear It stochastic differential equation

表3 在非线性It随机微分方程条件下系统的全局随机稳定性
状态条件类别状态条件类别r=0cl<1, U1/U6<1/16吸引自然边界r=+∞cl<-1, Un/U6>1/16吸引自然边界cr=1, U1/U6=1/16严格自然边界cl=-1, Un/U6=1/16严格自然边界cr>1, U1/U6>1/16排斥自然边界cl>-1, Un/U6<1/16排斥自然边界
由表3可见, 当r=0为吸引自然边界,r=+∞为进入边界, 可理解为左边界为吸引自然边界, 而在右边界未进入时, 平衡点处于全局稳定.根据局部稳定性条件可得, 在满足U1/U6<1/16,Un/U6<1/16的条件下, 系统在平衡点处保持稳定状态.
4 随机分岔分析
4.1 D-分岔

(23)
当m(0)=0,σ(0)=0时, 0为φ的一个固定点, ∘dW为Stratonovich随机过程的参激.设m(r)有界,a≠0系统有且只有一个稳态概率密度, 幅值a(t)对应的FPK(Fokker Planck Kolmogorov)方程为

(24)
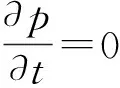
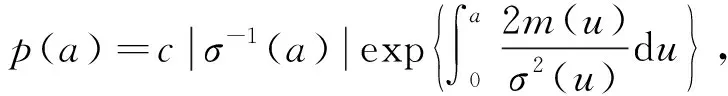
(25)
得到式(23)存在不动点和非平凡平稳运动两种平稳状态.δx为不动点的不变测度δ0, 式(25)为非平凡平稳运动状态的不变测度的密度.
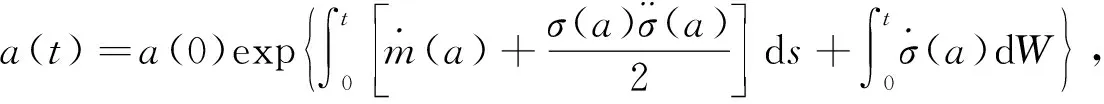
(26)
φ关于测度μ的Lyapunov指数定义为
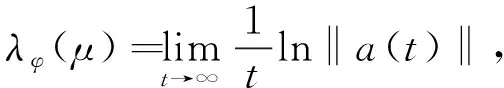
(27)

使α=U1-U6/16, 可得不动点不变测度δ0在α≤0处是稳定的, 非平凡状态不变测度在α>0处是稳定的, 则α=0是一个D-分岔点.
将式(24)化简为
pst(a)=ca2(8U1-U6)/U6=o(av)a→0,
其中c为归一化常数.设v=2(8U1-U6)/U6, 当v<-1时, 即16U1/U6<1,pst(a)为δ函数; 当-1
4.2 P-分岔
W(t)是标准的Wiener过程, 且da不依赖于θ, 因此可得系统幅值的FPK方程为
其中
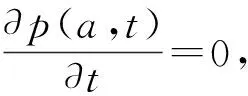
其中C为归一化常数.
稳态概率密度函数的精确表达式为
4.2.1 分数阶阶次α对系统随机分岔的影响
设添加的外部噪声各系数值ζ=1,ω0=0.9,ω1=0.1和噪声强度D=7, 固定系统的参数值α1=1.51,α2=2.85,α3=1.693,α4=0.312, 选取系统黏弹性参数τ=0.8和黏弹性材料的恢复系数r=0.9.改变系统(4)分数阶次的数值, 绘制相应的稳态概率密度函数曲线.
固定噪声和系统的其他参数, 仅改变分数阶阶次, 乘性宽带噪声激励下不同分数阶次的稳态概率密度函数曲线如图1所示.由图1(A)可见, 在稳态概率密度函数曲线上距离原点较远处有一个明显峰值, 系统是单稳的, 仅存在大幅振动. 由图1(B)可见, 当α=0.5时, 稳态概率密度峰值发生变化, 在稳态概率密度函数曲线上距离原点较远处有一个明显峰值, 但在原点附近为Dirac函数形式, 幅值的稳态响应为0, 此时系统存在两种运动状态. 因此, 当分数阶次改变时, 稳态概率密度函数的定性也随之改变, 系统产生随机P-分岔.

图1 乘性宽带噪声激励下不同分数阶次的稳态概率密度函数曲线Fig.1 Steady state probability density function curves of different fractional orders under multiplicative broadband noise excitation
4.2.2 宽带噪声强度变化对随机分岔的影响
将分数阶阶次固定为α=0.5, 改变噪声强度D值, 其他参数与图1相同, 绘制相应的稳态概率密度函数曲线.
固定分数阶次和系统的其他参数, 仅改变外部宽带噪声的噪声强度, 乘性宽带噪声激励下不同噪声强度的稳态概率密度函数曲线如图2所示.由图2(A)可见, 当D=3.1时, 稳态概率密度曲线为Dirac形式, 系统幅值的稳态响应为0, 类似一个稳定平衡点; 由图2(B)可见, 当D=5.3时, 在稳态概率密度函数曲线上距离原点较远处有一个明显峰值, 但在原点附近为Dirac形式, 此时系统存在两种运动状态; 由图2(C)可见, 当D=9.8时, 在稳态概率密度函数曲线上距离原点较远处有一个明显峰值, 系统存在大幅振动. 因此, 当改变外部噪声强度时, 稳态概率密度函数的定性也随之改变, 系统产生随机P-分岔.
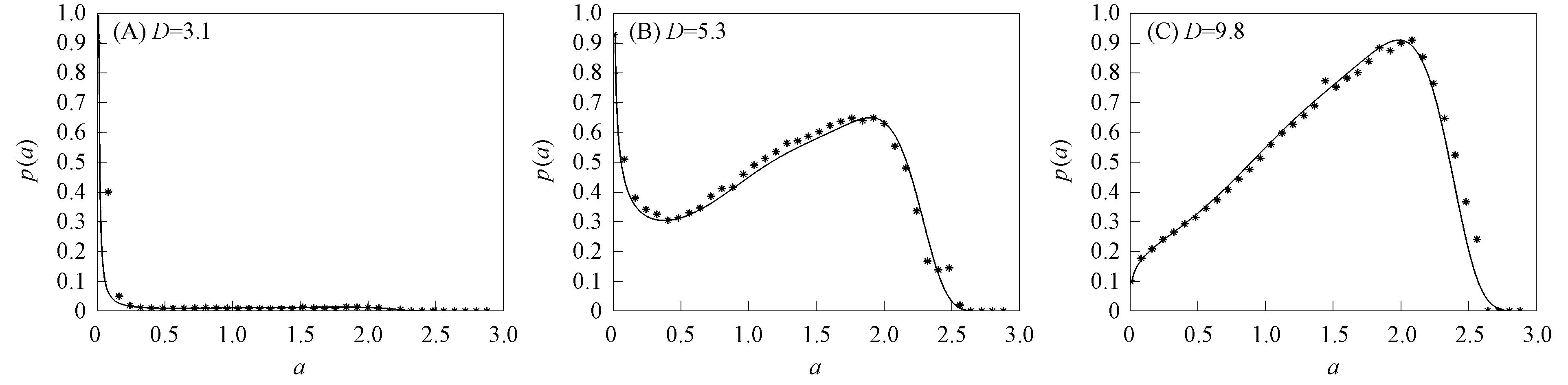
图2 乘性宽带噪声激励下不同噪声强度的稳态概率密度函数曲线Fig.2 Steady state probability density function curves of different noise intensities under multiplicative broadband noise excitation
综上, 本文研究了对外部宽带噪声激励下的基于分数阶黏弹性材料的Van der pol减振系统, 通过随机平均法求出了系统的It微分方程. 利用最大Lyapunov指数法和奇异边界理论分类讨论了系统的局部随机稳定性和全局随机稳定性. 通过拟Hamilton系统随机平均法分析了系统在线性It微分方程情形下的D-分岔行为, 得到了系统产生D-分岔的临界条件, 并对分数阶阶次α和宽带噪声强度D分别改变的情况进行数值模拟. 结果表明: 在宽带噪声的激励下, 固定其他参数不变, 仅改变分数阶阶次α值, 稳态概率密度函数曲线出现定性变化, 系统产生了随机P-分岔行为; 改变宽带的噪声强度D, 稳态概率密度函数曲线也出现定性变化, 系统随强度值的变化产生P-分岔行为.
