动态自触发通信下多智能体输出反馈包容控制

左仁伟, 李颖晖,*, 吕茂隆, 聂鸿雁

(1. 空军工程大学航空工程学院, 陕西 西安 710038; 2. 空军工程大学空管领航学院, 陕西 西安 710051;3. 中联西北工程设计研究院有限公司, 陕西 西安 710077)

0 引 言

多领导者包容控制是近年来多智能体协同控制领域的研究热点之一,其主要任务是通过设计控制协议,驱使一组跟随者运动至多个领导者所围成的最小几何空间(凸包)中[1]。包容控制可有效规避复杂危险环境中的动态障碍物干扰,显著提高任务执行效率和系统安全裕度,在多智能体遂行敌区搜索、火灾营救以及合作运输等任务中有着广阔应用前景[2-3]。然而,实际网络化多智能体对信道带宽和传输频率有着较高要求。当信号传输通道带宽受限、智能体之间交互频繁时,网络通信可能出现信号阻塞/数据丢包等不利情形,严重降低控制系统的实际运行性能。为在有限通信资源的基础上保证群系统安全稳定运行,学者们提出以事件发生来驱动信号传输的事件触发通信机制[4-6]。相比传统采样周期固定的时间触发通信机制,事件触发通信机制具有网络通信频次低和信道带宽占用小等优势,因而广泛应用于航天器组网[7]、智能电网[8]、自动驾驶汽车编队[9]、高速列车协同[10]等实际系统。

值得注意的是,上述成果[4-10]均属于静态事件触发通信机制,即基于静态触发函数解算下一信号传输时刻,其系统能耗与带宽占用相对较高。为进一步放宽事件触发阈值,Girard在静态事件触发机制(static event-triggered mechanism, SETM)的基础上提出一种动态事件触发机制[11](dynamic event-triggered mechanism, DETM),该机制的关键特征是触发函数包含一个额外的内部动态变量,其动态可被视为静态触发函数的滤波输出。相比于SETM,DETM具有更大的事件触发阈值和更少的信号传输频次,因而吸引了大量学者关注;Ge等为调度智能体间的通信,开发了一种动态事件触发通信机制,减少了智能体间不必要的数据交换,获得了更高的通信资源利用效率[12];Ahmad等针对配备动态阻尼器的轮毂式电动汽车,研究了分布式动态事件触发通信和主动悬架控制的协同设计问题[13];Coutinho等采用协同设计方法,同时设计DETM和增益调度控制器,并利用状态相关的调度函数对控制器进行参数化[14]。然而,上述事件触发机制均要求智能体连续监测系统状态信息,以便实时判断是否满足触发条件,在一定程度上会造成传感器资源浪费。

为进一步放松该限制条件,Anta等提出一种无需连续监测系统状态信息的自触发机制,该机制只需目标当前状态信息即可解算下一采样时刻,并在该时刻进行状态测量、控制律计算、执行器更新[15]。在文献[15]的基础上,自触发机制被大量应用于线性系统[16]、非线性系统[17]、线性多智能体[18-20]以及非线性多智能体[21-23]的控制设计中;Wang等扩展了传统自触发反馈系统L2稳定性的相关工作,基于采样状态预测下一事件的开始和完成时间,放宽了传统工作中过程噪声幅值受系统状态限制的假设条件[16];Wang等设计了一种能够有效补偿输入迟滞非线性的自触发控制方法,保证跟踪误差由设计参数的显式函数限定[17];Xu等构建了一种完全分布式自触发机制,在线调度每个线性智能体网络信道的信息传输[20];Chen等针对一类传感器饱和情形下的非线性多智能体,提出了一种基于神经网络的自触发一致性控制方案[21]。上述文献工作为推进研究自触发通信机制下高阶不确定非线性多智能体协同控制问题提供了坚实的理论基础。然而,以上工作在设计事件触发机制时没能综合考虑动态事件触发和自触发机制的优势[24-26]。如何设计一种无需连续监测系统状态信息且触发阈值较大的动态自触发通信机制是目前亟需解决的关键难题。

鉴于此,本文在DETM[11-14]和自触发机制[15-23]的基础上提出一种新型动态自触发通信机制,在具有更大触发阈值的同时无需连续监测系统状态信息,进一步减少对网络带宽、通信成本以及智能体自身能量等有限资源的不必要消耗;采用径向基神经网络(radial basis function neural networks, RBFNNS)在线逼近系统不确定项,并设计自适应律实时更新网络权值信息;利用高增益观测器在线估计系统全状态变量,并在此基础上构建一种输出反馈多领导者包容控制协议,驱使所有跟随者收敛到领导者所围成的动态凸包中,同时保证闭环系统所有信号半全局一致终结有界(semi-globally uniformly ultimately bounded, SGUUB)。

1 预备知识及问题陈述

1.1 代数图论

本文利用有向图G(V,ε)刻画N+M个智能体的通信拓扑,其中V∈N1:N+M表示节点集,ε⊆V×V表示边集,i∈N1:n表示i=1,2,…,n。若智能体j能够接收到智能体i的信息,则记(i,j)∈G。记智能体i的邻域为Ni{j/(j,i)∈ε}。定义图G对应的加权邻接矩阵为A[aij]∈R(N+M)×(N+M),当(j,i)∈ε时aij>0,当(j,i)∉ε时aij=0。假设节点不存在自环,即aii=0。定义图G的度矩阵为Ddiag[Di]∈R(N+M)×(N+M),式中Di=∑j∈Niaij。定义图G对应的Laplacian矩阵如下:

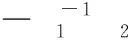
1.2 问题陈述

考虑具有N+M个节点的高阶非线性多智能体,其中节点1,2,…,N表示跟随者,节点N+1,N+2,…,N+M表示领导者。智能体i的动力学模型描述如下:

(1)

本文针对事件触发通信下的高阶非线性多智能体,提出一种输出反馈包容控制方法,通过局部信息交互保证所有跟随者输出y1,y2,…,yN均收敛到由领导者输出yN+1,yN+2,…,yN+M所围成的动态凸包中,同时保证闭环系统所有信号SGUUB。

1.3 技术引理

以下技术引理将用于推导本文的主要结论。

引理 1[27]定义向量和矩阵如下:

P=diag{pi}=diag{1/qi}

式中:1=[1,…,1]T。由上述定义可知P=PTf0和Q=QTf0。

式中:μ=mini≠j‖μi-μj‖/2。根据文献[30]可知,RBFNNs能够在紧集Ωx⊂Rq内以任意精度逼近函数F(x),即F(x)=WTS(x)+(x),x∈Ωx,式中W∈Rp为最优权值向量,(x)∈R为逼近误差并满足条件|(x)|≤m,m为正数。

2 控制协议设计

2.1 跟踪误差动态构建

(2)

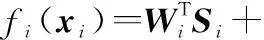
(3)

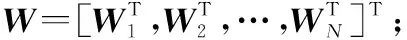
(4)

2.2 高增益观测器设计

本文采用如下的高增益观测器估计系统全状态信息[31]:

(5)

(6)

式中:Ψ=ηn+ρ1ηn-1+…+ρn-2η2+ρn-1η1。

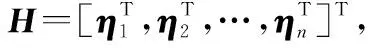
(7)

随后,计算H的i阶导数可得

(8)

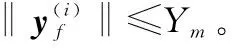
2.3 动态事件触发通信机制设计

(9)

(10)

式中:ћ,δ和γ为正的设计参数。

(11)

对上式左右两端分别进行积分可得

(12)

2.4 输出反馈包容控制设计

基于上述分析,设计如下的输出反馈包容控制协议:

(13)

(14)

式中:Γ=L⊗I;L=diag[Γ1,Γ2,…,ΓN];Γ=L⊗I为正的设计参数。

进一步,将式(13)代入式(3)可得

(15)

3 稳定性分析

3.1 群系统稳定性分析

本节首先分析动态事件触发通信下高阶非线性多智能体的稳定性结果,然后证明Zeno现象不存在。

定理 1考虑由动力学系统(1)所组成的多智能体网络,在输出反馈包容控制协议(13)、自适应更新律(14)以及动态事件触发通信机制(9)的作用下,闭环系统所有信号SGUUB,同时领导者和跟随者之间的包容误差收敛到原点附近的任意小邻域内。

证明首先构造Lyapunov函数如下:

(16)

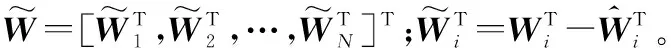
根据式(14)～式(16),求V关于时间的导数可得

(17)

由文献[29]的推论4.2和文献[2]的引理1可知,存在常数Wm,Sm,εm,ym使得‖W‖≤Wm,‖S‖≤Sm,‖‖≤m,成立。另一方面,根据式(8)下方结论可得+λ2X3+λ3X4)。将上述不等式代入式(17)可得

(18)

式中:

λmax(P)λmax(L1)(λmax(L-1)(ξm+2)ћ+

2WmSm+kξm+ym+m)-4δλmin(P)-

2λmax(A1)‖Λ‖+λmax(L1)Zm)

(λmax(A1)+λmax(L1))λmax(P)Smξm)

β=σ-(λmax(A1)+λmax(L1))λmax(P)Smξm-

Smλmax(P)λmax(A1)

结合式(16)可进一步改写不等式(18)为

(19)

式中:参数μ具有如下形式:

求解不等式(19)可得

V(t)≤(V(0)-ω/μ)e-μt+ω/μ

(20)

3.2 排除Zeno现象

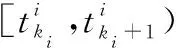
(21)

式中:

随后,将式(21)改写为

(22)

(23)

式中:ν和ι设置为

结合式(22)和式(23)可得

(24)

(25)

根据式(25)可进一步得到:

(26)

(27)

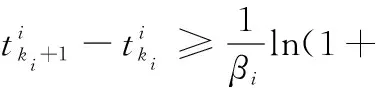
(28)

至此已得到事件触发间隔的下确界。

4 动态自触发通信机制设计

(29)

(30)

计算|eξi(t)|2的右上迪尼导数可得

(31)

为获得D+|eξi(t)|2的上界,由式(15)可得

(32)

(33)

结合式(30)和式(33)可得自触发间隔:

(34)

由此构建如下的动态自触发通信机制:

(35)

由式(34)可知

(36)

所提出的动态自触发通信机制(35)兼具了DETM[11-14]和自触发机制[15-23]的优势,一方面通过引入动态变量(29)获得更大的事件触发阈值,降低了网络信号采样频次;另一方面取消了连续监测系统状态信息这一限制性假设条件,仅需当前状态信息即可解算下一采样时刻,在保证群系统包容误差快速收敛的基础上动态调整网络信号采样频率,进一步节省网络通信资源与传感器资源。

5 仿真分析

本节以高超声速飞行器(hypersonic flight vehicle, HFV)群系统为例,验证所提出控制方法的有效性和理论分析的正确性。

5.1 模型陈述

考虑由4个领导者和4个跟随者组成的HFV群系统,其中第i架HFV的纵向动力学方程表示如下:

(37)

式中:hi,γi,αi,qi,xi,Vi分别为高度,航迹角,迎角,俯仰角速度,前向位移,速度;ηij,mi,Iiyy,gi,ζij,ωij分别为第j个广义弹性模态,飞行器质量,转动惯量,重力加速度,阻尼比,自然频率;Li,Di,Ti,Mi,Nij分别为升力,阻力,推力,俯仰力矩,广义弹性力,其表达式如下:

(38)

5.2 模型解耦

为方便模型分析,现有文献广泛采用一类面向控制的模型解耦方法,其将运动学模型(37)分为垂直动态[hi,γi,αi,qi]T和前向动态[xi,Vi]T。由文献[34]可知,在巡航段航迹角γi通常较小,为简化模型可采用近似值sinγi≈γi。此外,由于在巡航段迎角αi足够小,导致Tisinαi远小于Li,因此现有文献通常忽略Tisinαi对航迹角γi动态的影响[34]。综上,建立不确定垂直动态如下:

(39)

式中:

复合扰动

由结构弹性和外部干扰Δih,Δiγ,Δiα,Δiq(如阵风,湍流和大气扰动)生成。建立前向动态:

(40)

式中:

此外,复合扰动

式中:Δix,ΔiV为外部干扰。

5.3 模型转化

为方便控制设计,定义一组状态变量{xij},i∈N1:4,由此可将垂直动态(39)转化为如下Brunovsky标准型:

(41)

通过定义xi(t)=[xi1(t),xi2(t),…,xi4(t)]T∈R4,可将式(41)进一步转化为如下形式:

(42)

式(42)表明,垂直动态(39)已经转化为与式(1)相同的形式,因此可以直接应用所提出的控制方法。同时,对前向动态采用相同的系统转化方法。

5.4 仿真验证

考虑4个领导者和4个跟随者组成的HFV群系统,其中Laplacian矩阵设置如下:

设置作动器δie和Φi的幅值限制分别为δie∈[-20°,20°]和Φi∈[0.05,1.2]。同时,设置HFV群系统的初始位置如下:

h1(0)=85 830 ft,x1(0)=960 ft

h2(0)=85 480 ft,x2(0)=1 070 ft

h3(0)=84 660 ft,x3(0)=580 ft

h4(0)=84 130 ft,x4(0)=1 280 ft

h5(0)=86 000 ft,x5(0)=900 ft

h6(0)=85 700 ft,x6(0)=2 000 ft

h7(0)=85 200 ft,x7(0)=0 ft

h8(0)=83 800 ft,x8(0)=1 200 ft

在仿真实验中,设计参数对系统的收敛性能有着多重影响:设计较大的k,ћ和Γi会提升系统收敛速率,但同时也会增大包容误差的收敛范围。因此,需要在收敛速率和跟踪精度之间进行权衡。此外,选择较小的正常数σ能够减小自适应估计误差的收敛范围,但也会带来更加严重的抖振现象。由文献[31]可知,参数κ通常设置为一个小的正常数,且通过选择较小的设计参数ρ1,ρ2,ρ3,λ1,λ2和λ3,能够将包容误差的收敛范围调整至任意小。另一方面,设置较大的γ和较小的δ,可以减小包容误差的收敛范围,但同时也会增加信号采样频次。因此,在实际工程中,参数γ和δ的选取应在收敛性能和通信成本之间进行平衡调整。

仿真以0.01 s的固定步长运行300 s,所获得的结果如图1～图7所示。图1为HFV群系统的飞行轨迹和跟踪性能。

图1 HFV群系统的飞行轨迹和跟踪性能Fig.1 HFV swarms flight trajectories and tracking performance

图2 群系统编队队形变化过程Fig.2 Formation changing process of swarm system

HFV刚体状态的运行轨迹如图3所示,可见所提出的控制方法具有快速的收敛速度和光滑的瞬态性能,并且面对外部干扰展示出较强的鲁棒性。

图3 HFVs刚性状态Fig.3 Rigid-body states of HFVs

图4分别展示了所提出DETM以及动态自触发机制(dynamic self-triggered mechanism, DSTM)下的采样信号和控制输入。

图4 采样信号与控制输入Fig.4 Sampling signals and control inputs

图5分别给出了DETM和DSTM下的信号采样误差eξi(t),i∈N1:4。

图6 采样瞬间Fig.6 Sampling instants

为进一步说明所提出事件触发机制的优越性,将DETM,DSTM与现有SETM[35]进行对比,其触发条件为

为公平对比,对3种事件触发通信机制设置相同的参数。仿真结果如图7和表1所示。

表1 3种触发机制下的采样次数Table 1 Sampling times of three triggering mechanisms

图7 3种触发机制下的采样次数Fig.7 Sampling times of three triggering mechanism

相比于静态事件触发通信机制[35],所提出动态事件触发通信机制的信号采样次数更少,具有更高的通信资源利用率。另一方面,尽管动态自触发通信机制的信号采样次数更多,但具有无需连续监测系统状态信息的显著优势,更贴近于实际工程应用。

6 结 论

本文研究了动态自触发通信机制下,高阶非线性多智能体的输出反馈包容控制问题。首先综合考虑动态事件触发和自触发机制的优势,提出一种动态自触发通信机制,在具有更大触发阈值的同时无需连续监测系统状态信息,减少了信号采样频次和系统能量耗散;进而依据智能体邻接个体的相对信息为智能体设计输出反馈控制协议,驱使跟随者收敛到由多个领导者围成的动态凸包中,实现网络的多领导者包容控制;最后以HFV群系统为例验证了所提出方法的有效性。未来的研究方向包括时变拓扑、切换拓扑下动态自触发通信机制设计,以及所提出控制方法在实际HFV缩比模型上的仿真实验研究。