基于改进自抗扰控制的电动伺服系统机械谐振抑制方法

莫 昱, 唐旭东

(北京机械设备研究所, 北京 100854)

0 引 言

电动伺服系统是导弹稳定控制系统的执行系统,它通过接收控制系统的指令,驱动导弹舵面按照规定的角度偏转,或者改变导弹发动机的推力矢量,以保证导弹准确命中目标。随着稀土永磁电机及以数字信号处理(digital signal processing, DSP)为核心的控制器件性能指标的显著提升,当今世界各主要军事强国均加大了对电动伺服系统的技术研究及应用力度, 并取得显著成果[1-4]。

导弹在发射和高速自主飞行过程中,受到冲击作用,同时振动引起的惯性力、弹性回复力及附加空气动力作用于整个弹体,有可能会导致结构发生谐振。电动伺服系统一般由控制器、传动机构、电机以及反馈元件等组成,其中传动机构作为系统功率输出的主要环节,由于受到自身结构刚度的限制,在一定的频段会出现导致系统产生机械谐振的谐振频率。随着当前电动伺服系统的动态性能的进一步提高,系统带宽会覆盖传动系统的谐振频率,使得系统容易出现机械谐振的现象,严重危害系统的正常工作[5-6]。

国内外对于伺服系统的机械谐振也进行了深入的研究,一般采用优化机械设计和控制方法两种抑制方法,机械设计一般采用减震、隔振措施,增加系统复杂度,提高成本,当系统工作环境发生变化时,仍有可能再次出现谐振问题[7-8]。控制方法包括主动和被动两种抑制方式。被动方式主要采用带阻、低通滤波算法,需要首先进行谐振频率的辨识,这种方法往往对系统参数敏感,影响系统性能[9-11]。主动抑制主要通过自适应控制来消除谐振影响,包括基于状态观测的反馈控制、自整定和自适应控制等,能够有效抑制伺服系统中的机械谐振现象[12-14]。近年来出现的自抗扰控制(active disturbance rejection controller, ADRC)是一种基于系统模型扩展的鲁棒控制方法,通过扩张状态观测器(extended state observer, ESO)将系统的不确定性及扰动作为总扰动,并对其进行实时估计,再通过误差反馈进行补偿。ADRC可以有效地抑制外界干扰,提高系统抗干扰能力,同时通过非线性状态误差反馈(nonlinear state error feedback, NLSEF)实现控制系统“大误差,小增益;小误差,大增益”的控制品质[15-18]。传统ADRC算法复杂,并且采用非线性函数,调整参数多、计算量大。实际应用中可以用低阶的ADRC来控制高阶对象,并且当采用较小步长时,也可用线性函数来构成,仍能取得较好控制效果。

为了提高导弹电动伺服系统的可靠性和稳定性,本文从系统优化设计出发,引入改进ADRC算法,给出了具体的线性化算法。ADRC使得系统由临界稳定状态变为稳定状态,增加系统可靠性。针对ADRC算法参数的最优组合,提出一种基于混沌算法和摄动因子的改进粒子群优化(particle swarm optimization, PSO)算法,并将该算法应用于线性ADRC参数的整定优化中。最后通过试验验证了方法的可行性、有效性。

1 电动伺服系统

随着电动伺服设计向全数字化、集成化、智能化的方向发展[19]。本系统设计的电动伺服系统采用1台控制器+4路电机驱动电路的控制架构,通过4路驱动电路控制4台伺服电机,形成完整的电动伺服系统,如图1所示。

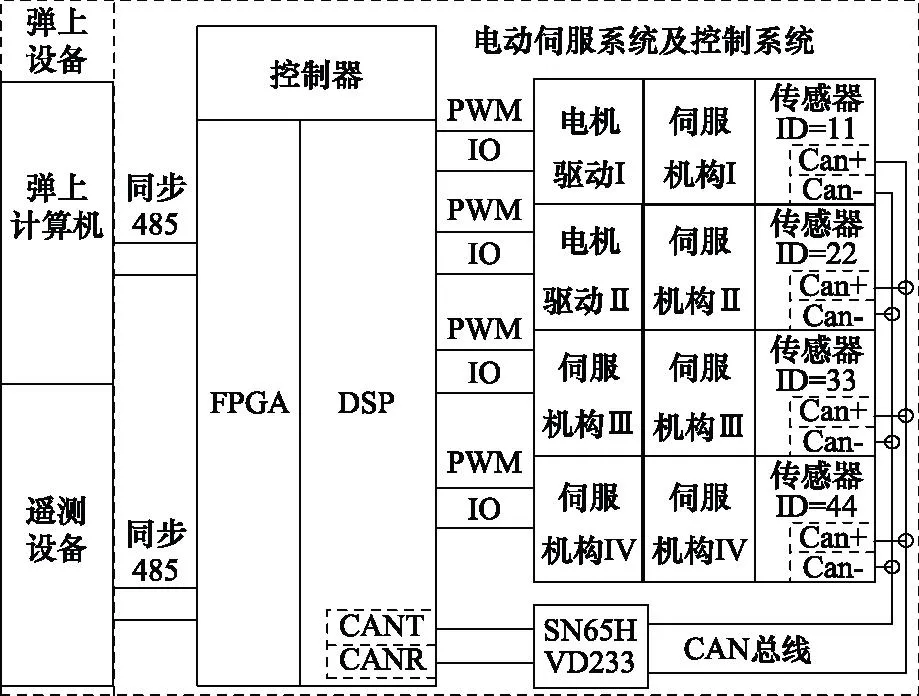
图1 电动伺服系统结构Fig.1 Structure of electric servo system

本文中电动伺服系统要求负载能力强、输出效率高,因此传动机构采用减速齿轮+滚珠丝杠+拨叉的结构形式。伺服电机为电动伺服系统的动力元件,通过适当的减速比设计,传动机构将电机的高转速转变为伺服系统输出轴的低速转动,实现减速增扭,驱动舵面偏转,反馈传感器与输出轴同轴安装,电动伺服系统传动原理图如图2和图3所示。电动伺服系统控制器采用DSP和现场编程门阵列(field-programmable gate array,FPGA)芯片架构,实现电机的脉冲宽度调制(pluse width modulaiton,PWM)控制以及相关信号数据的运算处理。电机驱动模块采用厚膜印刷工艺制造的数字式无刷直流电机驱动电路,具有体积小、稳定性高以及保护可靠等优点;反馈传感器采用符合CAN协议的非接触磁感应数字式角位移传感器;电动伺服系统控制器与导弹其他设备的通信采取同步485总线协议。

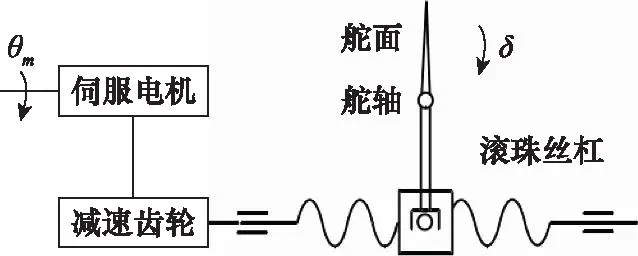
图2 电动伺服系统原理图Fig.2 Schematic diagram of electric servo system

图3 舵面装配示意图Fig.3 Schematic diagram of rudder surface assembly

2 电动伺服系统机械谐振机理分析

2.1 伺服系统数学模型

电动伺服系统可以简化成一个二惯量柔性连接的模型[20]。分别将伺服电机和负载作为研究对象分析,可以得到以下方程:

(1)

式中:JM为电机转动惯量;J1为负载转动惯量;DM为电机阻尼系数;D1为负载阻尼系数;Dω为传动轴阻尼系数;ωM为电机转速;ω1为负载转速;TM为电机电磁转矩;T1为负载转矩;Tω为轴距;K为传动轴弹性系数;积分上限x≥0。对式(1)进行拉普拉斯变换。由于本电动伺服系统采用电动机+减速齿轮+滚珠丝杠+拨叉的结构形式,传动效率较高,阻尼力矩与负载力矩相比,不到负载力矩的2%,在设计的初始阶段忽略阻尼系数,得到电机转速和负载转速与电机电磁转矩之间的传递函数和框图,如图4所示,表达式为

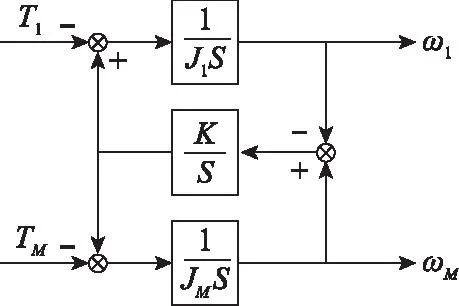
图4 传动机构简化框图Fig.4 Simplified diagram of transmission mechanism

(2)

2.2 谐振机理分析

将式(2)变换成下面的形式:

(3)

从式(3)可以看出,电动伺服系统模型中电机的转速与转矩的传递函数分为惯性环节、二阶振荡环节两部分。由于实际系统的传动部分非理想刚体,其刚度特性对系统的动态性能会产生直接影响,反映在系统模型中则表现为二阶振荡环节。在低频段系统传递函数可以将高阶部分省略,简化为1/(JM+J1)s,此时系统特性表现为惯量特性,不会出现由于系统刚度不足而产生的振荡现象;而当系统频率进入中高频段时,系统模型中的二阶振荡环节特性将逐渐体现。通过对系统传递函数特征根的分析,在s平面中会存在一对共轭零极点。当共轭零极点靠近虚轴时,系统的稳定性将会减小,这样系统在一定频率下将会出现明显的振荡现象,引起机械谐振。分别令式(3)中的分母和分子为零,可以得到共轭极点,即系统的自然振动频率fA:

(4)

共轭零点,即系统的抗谐振频率fN:

(5)

从式(4)可以看出谐振频率与刚度系数K和惯量J1、JM相关。定义惯量比R=J1/JM。

当电机转动惯量JM保持不变,惯量J1增加,惯量比增大,系统谐振频率变小。相对于刚度系数,由于系统惯量比的数量级较小,刚度系数对谐振频率的影响在量级上要远大于惯量比。

此外,传动间隙在很大程度上限制了电动伺服系统的性能,从动力学上看,间隙的出现,将导致同等受力条件下,结构位移和变形增加,即刚度降低。从传动环节分析,滚珠丝杠副的轴向间隙导致丝杠和螺母之间位移窜动,直接导致传动刚度和精度下降;齿轮、拨叉等传动部位,间隙将加剧磨损、产生速度振荡、降低系统传动刚度。在一定程度上,传动间隙会大大降低系统传动刚度,从而降低系统谐振频率,增大谐振幅值。

2.3 仿真分析

直流无刷电动机的二阶模型虽然未能反映无刷电动机特有的转矩脉动特性,但是在被控对象动态性能的主要特性上,二阶模型比较准确地反映了实际系统的特性,同时数学模型计算量得到大幅度降低。因此,本文建立电动伺服系统二阶数学仿真模型,引入间隙、阻尼等非线性参数,如图5所示。试验是在i5-2300 2.8 G,4 G内存的PC机上进行的。根据第2.3节建立的电动伺服系统数学模型,考虑电动伺服系统摩擦力、传动机构间隙、死区以及铰链力矩影响,其中模型参数如下:减速比Z=62,电机转动惯量Jd=1.7×10-4,舵面转动惯量Jz=0.025 3,传动机构效率η=0.896,电机转矩系数Kt=0.183,反电动势系数Ke=0.067,电机电枢电感La=0.4×10-3,电枢电阻Ra=0.3。

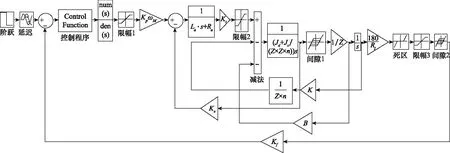
图5 电动伺服系统数学模型Fig.5 Mathematical model of electric servo system

调整模型非线性参数,将等效间隙值设置为0.06°,等效阻尼系数设置为-0.005,仿真结果显示电动伺服系统未发生谐振,如图6(a)所示。再次降低系统的刚度,将等效间隙值设置为0.16°,等效阻尼系数设置为-0.003,仿真结果显示电动伺服系统在稳态时产生频率为40 Hz,幅值为0.3°的谐振抖动,如图6(b)所示。

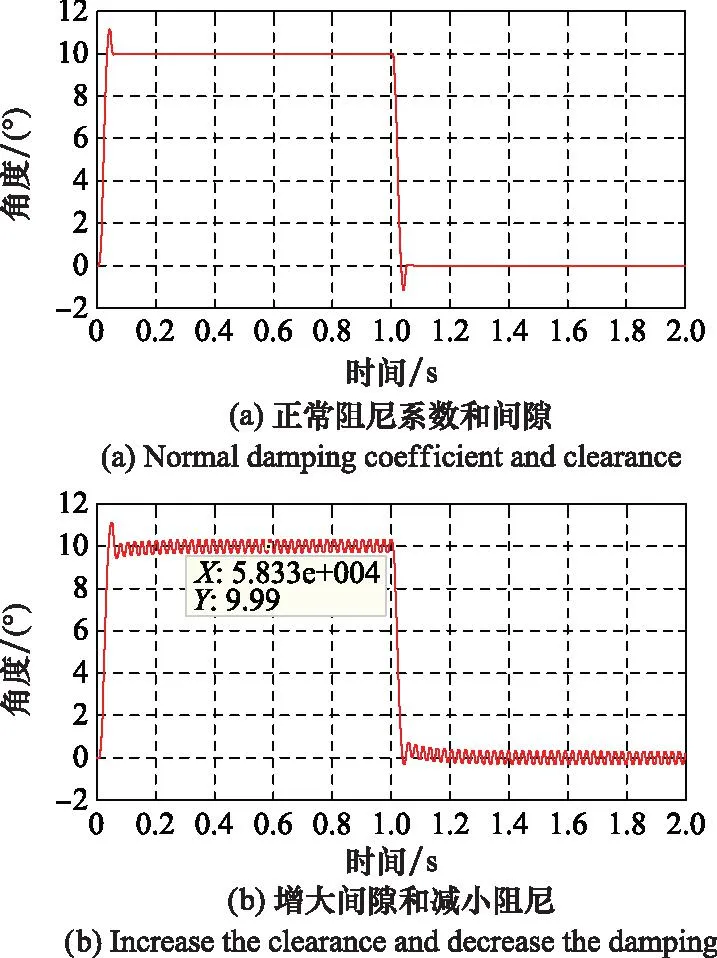
图6 10°阶跃仿真试验结果Fig.6 Results of 10° step simulation test

3 基于改进自抗扰的机械谐振抑制

谐振是机械系统的普遍问题,由于系统传动机构的刚度特性,电机输出的转矩和转速与系统负载端输出的力矩和转速并不相等,而是存在一定的差异。系统中的这部分特性可以通过在模型中引入一个二阶振荡环节来体现。二阶环节的阻尼比较小,当系统控制回路速度环增益增大时,系统稳定性下降,电机转速和电流将出现振荡现象,引起机械谐振。通过改善控制算法的途径抑制系统机械谐振,近年来在国内外自动控制领域得到了广泛关注,也取得许多研究成果。

3.1 线性ADRC算法

ADRC主要包含3个核心:跟踪微分器(tracking-differentiator, TD)、ESO、非线性组合。

基本ADRC的算法复杂,参数调节难度大,并且由于需要实时对扰动进行估计和补偿,对于系统硬件的计算能力和计算速度要求较高。因此,在保持ADRC控制精度高和鲁棒性好的前提下,应综合考虑其优势和局限性,根据实际需求选择适当的控制策略,提高系统综合性能。

韩京清研究员利用“等时区方法”确定出了二阶离散系统的最速控制综合函数fhan(·)。函数fhan(·)本身还有大量的非线性运算,直接运用,将大大增加运算量[14]。根据二阶系统,构造线性TD为如下结构:

(6)

安排合理的过渡过程就是调节参数kTD1和kTD2,使对输入的信号v0(t),能有一个期望的输出相对应信号v1(t)。kTD1和kTD2就是调节系统的极点,控制信号的跟踪速度。

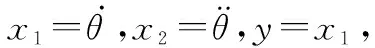
(7)

简化反馈控制器设计,采用线性反馈控制:

u=kp(v1-z1)+kd(v2-z2)

(8)

3.2 改进PSO算法

3.2.1 基本PSO算法

PSO算法将搜索空间设定为D维,粒子群总数为N,X=(x1,x2,…,xN),第i个粒子位置向量表示为xi=(xi1,xi2,…,xiD),速度向量表示为vi=(vi1,vi2,…,viD),粒子自身寻优的最优解,记为Pi=(pi1,pi2,…,piD),在整个群体中寻优的最优解,记为Pg=(pg1,pg2,…,pgD)。粒子每一次迭代运算后,对自己速度和位置[21-24]进行如下更新:

vij(t+1)=w·vij(t)+c1r1(pij-xij(t))+c2r2(pgi-xij(t))

(9)

(10)

xij(t+1)=xij(t)+vij(t+1)

(11)

(12)

式中:j=1,2,…,D;i=1,2,…,N;t为当前进化代数;r1和r2为[0,1]之间的随机数;c1和c2为学习因子;w为惯性权值。

基本PSO算法中每个粒子不仅受局部最优解Pi吸引,还受整个群体最优解Pg吸引。如果陷入局部最优,粒子也将快速收敛到相同的运动轨迹。因此,为了避免粒子早熟而停滞,要从加强粒子的动态搜索能力,具备跳出局部最优的措施等方面入手,提出改进PSO算法。

3.2.2 基于Logistic混沌序列的粒子初始化

混沌是在非线性系统中出现的行为复杂且类似随机,但是对初始值具有较强的敏感性,能够产生具有良好的相关性、随机性和复杂性的伪随机序列。因此,本文利用Logistic混沌序列这一典型的特点进行粒子位置的初始化,增加粒子种群的多样性、遍历性[25-27]。

Logistic混沌方程为

L(i+1)=μ·L(i)(1-L(i))

(13)

式中:控制参数μ∈[3.56,4.0],用来调整混沌状态的程度;L(i)∈(0,1)(i=1,2,…,D)。

对处于搜索空间为D维的m个粒子进行随机初始化,生成L1(1),L2(1),…,Lm(1)。将这m个初始值代入式(12)进行混沌方程运算,D次迭代运算后,产生m条混沌序列。从m条混沌序列中提取D个迭代值,代入下式:

i=1,2,…,D;k=1,2,…,m

(14)

即获得了粒子群中每个粒子的初始位置xki,表征第k个粒子的第i维坐标;通过式(13)计算得到所有粒子坐标xki组成的矩阵:

3.2.3 基于随机摄动的克服早熟停滞

粒子群在迭代运算过程中,如果出现Nmax次迭代运算,最优解不发生变化,即可判定算法陷入局部最优,出现早熟停滞。

定义早熟停滞计数器N,当最优解出现不更新时,计数器进行叠加,N=N+1,反之计数器清零。当N=Nmax时,则说明粒子群计算出现早熟停滞。此时,对粒子位置进行干预,引入随机摄动,使其跳出停滞状态:

xij=xij+λ(0.5-rand)

(15)

式中:λ为摄动因子; rand为[0,1]范围内的随机数。通过基于随机摄动的克服早熟停滞方法,可有效地避免出现陷入局部极优问题,提高粒子群的活跃度和遍历度,提升粒子寻优的能力。

3.2.4 算例分析

为了对比改进PSO算法与基本PSO算法全局搜索能力和快速性,选取两种典型的基准函数来进行测试,如表1所示。

表1 基准函数Table 1 Reference function

两种基准函数都是多峰值函数,最小值点都位于可行域的中间。选择基本PSO和本文的改进PSO算法,所有试验粒子群规模N=50,寻优代数t=1 000,基本PSO算法中,学习因子c1=c2=2.0, 惯性权值w=0.8, 改进PSO算法中,选取混沌控制参数μ=3.88,摄动因子λ=0.6。表2和表3列出了仿真实验结果。从表中结果可以看出:改进PSO与基本PSO算法相比,在收敛速度、寻优能力和最优值方面得到了显著提升,改进PSO算法都获得了最优解,克服早熟停滞,具有明显的优势。

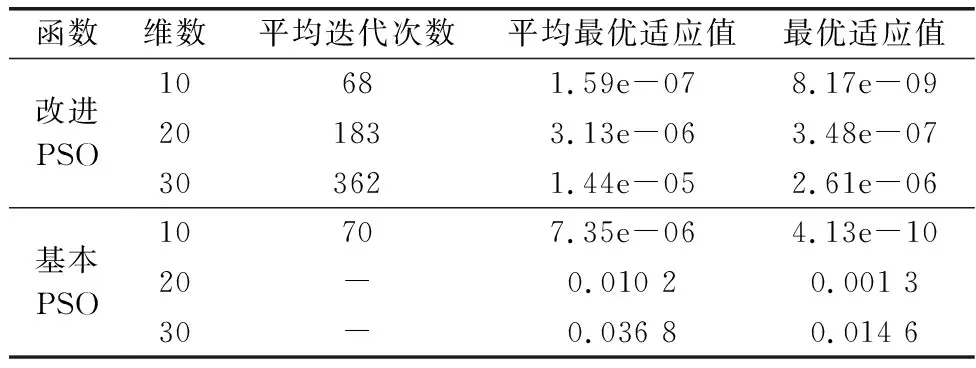
表2 Sphere函数结果Table 2 Results of Sphere function

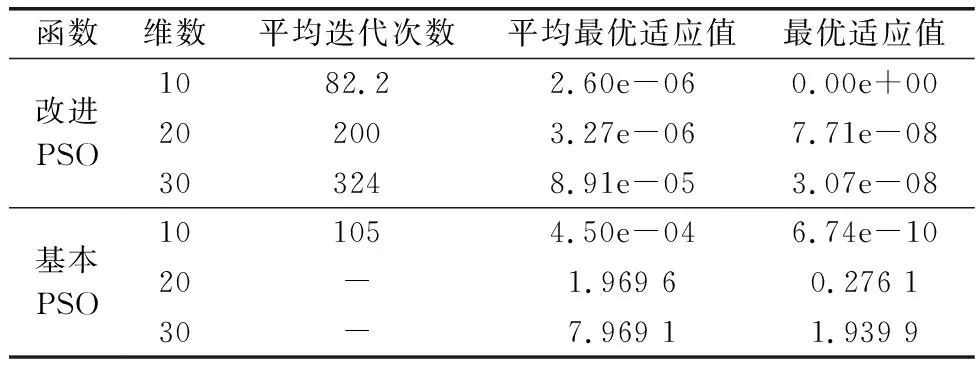
表3 Rastrigrin函数结果Table 3 Results of Rastrigrin function

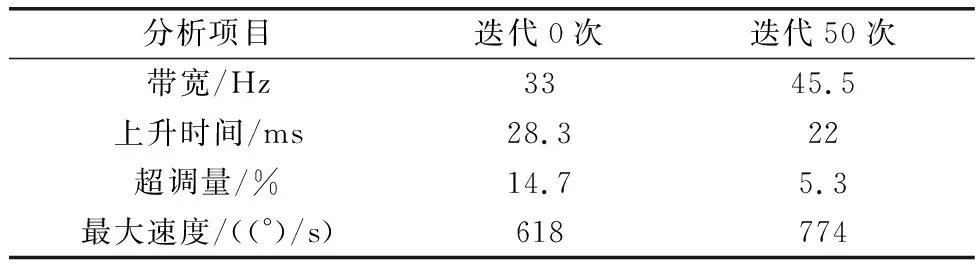
表4 结果分析Table 4 Result analysis

3.3 适应度函数的构建

线性ADRC模块中,需要优化的参数有β01,β02,β03,b,kp,kd,ki,kTD1,kTD2作为粒子群位置矢量在各维的分量,搜索空间维数设定为D=9。

每个粒子对应一个线性ADRC, 适应度函数用来评价该控制器的性能,采用控制系统最优设计中常用的

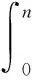
(16)

即误差绝对值积分,此指标越小表征系统性能越好。将此公式离散化,即

(17)

式中:T表示计算周期(取T=0.1 ms);ei为i时刻偏差值;n表示计算次数,将PSO的适应度函数设置为

F=J

(18)

标准的适应度函数只是表征了误差与时间性能指标的要求。在实际应用过程中,伺服系统不仅仅需要满足快速性,还要满足稳定性,尤其是超调量的要求。

对此,引入了惩戒因子β,粒子的目标函数变为

F=J+β·|e|

(19)

当伺服系统产生超调以后,惩戒因子β(β>0)将增加PSO的适应度值。

通过适应度函数的建立,就可以实现对ADRC控制参数准确评价,通过PSO算法寻找一组最优或接近最优的控制参数组合,使定义的适应度函数值最小,来改善伺服系统的动态响应特性、减少或消除静态误差。ADRC系统原理图如图7所示。

图7 ADRC系统结构图Fig.7 Structure diagram of ADRC system

3.4 改进PSO算法优化ADRC参数的流程

改进PSO算法优化ADRC参数的流程图如图8所示。

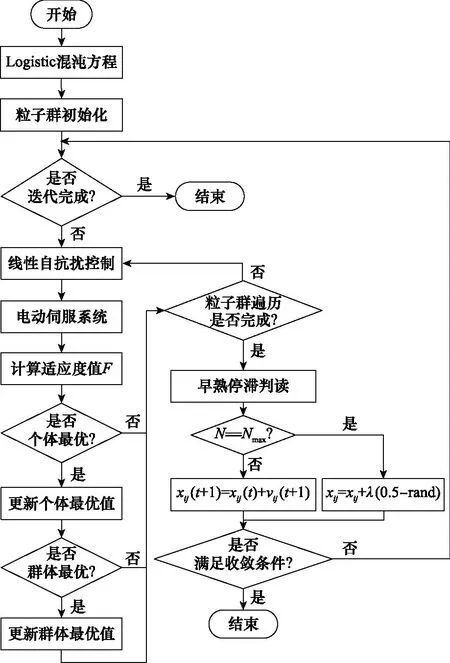
图8 流程图Fig.8 Flow chart

3.5 仿真试验

选用第2.3节模型,模型参数保持不变,改进PSO优化算法,维数D=9。PSO种群大小都取10,寻优代数为100,学习因子c1=c2=0.5, 惯性权值w=0.8,μ=3.88,摄动因子λ=0.6。 函数最佳适应度值进化结果如图9所示,改进PSO算法能够快速搜索到最优控制参数,同时通过判断粒子是否进入早熟停滞状态,采用摄动因子的作用,使粒子群遍历寻优。

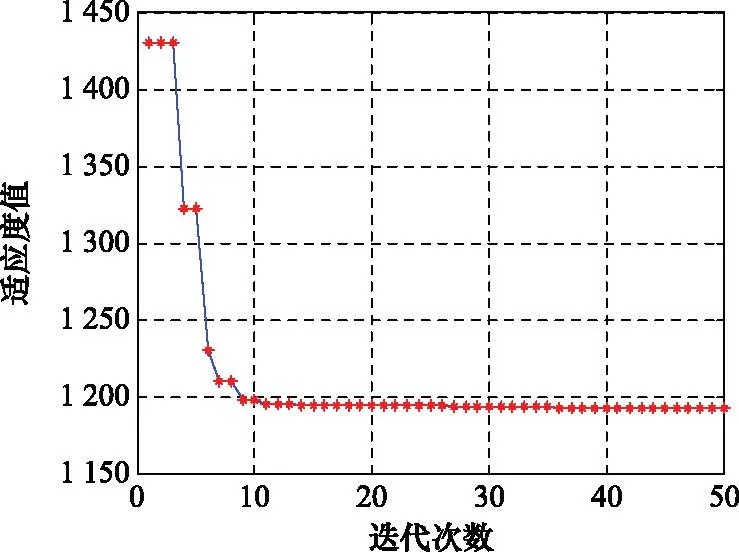
图9 适应度值进化曲线Fig.9 Evolution curve of optimal fitness value of function

试验中,舵偏角指令为10°,对比了进行50次迭代学习与第1次迭代学习控制结果。控制周期设置为0.1 ms,空载条件下(加舵面)舵系统对指令的响应曲线如图10所示。可以看到,经过改进PSO算法,参数寻优后,舵机系统振荡和超调明显改善,同时无稳态误差、舵机的快速性和运动速度提高。

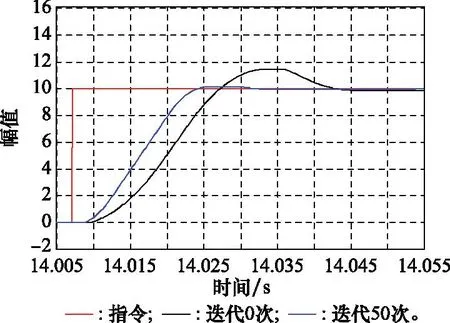
图10 时域对比测试结果Fig.10 Time domain comparison results

4 试验结果分析

电动伺服系统分别采用初始状态和采用改进ADRC算法进行对比试验。在没有采取改进措施的情况下,冲击试验后系统进行阶跃响应测试,此时系统稳定性明显下降,系统阶跃响应信号出现了周期性振荡现象,振荡幅值为±0.3°,频率为40 Hz,如图11所示。

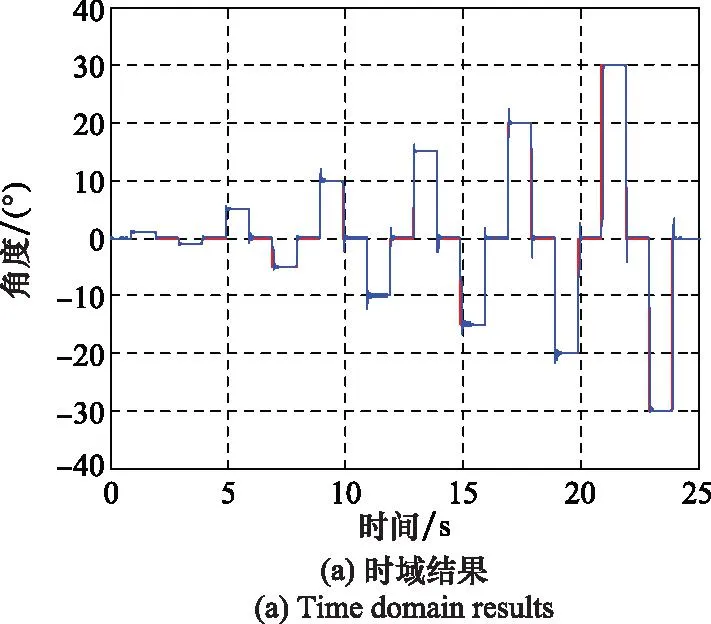
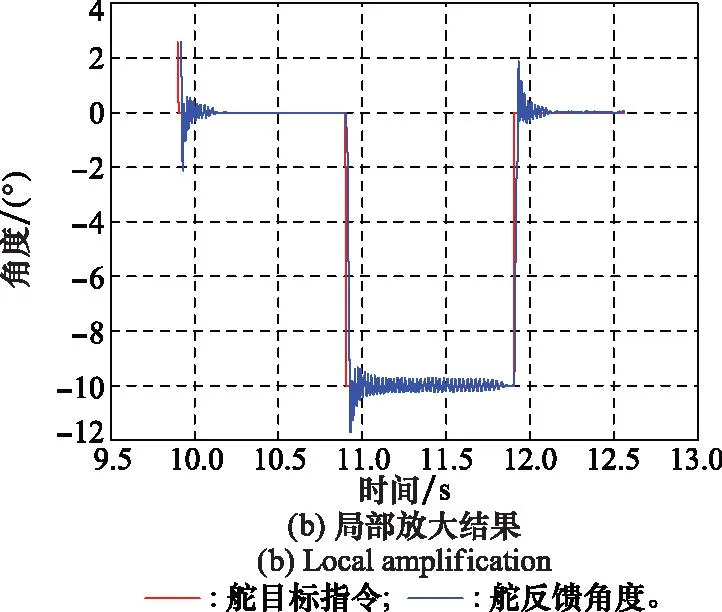
图11 改进措施前测试结果Fig.11 Results before improvement measures

采用改进ADRC算法后,四路伺服机构的控制周期为0.6 ms,每路控制周期控制在0.15 ms以内,与传统PID控制周期相当,电动伺服系统连续进行40、60次冲击测试,结果如图12和图13所示。从结果看,系统稳定性得到明显提高,周期性振荡现象消失,阶跃响应信号稳定收敛,证明ESO算法能够有效估计内部摄动、耦合以及外部干扰的总和并补偿。

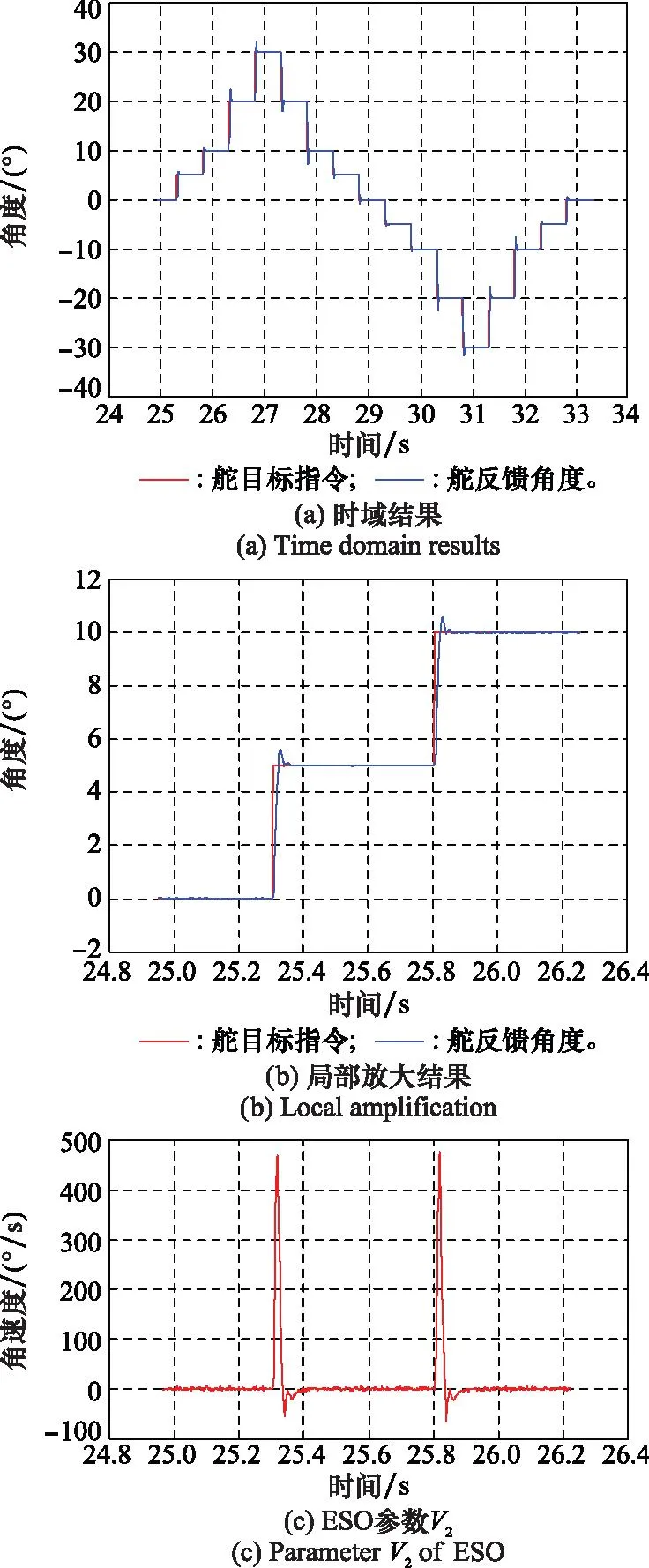
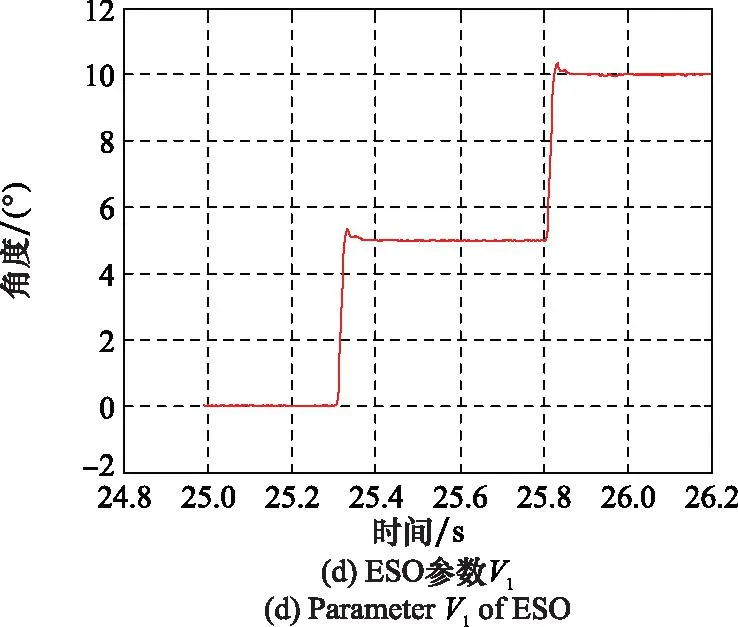
图12 改进措施后测试结果1Fig.12 Result 1 after improvement measures

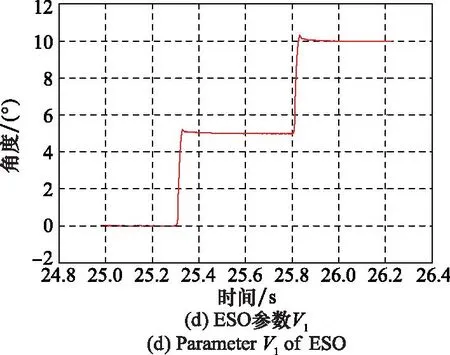
图13 改进措施后测试结果2Fig.13 Result 2 after improvement measures

为了模拟飞行过程中,环境振动对电动伺服系统的影响,采用振动激励方式进行验证:

(1) 正弦对数扫描振动,正弦对数扫描振动参数如表5所示;

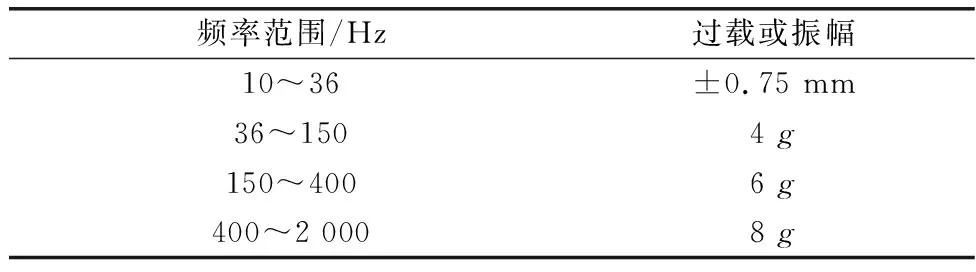
表5 正弦对数扫描振动参数Table 5 Parameters of sinusoidal logarithmic scanning vibration

(2) 扫描循环:10 Hz ～2 000 Hz～10 Hz,每一循环扫描时间5 min,循环次数2次;

(3) 振动方向:Y,Z两个轴向;

(4) 振动时间:每个轴向10 min;

(5) 在振动试验过程中,进行电动伺服系统测试。

测试结果如图14所示,从结果可以看出,在振动环境下,电动伺服系统能够稳定受控,没有出现机械谐振现象,结果稳定。

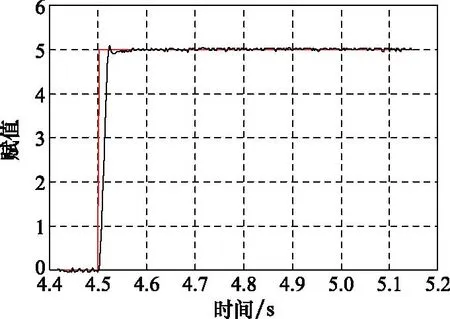
图14 振动环境下试验结果Fig.14 Result of vibration environment

5 结 论

为了满足现代军事作战对导弹机动性能的要求,高性能电动伺服系统逐渐成为弹上稳定控制系统执行系统的主流。为了提高电动伺服系统机械谐振抑制能力和性能,本文通过采用线性ADRC算法,并利用改进PSO算法的控制参数寻优方法,提高了电动伺服系统的动态和稳态性能,并通过仿真及实物试验验证了该方法的可行性、有效性。