空间目标远距离磁控方法及应用分析

赵宏亮, 张元文, 杨乐平, 黄 涣, 马 天

(国防科技大学空天科学学院, 湖南 长沙 410073)

0 引 言

随着航天技术的不断发展,电磁力/力矩作为一种新型航天器控制方式,具有非接触、高精度、连续、不消耗推进剂、无羽流污染等优势。因此,电磁力/力矩操控方式在航天器交会对接[1]、编队飞行[2]、在轨组装[3]以及失效航天器消旋[4]等方面受到广泛关注。但电磁力/力矩在操控空间目标的过程中存在两大局限性:一是电磁力/力矩的大小与作用距离的3到4次方成反比,导致电磁力/力矩的有效控制空间有限;二是电磁力/力矩和航天器间的相对运动均存在较强的非线性和耦合性,随着目标数量增加,非线性方程数量呈指数级增长,导致控制难度增加。针对上述问题,美国麻省理工大学提出利用由制冷机和超导线圈组成的电磁航天器编队,通过控制超导线圈中的电流,产生可控的强磁场,使得电磁航天器编队的控制能力可达到100 m[5]。其次,美国帕多瓦大学提出使用系绳航天器将电磁线圈通过系绳投送至电磁航天器附近产生电磁力/力矩可实现对目标航天器的电磁操控,但仍受到系绳固有长度的限制[6]。综上所述,现有的电磁力/力矩航天器相对运动操控方法,控制能力局限在100 m量级,仍然无法摆脱电磁效应的固有缺陷,对于相对运动速度较大,相对距离较远空间环境,电磁力/力矩的效能被大幅削弱的问题仍未完全得到解决。为解决上述问题,国防科技大学提出基于磁冻结等离子环磁场远距投送的方法,将强磁场冻结在等离子体中,并以高速发射,扩展磁场作用空间[7]。本文基于该磁场远距投送新型的磁控方法对其磁控能力及应用展开仿真分析。同轴枪等离子体加速可在高真空环境下产生高温、高速、高能量密度的等离子体射流[8-10]。目前,已经广泛应用于核聚变装置芯部加料[11-12]、等离子体空间推进[13-14]、天体物理现象模拟[15]。经过磁化同轴枪(同轴枪电极与通电线圈组成的一种强流脉冲放电装置,即磁冻结等离子体环生成装置)加速的等离子体环具有球马克约束位形,相较非磁化同轴枪加速得到的等离子体环而言,具有球马克位形的等离子体环的环向磁场和极向磁场均由等离子体电流产生,使得等离子体环结构更加稳定、寿命得以延长。美国菲利普斯实验室MARAUDER项目磁化同轴枪装置可以使得磁冻结等离子体环加速至200～1 000 km/s,且出口处的等离子体环的冻结磁场强度可达可0.1～0.5 T[16];日本的日本大学和九州大学可实现磁冻结等离子体环生成装置的高频率加注(约1 000 Hz)和点火(约10 Hz),其功率为3～5 MJ[17-18];中国科学院大学KTX-CTI装置可生成环形磁场强度为0.01 T速度为125 km/s的磁冻结等离子体环,并可以配合装置电路的多次放电实现等离子体环的高频次发射[19-20]。

本文根据磁化同轴枪产生的具有球马克位形的等离子体环并可将等离子体环及其所携带的冻结磁场进行高速远距投送的特点,提出一种新型的空间目标磁控方法,即通过将磁冻结等离子体环所携带的磁场投送至远处的空间目标附近,并与空间目标磁场相互作用,实现对空间目标的操控。此外,磁冻结等离子体环的寿命有限,与空间作用时间极短,一定程度上降低了等离子体环与空间目标间电磁力/力矩的强耦合性。该方法可有效拓展传统磁控空间,为突破现有电磁效应局限性提供新思路。本文在雪犁模型的基础上,结合分析力学方法,对磁冻结等离子体环的磁控能力展开分析、并对远距离电磁消旋任务、远距离伴星回收任务进行建模仿真与效能评估。

1 磁冻结等离子体环生成机理及其特征参数分析

1.1 磁冻结等离子体环生成机理

磁冻结等离子体环在高真空环境下(10-3Pa)由磁化同轴枪在强电流(106A)的作用生成[8-10]。其装置组成及场分布如图1所示,其中1为包含电容组的外部电路;2为产生偏置磁场的电磁线圈;3和4分别为同轴枪的内电极和外电极;5为线圈产生的稳态的偏置磁场;6为装置通电后内电极产生的环形磁场;7为被等离子体拉伸后的偏置磁场;8为等离子体环挣脱偏置磁场后磁重联形成的极向磁场;9为等离子体环冻结的环向磁场。等离子体环的生成过程如图1所示,首先电磁线圈通电在同轴枪内施加一稳态的偏置磁场,并向高真空的枪内快速加注一定质量的气体,如图1(a)所示;随后闭合外电路开关,在内外电极间的高压作用下被气体击穿,在两电极间形成高电导率的等离子体环并在洛伦兹力的作用下开始运动,如图1(b)所示;在等离子体环运动的过程中,由于环向磁场和通过等离子体的电流的相互作用产生的洛伦兹力,使携带冻结环向磁场的等离子体环轴向加速运动至管口,且在加速过程中受到偏置磁场产生的磁场张力,如图1(c)所示;最后,等离子体环附近的偏置磁场破裂重联构成极向磁场,此时形成具有球马克位形的等离子体环,如图1(d)所示。

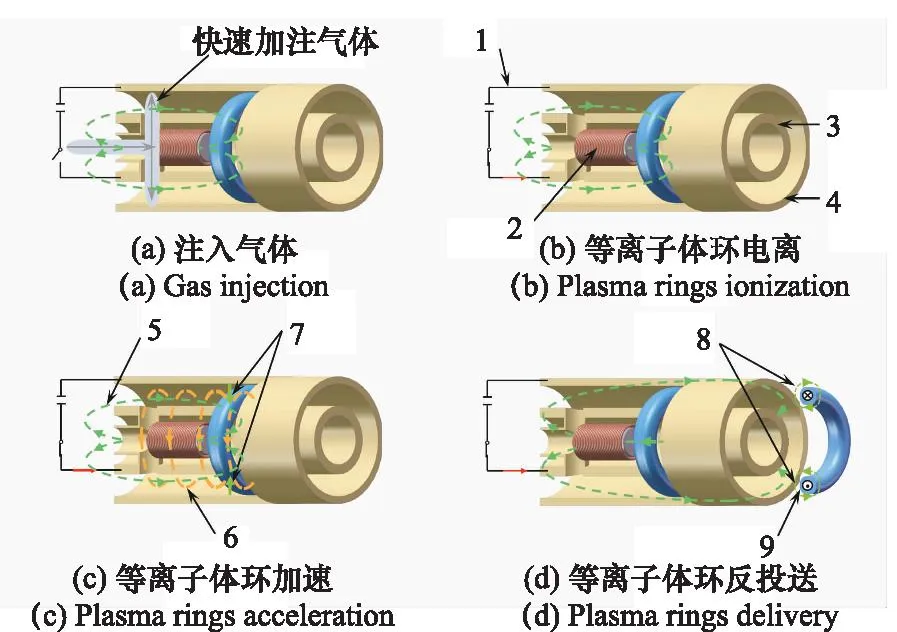
图1 磁化同轴枪结构及等离子体环的生成过程Fig.1 Structure of magnetized coaxial gun and formation process of plasma ring

1.2 雪犁模型及等离子体特征参数分析

磁冻结等离子体环的理论研究以雪犁模型为基础,随着磁流体理论的发展,磁冻结等离子体环的加速理论得以仿真验证[21-27]。北京航空航天大学通过实验验证了忽略偏置磁场张力的雪犁模型预测准确性,实验结果显示在误差所允许的范围内实验所测得磁冻结等离子体环的速度较雪犁模型预测速度较小[28]。中国科学技术大学研制紧凑环注入系统,并根据实验数据对装置的理论模型进行修正[19-20]。为了方便计算和对比仿真结果,本文所采用雪犁模型对等离子体环的特征参数进行预测计算,雪犁模型示意图如图2所示,雪犁模型等效电路图如图3所示。

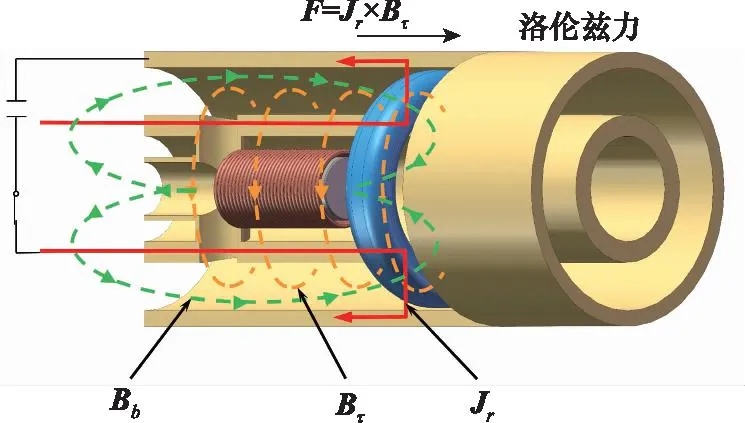
图2 雪犁模型Fig.2 Snow-plow model

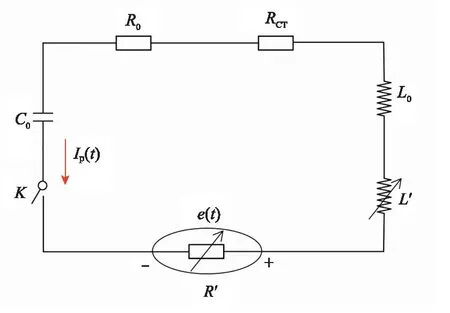
图3 雪犁模型等效电路Fig.3 Equivalent circuit of snow-plow model

雪犁模型在模拟等离子加速的研究中做了如下假设:

(1) 同轴枪内的气体,随着等离子体电流片的扫过全部电离,且电离后的离子随着电流片一起以相同的速度运动。

(2) 只考虑电流片与磁场的轴向作用,即洛伦兹力均匀分布在等离子体电流片上。简化了等离子体鞘层的空间分布。

因此,等离子体环的动力学方程可表示为

(1)

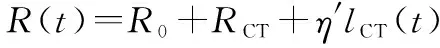
如式(1)所示,雪犁模型为二阶常微分方程组,为了探寻其特征参数的关系,现将雪犁模型改写成一阶方程组形式,令y1=Ip(t),y2=lCT(t),y3=dIp(t)/dt,y4=dlCT(t)/dt,则有雪犁模型的一阶方程组形式:

(2)

通过给定式(2)初始条件y1(0)=0,y2(0)=lCT(0),y3(0)=U0/L0+θlCT(0),y4(0)=0,可计算等离子体环的加速过程中的每个时刻放电电流、轴向速度、动能以及磁化同轴枪装置的加速效率等特征参数。现根据美国菲利普斯实验室MARAUDER项目磁化同轴枪装置[16,29](参数如表1所示),模拟得到1 mg、10 mg和50 mg的工质气体下的等离子体加速状态如图4所示。

表1 磁化同轴枪参数Table 1 Magnetized coaxial gun device parameters

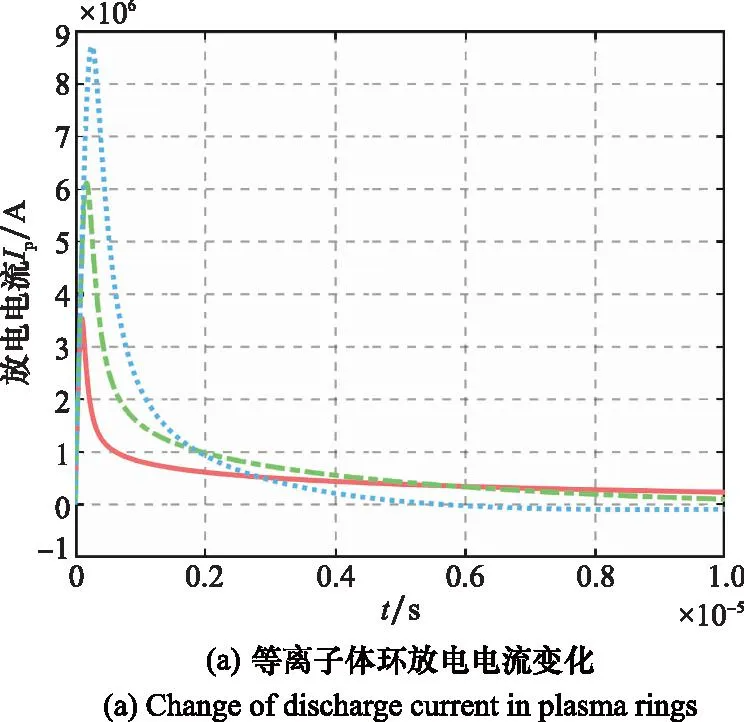
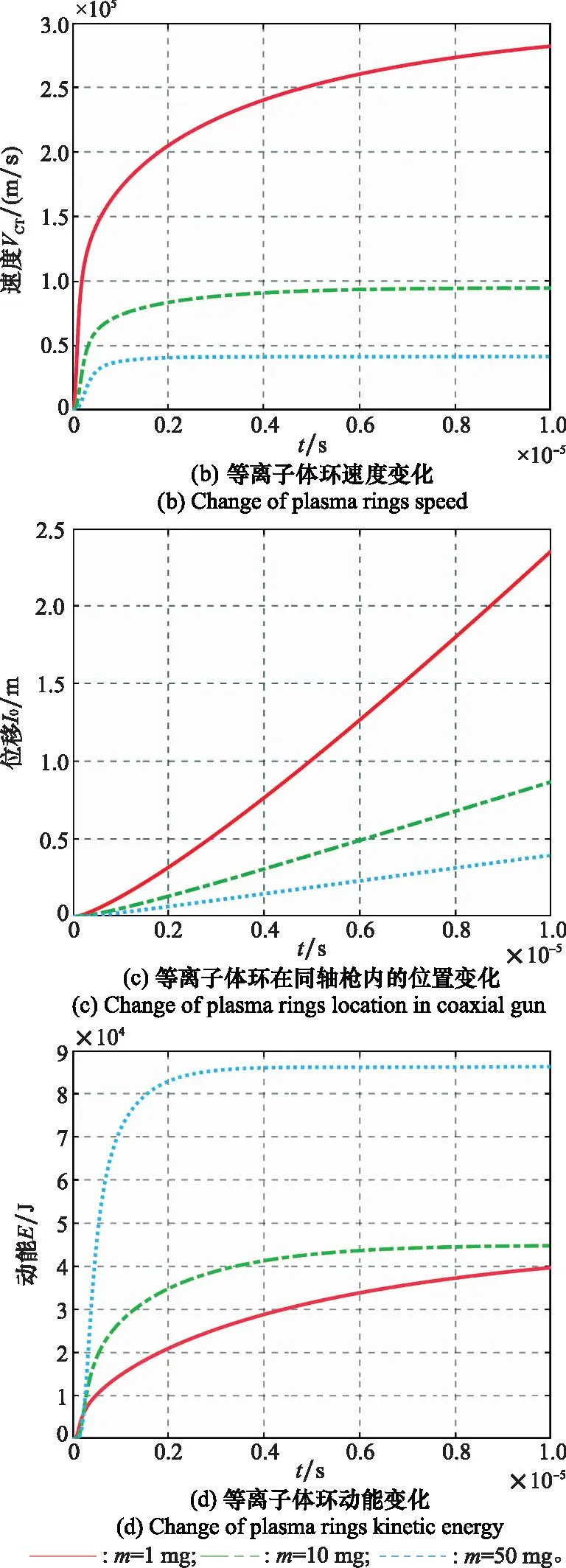
图4 基于雪犁模型仿真的等离子体环相关参数变化Fig.4 Changes of plasma ring related parameters based on snow-plow model simulation

2 磁冻结等离子体环的空间目标磁控能力分析

2.1 磁冻结等离子体环寿命

具有球马克约束位形的等离子体环经过同轴枪加速射出后进入自我维持的投送状态,在投送过程中无后续能量供给且存在阻性损失(占据主导地位)、等离子体重合及非闭合磁通损失等[30],导致其寿命有限,其寿命TCT公式为

(3)

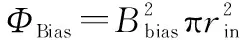
(4)

式中:I0为等离子体环出口位置的放电电流,且在等离子体环投送过程中等离子体构型保持不变且整体速度保持不变。在本文建模的动力系统模型中,将等离子体环假设为一具有高速的、小质量的、电流衰减的电磁线圈与空间目标相互作用,当磁冻结等离子体环运动至空间目标附近时,等离子体环受空间目标磁场影响被破坏,等离子体环与空间目标作用过程结束。

2.2 磁冻结等离子体环的磁控机理及其能力分析

如图4(b)所示,等离子体环的速度为105m/s,已经大幅超过第三宇宙速度,且等离子体环寿命有限,其有效作用空间在1 km量级内。根据CW方程,磁冻结等离子体环在空间中相对于同轴枪的运动可近似视为直线运动。则有运动过程如图5所示,磁化同轴枪装置向空间目标投送磁冻结等离子体环,在运动过程中等离子体环磁场与空间目标磁场相互作用,相互影响,当等离子体环运动到目标航天器附近时,等离子体环结构被航天器附近的强磁场撕裂破坏,而失去作用。

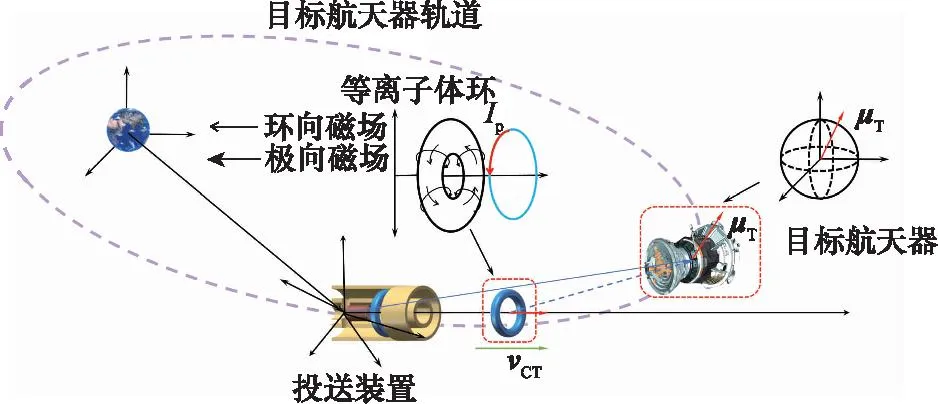
图5 磁冻结等离子体环磁控机理Fig.5 Magnetic control mechanism of magnetic frozen plasma ring

根据式(4)等离子体环在投送过程中放电电流呈线性衰减,则有等离子体环在运动过程中在s位置矢量处产生磁场为

(5)

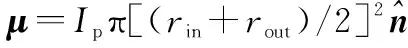
表2 等离子体环参数Table 2 Plasma rings state parameters

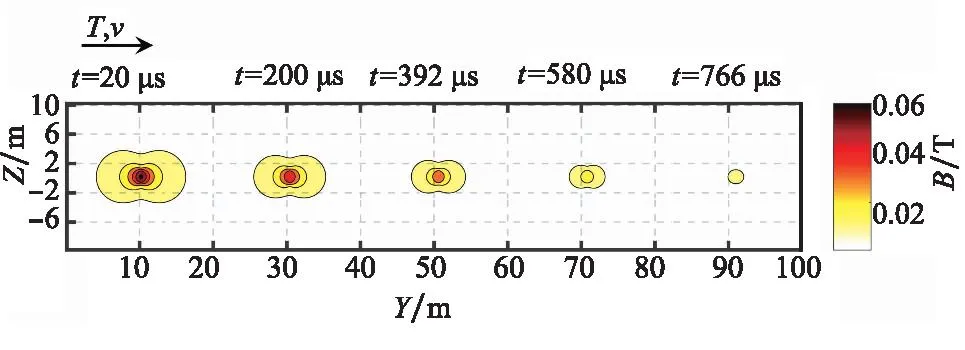
图6 磁冻结等离子体环磁势阱Fig.6 Magnetic potential well of magnetic frozen plasma ring

由图6可知,等离子体环在输运过程中磁场有效作用范围逐渐变小,等离子体环耗散或被航天器附近的强磁场破坏。在等离子体运动的轨迹中形成一个动态变化的磁势阱。磁势阱始终处于等离子体环运动中心,时间分布上,最大磁势阱始终位于磁冻结等离子体环的出口位置。

根据等离子体环的出口速度vCT及等离子体环寿命,可初步计算得到目标航天器在一个动态磁势阱周期下的脉冲速度冲量ΔvT:

(6)

式中:MT为空间目标质量;μCTi和μT分别为等离子体环和目标的磁矩矢量;r=APs0-vCTTCT为磁冻结等离子体环与空间目标的相对距离。

现在最大电磁力/力矩的情况下,等离子环投送状态如表3所示,对投送方向100 m处10 kg的目标航天器可获得的速度冲量进行仿真,空间目标在最大电磁力/力矩情况下获得的速度冲量如图7所示。

表3 等离子环投送状态Table 3 Plasma rings delivery state

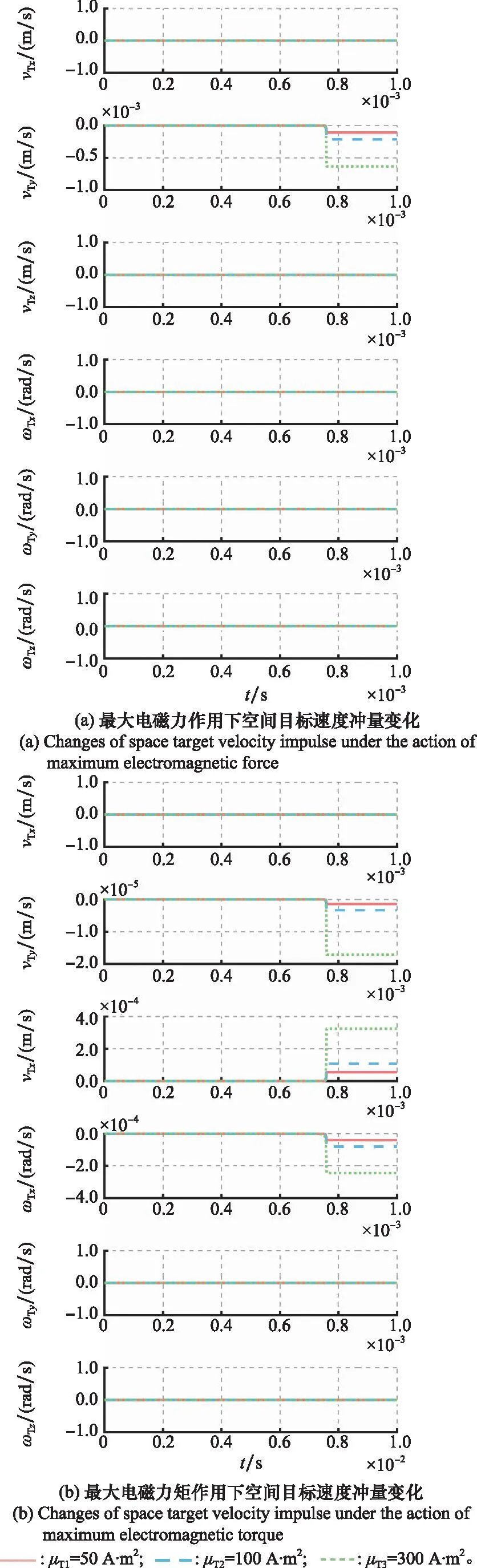
图7 基于雪犁模型仿真的等离子体环相关参数变化Fig.7 Corresponding parameters of plasma ring with snow plough model simulation

3 磁冻结等离子体环的空间目标磁控应用分析

基于磁冻结等离子体环投送过程中的磁场特性,本文提出等离子体环对空间目标的磁控方法,如图5所示操控航天器抵近空间目标,等离子体环射出方向由操控航天器指向空间目标,一是将等离子体环的磁场投送至旋转的失效航天器附近,失效航天器由于旋转产生的涡流磁场与操控航天器投送的等离子体环的磁场相互作用使得失效航天旋转速度降到回收阈值,便于后续失效航天器的拖曳离轨工作。此外,磁化同轴枪结构与等离子体推进器结构相似,可进一步与等离子推进器改装结合,更适用于未来太空碎片的清理等在轨任务。二是利用等离子体环的动态磁势阱对携带电磁装置的伴随卫星进行快速引导回收,等离子体环沿伴随卫星和操控航天器连线方向射出,携带电磁装置的伴随卫星沿等离子环磁势阱快速运动,实现伴星的快速相应回收。

本文基于上述任务背景分别开展地面场景下单自由度消旋仿真实验和快速响应伴星回收实验,并与传统电磁控制方法比对,针对其效能展开分析。

3.1 基于磁场远距投送的电磁消旋应用

3.1.1 电磁消旋模型

单自由度电磁消旋系统主要包括:电磁消旋装置与可控高精度高速旋转系统。

如图8所示,建立单自由度失效航天器电磁消旋模型[32-33]。

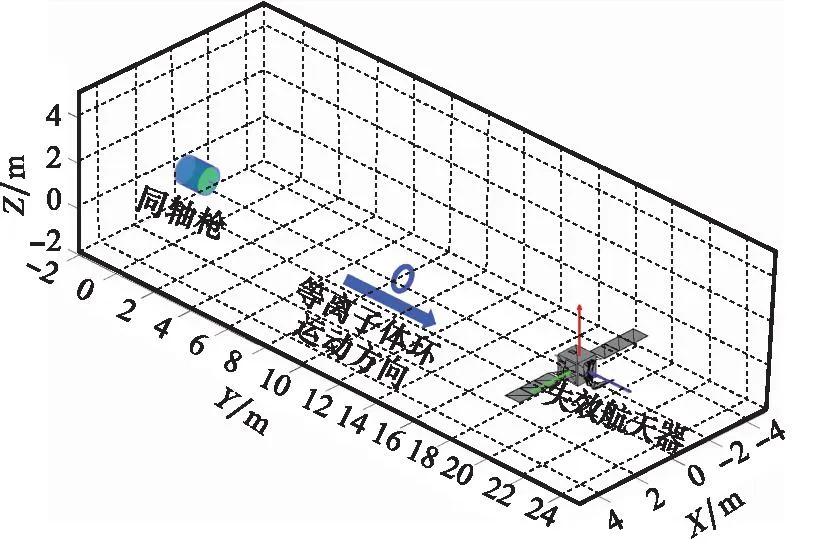
图8 单自由度电磁消旋系统Fig.8 Single-degree-of-freedom electromagnetic de-spin system

现假设失效航天器为一电导率为σ=35.335 69 s/m的铝制薄壁球壳,则有失效航天器在背景磁场B下的旋转动力学方程为

(7)

式中:ω为失效航天器绕旋转主轴的角速度;r1,r2分别为球壳的内径和外径;B⊥为垂直于旋转主轴磁场矢量;Mi为失效航天器质量;α为航天器角度矢量。将式(5)中等离子体环运动过程中的失效航天器位置处的强度B(s)代入式(7)中,即可求得失效航天器的角速度变化曲线。

3.1.2 数值仿真

磁化同轴枪参数如表1所示,等离子体环状态如表2所示,开展对50 m处的失效航天器消旋仿真。图9为等离子体环运动过程中在失效航天器附近产生的磁场强度,等离子体环在失效航天器附近5 m范围内,等离子体环的磁能效率得到大幅提升;如图10所示,在以8 Hz投送频率下和等离子体环的作用下,可在400 s以内完成对10 rad/s转速的失效航天器的消旋任务。

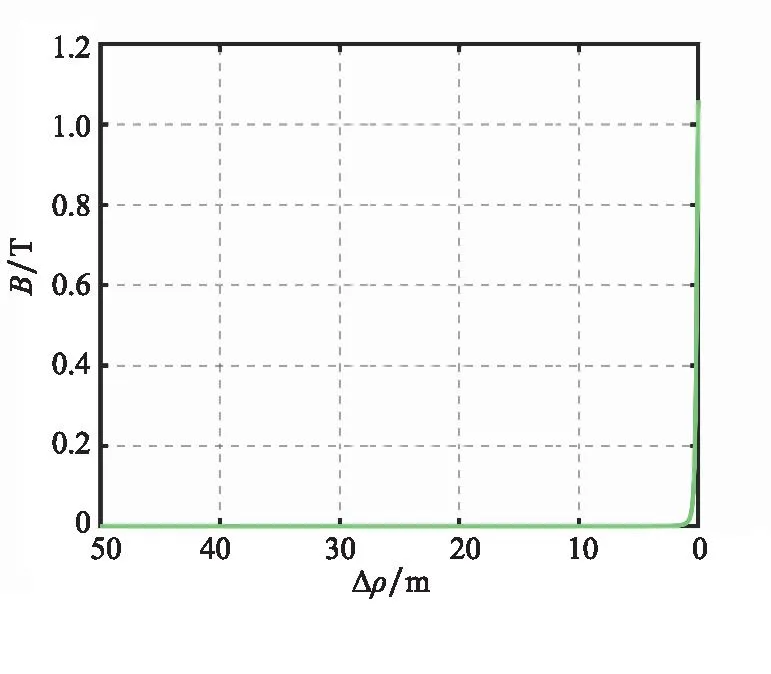
图9 目标航天器处磁场变化Fig.9 Magnetic field changes of target spacecraft

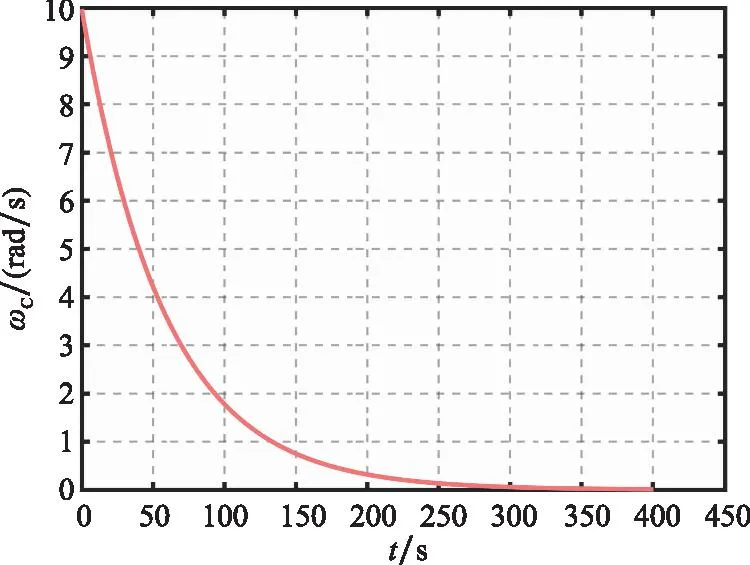
图10 目标航天器旋转速度变化Fig.10 Rotation speed changes of target spacecraft

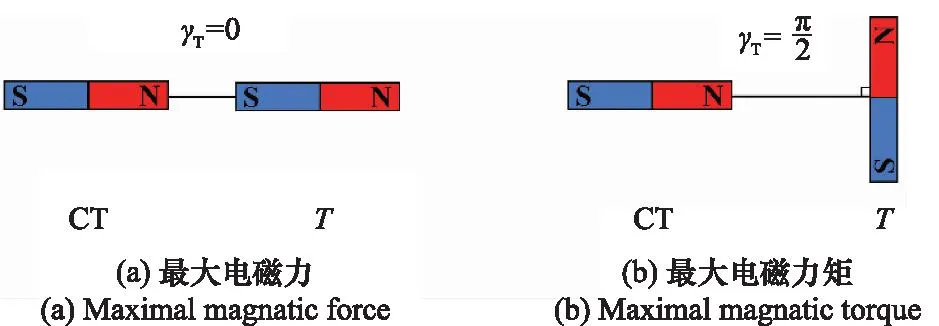
图11 伴星回收仿真场景Fig.11 Companion craft recovery simulation scene

基于上述仿真结果,在未考虑失效航天器产生的二级涡流场的情况下,可实现快速响应消旋,且磁能利用率大幅提高,便于失效航天器的快速回收,大幅缩短任务时间,扩大有效磁控空间,大幅提升操控航天器的安全性,延长了操控航天器的工作寿命。

本文所提出的基于磁冻结等离子体环远距投送的新型磁控方法,在电磁消旋任务中,磁冻结等离子体环可在失效航天器附近产生周期性动态磁场,在考虑由周期性变化磁场激发得到的二级或三级涡流场的情况下,可实现失效航天器的快速响应消旋,为失效航天器的快速离轨提供充分的准备工作。此外,对于非磁性材料的航天器或太空碎片而言,等离子体环在其附近产生的周期性磁场,可激发其二级涡流场,在等离子体环的磁场与二级涡流场的作用下可以使得非磁材料起旋,进一步利用涡流场实现对非磁性材料的航天器或太空碎片的电磁操控。

3.2 基于动态磁势阱引导的伴星回收应用

3.2.1 伴星回收模拟仿真分析

如图6所示,为验证伴星在磁冻结等离子体环动态磁势阱中的运动趋势,建立地面六自由度姿轨耦合地面仿真场景,初始回收状态如图8所示,分别为最大电磁力(见图6(a))和最大电磁力矩(见图6(b))两种状态。

在此基础上,建立伴星的相对运动模型,现假设同轴枪体坐标系与地球惯性坐标系重合记为OxEyEzE,等离子体环投送方向由同轴枪质心指向伴随卫星质心,伴随卫星T0和等离子体环CTi的体坐标系为Oxbiybizbi,(i=0,1,…,n),且分别由地球惯性坐标系进行3-2-1旋转得到,旋转角为αi,βi,γi(i=0,1,…,n)。设伴随位置卫星的位置矢量为xT,角度矢量为θT,角速度矢量为ωT,则有相对运动方程为

(8)

式中:μT为伴随卫星磁矩矢量;μCTi(i=1,2,…,n),为磁冻结等离子体环磁矩矢量;ρi=xCTi-xT(i=1,2,…,n)为等离子环与伴随卫星的位置矢量差,由等离子体环指向伴随卫星,其中ρi=‖ρi‖;C为3-2-1转系下的角速度转换矩阵;MT和JT分别为伴随卫星的质量和主轴转动惯量。

在以投送频率为f的序列等离子体环的作用下,μCTi、ρi具有周期特性。因此,在距离足够远的情况下,伴随卫星的运动状态也具有周期特性。

3.2.2 数值仿真

磁化同轴枪参数如表1所示,等离子体环状态如表2所示,开展对100 m处质量为10 kg的动态磁势阱引导伴随卫星回收的仿真验证,仿真结果如图12所示。

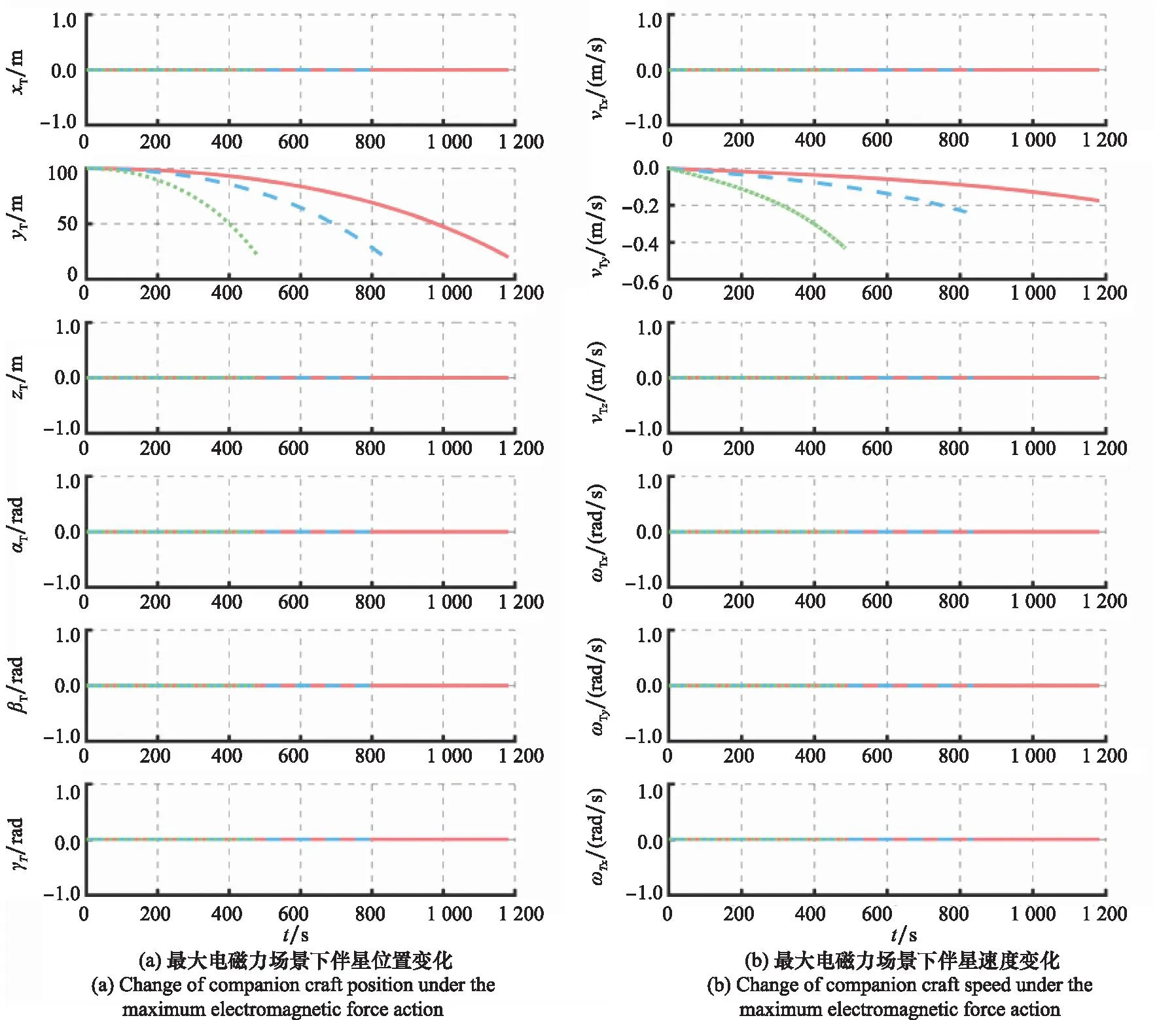
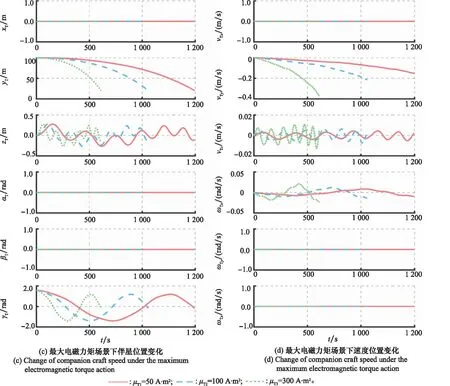
图12 伴星回收任务中伴星运动状态变化Fig.12 Changes of companion craft motion during the companion recovery mission

在磁冻结等离子体环动态磁势阱引导伴随卫星快速响应回收任务中,磁冻结等离子体环的动态磁势阱占据绝对主导地位,但在伴星回收的法向会因角度偏差引起可控的周期性小扰动,后续可结合传统电磁装置的电磁力混合控制实现对伴随卫星的精准回收,为伴星回收提供一种新型的、自适应的、快速响应的方法。此外,可通过磁冻结等离子体环动态磁势阱引导伴星回收过程可逆,进而可以引导伴随卫星进行精准投送任务。

4 结束语

磁场远距投送可有效拓展传统磁控空间及提升操控性能,为一亟待解决的科学与工程应用问题。

基于磁冻结等离子体环的特点,本文对其投送过程的放电状态、磁场变化、磁势阱等特征参量展开分析;在雪犁模型基础上,结合空间环境及在轨应用需求,提出一种可扩大磁控空间,提高磁能利用率,增加操控航天器安全性的新型磁控方法;基此建立了等离子体环远距投送的单自由度电磁消旋模型及六自由度伴星回收模型并展开仿真分析。仿真结果表明,随着同轴枪电容组电路和装置参数的改进,可有效提升等离子体环远距投送的磁控效能及磁控空间。目前,相关样机设计和实验验证工作已相继展开,后续可结合实验结果完善模型。

综上所述,本文所提基于磁冻结等离子体环磁场远距投送的新型磁控方法,为突破现有电磁效应局限性提供新思路,一是将冻结磁场强度可观的等离子体环以超高速度定向投送,有效扩展了磁控空间,提高磁能利用率,且一定程度上降低了磁场源间的强耦合性;二是可利用序列等离子体环产生的动态磁势阱,对电磁目标进行引导,在保持传统电磁操控的自适应性的同时,对可控自适应空间进行延伸;三是针对非磁性材料的涡流控制,磁控方法可利用其在目标处产生的动态变化磁场形成激发涡流场、控制等。