多状态系统任务成功性仿真评估
2024-01-16邵松世刘海涛袁昊劼张志华
邵松世, 刘海涛, 袁昊劼,*, 张志华
(1. 海军工程大学舰船与海洋学院, 湖北 武汉 430033; 2. 海军工程大学基础部, 湖北 武汉 430033)
0 引 言
任务成功性是描述装备/系统性能的一项重要指标,主要反映装备/系统在开始时处于可用状态的情况下,在规定的任务剖面中完成规定功能的能力[1-5],常用任务成功概率(mission success probability, MSP)来度量。任务成功性不仅与装备/系统的可靠性指标(如任务可靠度等)密切相关,还受到维修性、保障性等诸多因素的影响[6-9],可以综合地反映装备/系统完成规定任务的能力,因此受到人们的广泛关注。
任务成功性评估是指在装备/系统开始执行任务之前,评价和估计装备/系统成功完成任务的概率。当前,任务成功性评估主要可分为解析法和仿真法两大类[10-14]。
解析法通过分析任务单元的结构关系、保障资源与维修能力等,建立任务成功性的数学表达式并实现评估,主要有马尔可夫法、布尔扩展模型法等。如文献[15]通过构建多个并发执行的马尔可夫链描述航天器发射工程的状态转移关系,建立了航天器发射任务可靠度模型。文献[16]利用马尔可夫过程分析部件系统的状态转移过程,建立了复杂系统使用任务完成概率模型。文献[17]基于离散马尔可夫过程建立了多状态系统的任务成功性模型。文献[18-19]研究了备用冗余任务系统的优化模型。文献[20]利用相位建模方法研究了多状态系统动态评估方法。尽管马尔可夫模型在任务过程描述上比较清晰[21-22],但其数学解析相对复杂,特别是对于大型复杂系统,解算工作难以进行。文献[23]采用二元决策图方法建立了存在共因失效时的多阶段任务可靠度评估模型。文献[24]研究了多状态可修系统的任务成功度的重要度量方法,其所采用的布尔扩展模型法利用多态故障树、多值决策图等工具,将传统可靠性模型中的“二元”状态拓展为状态性能的多值刻画,但其对系统各状态之间的时变转移关注不足,难以解决复杂使用规则下的多状态系统的任务成功性建模问题。文献[25]在给出单台装备、多台相同装备任务成功概率(mission success probability, MSP)求解方法的基础上,利用系统的逻辑关系得到了复杂系统的MSP。文献[26]通过分析不同条件下单阶段MSP和多阶段复杂任务的逻辑关系,建立了多MSP模型。文献[27-28]建立了基于解析法的可修系统多阶段任务可靠度评估模型。文献[29]建立更新的冲击过程模型研究了MSP与系统生存概率之间的权衡关系。
仿真法则主要利用计算机仿真技术,根据装备的故障和维修规律,通过模拟系统、单元的工作状态和过程来评估任务成功性,主要有Petri网仿真法、蒙特卡罗仿真法、Metric模型仿真法、多智能体仿真法等。如文献[30]基于面向对象的Petri 网建立了可修系统常见故障的可靠性仿真模型。文献[31]建立了基于方差的分阶段任务系统可靠性分析模型。文献[32]建立了任务成功性判断模型,运用多智能体的方法和思路对航渡过程和设备故障进行了仿真。文献[33]研究了随机条件下多阶段MSP仿真评估方法,建立了存在随机共因失效条件下,不可中断和可中断随机多阶段任务的MSP评估流程,并结合算例进行了验证。文献[34]从阶段任务、装备战损和修复的角度,提出了考虑装备保障资源约束条件下的多阶段任务成功性仿真评估方法。
综合现有研究可以发现,解析法可以在相应的假设条件下较为准确地评估任务成功性,但在有些情形下,任务系统的使用约束和维修约束比较复杂,难以对其进行准确的解析描述。仿真法则大多假设单元只有正常和故障两种状态,而许多实际中的任务系统是多状态系统。假设某系统由n个单元组成,每个单元包含m个状态,则使用仿真法评估任务成功性时,需要处理的变量将达到mn个,当n和m较大时,仿真算法的复杂度会急剧增加。对于这类多单元多状态且使用约束和维修约束复杂的系统,鲜有文献研究其任务成功性评估方法,已有的各类方法也难以较好地解决该问题。针对这种情况,本文首先对系统进行原理分析,然后利用半马尔可夫过程,建立系统运行的状态转移模型,再通过分析使用、维修、资源等约束条件进行仿真设计,进而评估多状态系统的任务成功性,并结合示例分析方法的可行性。
1 问题描述
设某系统由n个单元共同组成,分别记为A1,A2,…,An,其中单元Ai(1≤i≤n)的状态Si有mi种,分别记为Si1,Si2,…,Simi,则对应的系统状态Ssys可用单元状态构成的有序数组表示,即
Ssys=(S1,S2,…,Sn)
为了更好地建立任务成功性模型,假设该系统满足如下要求:
(1) 单元与单元之间、单元运行工况之间相互独立,其分布参数可通过历史运行数据估计得到;
(2) 单元发生故障后实施换件修理,且修复如新,考虑执行海上任务,备件数量有限;
(3) 任务系统的状态由其组成单元的状态决定,当单元状态发生改变时,任务系统的运行状态将根据使用规则发生转移。
例如,某系统由3个单元A1、A2和B共同组成,其中A1、A2为相同的可修单元,B为不可修单元(定期检修)。系统的使用规则为:A1和A2互为备份,需经启动过程后进入工作状态,启动时间为t0,且启动状态不会发生故障;当且仅当A1和A2无法同时工作时启动单元B,B为热备,由其完成替代功能。一旦A1或A2能够正常启动进入工作状态后,则单元B停止工作并回到备用状态。系统的初始状态为A1启动、A2和B处于备用状态;当A1和A2同时无法工作且B处于故障状态时,系统任务失败。由此可见,A1、A2和B共3个单元的可能状态分别有4个、4个和3个。为了减少仿真变量,在考察系统运行规则的基础上,将其分为成功态和失败态两类,如表1所示。系统各状态的转移关系如图1所示。
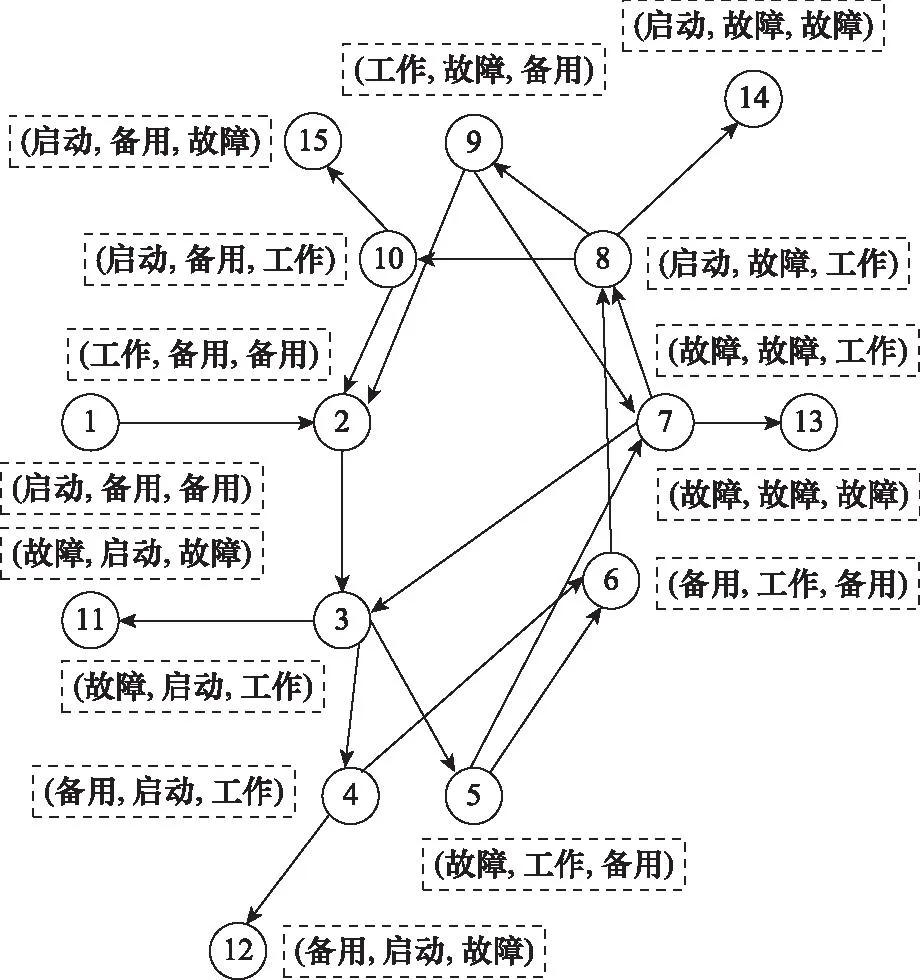
图1 系统状态转移示意图Fig.1 Schematic diagram of system state transition

表1 系统的实际运行状态示意图Table 1 Schematic diagram of the actual operating status of the system
2 系统状态转移模型
在得到系统状态转移关系的基础上,本节进一步描述状态持续时间分布及状态转移概率。
2.1 状态持续时间分布
系统在某个运行状态下的持续时间由其组成单元的寿命和维修时间共同决定。
设系统的当前运行状态,即系统启动后的第k个状态为
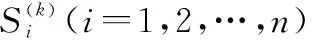
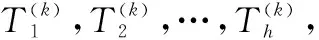
(1)
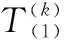
(2)
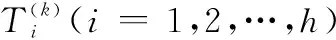
(3)
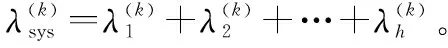
此时,系统的运行过程可以用马尔可夫过程描述。但考虑到许多系统在实际运行过程中还会受到使用、维修以及保障资源等约束,因此实际中的系统持续时间并不服从指数分布,此时系统运行过程服从半马尔可夫过程。
2.2 状态转移概率
系统的状态转移路径由使用规则决定,因此系统的状态转移概率实际上是“单元状态改变导致任务系统状态改变”这个事件的概率。
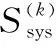
(4)
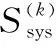
例如,对于第1节给出的由3个单元A1、A2和B组成的系统,其状态7(故障,故障,工作)的转移只有3种路径,分别为转移到状态3、8、13。其任务系统的状态转移概率P7,3、P7,8、P7,13分别为
P7,3=P(State7→State3)=
P7,8=P(State7→State8)=
P7,13=P(State7→State13)=
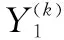
以此类推,可以得到该系统的状态转移概率矩阵Pt,其中Ptij表示系统由状态i转移到状态j的概率。
3 使用、维修与保障资源约束的作用机理
在系统的实际运行过程中,使用规则、维修时间和保障资源等方面的约束也会影响系统的任务成功性。为此,本节分析上述约束对系统任务成功性的作用机理。
3.1 使用规则约束
系统使用约束主要反映在使用规则之中。
(1) 单元状态最大持续时间。有些系统会对部分单元在特定状态下的最大持续时间进行限制。如一个由主单元和备用单元组成的冗余任务系统,当主单元出现故障时,则由备用单元承担相应功能。但由于备用单元的功能精度差于主单元,因此通常规定备用单元的最大持续运行时间。当主单元无法及时修复,进而导致备用单元超过规定的最大持续运行时间时,视为系统任务失败。
当部分单元有最大持续时间的规定时,这些约束将影响系统的状态转移进程。设单元Ai在状态Sij下的最大持续运行时间为Tij,max,则其在该状态下的实际持续时间为
(5)
(2) 单元状态最小持续时间。有些系统会对部分单元在特定状态下的最小持续时间进行限制,只有单元在该状态下的持续时间超过最小时间限制后,单元才有可能转移到其他状态。如单元最小启动时间,要求单元在启动状态的持续时间不低于规定时间。类似地,当单元Ai在状态Sij下的最小持续时间为Tij,min时,则其在该状态下的实际持续时间为
(6)
3.2 维修约束
常见的系统维修约束如下。
(1) 单元最大允许维修时间约束。在某些系统中,特定单元发生故障后需要在规定时间内将其修复,否则会造成任务失败,称这种约束为单元最大允许维修时间约束。
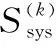
(2) 单元定期检修约束。对于任务系统中的重要单元,采用定期检修的维修方式,可将故障防范于未然。通过定期检修后,单元性能恢复如初,降低了故障发生率,提高了任务系统的成功性。
3.3 保障资源约束
在许多舰船装备/系统的实际运行过程中,特别是在执行航行任务时,保障资源对任务成功性的影响主要反映在携行备件的数量上。因此,本文主要考虑备件数量对任务成功性的影响。当某单元发生故障时,采取换件修理的方式进行维修。当某单元累计故障数大于备件数量时,则该单元无法维修,从而限制了系统的可行状态,导致状态转移概率发生变化,降低了任务成功性。
4 任务成功性仿真设计
4.1 约束条件的仿真表示
在无使用与维修约束的情况下,系统的状态转移可由第2.2节描述,任务系统的状态持续时间实际上是所有单元当前工况持续时间的最小值,而其任务系统的转移方向则由最早改变状态的单元来决定。若存在使用限制,组成任务系统的单元在该系统状态下的持续时间还应满足使用约束条件。因此,使用约束条件可以利用单元的寿命、维修时间或使用流程等表示。
例如,对第1节所描述的由3个单元A1、A2和B共同组成的系统,当单元B有单次最大持续工作时间TC,max,单元A1和A2的启动时间不低于t0时,该系统的使用约束可表示为
Use_restrn={min(TAs,TBs)≥t0,TC≤TC,max}
(7)
式中:TAs,TBs,TC分别表示单元A1和A2的启动时间和单元B的单次工作时间。当Use_restrn=1时,表明满足系统使用约束条件;反之,当Use_restrn=0时,表明不满足系统使用约束条件,即此次任务失败。
相对而言,维修约束与保障资源约束不仅涉及因素多,而且约束形式多样,需要针对不同任务系统特点确定维修约束Rep_restrn与保障资源约束Rse_restrn的表示方法。
对于保障资源约束,以备件等效为对单元进行的整体备件为例,假设任务系统由n个单元组成,第i个单元的备件数量为ni(i=1,2,…,n),则备件资源约束可表示为
(8)
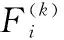
4.2 系统状态转移条件及仿真设计
(9)
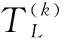
为方便表示任务系统的状态转移,设系统状态集合{Ssys}中共有N个元素,这些状态分别记为Se1,Se2,…,SeN。根据系统的工作流程,逐一判断系统能否从状态Sei一步转移到状态Sej,并用qij来表示。
(10)
特别地,qii=0(1≤i≤N)。
这样就构建了系统状态转移矩阵Q=(qij)N×N。状态转移矩阵Q的元素由0~1组成,反映系统状态的可能转移。显然,若系统状态Sei为成功态,则系统可从该状态转移到其他状态,即qij(1≤j≤N)不全为0;否则该系统状态为吸收态,即qij=0(1≤j≤N)。
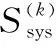
x(k+1)=Qx(k)
(11)
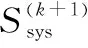
4.3 任务结束判断及任务成功率
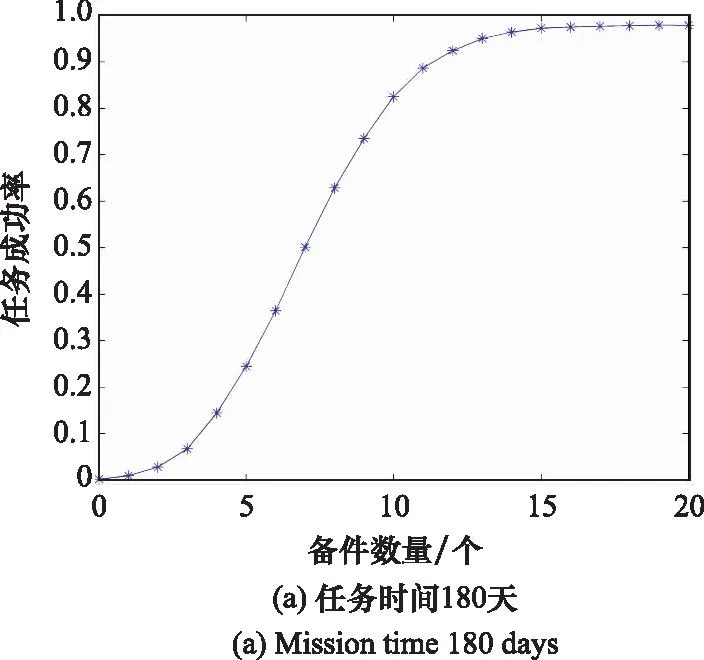
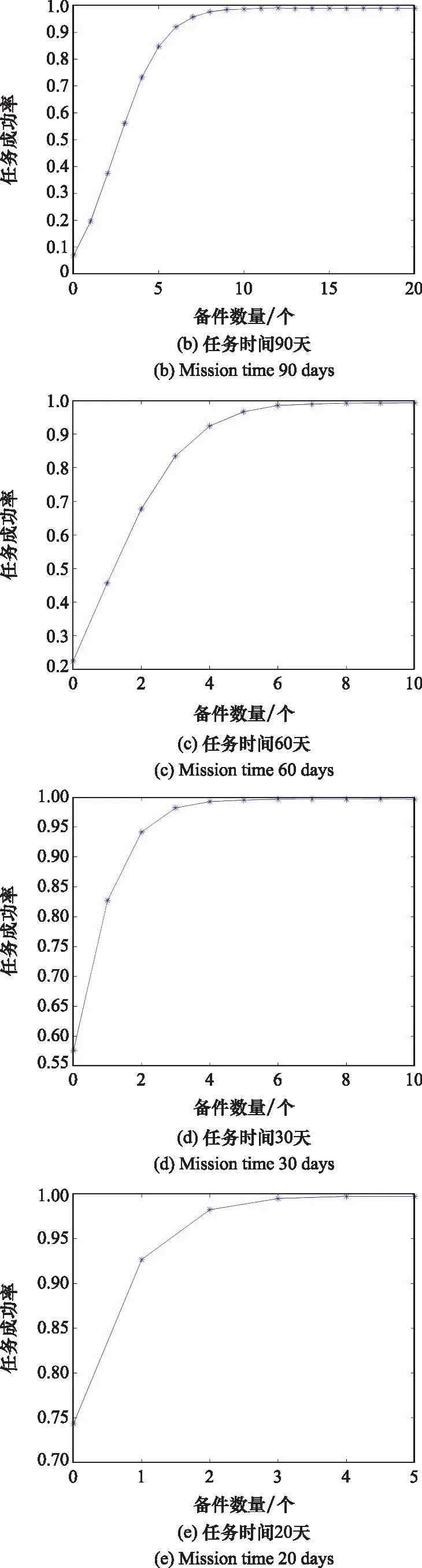
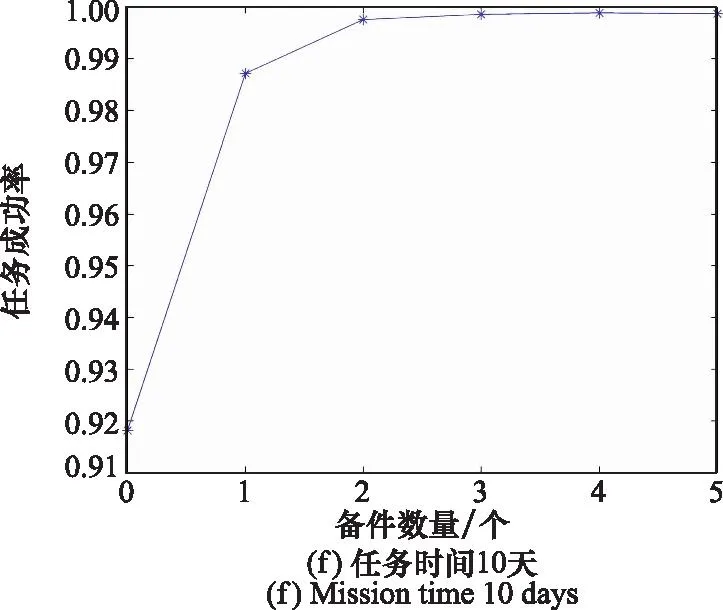
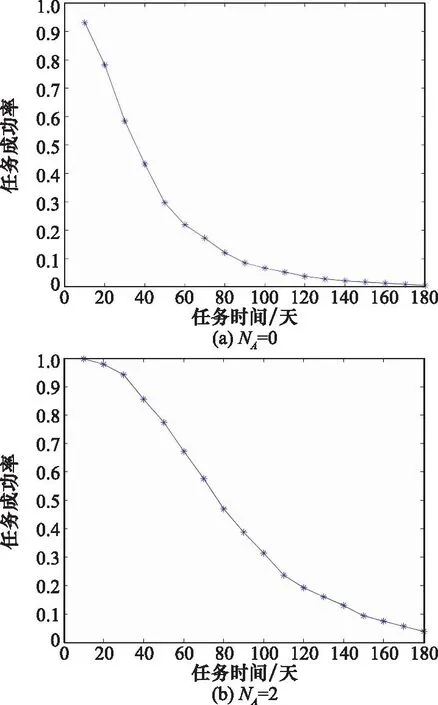
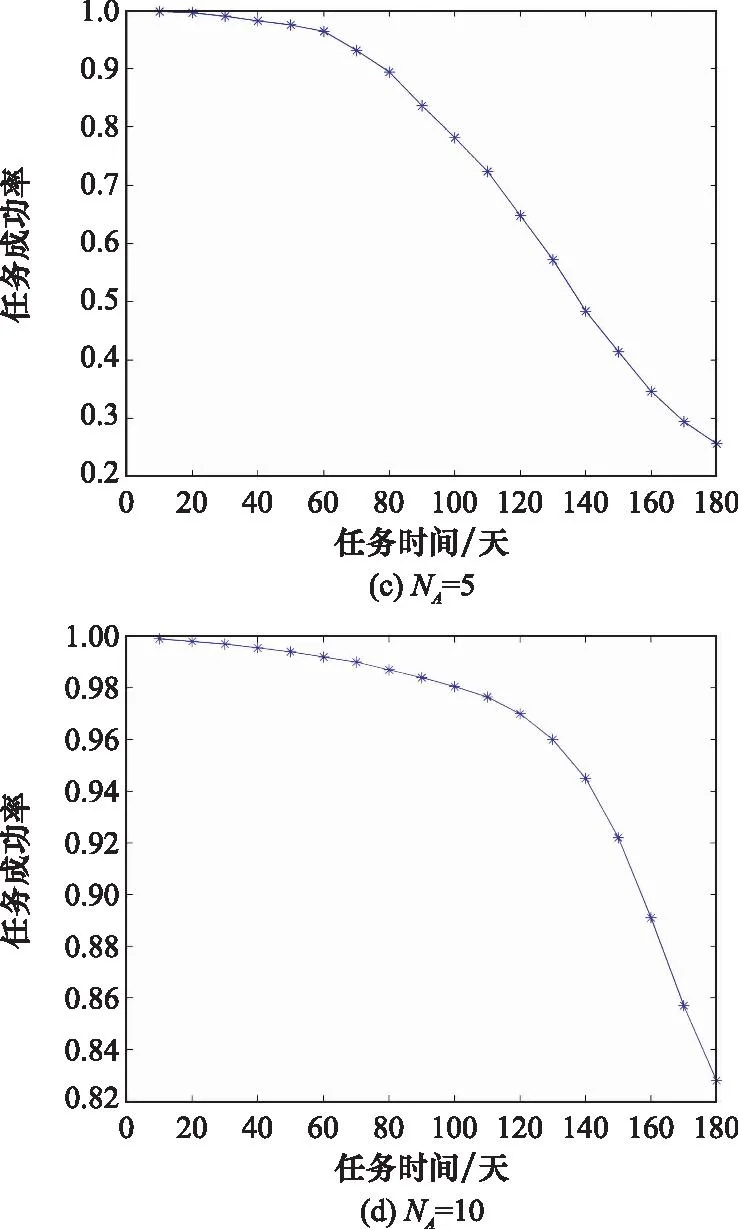
设任务时间为Tall,系统已运行时间为T。若T 由于仿真过程中涉及随机数的生成,因此单次任务结果也具有随机性。当对仿真过程重复R次时,记录任务成功的次数Rs,则Rs/R为仿真得到的任务成功的频率。根据大数定律可知,当仿真次数R无限增大时,任务成功的频率Rs/R依概率收敛到任务成功率。因此,仿真次数R足够大时,就可以用Rs/R近似表示任务成功率。通常可取仿真次数R在10 000到200 000之间。任务成功性仿真流程如图2所示。 图2 任务成功性仿真流程图Fig.2 Mission success simulation flowchart 某系统由3个单元A1、A2和B共同组成,其中A1和A2为相同的可修单元,B为不可修单元,系统的使用规则见第1节。根据该系统的实际背景,单元A1和A2的启动时间均为TAs=TBs=2 h,故障率λAB=1/500,维修率μAB=1;单元B故障率λC=1/800,单次最大工作时间TC,max=5 h;任务时间Tall=180天。 首先,根据使用规则,当A1和A2均不处于工作状态时,须由单元B代替工作,但由于单元B的误差会随工作时间的增加而逐渐加大,因此不能长时间单独承担任务,这就对单元B的单次连续工作时间提出了要求。其次,从维修角度看,由于单元B需在单元A1和A2同时发生故障时承担任务,期间一旦发生故障则系统任务失败,因此为了提高系统任务成功性,可考虑对单元B采用定期检修的方式提高其可用性。 经仿真发现:当设定单元B单次最大持续工作时间TC,max由5 h增加至10 h,系统任务成功率从97.53%提升至97.64%;当设定单元B的定期检修周期TC,re由2 h增加至10 h,系统任务成功率从97.70%降低至97.68%。这说明,在其他条件不变的情况下,单元B单次最大持续工作时间和定期检修对系统任务成功性的影响并不明显。这反映出在实际任务中,单元B通常是作为单元A1和A2均不在工作状态时的应急手段,在单元B自身可靠性较高的情况下,改变其使用约束与维修约束对任务系统成功性影响很小。这与装备执掌人员的经验是一致的,同时也为后续的系统设计或升级改造提供了理论支持。 由于系统在海上执行任务时只能携带有限数量的备件,因此当单元故障次数超过携行的备件数量时,单元会出现故障后无法维修的情形,进而可能影响系统的任务成功性。 设携带的单元A1和A2的备件数量为NA,任务时间为Tall天。首先观察在给定任务时间的条件下,任务成功率随整机备件数量的变化情况。根据该系统仿真模型,Tall分别取10、20、30、60、90、180天,各仿真200 000次,得到该系统的任务成功率随单元A1和A2备件数量变化趋势如图3所示。 图3 备件数量对系统任务成功率的影响Fig.3 Impact of spare parts quantity on the success rate of system mission 从图3可以看到,随着单元A1和A2备件数量的增加,系统任务成功率先快速提高,反映出备件对任务成功性有重要影响。但当备件数量增加到一定程度后,对任务成功率的提升十分缓慢,反映出备件存在保障效益溢出限制的现象。以任务时间为180天为例,当单元A1和A2的备件数量为12时,系统任务成功率已达到96.53%;当备件数量为15个时,系统任务成功率为99.01%;当备件数量超过15个后,备件数量的增加对任务成功率的提高非常小。因此,需要在满足任务成功率要求的前提下合理配置备件数量,以提高备件保障的综合效益。 进一步,在固定备件数量的情况下,观察任务成功率随任务时间的变化情况。根据系统仿真模型,分别取单元A1和A2整机备件数量NA为0、2、5、10个,各仿真200 000次,得到系统的任务成功率随任务时间变化趋势如图4所示。 图4 系统任务成功率随任务时间的变化曲线Fig.4 Curve of the success rate of system mission as a function of mission time 图4反映了任务成功率随着任务时间的下降趋势。在单元A1和A2不配置备件时,系统的任务成功率下降最快,随着备件数量的增加,系统的任务成功率下降趋势变缓,反映出单元A1和A2的备件数量对系统任务成功性的影响较大。 由于在仿真过程中,单元A1和A2工作状态和维修状态持续时间、单元B工作状态持续时间都是随机生成的,因此每次的仿真结果都具有一定的随机性。根据大数定律可知,当仿真次数R足够大时,就可以用任务成功次数Rs与仿真次数R的比值近似表示任务成功率,且仿真次数R越大,结果越稳定。 为了定量分析仿真次数对计算结果的影响,考虑单元A1和A2备件数量无限、任务时间为180天的情形,分别将仿真次数取为20 000次、100 000次和200 000次,然后在不同仿真次数下各运行100次,得到一组该仿真次数下的任务成功率向量。结果表明,当仿真次数为20 000次时,任务成功率的极差为2.45×10-3,方差为1.02×10-6;当仿真次数为100 000次时,任务成功率的极差为1.39×10-3,方差为2.81×10-7;当仿真次数为100 000次时,任务成功率的极差为0.40×10-3,方差为2.07×10-8。这一结果与定性分析的结论一致,表明若想获得更加准确、稳定的任务成功率结果,应当选取较大的仿真次数。 在多状态系统的任务成功性评估问题中,单元状态数量的增加可能导致仿真变量的快速增多。本文以舰船多状态系统任务成功性评估为背景,通过分析系统状态持续时间分布和状态转移概率,建立了系统状态转移模型,并分析了使用规则、维修时间和保障资源约束的作用机理,建立了任务成功性仿真模型。示例分析表明,所构建的多状态任务成功性仿真评估方法可以较好地解决多状态系统使用、维修和保障资源约束难以解析描述,常规仿真算法工作量大的问题。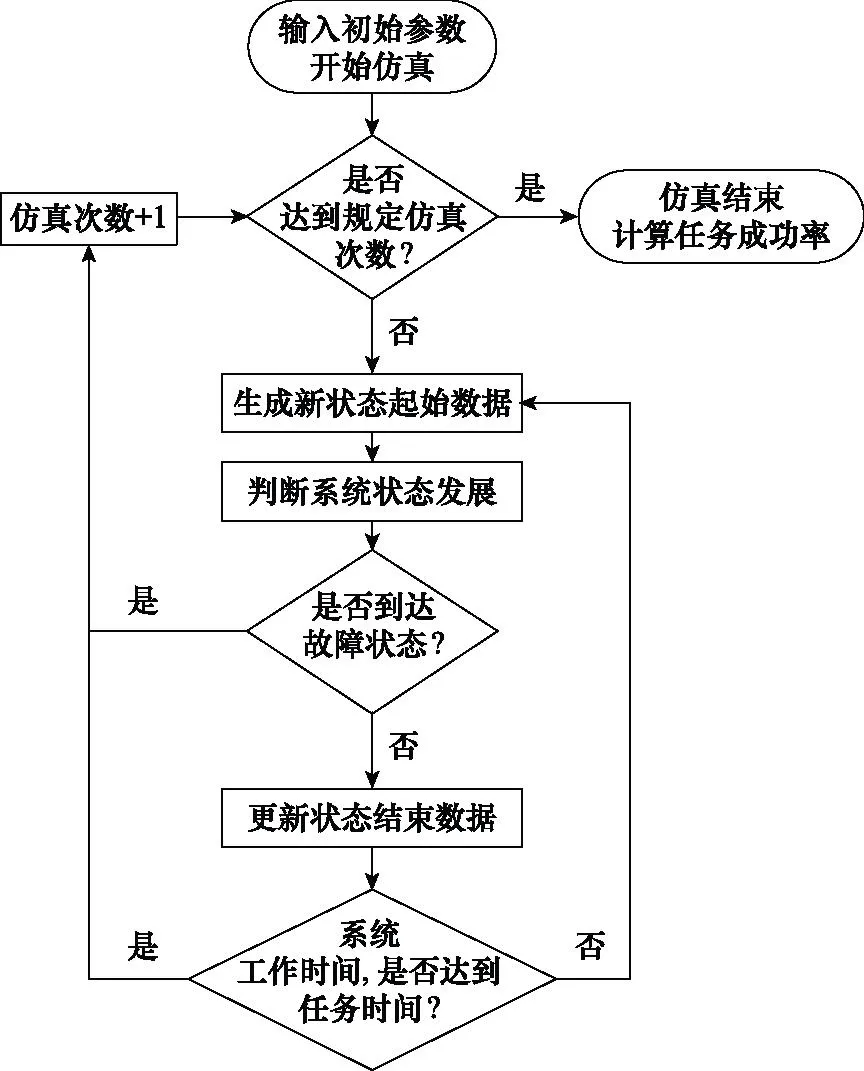
5 示例分析
5.1 使用和维修约束对系统任务成功性的影响
5.2 备件数量对系统任务成功性的影响
5.3 仿真次数对计算结果的影响
6 结 论
