基于电子商务竞标结构的分布式作战资源调度
2024-01-16刘丙杰陈建华
颜 骥, 刘丙杰, 陈建华
(海军潜艇学院战略导弹与水中兵器系, 山东 青岛 266199)
0 引 言
技术的进步使得现代作战资源具备对敌攻击、监视与侦察、搜索、救援以及灾难应对等多领域作战能力,如何充分发挥资源的能力是指挥员面临的巨大挑战。指挥员需要在有限的时间内,在任务时间、距离、优先级及资源能力等因素的约束下,将作战资源分配给不同的作战任务,并确定基于连续时间的资源调度计划,以最大化资源整体效用。任务分配与调度问题可视为约束优化问题[1],视约束条件和优化目标不同,问题存在多种变体,一般都将任务集映射为非循环图上的节点集,通过寻找资源的最优路径/调度求解问题。
本文主要研究上述问题的变体之一:带时间窗约束的团队合作定向问题[2](cooperative team orienteering problem with time windows, CTOPTW)。
定向问题(orienteering problem, OP)描述为:给定n个节点,每个节点i有一个非零分数s,节点i和j之间的弧有一关联成本cij,用节点间的旅行时间表示,每个节点最多被访问一次。OP的目标是在不违反最大成本约束T(旅行时间)的情况下,最大化路径得分,该路径由从节点1开始到节点n结束的节点子集组成。
团队OP(team orienteering problem, TOP)通过为多个定向选手创建网络的多个回路来扩展OP,以最大化团队得分。
带时间窗约束的[3-4]TOP(TOP with time windows, TOPTW),要求各选手在时间窗内访问节点,在时间窗之前或之后到达都不算节点被访问。
在TOPTW中,各选手遍历的节点并无交集,CTOPTW则要求多个选手在时间窗内同步访问节点,因而又称带时间窗与同步访问约束的路径规划问题[5](vehicle routing problem with time windows and synchronized visits, VRPTWSyn)。
CTOPTW模型目前广泛应用于家庭健康护理[6-7]、无人机任务分配与调度[1,8]以及应急物流管理[9-11]。现代战争中,大部分作战任务需要多个资源合作完成,如对潜艇搜索、攻击任务中,需要舰载直升机、水面舰船、潜艇甚至太空侦察卫星在指定时间窗内进行合作[12-13]。现代战争作战任务地理空间分布广,作战资源分属不同作战集群,前述问题求解方法并不适应现代作战任务分配与调度的需要。
针对作战任务CTOPTW特点,本文提出一种基于市场机制的分布式资源分配架构,将任务规划者视为消费者,将资源管理者视为供应商,供应商通过对消费者任务的去中心化竞标来协调跨多域的资源,使资源服务于需求最迫切、成本最低的客户。基于市场机制资源分配架构,提出规划时间可接受的资源联合调度(resource united scheduling, RUS)算法。
1 电子商务竞标结构
1.1 相关概念与假设
基于电信网络,消费者通过虚拟地指定商品名和条件,就可以从一系列供应商中选择最便宜的商品,这就是电子商务。资源获取渠道的丰富程度和速度,是电子商务的主要特征。
电子商务通过3个主要组成部分定义:通信系统、数据管理系统和安全机制[14]。假设通信及数据管理系统都是可靠的,本文重点介绍供应商与消费者之间的分布式资源分配架构,定义消费者和供应商之间的交互协议,以及基于用户安全考量,限定网络中的通信内容。
不同于经典市场特征,本文基于如下假设:① 消费者和供应商不用金钱交换服务,消费者通过赋予价值来表达其对某项任务的重视程度。② 消费者是诚实的行为人,不会为骗取供应商的资源而赋予低优先级的任务高价值。③ 供应商在其调度计划可行的情况下总是愿意为任务请求提供服务。当部分供应商忙于其他供应商时,会通过其提供的资源成本来表示这一状态。
1.2 消费者-供应商关系
本文关注供应商如何更有效地将有限的资源分配给消费者。两者间的互动由消费者开始,处于不同位置,需要特定资源的任务由多个消费者创建,位于不同地点的多个供应商负责提供并调度资源。任务由以下参数定义:
价值:指定的数值,位于区间[1,100]内,以量化任务的重要性。
位置:任务的二维地理坐标。
最小持续时间:完成任务所需的最少时间。
时间窗:必须为任务提供服务的开始和结束时间。如果资源在时间窗开始前到达,必须等待至时间窗开始才能服务任务。如果资源在任务窗口结束前未提供最小持续时间的服务,任务视为未完成。
资源:完成一项任务可能需要一种或多种资源。这些资源由类型定义,只有同类型的资源才能满足任务对该类资源的请求。
元素:每种类型的单个资源。
由上述定义可知,要完成一项任务,其请求的所有资源在该任务的时间窗内都必须处于相同的服务位置,且为任务提供服务的重叠时间不小于任务的最小持续时间。
消费者与供应商的关系决定了资源的调度方式,两者间的关系可概括为如下3种。
1.2.1 一个消费者对应一个供应商
一个消费者分配给一个供应商,这种烟囱式的关系今天仍然很普遍,因为其能简化调度,并且对计划细节保密。消费者的资源来源只有一个,所以任务的可行性很容易通过询问供应商是否拥有所需的资源,或是否正服务于另一任务来确定。由于资源只服务于一个客户,因此只有该消费者知道供应商的计划。
这种关系的最大缺点是消费者完全依赖于供应商。当任务需要的资源供应商无法提供,且没有其他选择时,任务便无法完成。并且,这种关系也会被对手观察到而变得易受攻击。即便通信链路上没有发布任何信息,对手也可以通过消费者-供应商的历史关系或观察供应商资源的活动来预测作战行动,甚至可以移除供应商来彻底削弱消费者。
1.2.2 一个消费者对应多个供应商
众多供应商能有力改进任务规划的效率。更多的供应商带来更多的资源可用性,增加了消费者获得所需资源的概率,该关系的另一优势是不可预测性。由于资源的丰富性,消费者可以改变对供应商的选择,来掩盖针对对手的行动意图,并通过冗余消除单供应商的不足。
但网络中节点越多,系统信息泄露的潜在风险就越高,对作战安全威胁也越大。因此,本文中,供应商不与彼此或消费者共享调度计划。供应商只通过带有以下信息的“投标”来回应消费者:
成本:资源到达任务位置的花费,以旅行时间度量。
时间窗:资源到达和离开任务位置的时间。
资源:分配给任务的资源类型和数量。
1.2.3 多个消费者对多个供应商
理论上,多个供应商共同服务一个消费者是理想的状态,但在现实世界中,从网络上获得众多供应商的灵活性需要多个消费者相互竞争供应商的资源来实现。
本文中,消费者并不与其他消费者合作以实现全局最大任务完成率。消费者只关心自己任务的完成情况,在任务完成或竞标停止前,消费者将持续向所有供应商发送资源请求。
1.3 电子商务竞标结构
本文中,消费者负责陈述一项任务需要的资源类型、数量以及任务的时间窗,对资源的调度则由供应商负责。消费者就所需资源通过多轮竞标与供应商交互。每一轮竞标包括3次握手:① 资源请求由消费者连同任务的关键信息发送给供应商;② 供应商向消费者发送元素投标,表示资源可用性;③ 消费者向供应商发送投标确认,以接受或拒绝元素投标。资源竞标轮中的信息流如图1所示。

图1 一轮竞标中的信息流Fig.1 Information flow in one bidding round
发送资源请求后,消费者将收到来自供应商的资源元素投标,每项任务有3种投标结果。
(1) 不完全实现
任务请求的至少一个资源,没有收到投标。
(2) 完整的实现
从一个或多个供应商那里,获得完成一项任务所需的所有资源,且资源重叠服务时间不小于最小持续时间。
(3) 非同步的实现
一项任务从多个供应商收到所有资源请求的投标,但收到的投标有不一致的服务时间。
这3种不同的投标结果需要一个协议来处理,使所有任务在多轮投标结束前达到完整实现的结果。对此,根据不同的投标结果,设计消费者决策过程如图2所示。

图2 消费者决策过程Fig.2 Consumer decision process
1.3.1 不完全实现
对不完全实现情况,消费者重新广播原始任务请求,希望上轮繁忙的供应商在下一轮竞标中,其调度表中能产生新的空闲时间。因任务投标可能在上轮竞标中被拒绝,供应商在竞标轮中可以不断调整调度计划,如图3所示。

图3 供应商计划决策周期Fig.3 Supplier schedule decision cycle
1.3.2 完整的实现
在完整实现的情况下,消费者将以最低的成本选择需要的竞标组合。消费者应通知未被选择的元素投标供应商,将任务从该元素的调度表中删除。如果分配的资源突然不可用,消费者可以在下一轮招标中重新提交资源请求。
在消费者决策过程中需注意的是,图2中,“选择的投标来自同一供应商”,当单个供应商为一项任务提供所有资源时,在任务时间窗范围内,供应商可以调整任务的开始和结束时间,即使消费者接受了一个(或多个)对特定开始时间的投标,供应商也可以根据其认为合适的情况更改开始时间。如果先前商定的开始时间过于严格,供应商可能会放弃承诺,以支持新的更有价值的任务请求。
当消费者从多个供应商中选择资源时,有必要进行“保护时间窗”设置。因原始资源请求指定了任务时间窗,为供应商提供的资源给出了一个可能到达和离开时间的范围。一旦找到一组完全完成任务的投标,消费者就不希望这些资源的时隙被供应商改动,从而导致任务不同步。为防止出现此类情况,消费者将任务的时间窗口确认为所有元素竞标重叠的开始和结束时间。供应商通过消费者发送的招标确认信息,对更改了的任务时间窗做出相应更新。
1.3.3 非同步的实现
非同步的实现给消费者带来的挑战最大。由于供应商之间不进行沟通,需利用消费者重新广播的资源请求信息来协调供应商之间的调度计划。
消费者在决策过程中试图保持任务的可行性与资源同步的平衡。任务的时间窗口范围越宽,供应商将任务纳入调度计划中的可选项就越多,任务资源请求得到响应的可能性就越大。对供应商而言,拥有众多选择的缺点是,元素投标与其他调度计划未知的供应商保持同步的概率降低了。
为推动不同供应商的同步,消费者可采取“更新时间窗”策略。具体方法为:将任务原时间窗开始时间推迟至所有元素投标的第二最早到达时间。由于后续供应商数学模型将所有任务推进至尽可能早的时间进行服务,这意味着当收到一个投标时,消费者知道在不改变计划的情况下,资源的开始服务时间不能再向前移动,但可以向后移动。并且,在资源路径的后续部分仍有空闲时间的情况下,整个调度计划仍是可行的。
将开始窗口更新到投标的第二最早到达时间,对于同步供应商而不使调度计划成为次优解至关重要。从图4可以看出,即便在新时间窗内,所有4个元素标价的到达时间都不是同步的。供应商可能会将标价e1和e2的到达时间后推至与e3的到达时间相同,但e4的到达时间可能不会提前。在这种情况下,任务将再次进入“非同步的实现”状态,时间窗将缩短到e4的到达时间,然后任务预计将在所有元素投标中达到同步。

图4 更新时间窗口Fig.4 Update time window
任务的开始时间不会立即更新为投标最迟的到达时间,即e4的到达时间,因为这可能会将任务的时间窗口收紧到一个不可行的时间范围。假设一个供应商提供投标e1和e2,其有一项非常有价值的任务,在任务i之后服务,但不能移动该任务。如果时间窗口大幅收紧,那么任务i将失去两个元素的投标。通过多轮投标逐步更新时间窗口,接下来的几轮可以让e4的供应商将其到达时间提前,或者新的供应商能够代替e4的供应商为任务i提供服务。
如果“更新时间窗”的过程导致一个供应商放弃对该任务的元素投标,而没有其他供应商填补,那么该任务将成为一个不完全实现的任务,消费者可沿用任务的原始时间窗重新提交资源请求。
2 供应商、消费者调度问题模型
2.1 供应商调度问题模型
文献[15-16]建立了单个供应商调度问题数学模型。首先定义集合、决策变量和输入变量的符号,然后介绍目标函数和约束条件,最后引入该模型的变体,以提高特定任务的元素竞标的同步性。
2.1.1 集合定义
T:所有任务集合。
U:所有资源集合。
U(e):所有元素e集合。
P:路径中所有位置集合。
集合P是资源执行的所有任务在路径上的位置集合,位置表示任务在路径中的顺序。如一项任务处于位置3,那么该任务是该资源将执行的第3个任务。
2.1.2 决策变量
accommodatei,u,p:二元决策变量,如果资源u在位置p上容纳了任务i,则为1,否则为0。
traveli,j,u:二元决策变量,如果资源u经任务i与任务j间的路径达到任务j,则为1,否则为0。
arrivei,u:连续决策变量,指定资源u到达任务i的时间。
departi,u:连续决策变量,指定资源u离开i的时间。
决策变量accommodate表示供应商暂时将资源分配给任务,任务是否执行最终由消费者决定。
2.1.3 输入变量
oi:任务i时间窗开始时间。
ci:任务i时间窗结束时间。
ai:任务i的最小持续时间。
horizon:规划周期。
ti,j,u:资源u从任务i移动到任务j的时间。
travelToBaseTimei,u:资源u从任务i移动到u的供应商位置的时间。
resourceCounti,e:任务i请求的元素e的个数。
valuei:任务i的价值。
2.1.4 目标函数
目标是使完成的任务总价值最大,每项任务有不同数量的资源请求,一些任务只请求一个资源,而另一些任务请求多个资源。只有获得了请求的全部资源,任务才能实现价值,因此,需用任务的价值除以其请求的资源数量。
由于供应商试图将尽可能多的任务打包到调度表中以最大化目标函数,资源的时间窗通常只持续最小持续时间,即便在该任务和下一任务之间有空闲时间,对于需要多个资源协同的任务,不同供应商提供的服务时间可能位于任务时间窗的不同位置,使任务依然得不到同步服务,如图4所示。为解决该问题,将最大时间窗口(maximum time window, MTW)概念添加到供应商调度模型中,以增加元素服务时间重叠概率。MTW目标函数为
目标函数通过最大化资源服务任务的离开时间和到达时间之差来最大化投标的时间窗口。参数wtimeWindow是拉伸时间窗的权重,用于调整容纳任务的数量与最大化任务的时间窗之间的关系。
2.1.5 约束条件
(1) 确保任务i不被其未请求的资源u容纳。
accommodatei,u,p=0, ∀i∈T;e∈i;u∉U(e);p∈P
(1)
(2) 每项任务i,每个资源只能为其分配一个位置。
accommodatei,u,p≤1, ∀i∈T;u∈U
(2)
(3) 每个位置p,每个资源只能分配一项任务。
accommodatei,u,p≤1, ∀u∈U;p∈P
(3)
(4) 确保每项任务i获得的元素e的个数不超过其请求数。
(4)
(5) 确保任务在资源路径上的位置是连续的。

∀u∈U;p∈P-1
(5)
(6) 在先后执行的两项任务之间强制存在一条旅行路径。
accommodatei,u,p+1+accommodatej,u,p-2traveli,j,u≤1,
∀i∈T;j∈T;∀u∈U;p∈P-1
(6)
(7) 如果容纳任务i,资源必须在任务时间窗开始后到达。
(7)
(8) 如果容纳任务i,资源必须在任务时间窗结束前离开。
∀i∈T;u∈U
(8)
(9) 资源在服务任务最小持续时间之后才能离开。
(9)
(10) 资源从供应商基地位置处开始调度。
travelToBaseTimei,u≤arrivei,u, ∀i∈T;u∈U
(10)
(11) 资源在供应商基地位置处结束调度。
departi,u≤horizon-travelToBaseTimei,u, ∀i∈T;u∈U
(11)
(12) 确保任务之间有足够的旅行时间。
(12)
(13) 将未被容纳的任务元素的时间窗强制为零。
∀i∈T;u∈U
(13)
MTW模型不能保证服务于同一任务的多个资源将同步到同一到达时间。为确保多个资源的同步,引入两个全局决策变量及3个约束条件,全局决策变量如下。
Arrivei:连续决策变量,指定请求的所有资源到达任务i的时间。
Departi:连续决策变量,指定请求的所有资源离开任务i的时间。
以上全局变量保证所有服务任务i的资源在至少最小持续时间的重叠时间窗内服务任务i。资源可以在同步服务任务之前到达,也可以在同步服务任务之后停留,同步约束如下。
(14) 全局变量Arrivei是服务任务i的资源的最迟到达时间。
∀i∈T;u∈U
(14)
(15) 全局变量Departi是服务任务i的资源的最早离开时间。
∀i∈T;u∈U
(15)
(16) 资源在服务任务最小持续时间后才能离开。
Arrivei+ai≤Departi, ∀i∈T
(16)
有约束式(16),约束式(9)变得冗余,可以从模型中移除。
2.2 消费者调度模型
消费者调度模型用于单个消费者为任务寻找最优的元素投标。
2.2.1 集合定义
T:所有任务集合。
B:所有元素投标集合。
B(i,e):对任务i投标的元素e的投标集。
2.2.2 决策变量
bidSelectb:二元决策变量,消费者选择元素投标b,则为1,否则为0。
performi:二元决策变量,消费者选择执行任务i,则为1,否则为0。
Arrivei:连续决策变量,指定投标开始任务i的时间。
Departi:连续决策变量,指定投标结束任务i的时间。
2.2.3 输入变量
earlyb:投标b开始服务任务的最早时间。
lateb:投标b结束服务任务的最迟时间。
costb:投标b的成本。
horizon:规划周期。
ai:任务i的最小持续时间。
resourceCounti,e:任务i请求的元素e的个数。
2.2.4 目标函数
目标是以最小的成本使完成的任务数量最多。当任务元素投标有多个出价时,模型选择使总成本最低的元素投标,成本由供应商定义。目标函数为
2.3.5 约束条件
(1) 确保每项任务i不会获得超出其请求的元素e的个数。
(17)
(2) 任务i获得请求的所有资源时才被执行。
(18)
(3) 全局变量Arrivei是为任务i选择的所有投标b的最迟到达时间。
earlyb·bidSelectb≤Arrivei, ∀i∈T;b∈B(i)
(19)
(4) 全局变量Departi是为任务i选择的所有投标b的最早离开时间。
lateb+horizon·(1-bidSelectb)≥Departi, ∀i∈T;b∈B(i)
(20)
(5) 任务在被服务所需的最小持续时间后才执行完毕。
Arrivei+ai·performi≤Departi, ∀i∈T
(21)
3 模型求解
以上模型为混合整数线性规划模型,其求解方法可分为精确求解和启发式求解方法。
定向问题是非确定性多项式(non-deterministic polynomial, NP)完全问题[4],这意味着,供应商调度问题也是NP完全问题,在问题规模较大时,精确解法在有限时间内无法给出最优解。在已知的组合优化问题中,大邻域搜索是解决混合整数规划问题最强大也最昂贵的启发式方法之一[17-18]。为利用大邻域搜索算法的优势,减少运算成本,本文将求解过程分为两个阶段[19-20],阶段一采用绩效(merit-based, MB)算法[9]构建问题的初始解,阶段二基于初始解采用自适应大邻域搜索(adaptive large neighborhood search, ALNS)算法寻找最优解。
消费者数学模型较简单,采用混合整数线性规划来求解。
3.1 ALNS
ALNS算法[21]基于大邻域搜索算法,通过在算法中引入多个破坏算子与修复算子扩大解的搜索空间,同时根据算子的历史表现自适应调整算子的权重来提高算法的搜索效率。
算法的终止条件一般为搜索迭代次数,符合终止条件后,算法返回全局最优解。
在迭代过程中若生成非改进解(即新解不优于当前解),ALNS算法采用模拟退火准则接受非改进解,避免算法陷入局部最优。
3.2 插入可行性判断
由于时间窗约束及同步约束,使得资源路径间高度依赖,任意路径上节点方向的任何微小变化都可能影响所有路径的到达时间和服务开始时间。为评估在常数时间内插入任意点的可行性,采取如下策略[5]。
首先,滤除解搜寻过程中任务间不可达的边,即对于任务i,j,当oi+ai+tij>cj时,将边arcij从初始解中移除。同样,由于部分任务需要多个资源服务,也就是说被多条路径访问,如果在某一路径中,任务j要在任务i之后被访问。而在其他路径中,任务j已被插入到任务i之前,对于这种情况,也要予以滤除。最终,可用一个由0-1变量组成的“插入可行矩阵”Ω来促进插入过程。
为在有限的计算时间内评估某一路径中插入操作的可行性,还需定义变量maxshifti。该变量用于计算在访问任务i之前的可用冗余时间。任务i的访问时间计算为
arrivei=departi-1+ti-1,i
(22)
对于要求多个资源同步服务的任务i,同步服务开始时间为
(23)
式中:Γ为所有服务任务i的资源路径。资源服务任务i的等待时间为
waiti=sync_starti-arrivei
(24)
将路径τ对任务i的访问定义为τ(i),在满足解可行前提下,资源访问任务i容许延迟的时间maxshiftτ(i)为
maxshiftτ(i)=min{cτ(i)-startτ(i),waitτ(i+1)+maxshiftτ(i+1)}
(25)
为计算maxshiftτ(i),需要从每条路径的最后一个任务开始算起,因资源返回基地的时间与其他任务无关。

(26)

(27)

3.3 初始解生成
本文参考MB算法构建ALNS算法的初始解。MB算法是一种改进节约算法[10],结合了经典节约算法和扫描法的优势,通过在节约函数中添加收益附加项来最大化全局收益。不同于经典节约算法,改进节约算法先尝试在路径终端插入新节点,若插入失败,则尝试将新节点插入路径之内[11]。MB算法的核心是优势对列表(merit pair list, MPL),MPL由元组〈i,j,Mij〉构成,其中i,j∈v,优势值Mij计算如下:

(28)


算法 1 MB算法伪代码输入 最优收益α, 最优路径β, 未分配任务集T, 优势对列表MPL, 任务m价值ψm, 元素e个数Ue, 元素e路径数e∈U(ne), 任务m的资源需求数mrm, 任务距离矩阵dt×t, 任务q的前序已分配任务q'输出 β和α1 function MB heuristic2 sort T in descending order of ψmrm, ∀m∈T3 generate dt×t4 calculate Ω5 calculate merit list and sort (
3.4 供应商投标决策过程
供应商在多轮竞标过程中需存储两个列表。
(1) 未确认任务列表:供应商在上轮调度中已分配,但未从对应消费者处收到接受或拒绝元素投标信息的任务列表。
(2) 确认的任务列表:供应商已从对应的消费者处收到元素投标接受的任务列表。
为加快算法的运行时间,上述列表还包含何种资源在何时为哪项任务提供服务的信息,这些信息被用于下轮投标时初始解的构建。通过将表内任务插入曾经的最优资源路径位置,使得本轮投标能利用前几轮投标的结果。当任务因消费者拒绝招标而移除,或消费者对招标资源采取“更新时间窗”策略时,资源调度将发生变化,但原调度框架仍能极大地改善下轮投标的运行时间。
在首轮招、投标中,上述两个列表为空,首轮招、投标结束后,供应商更新其资源调度表和上述任务列表。当供应商找到资源调度新的最优解后,将调度表中的任务与两确认列表进行比较,可能出现以下3种情况,如图5所示。
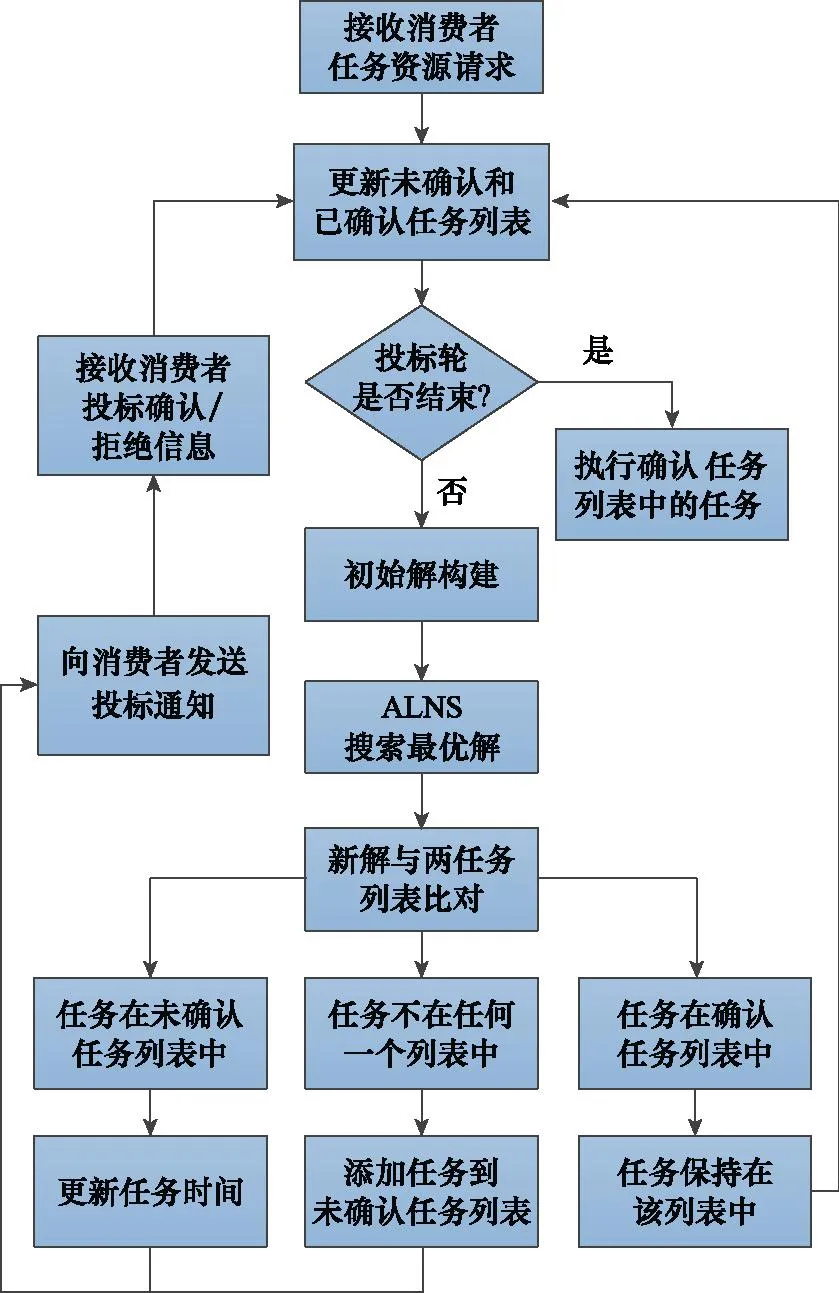
图5 供应商决策过程Fig.5 Suppliers decision process
(1) 任务不在任何一个确认列表中:该任务将被添加到未确认任务列表中,并向消费者发送供应商投标通知。
(2) 任务已经在未确认任务列表中:任务的到达和离开时间将在未确认任务列表中更新,以同步新资源调度表的变化。消费者将再次收到供应商的投标通知。
(3) 任务已经在“确认任务列表”中:将任务保持在该列表中,因消费者已经确认了任务投标,供应商不再向消费者发送任何消息。
供应商大规模邻域搜索中的破坏算子和修复算子见文献[9],此处不再赘述。
3.5 算例分析
3.5.1 测试集
为分析本算法,建立4个伪随机检验集,对算法进行4轮测试。任务资源需求集为{1,2,3,4},其中{1}是单资源服务任务,{4}是需要4个资源同步的任务。在每个测试集中,需要各级别同步的任务数量相等。如果一个测试集中有4个单资源任务,也会有4个双协同任务,依此类推。4轮测试由消费者的任务计数区分,分别为4,8,12,16。
测试集的数据由指定边界内的随机数生成器生成。任务区域为100 km×100 km的二维平面,任务位置的经纬度是在范围[0,100]内随机生成的数字对,任务值从U[1,100]中随机选取。完成所有任务的规划时限为1 000 min,所有任务要求完成服务的最短时间都为25 min,任务时间窗开始时间从[0,900]min的均匀分布中选择,所有时间窗结束时间都是在所选开始时间之后的50 min。
对于任务请求的每个资源,其类型从集合{A,B,C,D}中随机选择。因此,一项请求4个资源的任务可以赋予该集合的任意组合,如{A,A,A,A}或{A,B,C,D}。所有资源移动速度相等,但只有X类型的资源才能满足X类型的任务请求。
与任务位置相同,供应商基地位置也随机产生。由供应商控制的所有资源,其规划都从供应商基地位置处开始,又在该处结束。供应商从资源类型集合{A,B,C,D}中随机分配4类资源。因此,供应商的资源可能为从{A,A,A,A}到{D,D,D,D}之间的所有排列。
3.5.2 评估测试
测试中消费者-供应商网络为两个供应商对应3个消费者。消费者和供应商都从测试数据集生成任务和资源。为确定哪种方法更适合实战场景下的调度资源,通过分析两个特征进行比较:① 方法的运行时间;② 最佳调度值。
正如预期的那样,在表1中,除一个测试集外,RUS在比混合整数线性规划(mixed integer linear programming, MILP)更短的时间内求解测试集。

表1 算法运行时间比较Table 1 Algorithm run time comparison s
一般情况下,随着测试集规模的增加,MILP方法将无法在2 h内找到最优解,而RUS方法能在合理的时间范围内持续地找到解。尽管MILP方法不像RUS方法那样需要多轮竞标,但在每个消费者完成8项任务后,MILP方法就变得难以处理。
最优性比较的目的是确定RUS方法生成的解与最优解的差距。MILP方法需要搜索整个解空间,但能保证找到最优解。最优性差距显示了MILP方法找到的最优解与RUS方法的解之间的差异。
表2中的数据表明,RUS方法提供的解接近最优解。在MILP方法能在2 h内找到最优解的12种情况中,只有1种情况是RUS方法无法找到的。此外,在该情况下,RUS方法解与最优解之间的差异只有4%。

表2 最优性比较Table 2 Optimality comparison
4 结 论
本文参照市场机制,建立基于电子商务多轮竞标的供应商调度架构,消费者向供应商提交资源请求参数,供应商对各资源请求发起投标,其资源调度计划和成本函数仅消费者请求部分对消费者可见,并允许消费者从相互独立供应商处同步资源。消费者使用混合整数线性规划来选择成本最低的投标,通过这些投标的组合来满足任务的需求。
本文基于电子商务架构的作战资源调度,将作战资源调度和作战任务创建与规划分由作战资源规划节点和作战任务规划节点承担,作战资源规划节点只关心本基地所辖资源的调度,作战任务规划节点也只关注本区域要执行的作战任务及任务资源需求。通过去中心化的资源调度与任务规划,减轻了集中式作战规划的复杂性和易损性。同时,供应商不与彼此或消费者共享调度计划,而只通过有限的握手信息进行交互,减少作战网络上的信息传输,防止被敌窃听而泄露计划。建立了供应商和消费者调度数学模型,并根据模型特点提出模型求解方法,算例分析验证了方法的有效性。
