基于目标暴露区的地面防空兵力最佳配置区规划

曹 原, 寇英信, 李勇祥

(1. 空军工程大学航空工程学院, 陕西 西安 710038; 2. 中国人民解放军95261部队, 广西 柳州 545000)

0 引 言

敌航空兵在远距离支援干扰掩护下对地面防空兵进行突防是典型的空袭作战模式,远距离支援干扰具有干扰功率大、干扰压制频带宽、干扰空间指向性强等优势,地面防空兵在强电磁干扰压制环境下由于无法有效获取空中战场态势信息,造成地面防空作战效能急剧下降甚至造成战斗失利[1]。因此,在远距离支援干扰条件下地面防空兵有效抗干扰是防空作战面临的难点问题。

目前,抗远距离支援干扰主要包括技术抗干扰和战术抗干扰两类方法,当技术抗干扰效果不佳时,可采取战术抗干扰,两者互为补充。其中,技术抗干扰是基于防空导弹雷达本身的抗干扰特性和能力,对压制干扰通过功率对抗[2-3]、波形选择[4-5]、频率捷变[6-8]、信号滤波算法[9]等进行反制。战术抗干扰[10]是在统一指挥机构的协调下,通过发挥地面防空的体系优势而实施的抗干扰手段,如外部情报信息支援、空中干扰源交叉定位等。其中,战前科学合理的地面防空兵力配置[11]是战术抗干扰的一种重要途径,目前的直接相关文献较少。在电子干扰支援的空袭背景下,依据掩护角、配置距离、有效干扰的相互关系,以杀伤区面积为目标函数,构建地空反辐射混编群兵力配置优化模型,该模型印证了混编群兵力优化配置方法的有效性[12]。在远距离支援干扰的条件下,以雷达基本原理和干扰方程为基础构造雷达探测距离模型,并推算在不同的抗干扰措施下雷达探测范围方程[13]。评估远距离支援干扰作战效能的关键是准确计算出在不同条件下干扰压制区形状和大小,故得到准确计算干扰压制区的方法,该方法可有效描述出雷达的动态压制区域,并结合几种典型雷达特征参数检验方法的可行性[14]。针对支援突防作战中远距离支援干扰机最优空域的规划问题,确定干扰机的配置范围、雷达探测范围,提出航线安全间隔和有效干扰航段的概念。在远距离支援干扰压制下,地面防空武器系统雷达的探测距离被极大地压缩,但仍然存在由于地面防空雷达烧穿距离所形成的敌机暴露区[15]。针对非线性规划数学模型的快速求解难题,萤火虫优化(glowworm swarm optimization,GSO)算法因具有结构简单、控制参数少、易于实现的特点而得到广泛的关注和应用,但其易陷入局部最优导致过早收敛,从而影响寻优精度[16]。故本文采用基于线性递减权重函数改进的GSO (improved GSO,IGSO)算法,避免其快速陷入局部最优而无法找到全局最优的问题。

目标暴露区是地面防空雷达在遭受远距离支援干扰条件下能够发现和跟踪被干扰掩护敌机的区域,基于此区域可构建地面防空兵力的可配置区,在该区域不同的地面防空兵力配置可形成不同的战术抗干扰效果。本文基于地面防空兵力干扰威胁指数最小构建目标函数及其兵力配置约束条件,从而可得到最优的地面防空兵力配置方案。

1 远距离支援干扰战术运用分析

1.1 远距离支援干扰“三点一线”运用模式

远距离支援干扰机掩护攻击机对地面防空兵力实施正面突防时,其战术运用基本特点是力求构成干扰机、被掩护攻击机和地面防空兵力的“三点一线”干扰态势,使得干扰能量能够注入地面防空雷达主瓣造成接收机饱和。通常远距离支援干扰机对防空雷达的最小有效干扰距离在其发射区近界以内[17-18]。

如图1所示,远距离支援干扰压制中心线为干扰波束的法线,等效为远距离支援干扰机与拟突防地面防空武器的连线[19-21]。实施干扰时,被掩护攻击机处于压制中心线附近,此时干扰机形成主瓣干扰走廊并处于最佳干扰阵位。

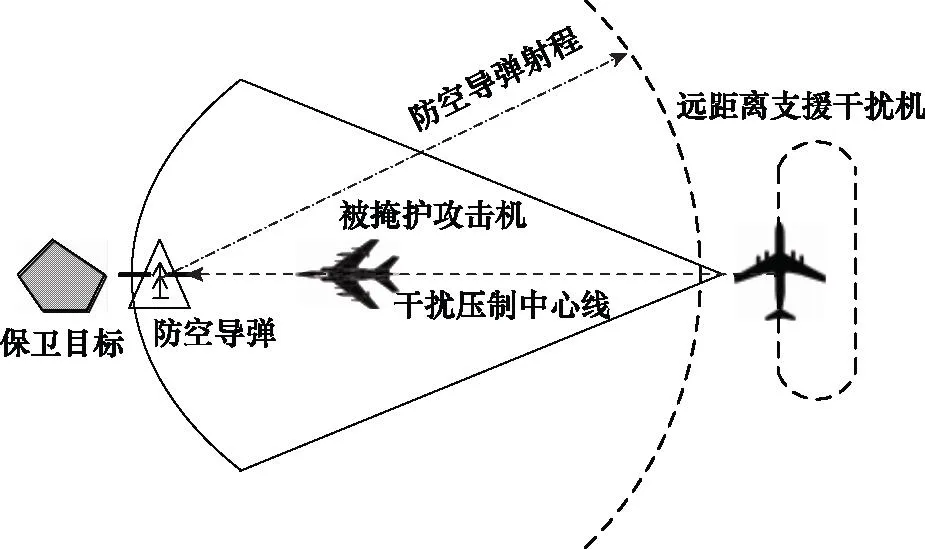
图1 “三点一线”远距离支援干扰模式Fig.1 “Three points one line” stand-off jamming mode

1.2 远距离支援干扰目标暴露区

目标暴露区是在干扰条件下地面防空雷达可发现被掩护目标的区域,该区域之外是干扰压制区,暴露区的大小与干扰强度、地面防空雷达及被掩护目标有关。

假设干扰机、地面防空雷达的位置相对固定,被掩护攻击机为运动目标,三者的空间位置关系如图2所示。

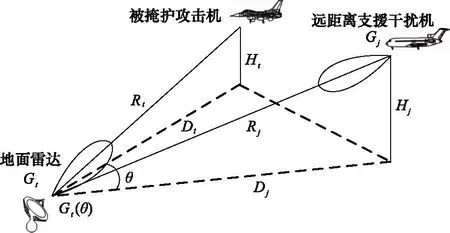
图2 远距离支援干扰示意图Fig.2 Schematic diagram of stand-off jamming

当地面防空雷达对攻击机探测跟踪时,雷达对攻击机和干扰机的水平张角为θ。设干扰机和攻击机飞行高度分别为Hj和Ht,两者距地面防空雷达的距离分别为Rj和Rt。显然,地面防空雷达将同时接收到攻击机的目标回波信号Prs和干扰机施放的干扰信号Prj。由雷达方程可知地面防空雷达接收目标反射的回波信号Prs为

(1)

式中:Pt为地面防空雷达发射功率;Gt为雷达天线主瓣增益;σ为目标雷达截面积;Rt为目标至地面雷达的距离;λ为地面雷达波长;A为地面雷达接收天线的有效面积。

由干扰机施放的干扰信号Prj为

(2)

式中:Pj为干扰机的发射功率;Gj为干扰机天线增益;γj为干扰信号对雷达天线的极化系数;A′为雷达天线在干扰机方向上的有效接收面积;Gt(θ)为与之对应的雷达天线在干扰机θ方向的增益,根据经验Gt(θ)[22-23]可表示为

(3)

式中:θ0.5为水平方向雷达半功率波瓣宽度;q为常数,取[0.04,0.1]。通常用压制系数Kj对雷达的干扰效果进行衡量,表示对雷达实施干扰致使其发现目标概率下降至10%时所需的最小干扰信号与目标回波信号比值,该区域为干扰压制区。当压制系数小于Kj时所形成的区域是目标暴露区,可表示为

(4)

2 远距离支援干扰条件下的防空兵力可配置区规划

2.1 基于目标暴露区的兵力可配置区计算

远距离支援干扰机在主攻方向对攻击机进行掩护,通过对地面防空雷达系统实施干扰形成干扰走廊。当突防方向上的火力单元受到干扰压制时,友邻火力单元需要配置在一定区域内防止受到干扰压制并能够进行火力补充,以阻止敌机突防。此种情况下,友邻火力单元、被掩护攻击机及干扰机位置关系如图3所示。

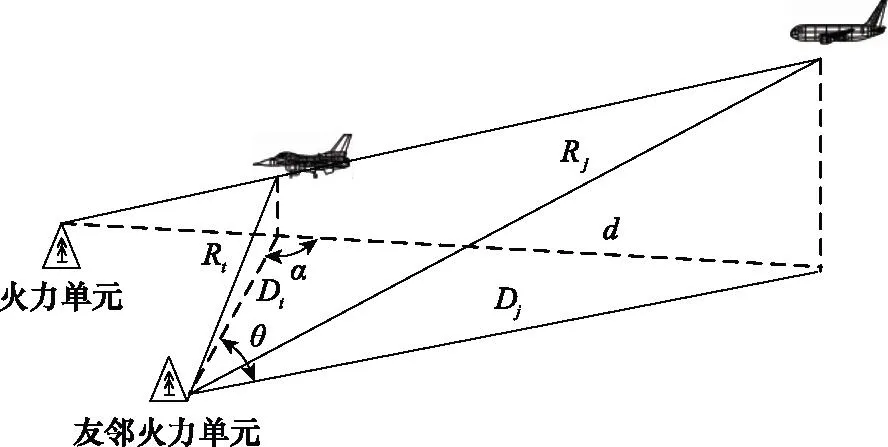
图3 友邻火力单元、攻击机和干扰机位置关系Fig.3 Position relationships of neighboring firepower unit, attack aircraft and jammer

设干扰机飞行高度为Hj,被掩护攻击机飞行高度为Ht,干扰机和被掩护攻击机距友邻火力单元的距离分别为Rj和Rt,则有

(5)

(6)

讨论远距离支援干扰机对友邻火力单元的干扰压制区,需要根据Dt及θ变化情况综合分析。一般情况下θ∈(θ0.5/2,π/2),根据式(3)可知,友邻火力单元雷达在干扰机方向上的增益为

(7)

(8)

(9)

即

(10)

讨论式(10)在等式成立的情况下Dt随α变化范围,可建立以被掩护攻击机O为极点,指向干扰机方向OJ为极轴的坐标系。在该极坐标系中可绘出f(Dt,α)=A曲线,A在干扰机、被掩护攻击机以及雷达参数确定情况下为常数。如图4所示,得到关于极轴对称的鞋底形曲线,在曲线范围内为被掩护攻击机的暴露区,友邻火力单元配置在此区域不受干扰压制。考虑地空导弹武器系统最大航路捷径Pmax的限制,友邻火力单元可配置区为阴影区域。

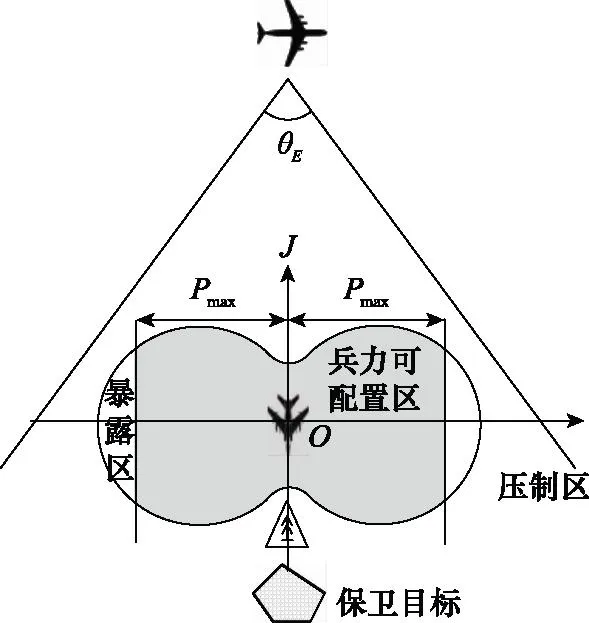
图4 基于暴露区的兵力可配置区Fig.4 Force configurable area based on exposure area

2.2 可配置区内地面防空兵力配置间距计算

在地面防空兵力可配置区,为避免多个火力单元同时被干扰压制,应充分利用各火力单元的目标暴露区,科学规划各火力单元的横向和纵向配置间距,以利于形成有效打击态势[24-25]。

2.2.1 横向配置间距计算

多个火力单元线形配置时如图5所示,友邻火力单元与干扰机、被掩护攻击机三者夹角α应不小于防空雷达在定位平面上的方向图宽,此时地空导弹武器系统等效门限的干扰功率密度大于或等于干扰机干扰功率密度,且友邻火力单元能从雷达荧光屏中将敌机分辨出来。因此,友邻火力单元配置距离应根据角度α及火力衔接要求确定。远距离支援干扰机对某一火力单元实施主瓣干扰时通常也对临近一侧火力单元雷达旁瓣进行干扰。要使临近一侧的火力单元能够杀伤敌机,则要求其受旁瓣干扰时雷达稳定跟踪目标且距离大于发射区近界dfj。

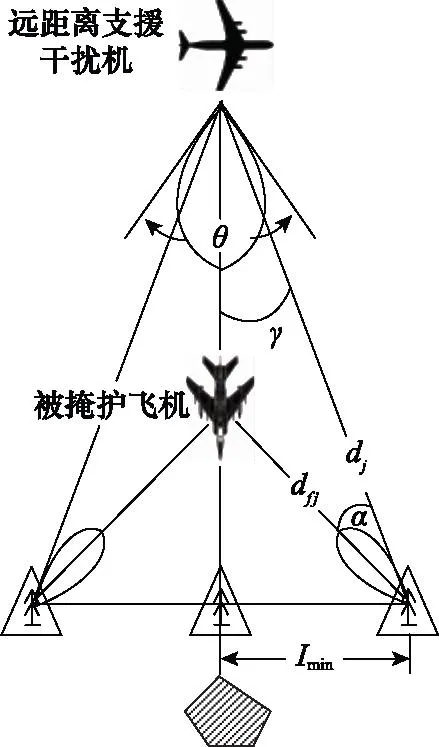
图5 横向配置距离Fig.5 Horizontal allocation distance

相邻两个火力单元之间的最小距离,可根据几何关系进行确定,则有

Imin=djsinγ

(11)

(12)

式中:dfj为地空导弹武器系统发射区近界;dj为干扰机与友邻防空单元之间的距离。

2.2.2 纵向配置间距计算

多个火力单元采用三角形或梯形配置时,前后间距应根据前端火力单元受干扰压制时后端火力单元的抗击能力确定。图6中,干扰机、被掩护攻击机与火力单元构成“三点一线”干扰态势时,后方火力单元应与前方火力单元保持一定间距,避免同时受到干扰压制,并满足火力支援的条件。

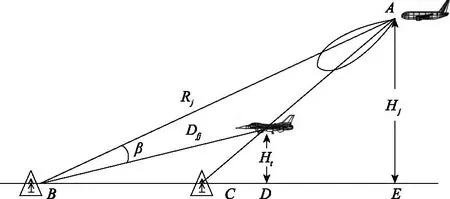
图6 纵向配置距离Fig.6 Longitudinal allocation distance

在后方火力单元受旁瓣干扰并且发现目标距离大于发射区近界时,相邻火力单元之间的最小纵向配置距离可由以下参数确定:

(13)

(14)

DE=BE-BD

(15)

(16)

(17)

式中:Rj为地面防空火力单元与干扰机之间的距离;Dfj为地面防空火力单元发射区近界。

2.3 基于雷达干扰扇面的干扰威胁指数计算

防空雷达受到干扰时,雷达显示器上的高亮扇区称为干扰扇面,干扰信号能够压制目标回波信号而呈现在显示器的扇面则称为有效干扰扇面[26-27],通常作为电子干扰效果的重要战术衡量指标。当火力单元配置在可配置区内不同位置点时,其雷达干扰扇面的角度大小也不相同,雷达干扰扇面角度越大则火力单元所受威胁就越大,本文用火力单元干扰威胁指数表述其在可配置区内不同配置点的雷达干扰扇面角度大小。

如图7所示,当干扰机对防空雷达进行干扰时,若要形成角度为θj的干扰扇面,则必须保证干扰功率以大于接收机内部噪声电平一定倍数的干扰信号电平从雷达方向图θ角(θ=θj/2)方向进入防空雷达接收机。

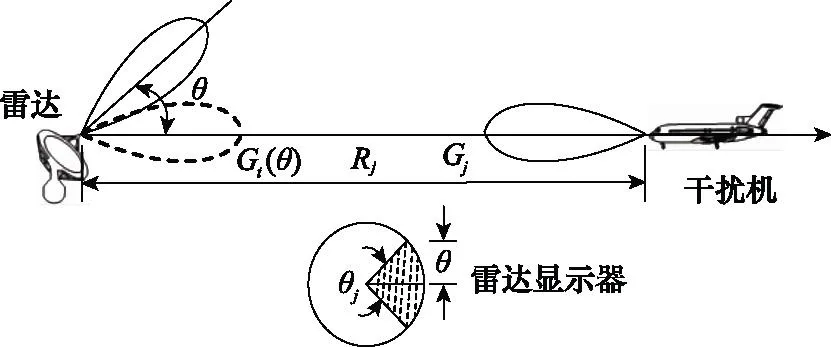
图7 雷达干扰扇面示意图Fig.7 Schematic diagram of radar jamming sector

考虑到干扰信号带宽的影响,进入防空雷达接收机的干扰信号功率为Prj,设Pn表示折算到接收机输入端的内部噪声电平,m表示倍数,若进入雷达接收机的干扰信号电平满足Prj≥mPn,则干扰机可在雷达环视显示器上形成θj角的干扰扇面,则有

(18)

可得

(19)

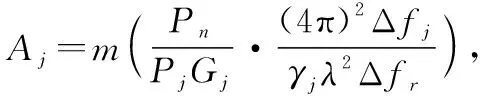
(20)

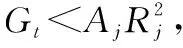
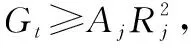
(21)

当π/2<θ≤π时,因Gt(θ)与θ无关,此时干扰机能够全方位干扰雷达,干扰扇面θj=2π。综上所述,得到干扰扇面的计算公式,将其归一化后得到干扰威胁指数模型为

(22)

3 远距离支援干扰下兵力最佳配置区模型建立与求解

地面防空各火力单元在进行部署决策时,应当保证各火力单元在可配置区内所遭受的干扰威胁指数总量最小,且各火力单元之间同时满足横向和纵向的配置要求,从而得到地面防空兵力的最佳可配置区,最大限度地削弱远距离干扰机所带来的不利影响,实现对来袭敌机的有效拦截[28]。

3.1 模型建立

假定敌攻击机在多个远距离干扰机掩护下从多个方向对我方地面防空阵地进行突防。各防空火力单元受到的总干扰威胁指数F模型为

(23)

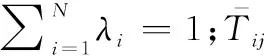
因此,远距离支援干扰条件下地面防空兵力最佳配置区决策的目标函数应为

(24)

设以骨干防空火力单元为原点建立直角坐标系,友邻的火力单元的坐标为(x1,y1,z1),假设远距离支援干扰机与攻击机的位置已知,坐标分别为(a1,b1,c1)和(a2,b2,c2),目标函数应满足以下约束条件。

(1) 基于目标暴露区的兵力可配置区。根据第2.1节,在图4的曲线范围内为被掩护攻击机的暴露区,友邻火力单元配置在此区域不受干扰压制。考虑地空导弹武器系统最大航路捷径Pmax的限制,友邻火力单元可配置区为阴影区,则有

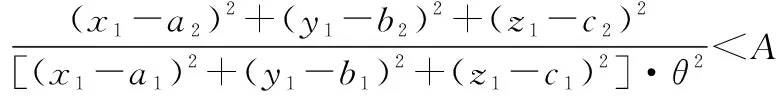
(25)

式中:θ可由余弦定理求得。

(2) 防空兵力横向配置间距。友邻火力配置距离应满足当骨干火力单元受到干扰压制时,友邻火力单元横向距离在干扰机压制近界以外,则有

|y1|≥djsinγ

(26)

(3) 防空兵力纵向配置间距。骨干火力单元与友邻火力单元纵向配置距离应大于干扰机压制区纵深,则有

(27)

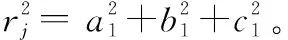
3.2 IGSO算法

根据第3.1节构造的远距离支援干扰下防空兵力配置模型,可知该问题是一个多约束非线性复合寻优问题,群体智能优化算法对该类数学问题的求解十分有效。GSO算法是模拟萤火虫发光行为的一种新型群体搜索随机优化算法[29-30]。

在GSO算法中,萤火虫i由当前位置xi(t)和萤光素值li(t)定义,并且该位置的目标函数值为f(xi(t))。GSO算法对决策域范围进行更新。

(28)

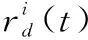
pij(t)表示在第t次迭代中,萤火虫i向其邻居萤火虫j移动的概率,计算公式如下:

(29)

萤火虫i移动后的位置计算如下,其中,s为移动步长:

(30)

萤火虫i移动到新位置后,将更新其萤光素值:

li(t)=(1-ρ)li(t-1)+γf(xi(t))

(31)

式中:li(t)为在第t次迭代中萤火虫i的萤光素值;ρ∈(0,1)为常数,与荧光素挥发有关;γ为常数,表示荧光素更新率。

在GSO算法中,随着迭代次数增加,萤火虫个体在后期逐步移动到全局极值点附近,个体之间的距离也逐渐缩小,根据位置更新式(30)可知,此时的萤火虫个体间相互吸引力变大,并且移动步长也较大,这会导致萤火虫个体在全局极值点附近来回震荡,无法收敛。

因此,本文提出基于线性递减权重函数的IGSO算法,其位置更新公式为

(32)

(33)

式中:ωmax和ωmin分别为最大和最小权重;n和nmax分别为当前和最大迭代次数。当权重较大时,萤火虫个体当前位置对下次迭代后的位置有较大的影响,个体之间的吸引力较小,更偏向于全局搜索,局部搜索能力较弱。权重变小后,个体更偏向于局部搜索,收敛性更强。因此,调整惯性权重ω(n),可在搜索的前期使萤火虫个体更加侧重于全局搜索能力,有利于扩大搜索范围、加快搜索速度。随着搜索进入后期,惯性权重也随之变小,此时萤火虫个体在较小的区域中增强局部搜索能力,避免步长过大而在全局极值点附近震荡。

3.3 IGSO算法的求解步骤

综合以上叙述,IGSO算法求解防空兵力最佳配置区域的步骤如图8所示。

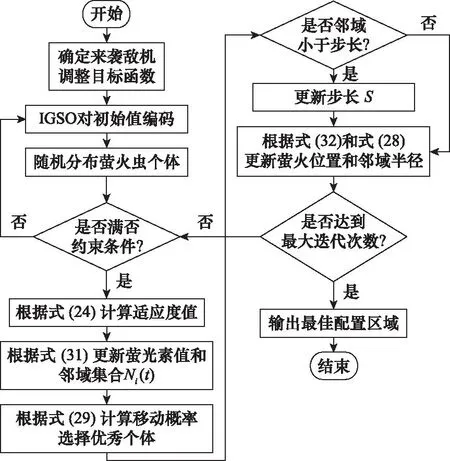
图8 IGSO算法流程图Fig.8 IGSO algorithm flow chart

具体的步骤如下。

步骤 1确定来袭远距离干扰机的干扰方向数、攻击机数量、位置信息以及干扰方向的权重并且调整目标函数参数。

步骤 2初始化IGSO算法中荧光素初始值γ、邻域变化率γ、萤火虫邻居数量阈值γ、移动步长γ、荧光素挥发系数γ、荧光素更新率γ、最大迭代次数nmax、最大权重ωmax以及最小权重ωmin,并判断在搜索空间中随机分布的萤火虫位置是否满足约束条件。

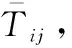
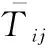
步骤 5利用式(24)计算每个萤火虫个体的适应度值,找到并保存当前群体中受威胁程度最小的萤火虫群体。

步骤 6利用式(28)和式(31)更新萤火虫个体的荧光素值和邻域集合,并以式(29)得到的概率向荧光素更强的萤火虫群体移动。

步骤 7判断萤火虫个体的决策范围是否小于步长,如果小于则需要更新步长,然后利用线性递减权重函数改进的式(32)更新萤火虫位置以及决策域范围。

步骤 8判断是否达到最大迭代次数,若达到,则输出最佳配置区域;若未达到,则重复执行步骤3至步骤7。

4 仿真分析

本文对基于目标暴露区的地面防空兵力最佳配置区规划模型进行仿真验证。首先,对IGSO算法的收敛性进行分析,初始参数如下:荧光素初始值l0=6,感知范围rs=5,邻域变化率β=0.08,控制萤火虫邻居数量的阈值nt=8,与荧光素挥发有关的ρ=0.5,荧光素更新率γ=0.7。最大迭代次数为100次,种群的数量为90,最大和最小权重分别为1.1和0.2。将式(24)计算的目标函数值作为萤火虫个体的适应度值,将GSO算法和IGSO算法的适应度值与进化代数之间的关系进行对比,分析两种算法各自运行40次所需的时间,结果分别如图9和图10所示。

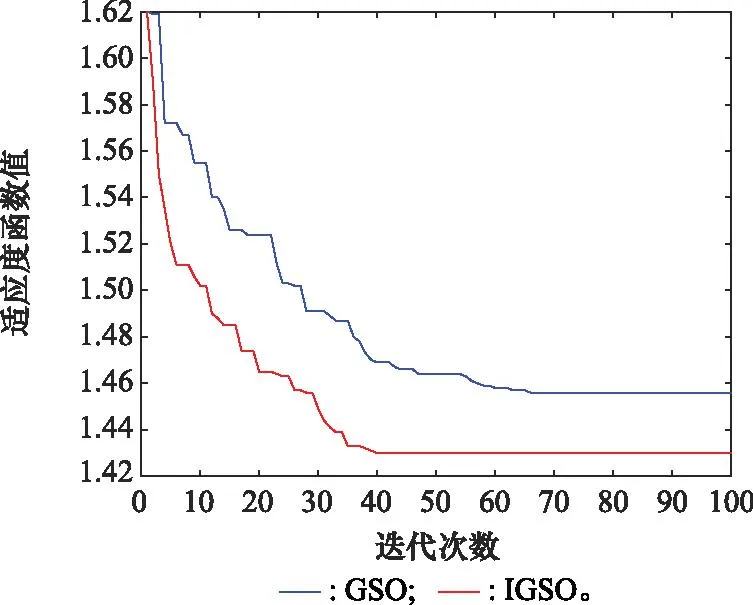
图9 IGSO和GSO算法进化过程对比Fig.9 Comparison of IGSO and GSO algorithm evolution process

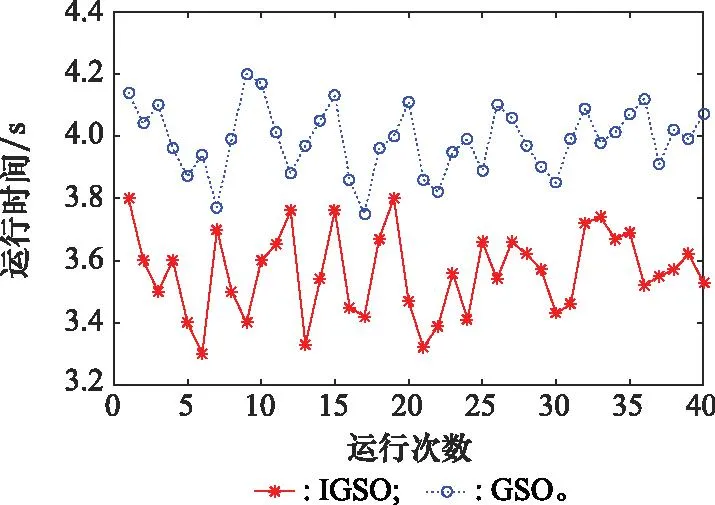
图10 IGSO和GSO算法运行时间对比Fig.10 Comparison of IGSO and GSO algorithm running time

从图9可知,IGSO算法迭代到40代时,适应度值趋于稳定,最佳值为1.43,但GSO算法迭代至70代左右才稳定,适应度值收敛到1.46。该结果表明,IGSO的寻优性能要强于GSO,陷入局部最优的概率较小。从图10可知,IGSO 和GSO运行40次的平均时间分别是3.562 s和3.989 s,IGSO以更快的收敛速度找到全局最优解。这是因为引入可变惯性权重有助于加快GSO算法的全局收敛速度,增强了在极值点附近的局部搜索能力,避免在极值点附近振荡。显然,IGSO弥补了GSO容易陷入局部最优值的不足,更加适合于求解本问题。

假设在某次作战中,有两架敌方远距离支援干扰机分别从不同方向对我方骨干防空阵地进行干扰压制,各掩护一架攻击机进行突防。两架干扰机的位置坐标分别为(254,225)、(198,313),飞行高度均为8 km,攻击机的坐标分别为(212,181)、(159,248),飞行高度为5 km,骨干防空火力单元的坐标为(105,117),两条突击方向权重一致,即λ1=λ2=0.5。干扰机参数和地面防空雷达参数如表1和表2所示。

表1 远距离支援干扰机性能参数Table 1 Long range jammer performance parameters

表2 防空雷达性能参数Table 2 Air defense radar performance parameters

从图11可以看出,我方骨干防空阵地被两批次来袭敌机从不同方向逼近,骨干防空火力单元遭到电子干扰机的压制,形成一个以曲线外为干扰压制区,曲线以内为目标暴露区的对称心形曲线。基于第2节防空兵力配置区规划方法,图4中鞋底形曲线范围内为被掩护攻击机的暴露区,因此友邻火力单元配置在此区域不受干扰压制。红色区域则为利用IGSO算法求解的火力单元受干扰威胁最小的最佳配置区,配置在该区域的友邻火力单元可最大程度避免远距离支援干扰机的压制并可同时攻击两个方向的来袭敌机。

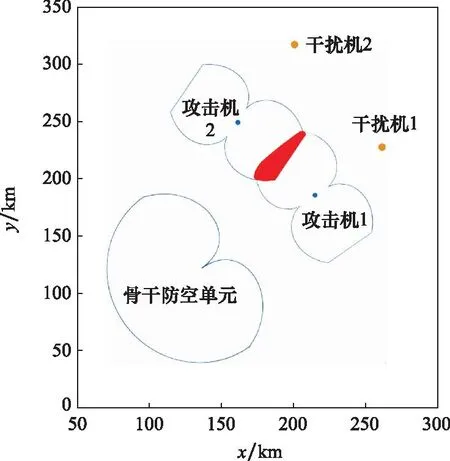
图11 仿真1的最佳可配置区结果图Fig.11 Simulation 1 of optimal configurable area result

假设在另外一次作战中,有两架敌方远距离支援干扰机从不同方向对我方骨干防空阵地进行干扰压制,干扰机1掩护一架攻击机,干扰机2掩护2架攻击机。两架干扰机的位置坐标分别为(161,346)、(253,244),飞行高度均为6 km,攻击机的坐标分别为(202,189)、(131,209)、(141,275),飞行高度为4 km,骨干防空火力单元的坐标为(85,80),两条突击方向分别被指挥员判定为主、佯攻方向,即方向1的权重λ1=0.2,方向2的权重λ2=0.8。干扰机参数和地面防空雷达参数与上次作战一致,仿真结果如图12所示。

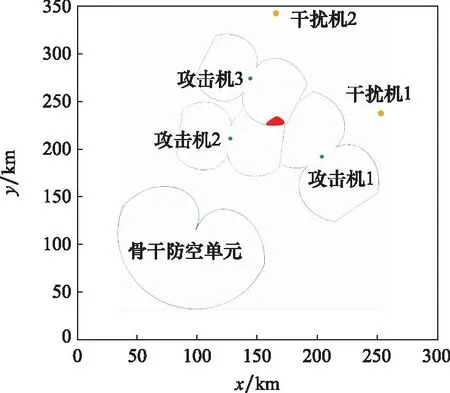
图12 仿真2的最佳可配置区结果图Fig.12 Simulation 2 of optimal configurable area result

可以看到,仿真图中红色的最佳配置区距攻击机3的距离是55.5 km,距离攻击机2的距离是37 km,而距离攻击机1的距离是61.6 km。这是由于λ2取值较大,则友邻火力单元配置区域需着重考虑抵御攻击机2和攻击机3,因此本次仿真最终选取的最佳可配置区域更加靠近方向2,同时也保证攻击机1在地空导弹的发射区近界以内。通过仿真可知,按照本文对在远距离支援干扰条件下地面防空兵力最佳配置区的建模能够满足实际作战要求,证明了该定量化数学模型是科学和有效的。

5 结 论

本文围绕远距离支援干扰“三点一线”战术运用模式所形成的目标暴露区,提出了一种地面防空兵力最佳配置规划算法。当干扰方向为一个时,一定能够找到地面防空兵力抗远距离支援干扰的最佳可配置区,但当干扰方向大于等于两个时,在特殊干扰角度情况下可能会发生无法同时应对多个干扰方向的最佳配置区情形,或者说多个干扰方向的地面防空兵力最佳配置区没有交集的情形,此时只能按照不同的干扰方向,分别规划地面防空兵力,从而形成非劣配置方案。