基于渐消因子的ECEF-GLS估计算法

董云龙, 张 焱,2,*

(1. 海军航空大学信息融合研究所, 山东 烟台 264001;2. 中国人民解放军32654部队, 山东 济南 250000)

0 引 言

多传感器数据处理系统中的各种误差是影响目标跟踪和数据融合质量的一个重要因素,而误差配准则是系统中的一个重要环节[1]。配准是对雷达等传感器系统偏差进行精确估计和补偿的过程,根据用于系统偏差估计的信源类型,可以将已有的误差配准工作分为有(准)合作目标条件下的雷达误差配准问题和无合作目标条件下多雷达组网误差配准问题。有(准)合作目标的误差校准技术利用准确的目标位置数据,如合作目标的全球定位系统(global positioning system, GPS)数据、自动相关监视-广播/自动识别系统(automatic dependent suveillance-broadcast/automatic indentification system, ADS-B/AIS)数据等,对雷达系统偏差进行标校[2-6]。

无合作目标条件下的误差配准技术是研究的重点,其实质是参数估计反演问题,即利用多部雷达对同一目标(位置未知)的协同观测数据,基于雷达与目标之间的空间几何关系对系统偏差进行精确解算估计与补偿[7]。最早关于雷达组网误差配准的研究成果是文献[8]给出的实时质量控制(real time quality control, RTQC)算法,后续许多雷达配准算法都是基于该算法的思路提出的。其中,文献[9]将地心地固(Earth-centered Earth-fixed, ECEF)坐标系引入协同探测模型,并利用最小二乘估计方法提出了基于ECEF坐标系的误差配准算法,较好地解决了远距离三坐标雷达误差配准问题。文献[10-11]在此基础上提出基于ECEF坐标系的广义最小二乘估计误差配准算法。但以上批处理的算法模型过于简单,虽更适用于工程,但随着雷达采样次数的增加,新的观测数据会对历史量测产生很大影响,若系统误差发生了突变,再用历史量测数据估计误差精度会大幅下降。针对系统偏差非恒定(时变)问题,提出基于滤波技术的实时误差配准算法。此类误差配准技术分为两类,一是单独构建系统偏差的观测模型,对系统偏差进行独立跟踪滤波[12];二是将系统偏差作为系统状态向量的组成部分,实现联合扩维滤波[13-14]。但以上实时配准的算法模型构造相对复杂,系统偏差配准易受机动目标的影响。

为有效解决上述问题,本文将渐消因子引入基于ECEF坐标系的广义最小二乘算法(generalized least squares algorithm based on the ECEF coordinate system, ECEF-GLS)中,对常规的ECEF-GLS进行修正,弱化历史量测对配准的影响,并给出了渐消因子合理的设计方法。仿真结果表明,在系统误差非恒定场景下,相较与常规算法,该算法获得了较好的性能改善,能对时变的系统偏差进行实时稳健估计。

1 ECEF-GLS配准算法

ECEF-GLS误差配准算法解决了远距离误差配准问题。当两部雷达相距较远时,将雷达为中心的局部东北天坐标转换到统一的ECEF坐标系中,利用“两部雷达在没有系统偏差和随机误差时,在ECEF坐标系中位置相同”这一空间几何关系,构造出伪量测、系统偏差之间的线性关系模型,进而运用广义最小二乘估计,实现系统偏差配准。

设定两部雷达协同观测场景为(LA,λA,HA)和(LB,λB,HB)分别为雷达A和B的地理坐标,(xAS,yAS,zAS)和(xBS,yBS,zBS)分别为雷达A和B的ECEF坐标,(xAl,yAl,zAl)和(xBl,yBl,zBl)为其对应的局部东北天坐标。

则

(1)

(2)

将以上局部东北天坐标转换到ECEF坐标系:

(3)

(4)

式中:TA和TB为雷达A和雷达B所对应的坐标变换矩阵[15-19]。

令

(5)

(6)

式中:

(7)

(8)

Y=Hβ+ξ

(9)

式中:

(10)

H=[G1,G2,…,Gk,…,GN]T

(11)

ξ=[F1∂φ1,F2∂φ2,…,Fk∂φk,…,FN∂φN]

(12)

N为配准量测个数,∂φk为两部雷达量测的随机误差向量。

(13)

根据式(9)所示线性关系,运用广义最小二乘估计可以得出雷达系统偏差的准确估计:

(14)

(15)

因为Σξ为3N×3N的分块矩阵{Σ1,Σ2,…,Σk,…,ΣN},所以式(14)和式(15)可以迭代计算:

(16)

(17)

2 基于渐消因子的ECEF-GLS

ECEF-GLS中假设雷达探测系统偏差不随时间变化,即一个与时间无关的恒定值。这一假设在系统偏差突变或缓变时,不再成立,因此历史时刻的量测会严重影响当前时刻系统偏差估计的准确性。针对这一问题,基于式(16)和式(17)可以迭代计算的特点,引入渐消因子,不断弱化历史量测的影响。

(18)

(19)

式中:ρ为渐消因子,0≤ρ≤1。

令

(20)

(21)

则

(22)

(23)

3 渐消因子设计方法

渐消因子决定了历史观测对系统偏差估计的影响,ρ越小,则历史观测对系统偏差估计的影响越弱,不同渐消因子在不同扫描周期对应的影响系数ρk变化情况如图1所示。

图1 不同渐消因子在不同扫描周期对应的影响系数ρk变化曲线Fig.1 Curve of influence coefficient ρk corresponding to different fading factors in different scanning periods

极端情况下,ρ=0时只能使用当前观测进行误差配准,此时当两部雷达协同观测点迹较少时,系统偏差估计精度严重恶化。反之,ρ=1时历史观测与当前时刻观测在配准算法中作用相等,算法退化为常规意义上的ECEF-GLS。

与上述两种极端情况类似,ρ选取的过大,则历史观测影响过大,算法时间灵敏度下降,对于快变的系统偏差,估计性能恶化。ρ选取的过小时,则历史观测影响过小,当两部雷达协同观测的目标数量较少时,就没有足够多的协同观测支撑误差配准的准确估计。

综上所述,ρ的选取由一个扫描周期(一帧)中两部雷达扫描协同观测个数n和雷达系统偏差变化快慢综合确定。

假定在系统偏差恒定条件下误差配准需要nmax个协同观测才能实现误差精确估计,每帧n个协同观测,则需要κ(nmax/n)个扫描周期,配准才能满足精度要求,其中κ(κ≥2)是考虑渐消因子影响而配置的放大系数。

设定ρk≤0.01时历史观测忽略不计,则可以得到渐消因子参数为

ρ≥10-2/(κ(nmax/n))

(24)

另一方面,设定雷达系统偏差快慢有关的时间灵敏度为TS,两部雷达中扫描周期最大值为Tmax,则ρ(Ts/Tmax)≤0.01,即

ρ≤10-2(Tmax/Ts)

(25)

若10-2(Tmax/Ts)≤10-2/(κ(nmax/n)),则得出结论现有协同量测数量不足以满足系统偏差配准时间灵敏度要求。反之,可在[10-2/(κ(nmax/n)),10-2(Tmax/Ts)]区间内选取任意值作为渐消因子。

若更关注配准精度则取值可以更靠近10-2(Ts/Tmax),若更适应系统偏差的时间灵敏度则选择更靠近10-2/(κ(nmax/n))的取值。折中方案可选取:

(26)

雷达系统偏差快慢有关的时间灵敏度TS一般根据经验值获取。在实际工程中,当系统偏差较大时,会对多传感器的关联效果造成影响。一种有效的办法是,当系统偏差超过某一门限时,多传感器航迹关联的错误率会显著提升,可以根据融合中心反馈的关联错误率反推系统偏差是否超过某一门限,通过统计雷达周期,推断雷达系统偏差变化的快慢程度。

4 仿真校验

实验 1假设两部雷达协同探测区域航迹数量为15,系统偏差在1 000扫描周期发生突变,其他条件同ECEF-GLS,采用常规的ECEF-GLS和本文提出的修正的ECEF-GLS(渐消因子合理)的跟踪效果。

图2～图7是常规算法和修正算法跟踪效果的比较。可以看出,当系统误差发生突变或快速变化时,常规的ECEF-GLS误差配准效果严重恶化;在渐消因子选取合理情况下,相较于常规算法,本文算法可实时有效估计系统偏差,并且跟踪速度快、配准性能好。

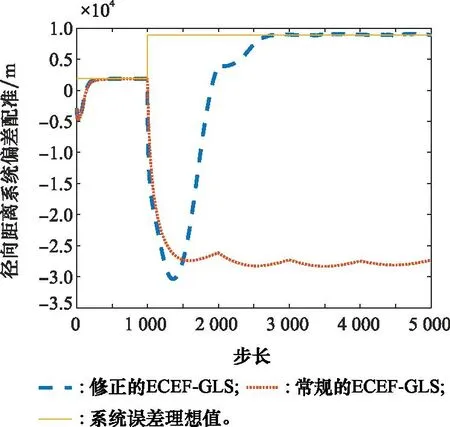
图2 雷达A距离系统偏差跟踪效果(实验1)Fig.2 Tracking effect of range system deviation of radar A (experiment 1)

图3 雷达A方位角系统偏差跟踪效果(实验1)Fig.3 Tracking effect of azimuth system deviation of radar A (experiment 1)

图4 雷达A俯仰角系统偏差跟踪效果(实验1)Fig.4 Tracking effect of pitching angle system deviation of radar A (experiment 1)

图5 雷达B距离系统偏差跟踪效果(实验1)Fig.5 Tracking effect of range system deviation of radar B (experiment 1)

图6 雷达B方位角系统偏差跟踪效果(实验1)Fig.6 Tracking effect of azimuth system deviation of radar B (experiment 1)

图7 雷达B俯仰角系统偏差跟踪效果(实验1)Fig.7 Tracking effect of pitching angle system deviation of radar B (experiment 1)

实验 2环境同上,选取较小渐消因子、较大渐消因子和合理的渐消因子(折中渐消因子)时的跟踪效果。

图8～图13是基于本文所提出的修正ECEF-GLS,当渐消因子取不同值时系统误差的配准效果比较。可以看出,ρ的取值对系统误差配准效果影响显著。当ρ选取的值过小时,历史观测对新数据的影响过小,配准曲线呈振荡趋势,无法完成误差的精确配准;当ρ选取的值过大时,历史观测影响系数过大,算法时间灵敏度下降,对于突变的系统偏差无法快速有效跟踪。因此,结合协同观测个数和雷达系统偏差变化的快慢程度来综合确定渐消因子大小尤为重要。

图8 雷达A距离系统偏差跟踪效果(实验2)Fig.8 Tracking effect of range system deviation of radar A (experiment 2)

图9 雷达A方位角系统偏差跟踪效果(实验2)Fig.9 Tracking effect of azimuth system deviation of radar A (experiment 2)

图10 雷达A俯仰角系统偏差跟踪效果(实验2)Fig.10 Tracking effect of pitching angle system deviation of radar A (experiment 2)

图11 雷达B距离系统偏差跟踪效果(实验2)Fig.11 Tracking effect of range system deviation of radar B (experiment 2)

图12 雷达B方位角系统偏差跟踪效果(实验2)Fig.12 Tracking effect of azimuth system deviation of radar B (experiment 2)

图13 雷达B俯仰角系统偏差跟踪效果(实验2)Fig.13 Tracking effect of pitching angle system deviation of radar B (experiment 2)

5 结 论

本文研究了系统偏差突变或快速变化时的系统误差精确估计问题,提出了基于渐消因子的ECEF-GLS,并对渐消因子的选取问题进行研究,结合两部雷达在一帧中扫描的协同观测个数和雷达系统偏差变化快慢这两个要素,给出了合理的设计方法。仿真结果表明,本文算法可对时变系统偏差进行稳健估计,并且跟踪速度快,更适合工程应用。