基于广义Rao检验的单/多比特MIMO雷达运动目标检测方法

黄广佳, 程 旭, 饶 彬, 王 伟

(中山大学电子与通信工程学院, 广东 深圳 518107)

0 引 言

近年来,计算机技术、信息通信技术的快速发展,催生出了多种运用新体制、新方法的现代雷达。Bliss等[1]在2003年将无线通信系统中的多输入多输出(multiple input multiple output, MIMO)技术引入雷达领域,最早提出了MIMO雷达的概念。目前,MIMO雷达主要分为两大类,一类为分布式MIMO雷达(非相关MIMO雷达),另一类为集中式MIMO雷达(相关MIMO雷达)。分布式MIMO雷达的收发天间相距较远,能够从不同视角观测目标,从而克服雷达截面积(radar cross section, RCS)闪烁效应[2],提高探测性能;集中式MIMO雷达通过运用波形分集等技术,提高系统设计的自由度,从而提升系统的整体性能[3],实现更好的角度估计、低信噪比(signal noise ratio, SNR)下的目标检测等。

大规模MIMO雷达需要同时处理来自多个接收通道的回波,这给其数据传输和处理能力带来巨大压力,尤其是随着雷达逐渐走向民用化、小型化,其规模、功耗、处理能力和传输带宽都受到了严苛的限制。比特量化技术能在牺牲一定信号完整性与检测性能的同时换取更低的处理负担与相同带宽下更高的采样率,以缓解雷达数据传输和处理的负担。单比特与多比特量化作为最理想与次理想的量化方式,近年来被广泛研究。例如:文献[2]提出了一种基于单比特量化的大规模MIMO雷达系统目标直接定位算法;文献[4]运用时变门限的单比特MIMO雷达在大幅减少数据量的情况下实现了高分辨率的参数估计;文献[5]提出基于极大似然的单比特MIMO雷达联合角度和多普勒频率估计方法;文献[6]就单比特MIMO雷达进行了性能分析,并运用交替方向乘子法(alternating direction method of multipliers, ADMM)求取了较优单比特波形;文献[7]研究了单比特调频连续波雷达的目标探测问题,并提出了一种两阶的目标检测方法;文献[8]设计了时变的量化阈值,对信号进行单比特采样与量化,并在文献[9]对单比特雷达的动目标参数进行了估计;文献[10]给出了单比特下集中式MIMO雷达的似然比检验;多比特量化雷达的研究,例如文献[11],对调相连续波雷达回波进行了多比特量化与参数估计;文献[12]分析了合成孔径雷达成像中多比特量化较单比特量化的增益。

目标检测是雷达系统的第一要务[13],也是后续任务的基础。众所周知,在参数未知条件下,常用的检验方法为广义似然比检验(generalized likelihood ratio test, GLRT),它使用未知参数的极大似然估计(maximum likelihood estimation, MLE)代替未知量本身,在实际中拥有良好的检测性能[13],但当未知参数的MLE没有闭合解时,GLRT需要对未知变量的MLE进行搜索,计算复杂度显著提高。幸运的是,在弱信号条件下,Rao检验方法可以避免对未知参数的MLE,因而备受青睐。例如,文献[14]和文献[15]分别研究了无线传感器网络(wireless sensor networks, WSNs)中未知参数的单比特和多比特量化的Rao检验问题;文献[16-17]将Rao检验应用场景拓展至未知运动目标的检测,针对WSNs中多比特量化非合作动目标去中心化检测问题,提出了广义Rao(generalized rao, G-Rao)检验统计方法;文献[18]利用G-Rao检验与局部最优检测解决了存在乘性衰落下WSNs对非合作目标的分布式检测问题;文献[19]设计了基于Rao检验与Wald检验的集中式MIMO雷达自适应检测器;文献[20]研究了集中式MIMO雷达的单比特量化方法,并分析了单比特量化对检测性能的影响,得出了低SNR下单比特量化Rao检测器相较于未量化GLRT的性能损失约为2 dB的结论;文献[21]研究了集中式MIMO雷达在多比特量化下的弱目标检测问题,发现3比特量化Rao检验方法在实现计算复杂度降低的同时,其检测性能已经接近未量化的GLRT。

本文研究集中式MIMO雷达的运动目标量化检测问题,该问题的关键点在于如何量化数据并进行检测,即如何选取量化位数、量化门限与检验统计量,以在保证目标检测性能水平的同时,降低对数据传输和计算复杂度的要求。主要工作包括:

(1) 建立集中式MIMO雷达运动目标检测场景并构建回波信号模型,每个接收天线均对回波信号进行量化,并将量化后的信号传输至融合中心(fusion center, FC)。由于在对运动目标进行建模时引入了冗余参数多普勒频率,此时经典的Rao检验方法不再适用[13],本文引入G-Rao检验方法[16-17]求解上述检测问题。

(2) 推导G-Rao检验统计量的检测性能与量化门限之间的对应关系,且将量化门限与时间解耦,实现量化门限的提前优化和计算。根据该关系,运用粒子群优化算法[22](particle swarm optimization algorithm, PSOA)求解最优量化门限。

(3) 利用数值仿真实验,分别从不同量化位数、量化门限选择方式等不同角度验证G-Rao方法的性能,并对比其与GLRT之间的性能差异。结果表明:低SNR条件下,运用PSOA优化量化门限能提高G-Rao检验的性能;在相同场景下,G-Rao检测性能随量化位数的增加而提升,其中3比特量化在有效降低信号传输量的同时,检测性能接近采用非量化(原始信号)方式的检测性能;相同量化位数的G-Rao检测性能与GLRT相当,但计算复杂度更低。

1 信号模型

如图1所示,考虑集中式MIMO雷达检测某未知匀速直线运动目标。雷达采用均匀线阵,包含Nt个发射天线与Nr个接收天线,相邻天线间距为d,发射信号波长为λ,远场目标与线阵垂直方向夹角为φ。雷达信号的发射-接收矩阵可以定义为

图1 集中式MIMO雷达探测场景示意图Fig.1 Colocated MIMO radar detection scenario schematic diagram

(1)

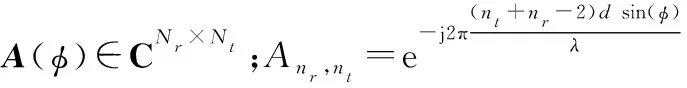
(2)

式中:l为采样时间序列,l∈{1,2,…,L}。

在短时间T内,不妨假定目标运动符合匀速直线模型,其相对集中式MIMO雷达的径向速度为v,则回波多普勒频率为fd=2v/λ,定义g(t,fd)exp(j2π(t-1)fdTr),其中Tr为脉冲重复间隔(pulse repetition interval, PRI),则信号在第t周期内,上述运动目标的MIMO雷达回波信号可以表示为

Mt=βg(t,fd)A(φ)S+N

(3)

(4)

(5)

式中:Uq(k)表示第k个接收通道使用q位量化器进行量化,q位量化的量化门限集可以表示为τk={τk(u),u=0,1,…,2q(k)}。在进行q位量化时,根据2q(k)+1个量化门限(始终有τk(0)=-∞,τk(2q(k))=+∞)将回波实部与虚部分别量化为2q(k)个离散值中的一个,即

(6)

(7)

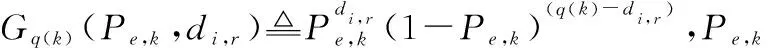
(8)

式中:ξ={β,fd}。

于是,FC收到T个脉冲周期的回波信号Y1:T的似然函数为

(9)

根据上述信号模型,构建目标检测的二元假设检验:

(10)

式中:t=1,2,…,T;l=1,2,…,L;k=1,2,…,Nr。

至此,本节构建了集中式MIMO雷达的运动目标回波模型和量化方法,下一节将基于量化结果,运用GLRT与G-Rao检验方法对目标进行检测。

2 检验统计量的推导

2.1 GLRT方法

由于式(9)含有未知检验参数β,且fd也未知,常用的GLRT方法要求用未知参数的MLE代替似然比检验中的待检测量[13],有

(11)

(12)

2.2 G-Rao方法

(13)

式中:FI(β)E{(∂lnP(Y1:T;ξ)/∂β)2}为Fisher信息矩阵。考虑β的实部与虚部在处理过程中的独立性,此处将G-Rao检验统计量改写为对β的实部与虚部分别求导的形式,即有

(14)

对似然函数(式(9))取对数,并对目标反射率β的实部求导,有

(15)

根据式(8)、式(9)有

(16)

(17)

对Fki(u)求一阶导、二阶导,分别有

(18)

(19)

(20)

同理,有

(21)

经推导,Fisher信息的显式表达式为

(22)

综上,将式(20)～式(22)代回式(15),即可得到问题的G-Rao检验的检验统计量为

(23)

2.3 复杂度分析

3 量化器设计与优化

3.1 量化器设计

已有文献[16]证明,G-Rao检测器的渐近检测性能与GLRT相同,均有

(24)

其中,

λQ(x1:T)(β1-β0)TFT(β0)(β1-β0)=

(25)

(26)

3.2 运用PSOA优化量化门限

对于式(26)的优化问题,采用PSOA[22]来优化量化门限,相较于模拟退火(simulated annealing, SA)[27]、遗传算法(genetic algorithm, GA)[28]等启发式算法与共轭梯度法(conjugate gradient method, CGM)[29]等基于梯度的优化算法,PSOA原理简单、所需调整的参数少、搜索速度快,能满足优化式(26)的需要。PSOA的基本原理不再赘述,这里描述其应用于本文量化门限确定的具体过程。

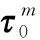
(27)

然后,开始迭代搜索,根据以下规则更新所有粒子的速度和位置:

(28)

(29)

上述PSOA描述为如下的算法1。

算法 1 PSOA输入 最大量化门限τmax, 量化位数q, 粒子数M, 终止速度vtol, 收敛因子ω,最大迭代次数itermax, 学习因子c1、c2, 高斯白噪声方差σ2n输出 最优位置(即量化门限向量)gbesti∈R1×(2q-1)1初始化迭代器i=0;2对 m=1,2,…,M 进行3在范围内随机初始化第m个粒子的位置(即门限向量)和速度;4根据式(26)计算该位置(门限向量)的Am(τm0),并将其位置初始化为粒子最佳位置pbestm0;5根据所有粒子初始化的pbest0得到初始全局最佳位置的gbest0;6重复7更新迭代器i=i+1;8对 m=1,2,…,M进行9根据式(27)更新粒子的位置τmi和速度vmi;10根据式(26)计算该位置(门限向量)的Am(τmi),并通过式(29)更新粒子最佳位置pbestmi;11根据所有粒子本次迭代的pbestmi得到当前全局最佳位置gbest0;12直至 i>itermax 或maxm=1,2,…,Mvmi≤vtol

4 数值仿真

4.1 均匀量化和PSOA优化量化的性能对比

表1 经PSOA优化量化的门限结果Table 1 Optimized quantization threshold by PSOA

图2 均匀门限与PSOA优化门限的G-Rao检验ROC曲线Fig.2 G-Rao test ROC curves for uniform threshold and PSOA optimization threshold

4.2 不同量化位数的性能对比

本节运用得到的优化量化门限,就同一场景下的接收信号分别采用q={1,2,3,4}位的量化并进行105次G-Rao检验蒙特卡罗仿真,得到各量化位数下的ROC曲线如图3所示。从图3可以看出, 2比特量化所带来的检测性能较1比特量化有显著提升,3比特量化较2比特量化的检测性能小幅提升,而4比特量化与3比特量化的检测性能相近。权衡检测性能与量化后所需的传输带宽与处理能力,3比特量化可谓折中的较优量化位数选择。

图3 不同量化位数下的G-Rao检验ROC曲线Fig.3 G-Rao test ROC curves at different quantization bits

4.3 G-Rao方法检测性能与SNR的关系

固定Pfa分别为10-4与10-3,G-Rao检验器的检测概率与SNR的关系图如图4所示。从图4可以看出,Pfa越小,相同SNR下Pd越低。此外,仿真得到的单比特量化Pd较3比特量化的检测性能损失约为2 dB,这与文献[20-21]所得出的结论相同。

图4 检测概率-SNR曲线(Pfa=10-3与Pfa=10-4)Fig.4 Detection probability-SNR curves (Pfa=10-3 &Pfa=10-4)

4.4 G-Rao检验与GLRT的性能对比

本节对G-Rao检验与GLRT方法在同一场景下进行105次蒙特卡罗仿真,得到的ROC曲线如图5所示。

图5 G-Rao检验与GLRT的ROC曲线Fig.5 ROC curves of G-Rao test and GLRT

从图5可以看出,在相同量化位数下,G-Rao与GLRT方法的ROC曲线基本重合。而当量化位数由3增加到4时,G-Rao方法的性能并没有进一步显著提升,这是由于,当q=3时,G-Rao、GLRT性能已经比较接近未量化的GLRT方法。

最后,对G-Rao与GLRT方法的计算量进行对比。本次研究采用的计算平台为搭载Xeon-4210R@2.4 GHz与64G RAM的Windows工作站,软件为Matlab R2021b,排除代码结构等因素对仿真耗时影响,各情况下105次蒙特卡罗仿真平均耗时见表2。由表2中的结果可以看出,GLRT对目标反射率β的幅值和相位的网格搜索会带来极大的运算量,这也凸显了G-Rao检验在计算量上的优越性,每多一个维度的搜索,其带来的计算量成倍增长。

表2 平均每次蒙特卡罗耗时Table 2 Average time per Monte Carlo

5 结束语

本文研究了集中式MIMO雷达在高斯白噪声下的非合作运动目标量化检测问题,建立了上述问题的数学模型,针对GLRT方法计算复杂度高的缺点,提出相应的G-Rao方法,给出了检验统计量的解析表达式。此外,本文还就量化门限的选取给出了目标函数,并运用PSOA得到了优化后的量化门限。最后的数值结果表明了本文模型、模型下的G-Rao检验与PSOA优化量化门限的有效性。在低SNR情况下,G-Rao检验的检测性能随量化位数的增加而提升,3比特量化的G-Rao检验性能已经接近未量化的GLRT,各量化位数下的G-Rao检验与GLRT检测性能相当,但G-Rao检验显著减少了计算复杂度,降低了数据传输与处理的负担,体现了G-Rao检验在计算复杂度上的优越性。

本文进一步的研究问题包括:① 在搜索未知参数时采用更优的策略来加快搜索速度,提高收敛能力;② 将模型进行拓展,使其能够适应不同的噪声特性;③ 推导更复杂的运动学模型下的G-Rao检验统计量;④ 研究分布式MIMO雷达模型下量化检测的相关问题等。