基于NSGA-Ⅲ的机载雷达空空射频隐身探测参数设计

刘 俊, 崔 宁, 谢佳昕, 行 坤

(1. 中国科学院空天信息创新研究院, 北京 100094;2. 中国科学院大学电子电气与通信工程学院, 北京 100049)

0 引 言

随着无源探测设备的广泛使用[1],机载雷达常需面临相比以往更加恶劣的隐蔽电磁环境,因此射频隐身能力成为被关注的热点问题之一。对于机载雷达而言,其首要任务是完成对目标的探测,但机载雷达在对外辐射功率进行探测的同时,也面临着被对方截获的风险。虽然可以通过在雷达参数设计[2]中降低辐射功率以实现低截获概率,但这又会使得机载雷达性能下降,不利于对目标的探测。因此,低截获概率机载雷达参数设计难点在于如何解决机载雷达射频功率有效使用与射频隐身之间的矛盾。

针对射频隐身的参数设计问题,国内外学者相继开展许多研究。文献[3]针对射频隐身搜索问题模型,通过非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)进行优化设计,以目标函数相乘的最小解为最优解,在维持较好检测概率的同时降低雷达辐射功率。文献[4]基于改进的粒子群多目标优化(multiple objectives with particle swarm optimization, MOPSO)算法实现线性阵列的功率分级,从而可根据待检测目标距离与雷达散射截面(radar cross section,RCS)的不同实现功率自适应调整。文献[5]建立目标跟踪过程截获风险模型,通过匈牙利算法实现低截获风险的调度方案设计。文献[6]考虑跟踪过程中的射频隐身问题,通过优化控制雷达探测过程中的辐射功率和发射间隔,来实现跟踪与射频隐身间平衡设计。文献[7]以截获概率最小化为目标函数,建立单次辐射能量控制模型,对雷达辐射功率与照射时间进行同时优化。文献[8]从最大信号不确定性角度出发,联合设计跳频周期与跳频间隔,并采用混合混沌粒子群优化算法,求解相应的最大条件熵模型,取得跳频周期与跳频间隔的自适应改变。文献[9]则考虑杂波背景下的射频隐身参数优化问题,基于截获因子建立相应的优化模型,通过遗传算法对辐射功率、脉冲积累数、驻留时间等参数进行优化。文献[10]以检测概率与截获概率为优化目标,建立双目标优化模型,并采用NSGA-Ⅱ算法求解。

然而上述方法主要是针对雷达常规工作模式设计,并未考虑机载雷达用于空中探测时目标场景特性,因此当用于机载雷达射频隐身探测参数设计时,无法取得满意的优化结果。本文针对上述问题提出一种新的机载雷达空中运动目标射频隐身探测模型。具体创新点如下:

(1) 与常见射频隐身模型不同,所提机载雷达空中动目标射频隐身探测模型联合检测概率、截获概率、雷达接收机信噪比、截获接收机信噪比形成四目标优化问题,同时考虑了空中目标运动特性,引入最大驻留时间作为约束条件,最终构成本文多目标优化问题;

(2) 先前射频隐身多目标优化问题研究常采用NSGA-Ⅱ求解,但该方法并不适用于三目标以上优化问题。针对此,本文结合近年新提出的用于多目标优化的NSGA-Ⅲ算法求解所提四目标优化问题模型。与采用NSGA-Ⅱ算法相比,所采用方法因为选择机制的改变,可以取得更优的Pareto最优解集;

(3) 与单目标优化问题不同,多目标优化问题所得结果为Pareto最优解集,因此后续还需对候选解集筛选以获得最终方案。然而先前研究所采用方法无法针对本文所得Pareto最优解集进行有效选取。据此,我们进一步结合层次分析(analytic hierarchy process,AHP)-逼近理想解排序法(technique for order preference by similarity to ideal solution,TOPSIS)形成本文的多属性决策选取策略,可以获得合适的最终解;

(4) 基于详尽的仿真实验对所提机载雷达空中运动目标射频隐身探测参数优化设计方法进行验证。

1 射频隐身探测优化模型

1.1 探测模型

空空探测中,机载雷达回波除包含目标信号外,还常充斥着严重的噪声干扰,因此机载雷达探测性能最直观的衡量标准就是信号与噪声功率之比,即信噪比[11]。更进一步,对于脉冲多普勒体制机载雷达而言,在进行门限目标检测前,往往需要对多个脉冲进行相干积累以提高其检测概率[12],所以检测概率作为另一较常使用的性能指标也广泛用于机载雷达设计中。其定义为在给定信噪比和虚警概率条件下,发现目标的概率。下面将结合上述两种指标对所提出空空射频隐身探测模型进行详细介绍。

经脉冲压缩和脉冲积累后的雷达方程可表示为

(1)

式中:R为雷达与目标径向距离;Pt为雷达发射功率;Gt代表发射天线增益;λ为雷达工作波长;σ表示目标的雷达散射截面积(radar cross section,RCS);D为脉冲压缩比;np为脉冲积累数,是驻留时间TD与脉冲重复频率fr的乘积;k为玻尔兹曼常数;T0为接收机噪声温度;Br为接收机带宽;Fn为接收机的噪声系数;Lr为综合损耗;SNR为雷达接收机信噪比。借由式(1),可求得SNR为

(2)

为计算检测概率,首先需要确定合适的RCS模型。经典RCS起伏模型有四种:Swerling Ⅰ、Ⅱ、Ⅲ和Ⅳ。通常情况下,由于存在模型失配影响,在实际设计中常选用较保守的Swerling Ⅰ模型进行指标估计。典型的Swerling Ⅰ型目标检测概率pd计算如下[13]:

(3)

pd=F(nfa,TD,SNR1)

(4)

式中:nfa代表虚警个数;特别地,当np>1时,nfa≈ln 2(np/pfa);TD=np/fr表示驻留时间。将nfa、TD代入式(3),可将式(4)进一步改写为

pd=F(R,σ,Pt,TD)

(5)

1.2 截获模型

在空空射频隐身探测中,除满足所需探测性能外,还应尽可能地避免被敌机截获,因此还需引入截获模型。截获模型用于评价射频隐身效果,常采用的指标有截获因子、截获概率等[14]。其中截获因子定义为截获距离与探测距离的比值,但并不适用于截获距离大于探测距离的情况,因此本文采用Lynch提出的截获概率作为隐身性能的评价指标[15],具体可表示为

(6)

式中:pi为截获概率;AF为天线波束的覆盖面积;DI为每平方公里截获接收机密度;TOT为雷达发射机对截获接收机照射时间;TI为截获接收机搜索时间;pF为发射机频率与截获接收机调谐到相同的概率;pD为在截获接收机在照射和调谐恰当的情况下检测到发射机波束能量的概率。

进一步,当pi≪1时,式(6)可以简化为

(7)

式中:MF为雷达主瓣波束覆盖区域面积;Pi为截获接收机接收功率;PI为截获接收机检测所需的功率;C0为覆盖面积与灵敏度的比例系数,本文采用圆形孔径典型值0.477。

通常情况下,截获机搜索时间TI大于发射机照射时间TOT,同时对截获机而言,为使每次被照射均有截获机会,最佳搜索策略是将其扫描时间与驻留时间匹配,即TOT=TD。综上所述,截获机发现雷达发射机位置的概率可近似表示为

(8)

将式(8)代入式(7)中,可得截获概率为

(9)

观察式(9)可知,为计算截获概率pi,还需求解参数MF与Pi。对于主瓣波束覆盖面积MF,本文采用“饼切”法估计。

如图1所示,假设天线方向图为圆对称,则径向距离R的横向分量Rc可表示为

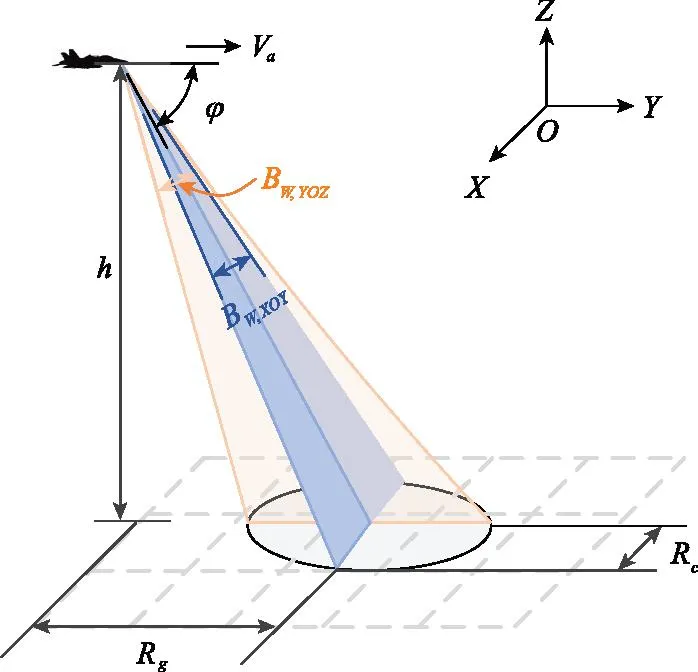
图1 主瓣波束覆盖面积示意图Fig.1 Schematic diagram of the area covered by the main flap beam

(10)

式中:Rg为波束覆盖纵向距离;BW,XOY为XOY平面内波束宽度。相应地,纵向距离Rg为

(11)

式中:h为载机与目标间的相对高度;φ为波束俯仰角。

对于YOZ和XOY方向而言,其最大波束宽度分别为

(12)

(13)

式中:U代表归一化sinθ区间内预定功率下降点处波束宽度,典型取值为1.6;a、b分别为天线孔径高度和宽度的一半。

将式(12)代入式(11)中,可得最大和最小的Rg分别为

(14)

当波束宽度较窄时,主瓣覆盖区域最大横向距离约为主瓣覆盖区域的纵向距离的一半,因此最大横向距离RL,max可近似为

(15)

根据式(12)～式(15),采用椭圆面积计算公式估计主瓣波束覆盖面积为

(16)

对于截获接收机的接收功率Pi求解,可根据截获机雷达方程,将Pi表示为

(17)

式中:GTI为雷达在截获机接收方向上天线增益;GIP为截获机处理器净增益;LI为雷达发射机与截获接收机之间损耗。则截获接收机信噪比SNRI可写为

(18)

式中:Ni为截获接收机的噪声功率;FI为截获接收机噪声系数;BI为截获接收机带宽。令截获接收机位于雷达主瓣波束内(GTI=Gt),将式(16)、式(17)代入式(9),得截获概率为

(19)

同样为表述方便,将式简写为

pi=G(R,σ,Pt,TD)

(20)

1.3 约束条件

在雷达空空探测设计过程中,应当令接收机的SNR大于给定阈值。根据式(1)可知,满足最小可检测信噪比Smin所需最小发射功率为

(21)

此外,还要考虑目标运动状态与距离分辨单元大小对驻留时间的影响。具体来说,对空中运动目标进行相干积累检测时,应尽可能避免产生距离单元走动,即波束驻留时间最大值应小于发生距离单元走动的最小时间[16]。如图2所示,假设载机运动速度为Va。当目标以速度Vt沿径向飞行于雷达主瓣波束内时,其停留时间可表示为

图2 空中运动目标状态示意图Fig.2 Schematic diagram of air moving target state

(22)

式中:ΔR=c/(2Br)为距离分辨率,其中c为光速,取值为3×108m/s。同样若目标以速度Va在主波束内沿切向飞行,则停留时间可写为

(23)

式中:Δθ为方位向上的主瓣宽度。一般而言Δta>Δtr,所以可认为单个波位的最大驻留时间满足

(24)

结合式(2)、式(5)、式(18)、式(20)、式(21)、式(24),空中运动目标射频隐身探测优化模型可描述为

(25)

2 模型求解

上节所提模型为四目标优化问题,并且四个优化目标之间存在冲突。因此这里采用多目标优化算法对该模型进行求解。目前,多目标优化求解方法大致分为两种:第一种是将多目标优化问题转化为单目标优化问题,然后再通过数学规划求解;第二种是采用多目标进化算法[17],如NSGA-Ⅱ[18]、SPEA2[19]、MOPSO[20]等进行求解。其中第一种方法每次只能得到某一权重下的最优解,且易受权值变化和目标次序影响,较不稳定。因此我们采用第二种方法,由于所求问题为四目标优化问题,而常用于射频隐身优化的NSGA-Ⅱ在此模型下求解性能不佳,所以本文引入由Deb等学者于近年提出的NSGA-Ⅱ算法[21],其为NSGA-Ⅱ的衍生方法,旨在解决涉及三个以上优化目标的问题。与NSGA-Ⅱ相比,NSGA-Ⅲ算法将采用拥挤距离进行选择操作改进为基于参考点的选择机制,有效地保持了多目标优化问题解的多样性,为实际应用中提供了多种选择方案。

此外,为取得最终设计方案还需对由NSGA-Ⅲ求得的Pareto最优解集进行筛选。实际应用中可通过多属性决策方法[22]实现上述目标。常见多属性决策方法有TOPSIS[23]、ELECTRE[24]、LINMAP等。其中,TOPSIS对Pareto最优解集的分布与数量要求较为宽松,计算结构易于实现。因此,本文结合TOPSIS进行多属性决策,同时通过AHP法[25]确定各属性的权重值。

综上所述,本文采用NSGA-Ⅲ算法对模型求解,获得Pareto最优解集后通过AHP-TOPSIS法确定最优折衷方案。利用AHP法确定Pareto解集各属性权重,利用TOPSIS法计算各方案与理想解和负理想解距离。算法流程如图3所示。

图3 NSGA-Ⅲ与AHP-TOPSIS流程图Fig.3 Flow chart of NSGA-Ⅲ and AHP-TOPSIS

具体步骤如下所述。

步骤 1设定NAGA-Ⅲ参数,输入式中的4个优化目标函数及发射功率Pi与驻留时间TD的取值范围。

步骤 2根据文献[21]的方法生成参考点。

步骤 3计算种群中每个个体的适应度。

步骤 4通过选择、交叉和变异生成子代种群。

步骤 5将父代种群和子代种群合并得到新的种群。

步骤 6对合并种群进行非支配排序并且基于参考点的选择操作,选择进入下一代的个体。

步骤 7重复步骤2～步骤6直至达到最大迭代次数,输出机载雷达空中运动目标射频隐身探测模型的Pareto最优解集。

步骤 8将截获概率、截获接收机信噪比这两个指标各自的最大值减去Pareto最优解集中的相应解,把所有指标统一为极大型指标以实现正向化。并且将正向化矩阵标准化,以免4个指标的量纲对结果产生影响。假设正向化矩阵记为Y=(yij)m×4,则标准化矩阵Z=(zij)m×4为

(26)

步骤 9构造判断矩阵A。对截获概率、检测概率、截获接收机信噪比、雷达接收机信噪比四个优化目标两两分析,用1～9标度法[26]对其重要程度进行判断,得到判断矩阵取值为

(27)

步骤 10通过计算式的最大特征值λmax,计算一致性指标CI与一致性比率CR

(28)

式中:判断矩阵维度n=4;平均随机一致性指标RI=0.9。当CR<0.1时,认为判断矩阵通过一致性检验,将判断矩阵最大特征值所对应的特征向量归一化,得到权值wj。假设加权标准化矩阵记为V=(vij)m×4,则

vij=wjzij,i=1,2,…,m;j=1,2,3,4

(29)

当CR≥0.1时,则重新构造判断矩阵A。

步骤 11计算相对逼近度,首先确定理想解与负理想解

(30)

(31)

式中:J+为效益型属性集;J-为成本型属性集。然后计算各方案到理想解和负理想解的距离

(32)

(33)

由此得到计算各方案的相对逼近度为

(34)

步骤 12选择相对逼近度最高的方案所对应的Pareto解作为最终结果。

接下来,将对上述求解方法的算法复杂度进行分析。为简化分析过程,这里以运算次数作为复杂度的评价指标。根据文献[21,27]可知,所提方法中占据主要计算开销的步骤为NSGA-Ⅲ中的非支配排序和种群关联至参考点操作,其复杂度可表示为max{O(N2logM-2N),O(MNH)},其中M为优化目标数,种群大小为2N,H为参考点数。实际应用中,常令H≈N和N≫M,则上述复杂度可简化为O(N2M)[28]。时间复杂度分析结果表明,种群数N对运算速度的影响要远大于优化目标数M。换而言之,如果种群规模设置过大,则计算开销会急剧增加;但若将种群规模设置过小,则易使结果陷入局部最优,因此应根据实际需求合理设置种群大小。

3 仿真与分析

本节基于仿真实验对所提机载雷达空空射频隐身探测参数设计方法进行验证,具体雷达参数、截获接收机参数和载机与目标的运动参数设置如表1～表3所示。实验过程中,NSGA-Ⅲ算法采用PlatEMO平台[29]实现。

表1 雷达参数Table 1 Radar parameters

表2 截获接收机参数表Table 2 Interceptor Receiver Parameter Table

表3 载机与目标的运动参数Table 3 Carrier and target motion parameters

3.1 算法有效性分析

本节实验将对模型的有效性进行验证。为便于实验对比,将目标RCS和R固定为3 m2和为70 km。为确定合适的NSGA-Ⅲ算法参数,引入超体积(hyper volume, HV)[30]作为评价指标[31]。如图4所示,为种群大小500条件下,基于蒙特卡罗方法得到的HV值与迭代次数的结果。从图中可以看出当迭代次数超过30次时,HV取值开始趋于稳定。结合上述结果,这里将迭代次数设置为100次以确保满足收敛要求。在此条件下,NSGA-Ⅲ算法的最大评价次数为50 000。其余参数如表1至表3所示。认为当检测概率大于0.9时满足探测需求,在此基础上截获概率应尽可能地小。

图4 迭代次数与HV值关系图Fig.4 HV vs. number of iterations

图5给出了基于NSGA-Ⅲ算法对上述模型求解所得的Pareto最优解集,共包含455个决策方案,其中SNRI取值与颜色表对应。图中红色标记为采用AHP-TOPSIS排序后,选择的相对最优决策方案,具体优化参数结果列于表4。表明对于RCS为3 m2,距离为70 km的空中运动目标的检测概率大于0.9,截获概率为0.035,能够实现在对目标进行探测的时候实现射频隐身。

表4 目标值与决策值Table 4 Objective and decision values

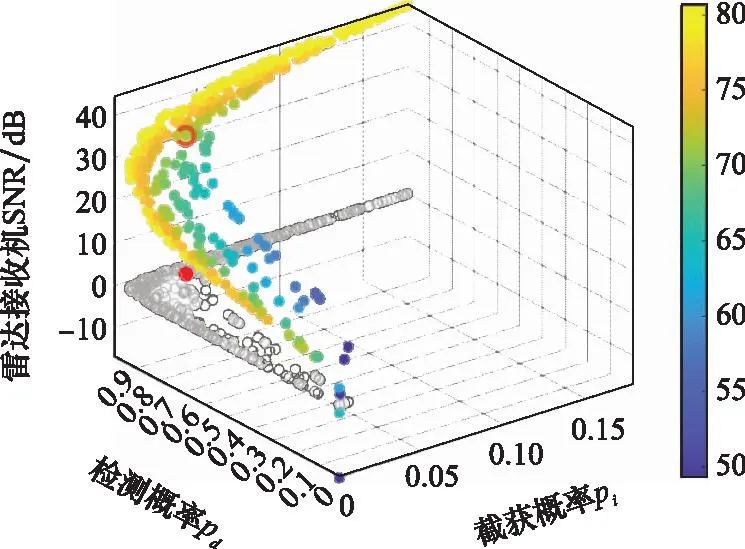
图5 Pareto最优解集与AHP-TOPSIS决策结果Fig.5 Pareto optimal solution set and AHP-TOPSIS decision results

3.2 不同距离对比

本节将对不同距离的目标优化结果进行对比分析。同样目标RCS设置为3 m2,其余参数设置同上。经AHP-TOPSIS法挑选后的结果如表5所示。当探测距离由20 km增加到80 km时,为满足检测需求,发射功率Pt也相应地从38.86 W提升至11 252.14 W,但这又会导致被敌机截获概率pi增加,因此需要减少脉冲积累数np以满足平衡。上述结果表明,所提方法可在约束条件内,平衡各参数指标并有效求解最优参数设计方案。

表5 不同距离下的优化结果Table 5 Optimization results at different distances

3.3 不同RCS对比

本节实验比较在相同探测距离下,目标RCS变化对射频隐身探测的影响。实验中探测距离为70 km,其余参数设置同前,所得优化结果如表6所示。从表6中数据可知,随着RCS增加,可以发现在优化过程中,通过增加脉冲积累数来减缓发射功率的提升,以保证在足够高的检测概率条件下实现射频隐身。上述结果进一步表明,所提方法可在给定参数区间进行最优决策,取得相对较优的设计方案。

表6 不同RCS下的优化结果Table 6 Optimization results with different RCS

4 结 论

本文针对机载雷达对空中运动目标射频隐身探测的问题,将检测概率、截获概率以及信噪比综合考虑,建立空中射频隐身探测多目标优化模型。并通过NSGA-Ⅲ对上述多目标问题求解,采用AHP-TOPSIS法挑选出相对逼近度最高的决策方案。数值仿真实验结果表明所提方法可在给定的参数区间内进行指标权衡设计,并从中挑选出最优折衷方案,可用于空中运动目标射频隐身探测应用。