无需先验测量误差的定位节点选择方法

汤建龙, 解佳龙, 陈弘凯

(西安电子科技大学电子工程学院, 陕西 西安 710071)

0 引 言

无源定位技术因只接收外来的辐射信号,本身不需要发射电磁信号,具有良好的安全隐蔽性等优点,受到各国学者的广泛关注[1]。无源定位技术已广泛应用于无人机、分布式传感器网络、卫星导航、外辐射源定位等领域[2-5]。无源雷达定位技术主要利用到达时间(time of arrival, TOA)、到达时差(time difference of arrival, TDOA)、到达频差(frequency difference of arrival, FDOA)、到达角度(angle of arrival, AOA),以及联合其中2～3种的定位体制对目标参数进行估计[6-10]。

在多传感器分布式定位中,对定位节点选择可以提高能量利用率、减少信息冗余[11],如何根据当前状态选择最优定位节点成为众多学者所思考的问题。通常情况下,节点选择问题可以描述为带有约束条件的最优化问题[12]。文献[13]将Fisher信息的最大化问题作为待求目标函数选择,利用穷尽搜索思想寻找最优定位节点子集。然而,随着站个数的增加,实际系统不可能应用高复杂度的方法。在线性估计模型的框架下,文献[14]对节点选择问题引入一组布尔量进行选择,同时将布尔约束条件进行凸松弛,使用内点法对问题进行求解,得到一组接近全局最优的次优解。文献[15]将节点选择问题使用稀疏促进思想,对布尔向量的基数作为稀疏促进惩罚项添加到代价函数中,实现了对多目标优化的节点选择。文献[16]研究了在TDOA与TDOA-AOA联合的无源定位系统中最优定位节点组合方法,通过将传统加权算法的协方差矩阵作为目标参数,通过凸优化方法进行求解。另外,贪婪算法在解决节点选择问题得到了广泛应用,在线性模型下,文献[17]提出一种随机贪婪算法的节点选择优化问题,在每个时间节点求最小化估计均方根误差(root mean square error, RMSE)。针对非线性估计模型,文献[18]中将智能优化算法引入到选星过程中,利用灰狼优化算法实现了多全球卫星导航系统组合导航选星。然而上述文献定位节点优选算法均需要获取先验测量误差的方差。

文献[19]与文献[20]提出一种不需要先验测量误差方差的目标定位算法,本文将该思路引入到节点优选问题中。利用TDOA-FDOA测量信息建立定位方程后,以现有两步加权最小二乘算法(two stage weighted least squares, TSWLS)目标定位误差的协方差作为目标函数,利用半定规划(semi-definite programming, SDP)算法来消去目标函数中包含的先验测量误差项。

其次,引入一组布尔向量对节点进行筛选,将这组布尔向量进行扩展,以选择节点数目作为约束条件,对目标函数与约束条件利用半定松弛技术(semi-definite relaxation, SDR),将非凸约束条件凸松弛,最终利用求得的节点选择结果对定位性能评估。仿真结果显示,本文所提的节点选择方法的定位精度与穷举搜索法相近,并且算法实时性高。

1 定位场景

(1)

不失一般性地,将s1设置为参考节点,第i个定位节点与参考节点之间的真实距离差和距离差变化率可以表示为

(2)

真实情况下,测量误差由多种因素造成,考虑测量误差时表示为

(3)

Qα=σ2Hα=blkdiag(Qt,Qf)

式中:σ2表示测量噪声的方差;Hα=blkdiag(R,γR)为总测量误差的结构矩阵;R为主对角线为1,其他元素为0.5的结构矩阵。本文假设Qf与Qt间噪声方差存在一个已知常数关系γ。

2 节点优选方法

2.1 目标函数构建

在现有节点优选的研究文献中,目标函数有不同的选择,包括克拉美罗下界(Cramer-Rao low bound, CRLB)最小原则[21-22]、互信息量准则[23]、估计误差的协方差最小原则[24]等。其中估计误差协方差最小原则作定位目标函数有定位效果好、算法误差小等特点,本文选择该原则为节点选择目标函数。

文献[25]给出了TSWLS算法估计误差协方差,具体如下所示:

(4)

式中:

(5)

式中:On×m表示n行m列的零矩阵;0n×1表示n维零向量。

将M个定位节点中接收功率最大的节点设为参考节点[26],在视距传播环境下,目标离观测节点越近,观测节点接收信号功率越大[24]。在参考节点确定后,观察式(4)和式(5),算法定位精度仅与TSWLS算法第1步中估计误差的协方差有关,协方差如下:

(6)

其中:

(7)

(8)

至此,确定了以式(6)为节点选择问题的目标函数,如何从剩余M-1个定位节点中选出最优的k-1个节点成为下一步工作的核心。引入一个布尔向量来实现该目标,布尔向量[27]表示为

z=[z1,z2,…,zM-1]T,zi∈{0,1}M-1

(9)

根据测量得到的TDOA-FDOA信息,对式(9)中的布尔向量扩展为l=[zT,zT]T。定义矩阵Φz为布尔向量l的衍生矩阵,用来筛选定位节点的信息,它与布尔向量l的关系表示为

(10)

在筛选节点后,定位目标参数的协方差矩阵的逆:

(11)

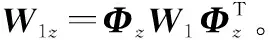
利用文献[28]中的A-optimality模型来构建目标函数,节点选择优化问题可以表述为以下形式:

(12)

对式(12)中的布尔向量约束条件进行凸松弛,并且引入辅助矩阵Y,其中Y=J-1,将上述问题化为如下SDP问题:

(13)

式中：符号 _ 表示半正定。

2.2 不需要测量误差的方法

构建节点选择目标函数的关键是获取节点选择目标函数式(6)中的加权矩阵W1,加权矩阵W1中包含有待求解目标的参数信息与先验误差信息。一般做法是先将加权矩阵W1设置为单位阵,然后利用最小二乘法求得初始值再迭代更新加权矩阵。本文对文献[25]中组成的TDOA-FDOA伪线性方程利用SDP算法进行目标初始位置求解,这一方法不需要先验测量误差。以下给出求解过程。

(14)

(15)

式中:

(16)

(17)

式中:

(18)

(19)

(20)

由于该优化方法中对布尔向量进行松弛,所得解为小数向量l=[zT,zT]T,而不是布尔向量,最直接的方法是选择向量l的子向量z中最大k-1个元素为1,z中剩余元素为0构成布尔向量用于节点筛选。

具体的节点优选算法步骤如下。

步骤 1将M个定位节点按接收功率大小排序,设置接收功率最大的节点为参考节点,从剩余M-1个定位节点中随机选择k-1个定位节点,建立k节点的TDOA-FDOA伪线性方程。

步骤 4根据得到的目标估计解利用式(6)建立M个定位节点的估计误差协方差。

步骤 5将步骤4得到的估计误差协方差作为节点优化目标函数,将目标函数中含先验测量误差项的加权矩阵利用最小问题等价思想替换为不含先验测量误差的矩阵结构。引入一组布尔向量z=[z1,z2,…,zM-1]T,zi∈{0,1}M-1,并将该布尔向量扩展成l=[zT,zT]T,用来对误差协方差中对应的节点进行筛选,构建无需先验测量误差的节点优选方程,如式(20)所示。

步骤 6经求解式(20)得到一组小数向量l,l的子向量z中最大k-1元素对应的节点确定最优节点。

步骤 7将步骤6确定的最优节点代入闭式解算法评估节点定位性能。

3 复杂度分析

表1给出了从25个定位节点选择k个节点(k分别为4、6、8、10)情况下穷尽搜索算法与本文算法的运行时间。从表1中可以看到,本文算法运行时间与定位站选择个数无关,并且算法运行时间短。

表1 算法运行时间比较Table 1 Algorithm run time comparison s

4 仿真实验

本节设计了3种仿真实验。实验1与实验2仿真研究了在25个定位节点个数下,选择不同参与定位站个数,在随测量误差变化时,不同节点选择算法对目标参数估计性能对比。实验3研究了对运动目标持续观测下,不同节点选择结果对目标的位置以及速度的估计性能比较。

对比方法包括最近距离法、穷尽搜索法以及随机选择法,采用估计RMSE对各算法的定位性能进行衡量,其定义式为

(21)

4.1 实验1

考虑从25个定位节点中选择k=6个节点参与定位,定位节点与目标均随机分布,其中定位节点的位置坐标服从0均值,标准差为3 000 m的高斯分布,目标位置坐标服从0均值,标准差为1 000 m的高斯分布[30];定位节点速度与目标速度均服从0均值,标准差为100 m/s的高斯分布。

图1给出了当测量误差为-10 dB时不同节点选择方法选择出的节点序号,从图1中可以看到,穷尽搜索法选择的定位节点是(1,4,9, 10,14,23),本文算法按照选择权值从大到小选择最大的k个节点也是(1,4,9,10,14,23)号节点,所提算法选择了与穷尽搜索法相同的定位节点。

图1 k=6时不同算法选择的定位节点序号Fig.1 Number of positioning nodes selected by different algorithms when k=6

图2给出了测量噪声强度从-10 dB到10 dB变化时,不同节点选择方法对定位时的估计性能影响。从图2中可以看到,本文所提算法能够达到穷尽搜索的定位精度,相比于随机选择法与最近距离法具有更优的定位性能。随机选择节点因为站的选择未考虑具体情况,使得在相同定位算法下定位效果出现定位性能不稳定的情况。在测量误差达到10 dB时本文算法的定位性能与穷尽搜索法定位效果相同,对目标位置误差优于最近距离法1 m以上,对目标速度误差优于最近距离法0.5 m/s以上。

图2 不同测量噪声条件下的6定位站RMSEFig.2 RMSE of six positioning stations under different measurement noise conditions

4.2 实验2

考虑从25个定位节点中选择k=12个节点参与定位,定位节点参数与目标参数同实验1设置,均为随机产生的一组定位节点与待测目标。

图3给出了当测量误差为-10 dB时不同节点选择方法选择出的节点序号,从图3中可以看到,从25个定位节点选择的12个节点结果下,本文算法与穷尽搜索法选择的定位仅有1个选择节点不同。从图4的定位性能图中可以看到,所提方法能够达到穷尽搜索一样的定位效果,并且本文所提算法不论是对目标位置或速度的估计都要优于最近距离法与随机选择法。从侧面反应了在不同测量噪声下,本文算法的节点选择结果与穷尽搜索法的节点选择结果相似。

图3 k=12时不同算法选择的定位节点序号Fig.3 Number of positioning nodes selected by different algorithms when k=12

图4 不同测量噪声条件下的12定位站RMSEFig.4 RMSE of 12 positioning stations under different measurement noise conditions

实验1与实验2均为在某一时刻下,对目标在不同测量误差下的节点选择定位性能比较,并且对于布站范围与目标设置区域有着局限性,即目标均在定位节点范围内,这点在实际应用中有很强的局限性。因此本文设计了实验3场景来对本文算法做进一步验证。

4.3 实验3

图5 仿真场景分布图Fig.5 Simulation scene distribution diagram

图6给出了观测时间内不同定位节点算法的估计性能,从图中可以看到随着目标由远到近移动,本文所提算法的定位性能十分接近穷举法的定位性能。同时,还可以看到最近距离法在目标接近观测站才有较好的定位性能,随机法的定位性能表现不稳定,通过该仿真实验进一步说明节点选择的重要性以及本文所提方法的有效性。

图6 不同观测时间内节点选择算法估计性能对比Fig.6 Comparison of estimation performance of station selection algorithms at different observation times

5 结 论

本文在现有节点选择研究的基础上,提出一种新的不需要先验测量误差的时频差节点选择方法。与现有方法相比,所提方法在不需要先验测量误差量,并且在定位性能上非常接近穷尽搜索算法。同时,由于考虑了目标速度因素,在定位节点选择上对运动目标能够实现更好的定位效果。相比于穷尽搜索算法,所提方法复杂度低、实时性好。仿真验证了在不同测试环境下所提方法的有效性。