基于检测-跟踪算法的多分量瞬时频率-调频率估计

卢 杰, 张文鹏, 刘永祥, 杨 威

(国防科技大学电子科学学院, 湖南 长沙 410000)

0 引 言

非平稳信号广泛应用于雷达信号处理[1]、生物医学[2]、无线通信[3]等领域。对于非平稳信号,常用的表征方法包括时域分析、频域分析、时频联合分析。作为非平稳信号的重要特征,瞬时频率(instantaneous frequency, IF)和瞬时调频率(instantaneous frequency rate, IFR)在分析具有多分量的非平稳信号时极具潜力。通过对瞬时频率和瞬时调频率进行联合分析[4-6],有望对非平稳信号进行更为有效表征。

瞬时频率估计一直是非平稳信号处理领域研究的热点问题,现有瞬时频率估计方法可分为参数方法和非参数方法两大类,主要基于信号的时频分布实现。相比于单一的时域分析或频域分析,时频分析可以表征信号瞬时频率随时间的变化趋势[7],常用的时频表征包括短时傅里叶变换(short time Fourier transform, STFT)、小波变换、魏格纳分布、S变换等。参数方法往往通过预设信号数学模型,通过估计模型参数从而获取实现瞬时频率估计,其典型方法包括霍夫变换[8]、拉东变换[9]、逆拉东变换[10]等。参数方法对于瞬时频率估计有着优异的性能,但预设的信号模型难以应用于实际场景中复杂的信号形式。非参数方法首先需要获取信号时频分布。单分量信号在时频分布中表现为能量集中的脊线,通过谱峰提取[11]、维特比算法(Viterbi algorithm, VA)[12]、脊检测算法[13]可以进行有效提取。多分量信号曲线在时频域存在交叉、重叠,难以区分。为应对该问题脊线跟踪算法[14]、岭迹重组算法[15]、改进维特比算法[16]等相继提出,在一定程度上解决了分量关联问题,但仍然存在计算量大、易受信噪比影响等问题。

当求得瞬时频率后,通过求导可以获得瞬时调频率,但容易产生误差传递,因此众多学者直接针对瞬时调频率开展研究。作为最为常见的非平稳信号,线性调频信号(linear frequency modulation signal, LFMS)是一种二阶多项式相位信号(polynomial phase signal, PPS),其瞬时频率随着时间线性变化。众多学者以研究LFMS为基础,开展了一系列对更高阶、更复杂信号的研究。基于最大似然估计[17]及基于分数阶傅里叶变换[18]的算法性能优良且估计精确,但该方法计算量大,且仅适用于LFMS。三次相位函数(cubic phase function, CPF)是针对三阶PPS信号的检测与参数估计提出的一种非线性变换方法[19],该方法性能优异但对于高阶PPS信号误差较大,且对于多分量信号存在严重交叉项干扰。基于CPF的改进算法[20-21]可以对交叉项进行抑制,但往往会抑制信号中的弱分量。对于高阶PPS信号,基于高阶模糊函数(high-order ambiguity function, HAF)的估计方法[22]通过递归计算估计多项式相位系数实现瞬时调频率估计,HAF与CPF同为非线性变化,因而也会受到交叉项的干扰,且当PPS信号的阶数过高或者低信噪比时,其估计性能将严重下降。

近年来,基于时间-频率-调频率(time-frequency-frequency rate, TFFR)的三维表征在非平稳信号分析中展现出重要作用[4-6,23],在时频平面存在交叉、难以区分的多分量信号在三维空间中不同分量发生交叠的可能性大幅降低,同时由于表征字典的精度提升,在该空间中能够实现更鲁棒、更准确的估计。文献[5]提出基于改进的匹配追踪算法对分量进行序贯提取,但需以分量数作为先验信息。文献[4]通过频率-调频率重分配方法提高了时间-频率-调频率三维表征的聚集度,通过三维脊检测方法分离各分量。而这些方法都将分量视作序贯求解过程。本文将该问题视作多目标检测-跟踪问题,提出基于检测-跟踪的多分量瞬时频率-瞬时调频率估计算法。首先对信号计算短时调频傅里叶变换(short time chirp Fourier transform, STCFT)获得三维TFFR表征,将时间-频率-调频率分布中的信号分量视为具有时序变化频率-调频率属性的多目标,由此通过改进的YOLOX检测器对每一时刻频率-调频率表征(frequency-frequency rate representation, FFRR)进行检测,由此获得每一时刻瞬时频率-调频率的估计和瞬时形状特征的提取。将每一时刻检测得到瞬时估计值和瞬时形状特征用卡尔曼滤波[24]进行关联获得瞬时频率-瞬时调频率随时间变化的三维曲线,由此实现对瞬时频率-瞬时调频率的联合估计。

1 时间-频率-调频率表征

本文主要研究时序上具有连续性的多分量非平稳信号,其一般表达式为

(1)

式中:Ai(t)和φi(t)分别为第i个信号分量的幅值和相位。则该分量瞬时频率和瞬时调频率可分别表示为

(2)

(3)

为分析频率特征不稳定的非平稳信号,STFT通过对加窗的信号片段进行傅里叶变换实现对信号频率的时变特性进行分析,其表达式为

(4)

式中:px(τ;t)为对信号x(τ)在t时刻加窗后所取信号片段,具体可写为

(5)

式中:lw为窗长。对于非平稳信号,STFT将加窗后的信号片段视为平稳信号进行分析,但固定窗长难以满足存在剧烈变化的信号时频分辨率的需求,且对于在时频域存在交叠的多分量信号难以区分。在STFT基础上,STCFT通过三维空间对多分量信号进行表征可有效区分多分量信号。为此,对于信号片段px(τ;t)可采用LFM信号对px(τ;t)中分量进行表征[5],即

(6)

式中:sk(τ)为中心频率为fk、调频率为βk的LFM信号,sk(τ)=exp(j2πfkτ+jπβkτ2);ak为信号幅度;e(τ)为误差项;J为信号分量数。为表征信号片段的瞬时频率和瞬时调频率,对每一个所得信号片段施加线性调频傅里叶变换,由此可得信号x(t)的短时线性调频傅里叶变换,其定义为

(7)

由此可获得信号x(t)的三维时间-频率-调频率表征。对于一个三分量信号,其FFRR如图1所示。

图1 FFRR图Fig.1 FFRR diagram

三维时间-频率-调频率表征中,任一时刻的二维FFRR平面会出现对应用于表征该信号片段的LFMS的峰值。其FFRR平面最大值可由式(8)求得

(8)

式中:f0和β0分别为表征该信号片段的LFMS的瞬时频率和瞬时调频率。对于单分量信号,通过式(8)基本可以实现对于信号的瞬时频率和瞬时调频率的估计,但并不适用于多分量、存在散焦模糊情况的复杂情况。

窗长的选取是影响二维FFRR的关键因素,窗长设置过小,易导致频率-调频率域分辨率低,而窗长设置过大往往导致表征不够准确,对于高阶信号表征存在较大误差[4]。图2展现了不同窗长对正弦调频信号(sinusoidal frequency modulated signal, SFMS)和LFMS的FFRR表征的影响。随着窗长增大,LFMS在FFRR平面聚集程度更高,而SFMS在窗长较大时其非线性现象更显著,此时调频傅里叶变换存在表征偏差逐渐出现畸变和扩散。

图2 FFRR受窗长影响Fig.2 Effect of window length on FFRR

频率分辨率和调频率分辨率与FFRR的聚焦程度密切相关,为两个维度剖面的主瓣宽度,因而也受到窗长的影响。设窗长为Nwin,采样频率为fs,频率的理论分辨率可由fs/Nwin计算,因此频率分辨率随窗长增大而减小。调频率分辨率与窗长之间的关系更为复杂,在一定范围内随窗长增大其主瓣宽度减小,分辨率减小。但窗长过大会引起高阶非线性相位信号主瓣的扩散,甚至会出现多峰,对应FFRR出现变形,如图3所示。图3中,黑色虚线对应-3 dB,通过计算信号主瓣在-3 dB处坐标位置差值可以获得分辨率;当Nwin=115时,LFMS调频率分辨率为102 Hz/s,SFMS调频率分辨率为111.9 Hz/s。

图3 不同窗长下LFMS和SFMS调频率剖面Fig.3 Frequency rate profile of LFMS and SFMS with different window length

设STCFT采用长度为Nwin的矩形窗,对加窗信号进行NFFT点傅里叶变换,则任一时刻所生成二维FFRR长宽均为NFFT。二维FFRR的频率采样间隔Δf和调频率采样间隔Δfr分别为

(9)

(10)

2 基于检测-跟踪的瞬时频率-瞬时调频率估计方法

经过STCFT变换后,信号在频率-调频率域中对应频率和调频率位置会产生显著特征区域,通过对特征区域进行检测实现对瞬时频率、瞬时调频率进行估计。由于所生成特征区域具有峰值和形状特征,本文将所生成峰值所在特征区域视作待检目标,其随着时间的变化可以视作运动轨迹,由此将瞬时频率-瞬时调频率估计问题转换为多目标检测-跟踪问题。首先通过对二维频率-调频率平面进行检测得到峰值区域,通过卡尔曼滤波实现轨迹预测,将当前时刻检测峰值区域与上一时刻峰值区域进行时序关联,由此实现多分量IF-IFR估计,整体流程如图4所示。

图4 所提算法总体流程Fig.4 Overall flow chart of the proposed algorithm

2.1 基于检测的瞬时参数估计

信号经STCFT变换后会在FFRR平面出现明显峰值,通过检测方法获得峰值所在区域,从而对瞬时频率和瞬时调频率实现估计。基于人工设计特征的传统检测器为实现目标有无的判断,往往依赖于一定的人为假设。但传统检测器对于受到噪声影响或信号分量之间的相互干扰时FFRR生成伪峰或发生散焦情况存在明显的局限性,易发生漏检、误检情况如图5所示。近年来,以数据驱动为基础的深度学习检测算法,减少了人工干预过程,可以实现最优特征的自主学习与分类,通过融合多维度特征实现高性能检测。本文采用改进的YOLOX检测器[25]对峰值所在区域进行检测。YOLOX检测器具有优异检测性能,但FFRR平面峰值目标外形特征简单且可判别特征少,高维特征对于定位精度提升有限,本文在原有YOLOX网络基础上调整输入检测层的特征,减少高维抽象特征,增加了低维细节特征,提高定位精度。

图5 FFRR平面散焦和伪峰情况Fig.5 Defocus and pseudopeak cases in FFRR plane

YOLOX检测器以DarkNet-53作为特征提取网络,DarkNet-53输出4种尺度特征图,其尺寸相对于原始图片尺寸I分别为I1=1/4I,I2=1/8I,I3=1/16I,I4=1/32I。YOLOX选用I2、I3、I43种尺度特征图通过路径聚合网络(path aggregation network, PAN)按自底向上和自顶向下两条路径融合多尺度特征增强了骨干网络的表征能力[26]。对于二维FFRR检测过程中所有分量视为同一类目标,因此对于检测过程仅仅关注于目标定位精度。通过特征提取网络可输出多尺度特征,高层的特征语义信息丰富,但对于目标定位较为粗略。低层的特征语义信息匮乏,但是对目标定位更为精确。即过小的特征图不利于目标定位。为此,将 特征层加入PAN构建新的底层路径聚合分支,并增加对应检测层,同时删除一定高层路径聚合分支并删除对应检测层。通过上述调整实现对目标的更精确定位。具体改进如图6所示,其中红色部分为新增模块,蓝色部分为删减模块。

图6 YOLOX网络结构改进示意图Fig.6 Schematic diagram of YOLOX network structure improvement

改进的YOLOX检测器通过骨干网络和特征聚合网络中提取并融合了多尺度多维度的区域特征,之后基于提取的特征实现目标检测任务。该任务通过YOLOX网络的检测头部分实现,检测头被分为3个分支,分别用于目标定位、目标分类、前景背景的判断。目标定位分支输出四维向量,用于对目标框的坐标信息(cx,cy,w,h)进行预测,其中cx、cy、w和h分别为检测框中心横坐标、中心纵坐标、宽度和高度。对于目标分类分支,由于所有分量都视为同一物体,即只存在一类目标,因此输出只包含一维向量。前景背景判断分支输出为一维的置信度,置信度代表存在物体的概率,经过Sigmoid函数后其值被限制在(0,1)。由此检测头输出为一系列目标候选框,每个候选框为上述六维向量的组合,通过设置置信度阈值可以筛选出符合条件的候选框,通过非极大值抑制[27]过程找出最佳候选框作为目标的检测框。

上述深度学习检测器依赖有标签数据进行监督训练,标签数据可通过对特征区域标注边界框获得。本文将特征区域视为具有固定大小的矩形区域,矩形区域边界即为边界框。区域中心坐标(cx,cy)可由瞬时频率、瞬时调频率获得。由于信号分量大小几乎不随时间改变,由此可将特征区域的长宽w,h均设为定值。

为消除不同信号所生成数据之间存在的差异性,首先对图像进行标准化预处理。对输入图像每一像素a进行

(11)

式中:amax、amin分别为当前图像中像素最大值和最小值。经过标准化后图片中所得像素a′∈[0,1]。待检目标外形特征简单且相似,但目标像素面积小,所包含判别性特征少,检测难度大。为增加待检测的小目标可判别特征,可采用图像插值增大图像分辨率,提高检测精度。

当采用上述YOLOX检测器对FFRR进行检测后,可得到当前时刻各信号分量所在的峰值区域。通过求取检测所得区域中心或者区域最大值得到位置坐标,将位置坐标进行转换得到瞬时频率和瞬时调频率。区域最大值可以通过式(8)进行求解,该位置转换所得瞬时频率和瞬时调频率对应表征所用LFMS的瞬时频率和瞬时调频率,但该估计值对于高阶分量往往存在较大偏差。而经过有监督训练过程的神经网络,综合了峰值区域形状特征、幅值特征等多维特征,所得区域中心对于瞬时频率和瞬时调频率估计更为精确,如图7所示。基于区域中心的瞬时频率和瞬时调频率IFR估计公式为

图7 特征区域示意图Fig.7 Feature region diagram

(12)

(13)

2.2 基于跟踪的多分量信号关联

对于单分量信号,通过上述检测方法即可实现瞬时频率和瞬时调频率估计。然而在多分量情况下,为得到不同分量在所有时刻瞬时频率,需要对每一时刻瞬时估计值进行时序关联。聚类算法和跟踪算法是实现时序关联的有效途径。本文基于卡尔曼滤波算法,通过计算当前时刻的目标检测框和由卡尔曼滤波算法生成的预测框之间的位置相似度实现多分量信号关联。

2.2.1 卡尔曼滤波算法的预测过程

卡尔曼滤波算法通过前一时刻的预测状态和当前时刻的观测状态实现对当前时刻目标信息的最佳估计。对于信号分量在单位采样时间内瞬时频率和瞬时调频率变化往往很小,可近似看作匀速运动,因此可采用匀速模型建模。设t时刻对FFRR检测所得某目标检测框Dt=(cx,cy,w,h),建立如下观测矩阵:

r=[cx,cy]

(14)

为详细描绘目标的运动状态,进一步引入上述信息的变化量,即单位时间x和y方向位置变化值vx和vy,由此状态矩阵可表示为

u=[cx,cy,vx,vy]

(15)

(16)

(17)

式中:上角标T为转置。

(18)

(19)

式中:K为卡尔曼增益,用于估计误差的重要程度,可表示为

(20)

式中:rt+1和cov(rt+1)为t+1时刻观测矩阵和协方差。

2.2.2 基于位置相似度的关联过程

(21)

为使检测框与预测框生成尽可能多地配对并使所得配对具有尽可能高的匹配度,将基于交并比的检测框和预测框的关联匹配问题转化为可以通过匈牙利算法[28]解决的指派问题。匈牙利算法将所得检测框和预测框视作图中两类节点,将节点之间某一相互关系视为节点之间距离。通过使节点之间距离最小化求出检测框与预测框最佳组合。经过转化的IOU可视为节点间距离,为将求IOU之和最大值问题转换为求最小距离和问题,定义损失矩阵M为

M=1-IOU

(22)

式中:1为大小为P×Q元素为1的矩阵。

将损失矩阵M中数值作为各节点之间距离,通过匈牙利算法使得各分量预测框与检测框所表征节点距离之和最小,则可得到各分量的最佳关联。

(23)

3 实验及结果分析

(24)

3.1 单分量信号性能评估

选取SFMS、LFMS和3次相位信号(cubic phase signal, CPS)3类非平稳信号用来验证所提算法性能,分别表示为

x1(t)=A1(t)exp(j2πAsin(2πfvt))·exp(j2πfoffsett)

(25)

x2(t)=A2(t)exp(j2π(f1t+f2t2))

(26)

x3(t)=A3(t)exp(j2π(f5t+f4t2+f3t3))

(27)

式中:A1(t)、A2(t)、A3(t)为幅度调制函数。

A1(t)=cos(2π·0.01t)

(28)

A2(t)=cos(2π·0.01t+0.05π)

(29)

A3(t)=cos(2π·0.02t-0.05π)

(30)

信号观测时间设为1 s,对任一信号xi(t)以采样频率fs=512 Hz进行采样,将离散信号表示为xi(n)(n=0,1,…,N-1),N为信号采样点数。含噪信号si(n)可表示为si(n)=xi(n)+w(n)。在每次仿真中,信号xi(n)按表1中参数所设区间随机生成。

表1 变量取值范围Table 1 Variable value range

如表2所示,用基于VA的估计算法、基于短时稀疏表征(short-time sparse representation, STSR)的估计算法与本文所提基于检测跟踪的瞬时调频率估计算法进行比较。VA本质上是一种通过全局搜索找出最短路径的算法,通过找出时间-频率平面或者时间-调频率平面中分量曲线实现瞬时频率或者瞬时调频率估计。时间-频率表征由STFT生成,窗函数选用窗长为65的汉明窗,时间-调频率表征通过CPF生成。STCFT采用窗长为115的矩形窗,进行NFFT=256点傅里叶变换,则任一时刻所生成二维FFRR大小为256×256。当SNR=10 dB时,图8(a)、图8(c)、图8(e)分别为LFMS、SFMS和CPS时频图,图8(b)、图8(d)、图8(f)分别为信号在n=N/2时刻对应瞬时频率-瞬时调频率表征。在时频平面,LFMS、CPS和SFMS的瞬时频率随时间变化,在时频平面分别展现出直线、二次曲线、正弦曲线。在n=N/2时刻,LFMS和CPS信号在频率-调频率平面出现明显峰值,表现出良好的聚集性。而对于更高阶的SFMS信号,其FFRR则出现明显的散焦和变形。为验证深度学习检测器性能,以传统参量检测器恒虚警率(constant false-alarm rate, CFAR)[29]与本文所用改进的YOLOX检测器进行比较。CFAR算法采用单元平均CFAR(cell average CFAR, CA-CFAR)算法,其核心思想是通过对所设定的参考单元内采样数据取平均来估计背景功率。实验中,CA-CFAR设定的外围保护单元大小为11×11,参考单元大小为21×21,算法通过pytorch实现。通过调优检测器门限因子α设为1.85。

表2 单分量信号参数估计比较方法Table 2 Comparison methods of single component signal parameter estimation

图8 单分量信号时频图及n=N/2时刻FFRRFig.8 Time-frequency diagram and FFRR at the instance of n=N/2 of single component signal

首先,将FFRR进行双线性插值提高图像分辨率,使其大小变为512×512。对于检测器所生成检测区域,可采用所检测出区域中心点或区域像素最大值点表征瞬时估计值位置。对于采用区域像素最大值作为瞬时估计值方案,CFAR检测器与YOLOX检测器具有相似性能。为避免重复分析,CFAR检测器以区域最大值作为表征,YOLOX检测器以区域中心作为表征。对于漏检时刻,采用第2.2节所述插值方法进行补齐。

(31)

式中:L为实验总次数。

实验所用信噪比范围为-5 dB到15 dB,以2 dB为间隔,对每个信噪比进行L=100次实验,每次实验所用参数均为表1所设参数范围随机选取。实验结果如图9和图10所示。由于STCFT实质为用二阶信号对短时信号进行表征,因此在实验所用3种信号中所有方法对于LFMS估计精度最高。所提算法在低信噪比时,二维频率-调频率平面仍然能显示明显峰值,因此该算法受信噪比影响较小,而基于VA的IF估计性能受所生成时频图像分辨率影响较大,同时受信噪比影响变化剧烈。CFAR检测器对于3类信号均能实现较高精度估计,但由于受频率分辨率影响,基于CFAR检测器所检测出区域最大值点为整数索引,其精度受限。而YOLOX检测器可返回更为精确的坐标信息,精度大幅度提高。对于IFR的估计有着相似结果。基于STSR的估计方法先将信号调频率进行补偿再求取瞬时频率对于LFMS的估计有着最高精度,但对于高阶信号由于补偿误差存在性能有所下降。CPF对于LFMS、CPS有着优异的估计精度,但无法适用于更高阶信号,因此其对于SFMS性能较差。所提算法由于以二阶信号对短时的高阶信号进行拟合存在误差,因此所生成峰值点存在扭曲变形,其峰值点与真实值存在偏差难以进行精确估计。

图9 单分量信号瞬时频率估计RMSE随信噪比变化曲线Fig.9 RMSE of IF estimation versus signal to noise ratio of monocomponent signal

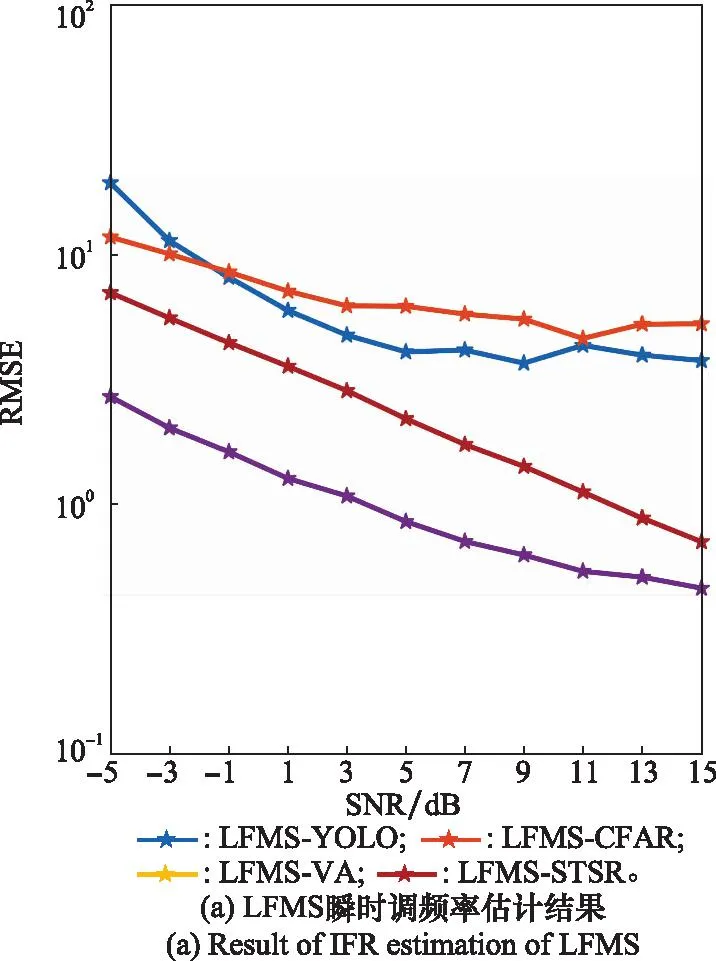
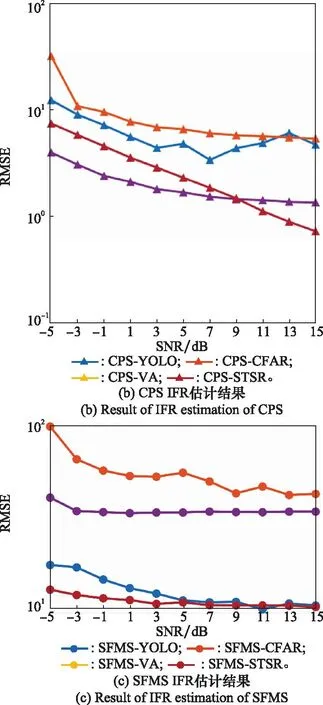
图10 单分量IFR估计RMSE随信噪比变化曲线Fig.10 RMSE of IFR estimation versus signal to noise ratio of monocomponent signal

对于信号IF估计,所提方法对于LFMS估计性能最佳,所有信噪比下的平均RMSE小于0.4 Hz,CPS平均RMSE小于0.6 Hz;SFMS误差最大,所有信噪比下平均RMSE约为0.8 Hz,但仍优于对比算法最小误差。对于IFR估计,相较于对比算法所提算法误差较大,但对于多分量信号所提算法将展现其优越性。

3.2 多分量信号性能评估

对于多分量信号选用第3.1节所述3类信号的叠加信号作为研究对象,其可表示为

(32)

多分量信号同样用表1中所设定参数生成。相比单分量情况下,多分量信号在时频域相互交叉、叠掩难以区分。而在频率-调频率平面可将多分量信号进行有效区分。但在频率-调频率平面,信号分量往往相互干扰,所生成的旁瓣相互交叠生成伪峰,增大了检测难度。通过所提检测跟踪算法可将伪峰滤除,保留真实信号。

如表3所示,以基于短时傅里叶变换的路径重组算法(short time Fourier transform based ridge path regroup, STFT-RPRG)、基于短时傅里叶变换的维特比算法(short time Fourier transform based Viterbi algorithm, STFT-VA)和基于短时稀疏表征(short-time sparse representation, STSR)的估计算法与本文所提算法对于多分量信号IF估计进行对比。STFT设置与第3.1节中相同。

表3 多分量信号参数估计比较方法Table 3 Comparison method of multicomponent signal parameter estimation

检测结果如图11所示,其中红色实线及绿色、蓝色、黄色虚线分别为信号x1、x2、x3真实值和估计值。可以看出IF估计在信号分量相近处、相交处均能有效分离,实现高精度估计。基于STSR的估计算法对于SFMS信号精度明显低于所提算法。受分辨率影响,所提算法基本能实现IFR估计,但精度仍然还有提升空间。

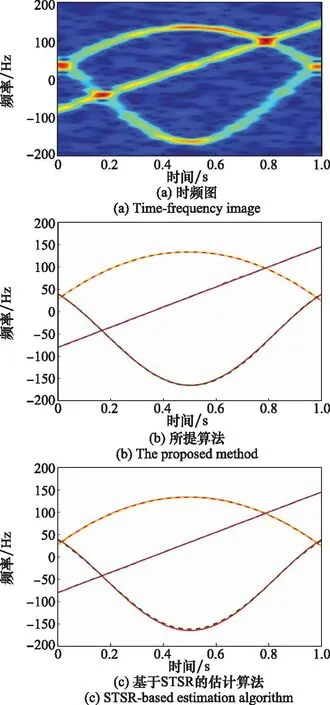
图11 三分量信号估计结果Fig.11 Estimation results of three-component signal

如图12所示,在-5 dB时,本文所提算法RMSE约为0.78 Hz,远优于对比算法;在15 dB时,本文所提算法均方误差约为0.47 Hz。而3类对比算法在所用信噪比条件下RMSE均高于1 Hz,验证本文所提算法在所有信噪比下均实现性能最优。本文所提算法对于IFR估计RMSE约为10～12 Hz/s。而对比方法在所有信噪比RMSE高于30 Hz/s。RPRG和VA算法实现简单但其受信噪比影响较大,对于多分量估计精度更低。

图12 三分量信号IF、IFR估计RMSE随信噪比变化曲线Fig.12 RMSE of IF/IFR estimation versus signal to noise ratio of 3-component signal

上述实验主要针对所提算法在不同信噪比条件下性能与其他算法进行比较。进一步,为分析所提方法在不同仿真参数条件下的性能,通过改变信号窗长并对其结果进行分析,并从中选取最优窗长如表4所示。

表4 窗长对所提算法影响Table 4 Influence of window length on the proposed algorithm

3.3 实测数据验证

将基于仿真数据训练的模型直接迁移用于实测数据,对所提算法进行验证。实验场景如图13(a)所示。实验场景放置两个相对于同一个旋转中心进行旋转的圆柱形目标,对所得信号进行时频分析得到时频图,如图13(b)所示。随着转台旋转,信号呈现出正弦形式变化,在时频平面发生相交。由于受物体表面包裹铝箔不均匀的影响,两目标产生的微多普勒信号强度也呈现出周期性变化。两目标所得信号可视为相位相反的SFMS信号,对所得信号进行STCFT,并对所得TFRR用所提检测-跟踪方法进行瞬时频率、瞬时调频率估计,结果如图13(c)所示。实验所用雷达设备为中心频率77 GHz的毫米波雷达,转台以40 rpm匀速旋转,雷达参数设置如表5所示。

表5 雷达参数设置Table 5 Radar parameters setting

图13 实验场景及实验结果Fig.13 Experimental scenes and results

两个信号分量在TFFR平面呈现出两条不相交的螺旋线,由此可将两分量区分。将所得结果投影到时间-频率平面。由图14可以看出,基于三维表征的估计算法相比基于二维表征的估计算法估计精度更高。相比VA算法和RPRG算法,本文所提算法在不经过平滑处理情况下,提取的曲线在交点处过渡更加自然,整体曲线更加平滑。基于STSR的估计算法在信号末端出现了模糊现象,而所提算法仍能有效分离。

图14 IF估计结果Fig.14 Results of IF estimation

逆约旦变换[30]可实现标准正弦调频信号的参数估计,对非标准正弦调频信号将有较大的估计偏差。上述实测数据所包含的信号分量是非标准正弦调频信号。为此,在利用逆约旦变换前先对信号进行分段,使每一段信号可近似为标准正弦调频信号,并将每一段估计值作为参考值量化评估所提方法。此外,在实际应用中为提高运算效率,往往并不需要对全部信号分析。在不同下采样倍率下分析运行时间和估计精度,结果如图15所示,其中倍率为1代表未进行下采样。随着下采样倍率增加,运行时间不断降低,估计精度在下采样倍率小于4时几乎不改变,在大于6时由于出现无法关联等情况误差陡增,因此对该数据其下采样倍率选取应不大于6。

图15 RMSE和运行时间随下采样倍率的变化Fig.15 RMSE and run time varies with down-sampling rate

进一步对比不同算法运行效率和估计精度。如表6所示,基于三维表征的估计算法往往有着更高估计精度,同时具有更高的复杂度。而本文所提算法在精度提升的同时运行效率也更高。

表6 运行时间和RMSE结果对比Table 6 Comparison of run time and RMSE

本节通过仿真和实测数据验证了所提算法性能。相较于现有算法,本文所提算法估计精度更高,鲁棒性能好,通过仿真数据训练的神经网络直接迁移用于实测数据,仍能获得良好的估计性能。

4 结束语

本文提出一种基于检测-跟踪的多分量瞬时频率-瞬时调频率估计算法。首先通过STCFT将信号以TFFR三维信息进行表征,在三维TFFR空间信号分量可视为具有时序变化频率-调频率属性的多目标。本文将改进的YOLOX网络替代传统检测器实现了信号瞬时频率-调频率的估计和瞬时形状特征的提取,在此基础上通过卡尔曼滤波算法将瞬时估计值进行时序关联,从而获得稳定连续的多分量IF和IFR估计。所提算法具有更高精度、更鲁棒的估计性能。通过仿真实验和实测数据验证了所提算法的有效性。然而,本文仍然存在诸多值得改进之处,如进一步提高算法运行效率等,接下来将针对这些问题进行进一步研究。