环境监测化学需氧量测定结果质量的影响因素研究

＊李源辉

（福建省海峡环境检测有限公司 福建 362000）

不确定度代表了测定结果的不确定性，它反映了测定结果的可能范围，不确定度越小测定结果越可信。某汽修企业接受环保检查时化学需氧量（CODCr）检测结果为152mg/L，排放标准限值为150mg/L，超标2mg/L，应给予罚款10万～100万元。因真值无法获得，企业申请报告检测不确定度，给出的扩展不确定度为6mg/L（k=2）。这意味着废水试样中CODCr含量在146mg/L与158mg/L之间，无法认定企业超标排放，生态环境部门不对企业做出处罚。由此可见，当测定结果被作为决策依据时对测定结果的质量评价就极其重要。为探究实验室CODCr测定结果质量的影响因素，依据HJ 828—2017《水质 化学需氧量的测定 重铬酸盐法》[1]对不同浓度样品均进行9次重复测定，在测定过程中将不同平行测定次数的测定结果运用简化《测量不确定度表示指南》的方法（GUM法）对引入的不确定度进行评定分析，根据引入的不确定度大小判定影响测定结果质量的主要因素。测定现场环境温度设定20℃±3℃，本次测定样品为标准样品不考虑样品干扰引入的不确定度。

1.主要仪器试剂

分析天平：感量0.1mg；容量瓶：250mL、500mL、1000mL；单标线吸量管：5mL、10mL、50mL；滴定管：50mL；重铬酸钾：基准试剂，含量99.95%～100.05%；标准样品A：（33.6±2.8）mg/L（k=2）；标准样品B：（92.9±5.0）mg/L（k=2）。所用玻璃仪器准确等级均为A级，标准温度均为20℃。

2.测量模型

(1)重铬酸钾标准溶液浓度计算公式

式中：m重铬酸钾称取质量，g；ω重铬酸钾基准试剂纯度，%；103重铬酸钾质量以mg为单位的换算系数；M重铬酸钾的摩尔质量，g/mol；Vd1配制重铬酸钾标准溶液的定容体积，mL；1/6，⅙K2Cr2O7浓度的换算系数。低浓度重铬酸钾由高浓度重铬酸钾稀释10倍制得。由测量模型（1）可知，重铬酸钾溶液浓度的不确定度主要由重铬酸钾称量、重铬酸钾试剂纯度、重铬酸钾摩尔质量、配制重铬酸钾溶液定容体积引入。低浓度重铬酸钾溶液浓度的不确定度在前述的基础上增加了高浓度重铬酸钾溶液取样量和低浓度重铬酸钾溶液定容体积的引入。

(2)硫酸亚铁铵标准溶液浓度计算公式

式中：C1重铬酸钾标准溶液浓度，mg/L；5.00为重铬酸钾标准溶液取样量，mL；Vd2滴定时消耗硫酸亚铁铵溶液的体积，mL。根据测量模型（2）结合检测标准可知，硫酸亚铁铵溶液浓度的不确定度主要由重铬酸钾溶液浓度、重铬酸钾溶液取样量、滴定时消耗硫酸亚铁铵溶液体积、标定重复性引入。

(3)样品中化学需氧量的质量浓度计算公式

式中：C2硫酸亚铁铵标准溶液的浓度，mol/L；V0空白实验所消耗的硫酸亚铁铵标准溶液的体积，mL；V1水样测定所消耗的硫酸亚铁铵标准溶液的体积，mL；V2加热回流时所取水样的体积，mL；f样品稀释倍数；8000，¼O2的摩尔质量以mg/L为单位的换算值。测定结果小于100mg/L时保留至整数位。根据测量模型（3）结合检测标准可知，化学需氧量测定结果的不确定度主要由硫酸亚铁铵溶液的浓度、空白实验所消耗的硫酸亚铁铵溶液体积、水样测定所消耗的硫酸亚铁铵溶液体积、所取样品体积、氧的摩尔质量、样品稀释、空白重复性、样品测定重复性、测定结果修约引入。

3.不确定度分量的评定

测定结果均在标准样品证书规定浓度范围内，测定结果均有效。

(1)重铬酸钾标准溶液配制引入的不确定度

①重铬酸钾基准物质称量引入的不确定度

电子天平校准证书显示在（0～50）g的称量范围内，天平的示值误差均为0mg，扩展不确定度为0.17mg（k=2），因此天平本身引入的标准不确定度为u天平=0.17mg/2=0.085mg。对于万分之一的天平称量重复性引入的标准不确定度一般为0.05mg[2]。

②重铬酸钾标准溶液（0.250mol/L）定容引入的不确定度

A.1000mL容量瓶引入的不确定度

B.溶液定容重复性引入的不确定度

运用重量法使用纯水对1000mL容量瓶重复定容10次，统计出其标准偏差为0.202mL，假定其服从正态分布，则其标准不确定度为：0.202mL。

C.温差引入的不确定度

水的体积膨胀系数为2.1×10-4/℃，水的体积膨胀系数远大于玻璃，所以容量瓶定容温差引入的不确定度只考虑前者[6]。实验操作过程中溶液温度变化3℃，假定其服从矩形分布（k=），则其标准不确定度为：（1000mL×3℃×2.1×10-4/℃）/=0.364mL。

合成上述3.1.2.1～3.1.2.3项标准不确定度，则重铬酸钾标准溶液（0.250mol/L）定容引入的标准不确定度为：0.447mL。其相对标准不确定度为：4.47×10-4。

③重铬酸钾标准溶液稀释引入的不确定度

取50.00mL重铬酸钾标准溶液（0.250mol/L）定容到500mL制备（0.0250mol/L）标准溶液。A.量取50.00mL重铬酸钾标准溶液引入的不确定度计算过程同3.1.2，其标准不确定度为：7.58×10-2mL，相对标准不确定度为：1.52×10-3。

B.定容500mL重铬酸钾标准溶液（0.0250mol/L）引入的不确定度

计算过程同3.1.2，其标准不确定度为：0.261mL，相对标准不确定度为：5.22×10-4。

合成上述3.1.3.1、3.1.3.2两项不确定度分量，其相对标准不确定度为：1.61×10-3。

④重铬酸钾纯度引入的不确定度

根据试剂瓶标签其纯度的最大允许误差为±0.05%，将该不确定度按矩形分布处理，则其标准不确定度为：2.89×10-4，相对标准不确定度为：2.89×10-4。

⑤重铬酸钾摩尔质量引入的不确定度

根据IUPAC 2021版的技术报告[7]，重铬酸钾中各元素的原子质量和不确定度如表2所示，按矩形分布考虑，则其标准不确定度为：1.66×10-3g/mol。由表2可得，重铬酸钾的摩尔质量为294.1846g/mol，则其相对标准不确定度为5.64×10-6。

合成3.1.1、3.1.2、3.1.4、3.1.5项的各不确定度分量，则可得重铬酸钾标准溶液（0.250mol/L）配制引入的相对标准不确定度为：5.32×10-4。

合成3.1.1～3.1.5项的各不确定度分量，则可得重铬酸钾标准溶液配制（0.0250mol/L）引入的相对标准不确定度为：1.70×10-3。

综上可知，相对于高浓度重铬酸钾溶液配制而言，低浓度标液配置相对标准不确定度被放大了约3.2倍。

陕西各级政府积极落实国家和陕西省出台的相关促进体育与旅游产业融合发展的政策，如陕西省出台的《关于加快体育产业发展的意见》。建立适应体育与旅游产业融合发展的新体制、机制及规划，真正将体育与旅游产业融合提升到战略性支柱产业位置上。进一步完善各种支持发展政策，引导体育旅游核心产业和支撑产业落户体育旅游产业园区。构建体育与旅游景区经营权和产权的合理关系机制，进一步推动各类金融机构扶持旅游产业中体育项目的开发、经营与合作，拓宽旅游产业的投融资渠道。

(2)硫酸亚铁铵溶液标定引入的不确定度

V(d2低)分别为：24.54mL、24.56mL，V(d2高)分别为：25.19mL、25.21mL。

①量取5.00mL重铬酸钾标准溶液引入的不确定度计算过程同3.1.3，结果见表3。

②硫酸亚铁铵标定过程引入的不确定度

A.仪器本身引入的不确定度计算过程同3.1.2，结果见表3。

B.温差引入的不确定度计算过程同3.1.2，结果见表3。

D.滴定终点判断引入的不确定度

a.理论上，滴定终点与等当点之间将会存在0.1%～0.2%的偏差，考虑不确定度报告的风险性滴定终点误差取0.2%[8]。假定滴定终点的误差为矩形分布，则其引入的不确定度见表3。

b.根据经验用肉眼观测滴定终点颜色可能存在0.5～1滴的偏差，A级50mL滴定管一滴溶液大约为0.04mL，假定其服从矩形分布，则肉眼观测滴定终点颜色引入的不确定度见表3。

合成上述3.2.2.1～3.2.2.4四项标准不确定度，可得硫酸亚铁铵溶液标定过程引入的不确定度，结果见表3。

合成3.2.1、3.2.2项的各不确定度分量，则可得硫酸亚铁铵溶液标定引入的相对标准不确定度，结果见表3。

(3)滴定空白引入的不确定度

V(0低)分别为：21.13mL、21.17mL，V(0高)分别为：25.08mL、25.12mL。滴定空白引入的相对标准不确定度计算同3.2.2，则其相对标准不确定度分别为：urel(3.3低)=2.46×10-3；urel(3.3高)=2.17×10-3。

(4)样品量取引入的不确定度

计算过程同3.1.3，则量取10.00mL样品引入的标准不确定度为：1.39×10-2mL，其相对标准不确定度为：1.39×10-3。

(5)氧的摩尔质量引入的不确定度

由表2可知，氧的摩尔质量引入的标准不确定度为：0.00037g/mol×（）-1=2.14×10-4g/mol。则其相对不确定度为：1.34×10-5。

(6)样品滴定过程引入的不确定度

样品滴定过程引入的不确定度计算近似3.2.2，因考虑了样品重复测定引入的不确定度，所以不考虑滴定体积重复性引入的不确定度，结合表1则样品滴定过程引入的不确定度见表4。

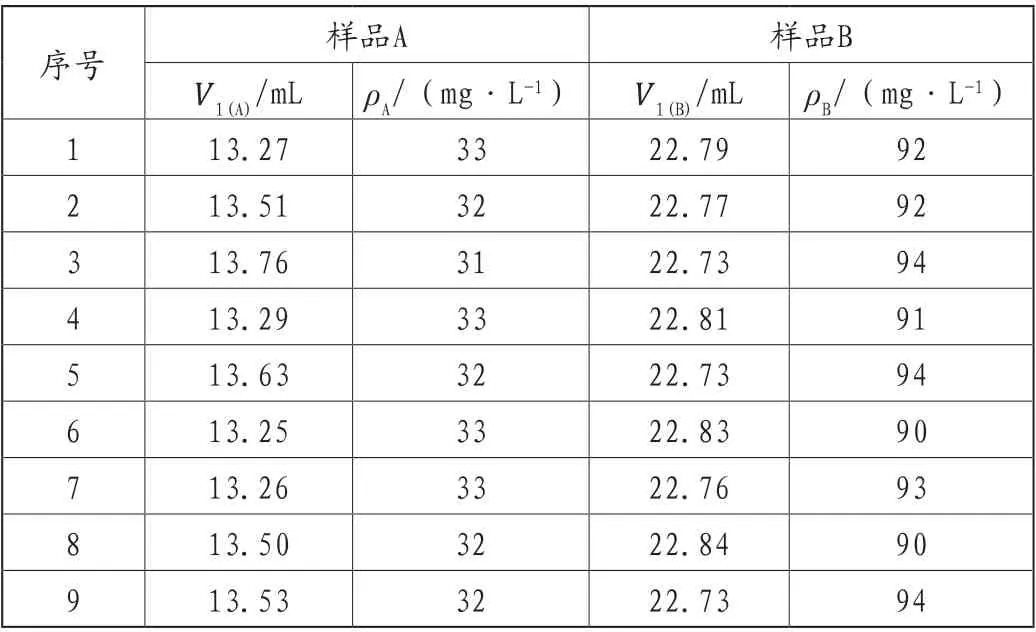
表1 样品测定结果

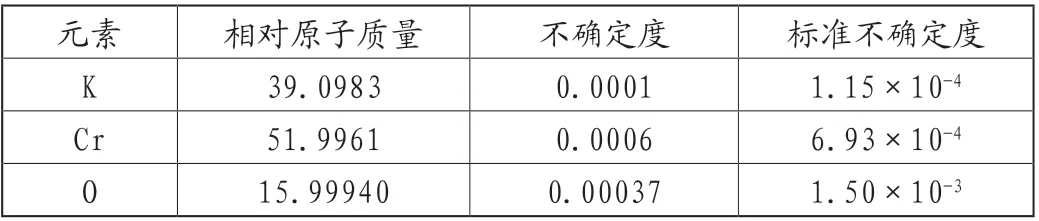
表2 重铬酸钾各元素原子质量不确定度

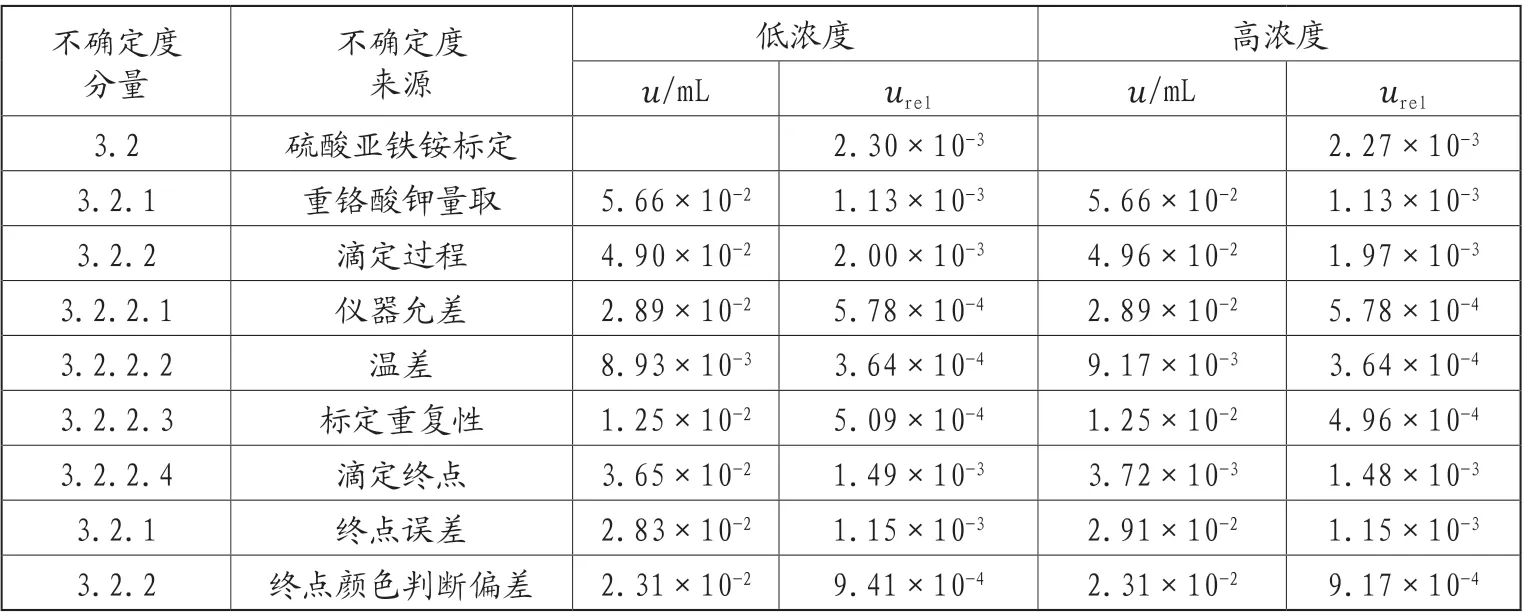
表3 硫酸亚铁铵溶液标定不确定度分量一览表

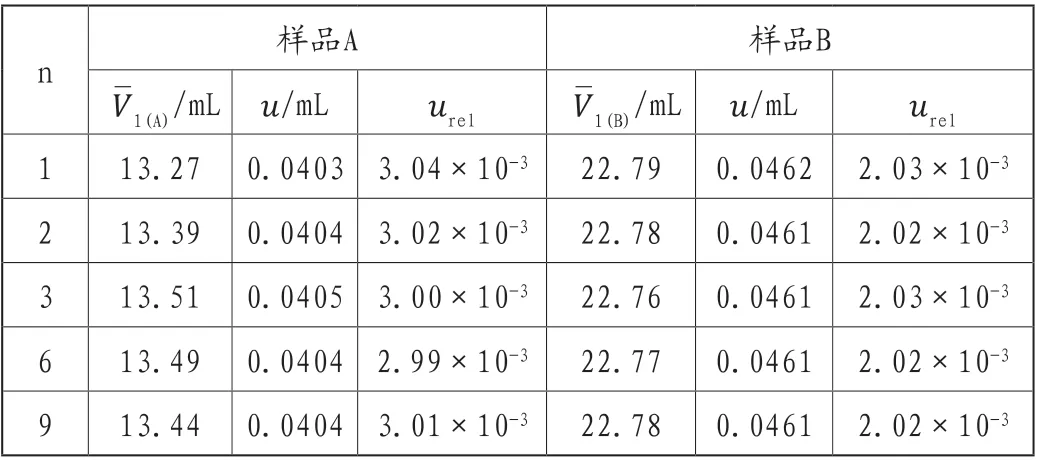
表4 样品滴定过程不确定度

(7)样品重复测定引入的不确定度

根据检测员连续测定的数据评定样品重复测定引入的不确定度，样品重复次数分别为1次、2次、3次、6次和9次。当样品重复测定次数大于等于2次时，使用极差法评定其引入的标准不确定度，u=[Max(ρ)-Min(ρ)]/C×()-1，式中C为极差系数；n为重复测定次数。当样品测定次数为1次时，其标准不确定度根据检测标准所提供的重复性限r结合内插法进行不确定度的B类评定，u=r/2.83[2]。结合表1，则样品重复测定引入的不确定度见表5。

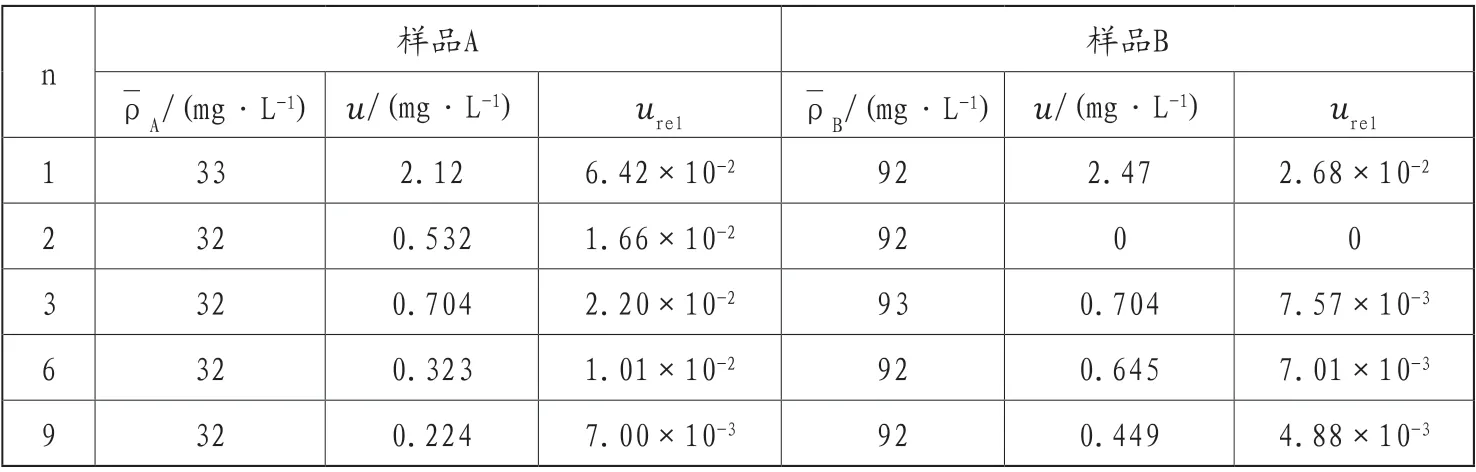
表5 样品重复测定不确定度

(8)测定结果修约引入的不确定度

本次测定结果均修约至整数位[1]。则数值修约间隔为1，修约间隔的分散区间半宽为0.5×1=0.5，假定其按矩形分布，则测定结果修约的标准不确定度为：0.5×()-1=0.289mg/L。结合表5则其相对标准不确定度见表6。

表6 测定结果修约的相对标准不确定度

4.不确定度分量分析与合成

(1)不确定度分量分析

不确定度分量见表7，由表7可知：

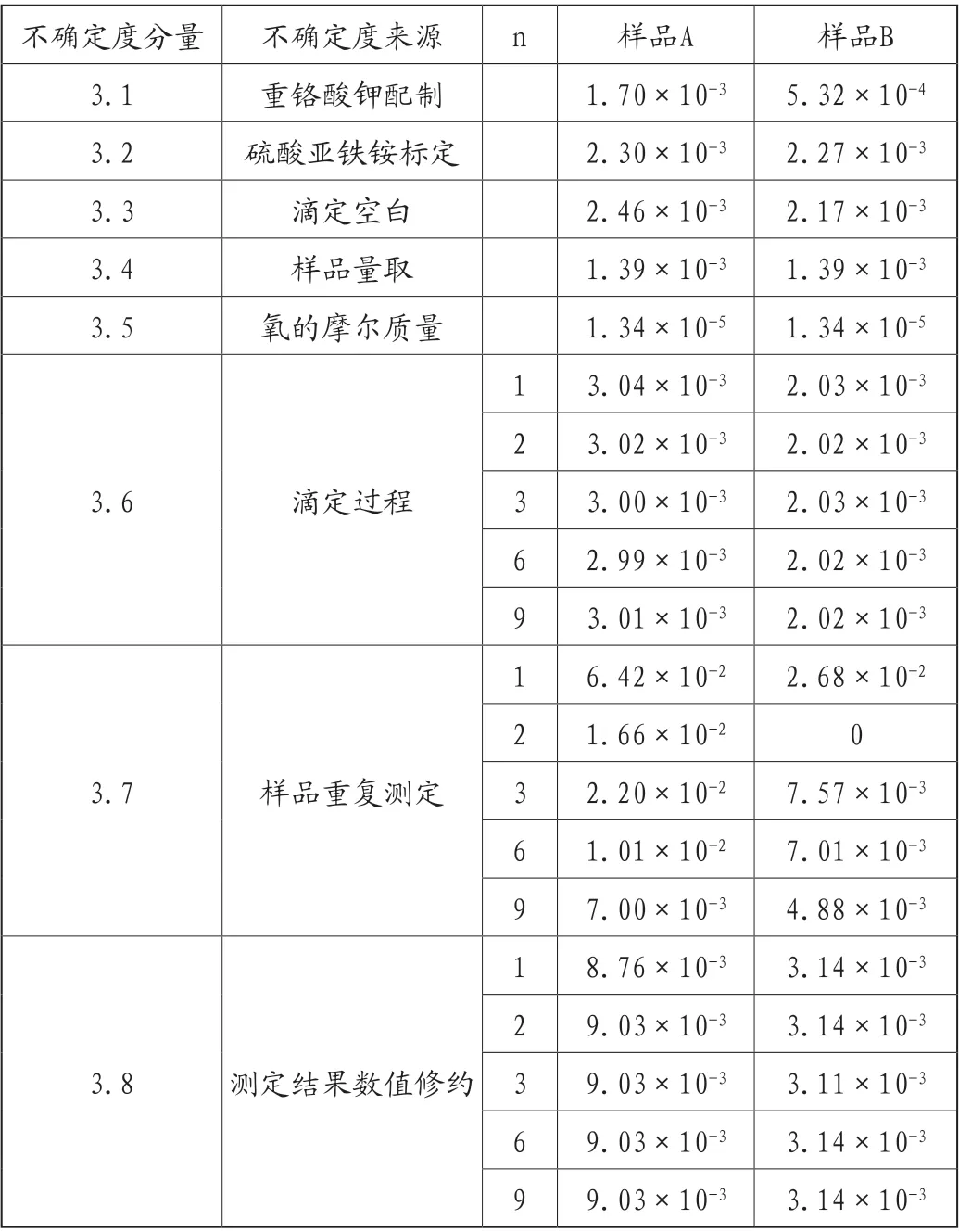
表7 不确定度分量一览表

相对于大于50mg/L的样品测定低浓度样品测定结果的不确定度分量被不同程度的放大。其中，重铬酸钾配制引入的不确定度被放大了3.2倍；滴定过程引入的不确定度被放大了约1.5倍；样品重复测定引入的不确定度被放大了1.4～2.4倍，随着样品重复测定次数的增加放大的倍数逐渐较小；测定结果数值修约引入的不确定度被放大了3倍。平行测定结果的不确定度分量可能存在部分极端情况，以平行测定结果进行样品测定重复性不确定分量的评定存在较大的结果判定风险。

根据表7做贡献度柱状图及柏拉图，分析CODCr测定结果质量的主要影响因素。结果显示：

对样品进行10次以内的重复测定时，其不确定度的主要影响因素是样品测定重复性引入的不确定度以及测定结果修约引入的不确定度，二者贡献度占比达到近50%以上，其中样品测定重复性引入的不确定度大于测定结果修约引入的不确定度。随着样品重复测定次数的增加，由样品测定重复性引入的不确定度存在逐渐变小的趋势。对样品进行3次重复测定时，由样品测定重复性引入的不确定度贡献度发生跃变。当重复测定次数达到9次时，由样品测定重复性引入的不确定度贡献度仍有约30%的占比。

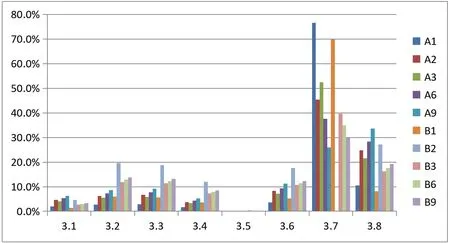
图1 不确定度分量贡献度柱状图

(2)不确定度分量的合成

不确定度分量详见表7，对不同样品浓度和重复测定次数分别为1次、2次、3次、6次、9次，将测定结果的相对标准不确定度进行合成，则合成的相对标准不确定度为：

合成标准不确定度uc(ρ)=urel(ρ)×ρ，取包含因子k=2，则扩展不确定度U=uc(ρ)×2。综合表1，则合成后的不确定度见表8。

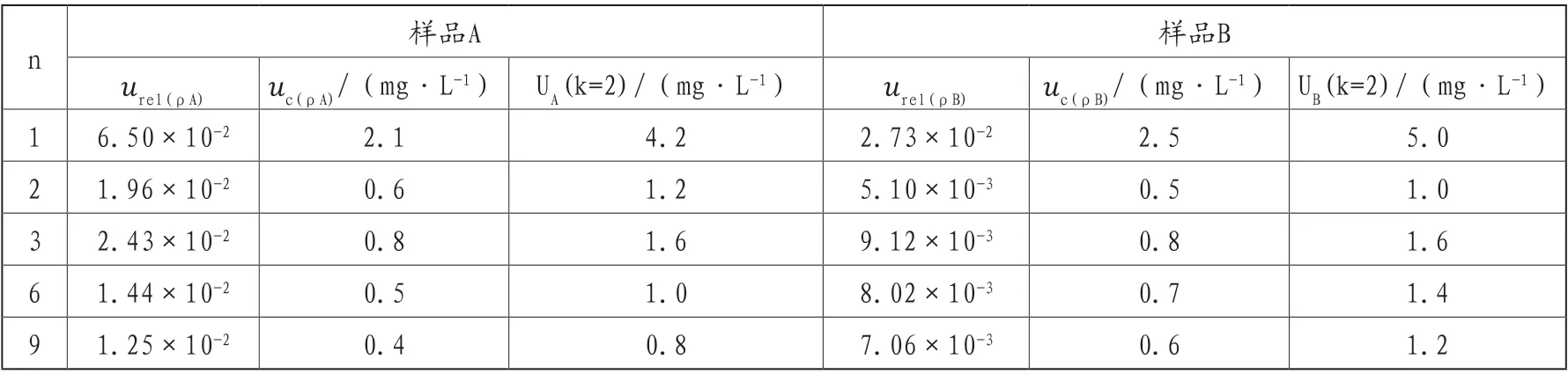
表8 合成后不确定度一览表

由表8可知：多次测定有助于降低测定结果的不确定度，相对于大于50mg/L的样品测定，低浓度样品测定结果的相对标准不确定度被放大了1.7～3.7倍。

5.结论

（1）相对于大于50mg/L的样品测定，低浓度样品测定结果质量均低于高浓度样品，重复测定次数差异相对标准不确定度比值为1.7～3.7倍。

（2）对样品进行10次以内的重复测定时，测定过程中测定结果质量的主要影响因素是样品测定的重复性以及对测定结果进行修约。重复测定次数差异其贡献度占比介于48.8%～87.1%，其中样品测定重复性影响比对测定结果修约大，尤其在测定次数小于3次时最为明显。多次测定有助于提高测定结果质量，样品测定重复性与实验结果的标准差存在较大关联，实验室可将实验结果标准差作为检测人员能力考评的重要依据之一。

（3）当测定结果处于判定标准限值附近时，建议对样品进行至少3次重复测定，并评定报告不确定度。