基于特征差异性学习卷积神经网络的齿轮箱故障诊断方法

2024-01-16石永芳徐庆宏姜宏章翔峰

机床与液压 2023年24期

石永芳，徐庆宏，姜宏，章翔峰

(1.新疆医科大学医学工程技术学院，新疆乌鲁木齐 830054；2.新疆大学机械工程学院，新疆乌鲁木齐 830049)

0 前言

随着工业4.0的快速发展，航空航天、轨道交通、能源动力等领域对机械设备性能提出了更高要求。齿轮箱作为机械传动系统中的核心零件之一，广泛应用于风力发电机、涡轮发动机等旋转机械设备中。由于齿轮箱长期工作在高速、重载的环境下，极易出现故障，而齿轮箱故障可能会导致生产停滞，甚至人员伤亡。因此对齿轮箱进行故障诊断具有重要意义。

齿轮箱传统故障诊断方法主要是先通过信号处理(如包络分析[1]、小波变换[2]、经验模态分解[3]等)提取特征，再利用机器学习模型(如人工神经网络[4]、支持向量机[5]、K最近邻[6]等)进行分类诊断。但这类方法需要大量专家知识以及手动选取特征，且在处理海量异构数据时非常耗时。近年来，深度学习在计算机视觉、自然语言处理等领域取得丰硕成果，受到广泛关注，因此有学者尝试将深度学习应用至故障诊断领域。基于深度学习的智能故障诊断方法可分为大数据收集和深度学习算法诊断两部分[7]。与传统的故障诊断方法不同，基于深度学习的智能故障诊断方法对大量机械数据具有非常强的处理能力，能实现从数据输入到故障识别的端到端故障诊断。经典的智能故障诊断模型主要有自编码器(Auto-Encoder，AE)[8-9]、深度信念网络(Deep Belief Network，DBN)[10-11]、循环神经网络(Recurrent Neural Network，RNN)[12-13]以及卷积神经网络(Convolutional Neural Network，CNN)等。与其他深度学习算法模型相比，CNN具有三大优点：局部感受野、权值共享和池化，有效降低了网络模型的复杂度和过拟合风险，因此CNN在故障诊断领域应用极为广泛。ZHANG等[14]提出一种第一层宽核深度卷积神经网络(Deep Convolutional Neural Networks with Wide first-layer kernels，WDCNN)，在第一卷积层使用宽卷积核提取特征并抑制高频噪声，利用小卷积核提取深层特征，结果表明：该模型对变负载工况和噪声具有一定鲁棒性。吴春志等[15]提出基于一维卷积神经网络(one-Dimensional Convolutional Neural Network，DCNN)的齿轮箱故障诊断模型，实验结果表明该模型故障识别准确率高于传统诊断方法。

但是仅采用深层一维卷积神经网络无法捕捉振动信号的多尺度特征[16]，于是有学者尝试构建可以提取多尺度特征的故障诊断模型。卞景艺等[17]提出基于多尺度一维深度卷积神经网络的故障诊断方法，实验结果表明：该模型准确率相较于DCNN提高1.25%。许子非等[18]提出多尺度卷积神经网络(Multi-Scale Convolutional Neural Network，MSCNN)，并对11种含故障类型、损伤程度不同以及4种存在故障混合的轴承状态进行识别，与现有方法相比该模型在复杂环境下性能更佳。

虽然上述基于MSCNN的故障诊断方法在实际应用中取得了很好的效果，但在每个尺度下均采用相同的特征提取策略，所得特征较为单一，特征差异不大，特征融合后存在冗余特征。且仍面临随着层数加深，模型难以训练，梯度消失现象明显的网络性能退化问题。基于上述问题，本文作者提出一种基于特征差异性学习卷积神经网络(Feature Difference Learning Convolutional Neural Network，FDLCNN)的故障诊断模型。FDLCNN使用不同大小的卷积核提取振动信号不同尺度的特征，每个尺度下使用不同数量的卷积模块提取不同深度的特征。通过提取具有差异性的特征，以有效解决MSCNN特征融合带来的特征冗余问题。利用齿轮箱数据集进行对比验证。

1 理论基础

1.1 特征提取模块

文中使用的特征提取模块包含卷积模块和残差模块。卷积模块结构示意如图1(a)所示，主要包含卷积层、批量归一化层、激活函数层和池化层。

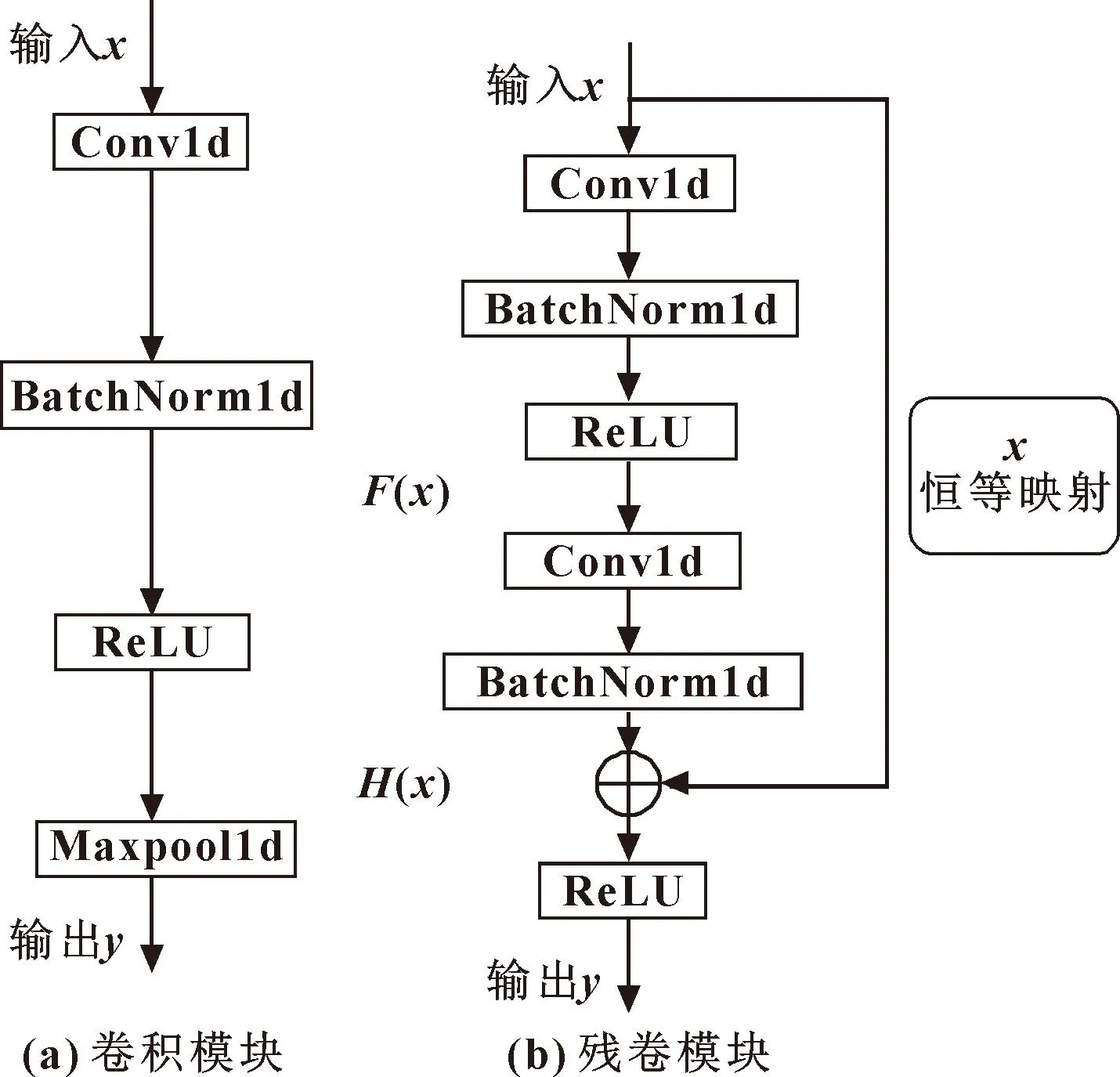
图1 特征提取模块Fig.1 Feature extraction module：(a)convolution module； (b)residual module

卷积层通过使用卷积核对其输入数据的局部区域进行卷积运算，从而实现特征提取。具体的卷积运算如式(1)所示：

(1)

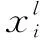
批量归一化(Batch Normalization，BN)层由谷歌研究员IOFFE和SZEGEDY[19]提出，其目的是使每一层神经网络的输入保持相同的概率分布，从而加快网络训练和收敛速度，并且控制梯度爆炸、防止梯度消失、避免过拟合。

激活函数层采用激活函数ReLU，使模型拥有非线性表达能力。具体运算如式(2)所示：

f(x)=max(0，x)

(2)

池化层采用最大池化，池化层是实现池化操作的网络层，也称为下采样层。卷积层提取特征后，直接用于分类将面临巨大的计算量，且容易产生过拟合现象，因此需要对特征图进行池化操作，在进行特征降维的同时保留关键特征信息。相比卷积运算，池化操作不涉及参数设置和内存，计算量也大幅减少。池化操作如式(3)所示：

(3)

HE等[20]提出了残差神经网络(Residual Neural Network，ResNet)，解决了深度卷积神经网络随着网络加深而出现的网络性能退化问题。残差模块的定义如式(4)所示：

y=F(x，{Wi}+x)

(4)

式中：x和y分别为模块的输入和输出；F表示学习的残差映射；Wi表示残差模块参数。

残差模块结构如图1(b)所示，通过跳跃连接，直接将输入x传到输出作为初始结果，而输出结果为H(x)=F(x)+x，当F(x)=0时，H(x)=x，即恒等映射，残差模块的目标是学习H(x)和x的差值。

1.2 故障分类模块

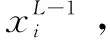
(5)

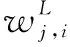
输出层通过Softmax分类器以类别或者概率的形式输出模型的识别结果。对于n个样本，其中i类别的概率Pi计算公式为

(6)

式中：θ(i)为网络模型参数；x为网络模型输出到Softmax的参数。

2 基于FDLCNN的故障诊断方法

基于FDLCNN的齿轮箱故障诊断方法通过改进MSCNN网络结构，并引入残差连接，可实现振动信号到故障类型端到端的故障诊断。

2.1 特征差异性学习卷积神经网络

文中构建的网络架构如图2所示，主要包括输入层、特征提取层和输出层三部分。由原始数据D采样获得样本X1，X2，X3，…，Xn，在输入层中输入样本，特征提取层包含3个尺度，每个尺度获得对应输入X。第一尺度所得特征为f1，第二尺度所得特征为f2，第三尺度所得特征为f3，表达式为

图2 特征差异性学习卷积神经网络架构Fig.2 Feature difference learning convolutional neural network architecture

f1=P1(R1(C13(C12(C11(X)))))

(7)

f2=P2(R2(C22(C21(X))))

(8)

f3=P3(R3(C31(X)))

(9)

式中：Pi表示一维自适应平均池化操作；R表示残差模块；C表示卷积模块。将f1、f2、f3特征融合所得特征F为

F=Concatenate(f1，f2，f3)

(10)

式中：Concatenate表示特征融合。使用全连接层对融合后的特征F降维，最后输入Softmax函数输出故障预测概率P为

P=Softmax(Linear(F))

(11)

特征提取模块中的第一尺度使用小卷积核，获得的感受野小，但含有3个卷积模块，适合挖掘局部和深层特征。第三尺度使用大卷积核，获得的感受野大，只有1个卷积模块，适合挖掘全局和浅层特征。第二尺度的卷积核尺寸适中，有2个卷积模块，用于兼顾提取第一、第三尺度未考虑的其余特征。考虑模型因网络层数加深带来的性能退化问题，引入残差模块，将每个尺度下浅层特征与深层特征结合，提升网络的特征提取能力。FDLCNN可以提取振动数据中不同尺度、不同深度具有差异性的特征，将其进行融合，兼顾了全局信息和局部信息，有针对性地进行特征学习，使网络学习更多与故障状态相关的特征信息，从而更好地做出诊断决策。

2.2 诊断流程

FDLCNN模型采用有监督训练算法，即训练模型时输入带标签的样本。网络训练包含前向传播阶段和误差反向传播阶段。在训练开始前，首先初始化网络的权重参数。在前向传播阶段，将信号输入至FDLCNN中，经过多个尺度的特征提取，获得其故障特征，通过Softmax得到各样本对应的故障预测概率，利用交叉熵损失函数计算故障预测概率与标签之间的误差。在反向传播阶段，通过梯度下降法更新网络权重参数，实现误差反向传播。

图3所示为提出的基于FDLCNN的齿轮箱故障诊断流程，主要步骤如下：

图3 基于FDLCNN的故障诊断流程Fig.3 The fault diagnosis flow based on FDLCNN

步骤1，利用加速度传感器采集齿轮箱振动信号。

步骤2，通过对原始振动信号进行滑窗采样构造样本数据集，并按比例随机划分为训练集、验证集、测试集。

步骤3，构建FDLCNN模型，设定学习率、Batch size、Epoch等超参数，初始化网络权重参数。

步骤4，计算网络实际输出，利用交叉熵损失函数计算故障预测概率与标签之间的误差，根据Adam梯度下降算法反向传播误差，并更新网络权重和偏置矩阵。循环此步骤，直至设定的总训练轮数。其中每训练一轮，便使用验证集对网络进行评估，但不进行误差的反向传播和权重更新。

步骤5，利用测试集评估训练完成的FDLCNN模型。将测试集样本的网络预测值与真实标签进行对比，得到各故障类型的预测概率，取其中概率最大的故障类型作为故障诊断最终结果。

3 实验验证

3.1 数据集描述

为展示所提模型的优越性，利用SQI公司的风电机组驱动系统故障诊断实验台采集齿轮箱故障数据进行对比实验验证。实验台如图4所示，主要包含驱动电机、电机控制器、二级平行轴齿轮箱、行星齿轮箱及磁粉制动器。二级平行轴齿轮箱结构简图如图5所示，齿轮模数为1.5 mm，齿轮箱传动比为8.92，输入轴转速固定为1 500 r/min，实验在负载为0的工况下进行。

图4 风电机组驱动系统故障诊断实验台Fig.4 Wind turbine drive system fault diagnosis test bench

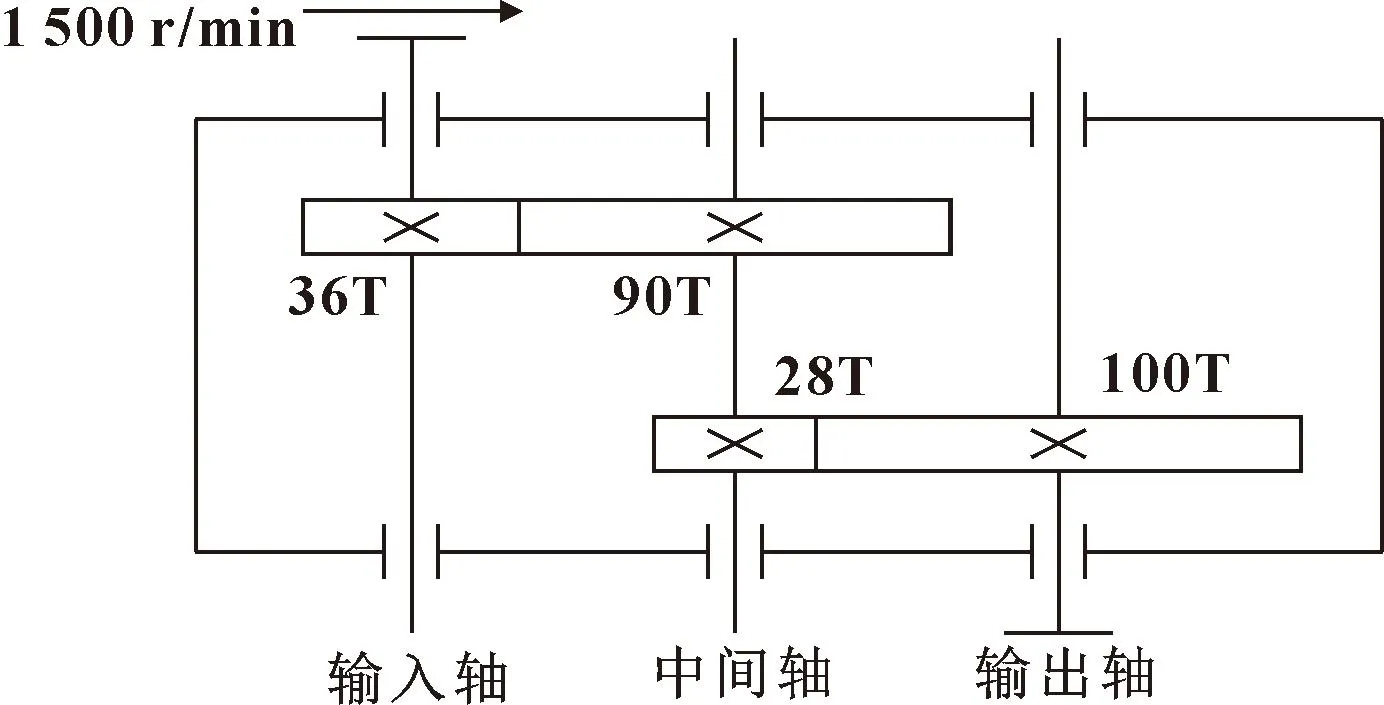
图5 平行轴齿轮箱结构简图Fig.5 Structure diagram of parallel shaft gear box

此次实验的故障齿轮与故障轴承均安装在二级平行轴齿轮箱中，齿轮轴承故障实物如图6所示。齿轮箱状态振动信号由放置在二级平行轴齿轮箱箱体上的加速度传感器收集，采样频率为20 480 Hz，共包含10种齿轮箱状态，其中1类正常状态、7类单故障状态和2类复合故障状态，10类信号时域图如图7所示。样本数据集由滑窗采样而得，滑窗采样如图8所示。此次实验滑窗长度为1 024，窗口移动步长为512，即相邻2个样本之间有512个重叠点，共采得实验样本9 000个，样本详细信息如表1所示，按照8∶1∶1划分为训练集、验证集、测试集。训练集用于训练网络，更新网络参数；验证集用于每轮训练后对模型进行评估，检验模型在训练集上是否过拟合；测试集用于评估最终模型的故障分类性能。

表1 实验样本与标签Tab.1 Experimental samples and labels

图6 齿轮箱故障类型Fig.6 Gearbox fault types：(a)ball fault；(b)inner ring fault；(c)outer ring fault；(d)broken tooth； (e)missing tooth；(f)tooth surface wear；(g)tooth root crack

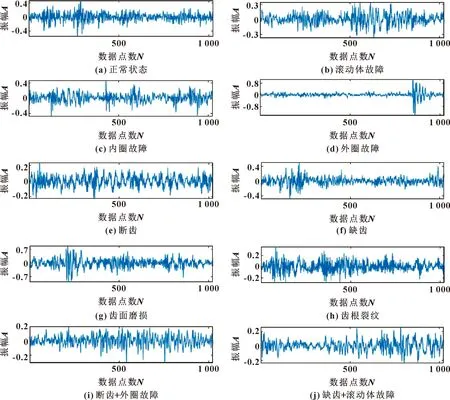
图7 齿轮箱故障信号Fig.7 Gearbox fault signals：(a)normal state；(b)ball fault；(c)inner ring fault；(d)outer ring fault；(e)broken tooth； (f)missing tooth；(g)tooth surface wear；(h)tooth surface crack；(i)broken tooth+outer ring fault； (j)missing tooth+ball fault

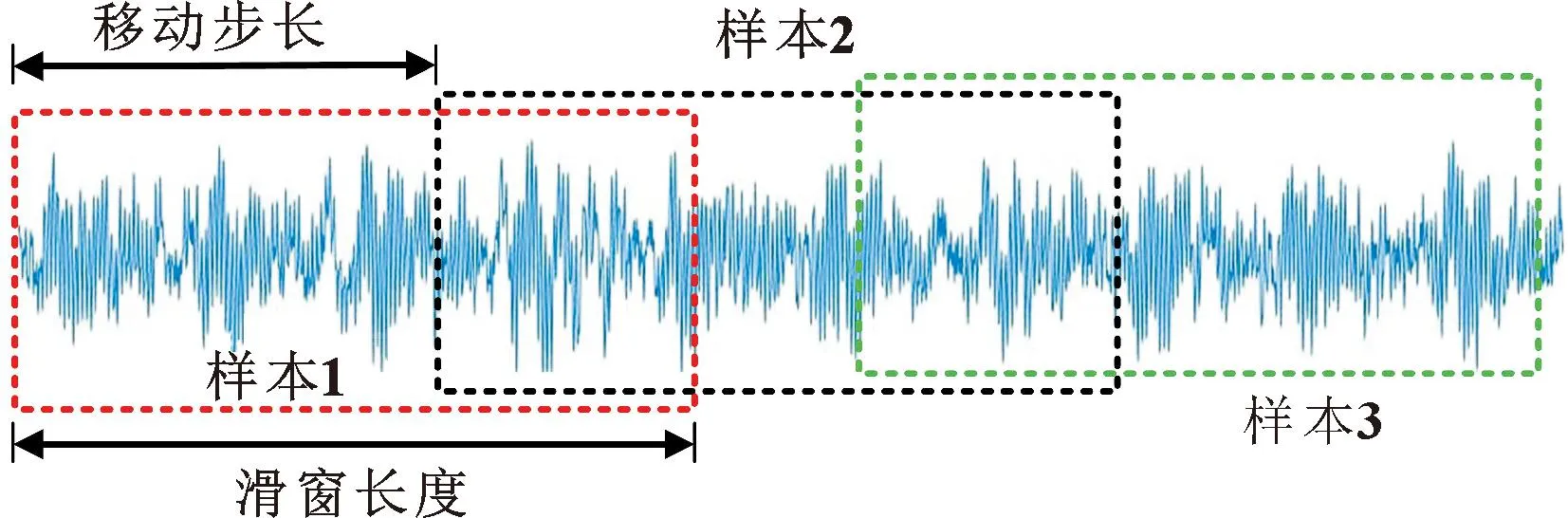
图8 滑窗采样Fig.8 Sliding window sampling

3.2 对比实验

为评估文中所提方法的优越性，将它与多尺度卷积神经网络(MSCNN)、宽核卷积神经网络(WDCNN)和一维卷积神经网络(DCNN)进行比较。为保证实验的可靠性，MSCNN设置为3个尺度，每个尺度上使用3个卷积模块，且每个尺度上第一个卷积核尺寸与FDLCNN对应相同；WDCNN同样使用3个卷积模块，宽卷积核尺寸与FDLCNN第二尺度相对应；DCNN同样使用3个卷积模块，第一个卷积核大小为4。各模型超参数设置一致，即模型学习率0.001，训练轮数10，样本批量大小64，激活函数均采用ReLU。FDLCNN的网络参数如表2所示。

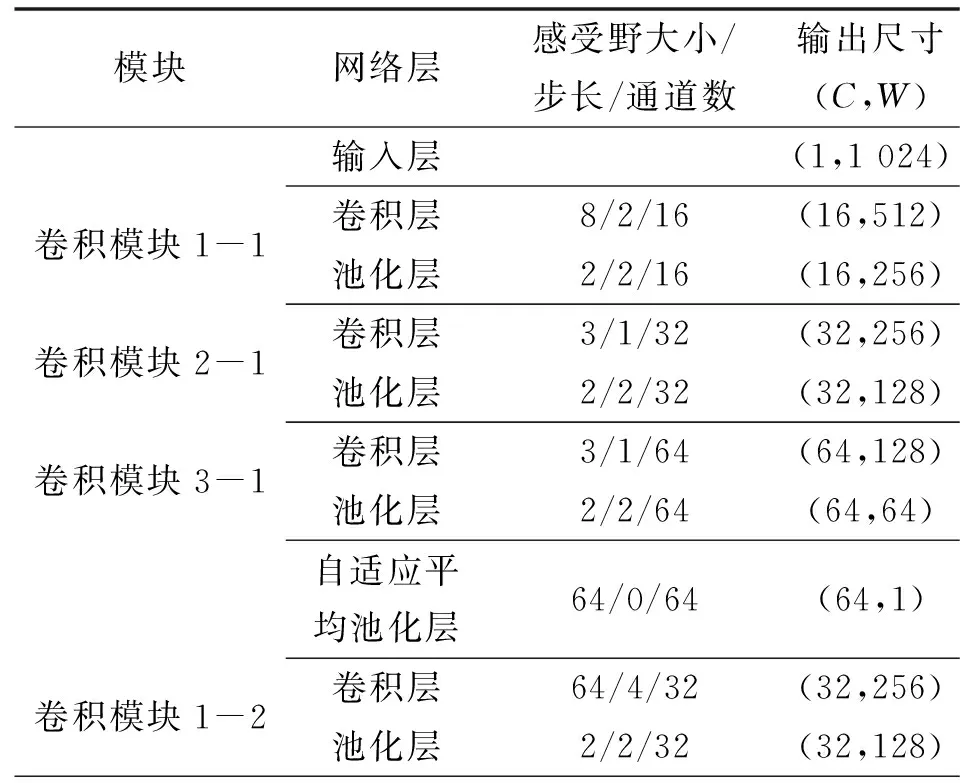
表2 FDLCNN的详细网络参数Tab.2 The detailed network parameters of FDLCNN

3.3 实验结果与分析

训练过程中，各模型在训练集和验证集上准确率变化情况如图9所示。观察各模型在训练集和验证集上的表现，其准确率变化总体呈上升趋势，没有出现严重过拟合。随着训练周期的增加，FDLCNN在训练集上的识别精度趋于平稳，在第三轮训练时，其准确率基本接近100%，并开始逐渐收敛。而MSCNN在第五轮训练时开始收敛，且其准确率在整个训练过程中均低于FDLCNN。这表明使用不同深度的多尺度结构网络能学习到差异性的特征，特征之间没有冗余，有利于提升网络的收敛速度、识别精度和鲁棒性。

图9 准确率曲线Fig.9 Accuracy curves：(a)training set；(b) validation set

为对比模型的故障诊断稳定性，考虑随机初始化参数对深度学习模型性能的影响，模拟实验的最终结果略有波动。因此选择随机初始参数在所有故障诊断模型中进行20次平行实验，以减少实验误差的影响和结果的不确定性，测试集上各模型准确率如图10所示。可以看出：FDLCNN准确率变化平缓，上下波动幅值不超过2%，其稳定性优于其他模型。

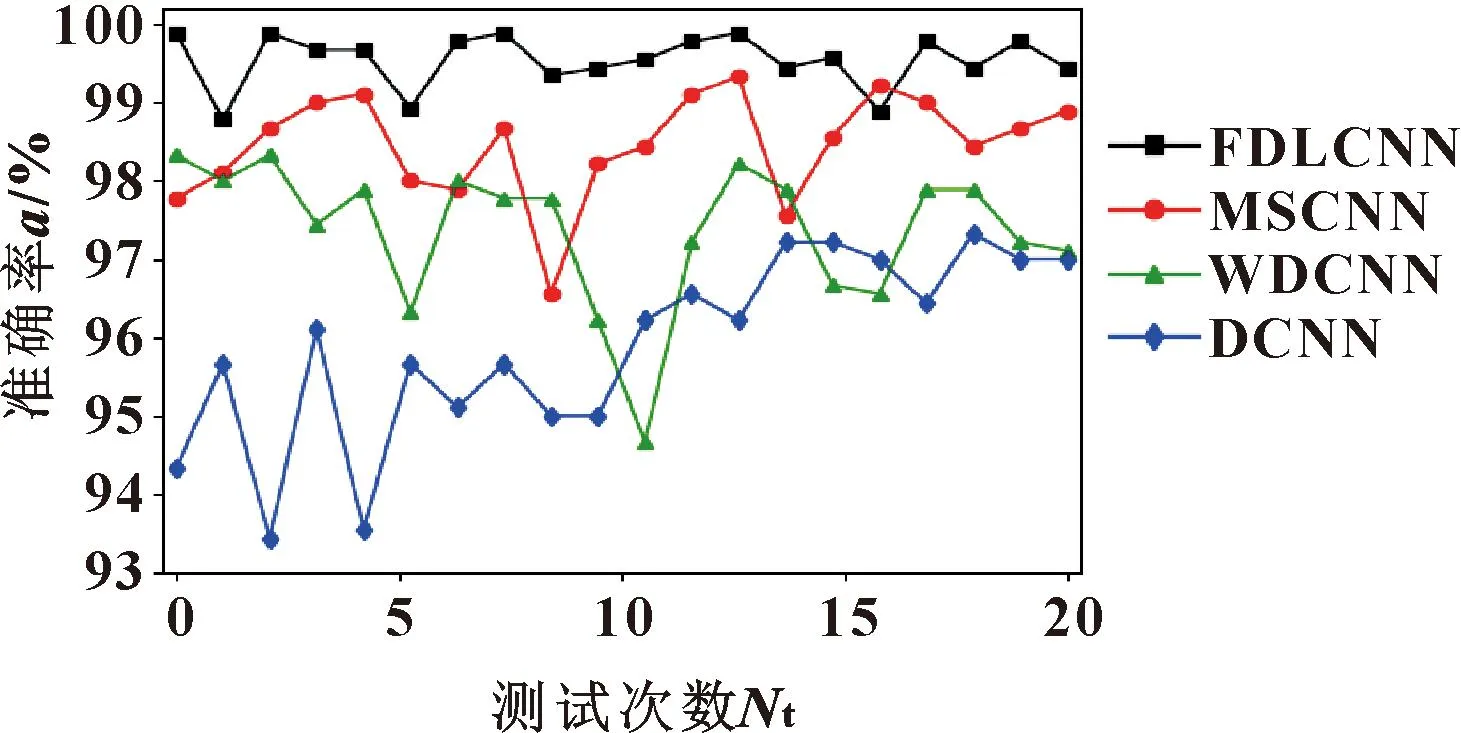
图10 平行实验测试集准确率Fig.10 Parallel experiment test set accuracy

各种齿轮箱状态以及整个测试集的平均准确率及其标准差如表3所示，可以看出：FDLCNN的平均准确率为99.54%，MSCNN的平均准确率为98.46%，WDCNN的平均准确率为97.37%，DCNN的平均准确率为95.88%，均高于95%，说明使用卷积模块的各模型对一维原始故障数据均有良好的特征提取和故障分类效果。但WDCNN和DCNN的故障分类平均准确率出现较大波动，特别是对于滚动体故障、缺齿和滚动体的复合故障，其标准差分别为4.74%、3.66%和3.82%、5.81%，而FDLCNN、MSCNN分别为1.99%、1.24%和3.09%、1.37%，表明多尺度结构网络比单尺度结构网络的特征提取能力和鲁棒性更强。对比FDLCNN和MSCNN在10种故障状态及测试集上的表现可知：使用不同深度的多尺度结构能够提升网络特征的提取能力，此外在多尺度结构基础上使用残差连接也增强了网络的鲁棒性，进一步验证了FDLCNN的优越性。

为了更加直观地显示所提出的FDLCNN模型的优势，使用t-分布随机近邻嵌入(t-distributed Stochastic Neighbor Embedding，t-SNE)将各模型中Softmax分类器的输入特征映射至二维空间，实现特征可视化，所有模型获得的t-SNE可视化结果如图11所示。可以看出：3种模型对于10种齿轮箱状态数据均产生一定的分类错误，而FDLCNN能将10种故障状态的数据完全分开。这表明相比于其他模型，FDLCNN可以获得最大类间隔和最小类间隔，体现出比其他模型更强的特征学习能力。