瓦形磁吸单元磁路设计及其力学特性研究
2024-01-16姚震球安帅凌宏杰朱伦靖
姚震球,安帅,凌宏杰,朱伦靖
(1.江苏科技大学船舶与海洋工程学院,江苏镇江 212003;2.安徽大地熊新材料股份有限公司,安徽合肥 231500)
0 前言
随着我国船舶修造业的高速发展,人力成本不断增加,爬壁机器人船舶清洗、除锈和喷漆等作业研究成为热点。永磁吸附是轮式爬壁机器人的吸附方式之一,具有吸附力大、结构紧凑简单等优点。瓦形结构的磁铁对于轮式机器人至关重要,避免了其与机器人本体发生冲突。国外学者对爬壁机器人的吸附方式进行了讨论[1],TAVAKOLI等[2-3]研制了一款应用于爬壁机器人的永磁轮,将磁体置于全向轮与电机的连接轴上;BISHT等[4]设计了轮式机构,对气隙和试验面厚度变化进行了试验研究。文献[5-9]分析了Halbach阵列充磁方式,如图1所示,该磁路大幅提高吸附效率。MAO等[10]、孙涛等人[11]、FAN等[12]仿真分析了不同磁路及参数的永磁轮,讨论磁吸力的影响条件。郭登辉、陈原[13]设计了一种近似圆弧的磁吸单元,经过仿真计算分析,得出最优磁铁宽度和吸附力。宋伟等人[14]设计了适用于轮式机器人的瓦形吸附单元,如图2所示,并对磁吸附组件参数进行仿真与试验分析。
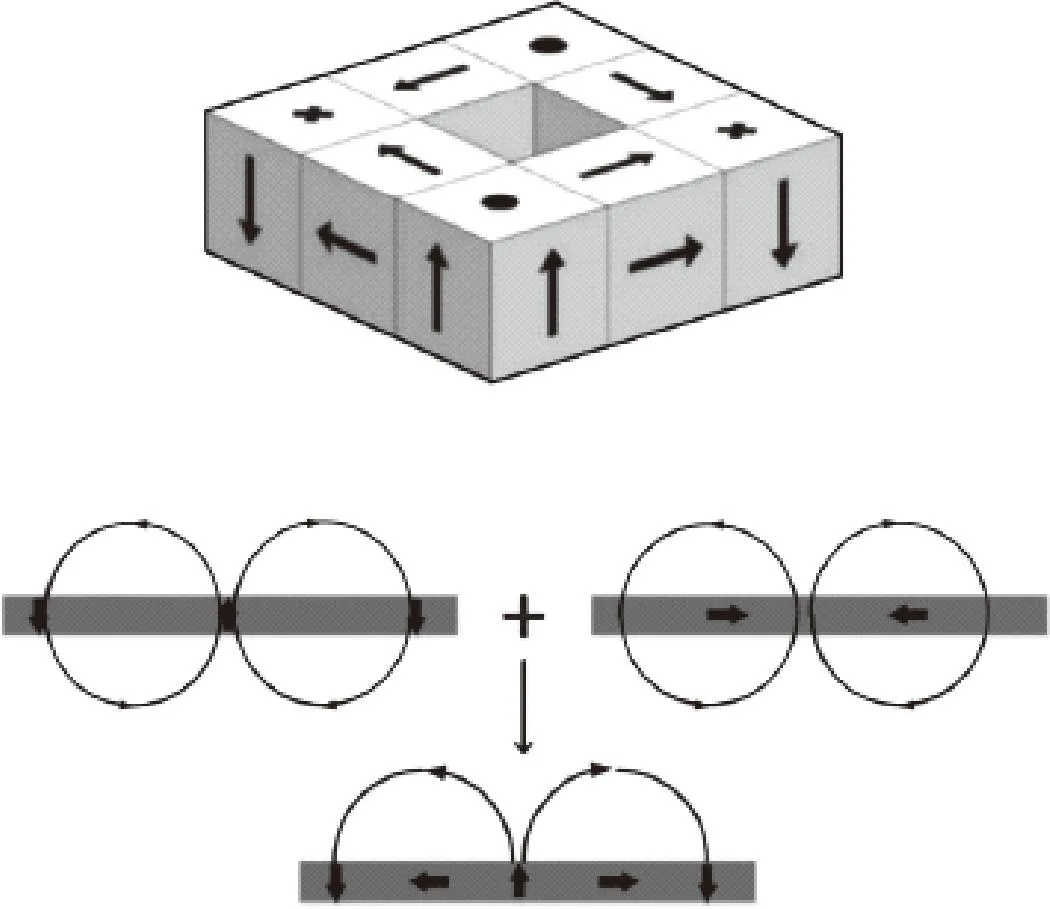
图1 Halbach阵列磁铁Fig.1 Halbach array magnet
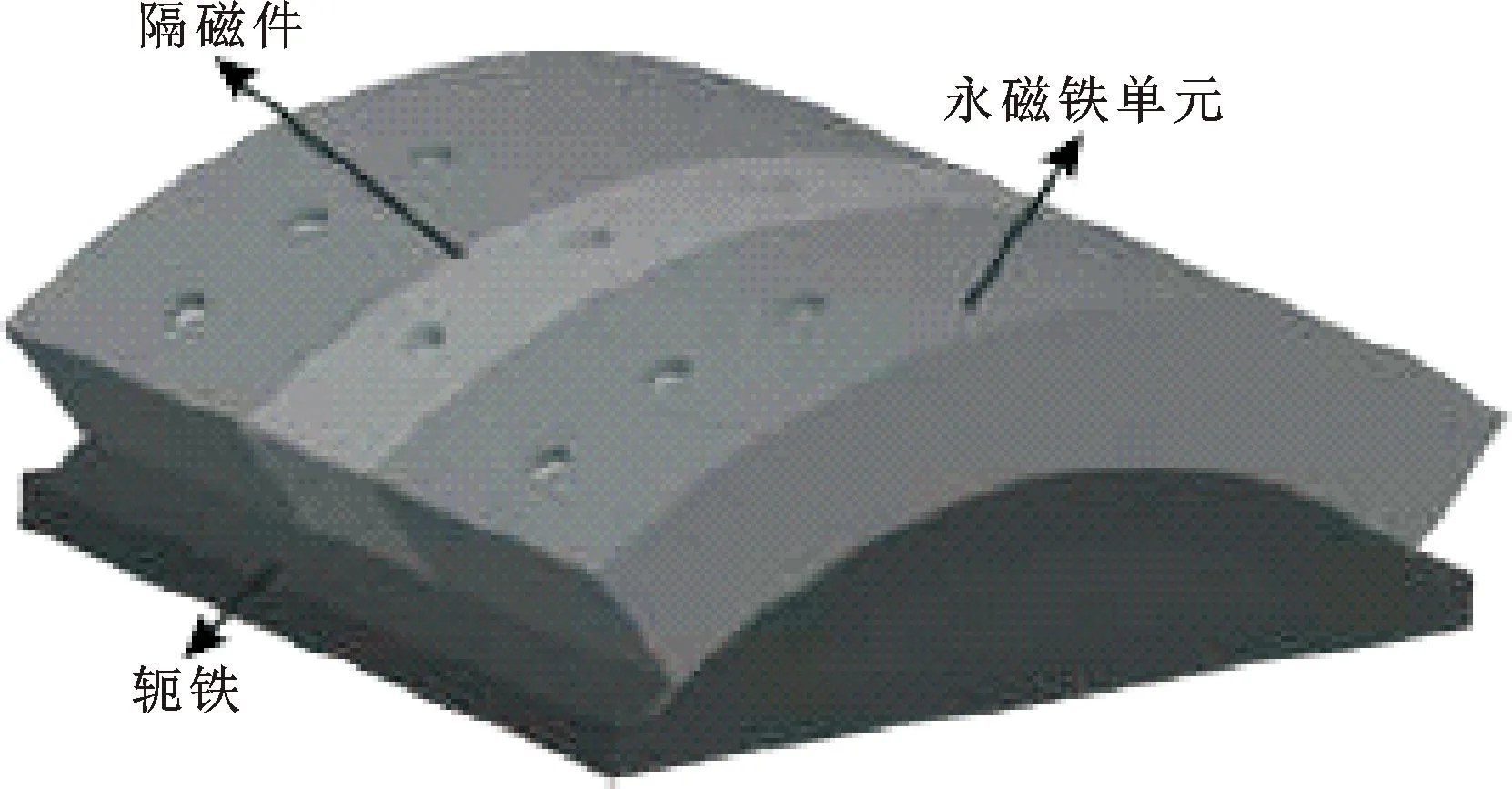
图2 磁吸附组件结构Fig.2 Struture of magnetic components
本文作者设计了一种适用于大负载轮式机器人的永磁吸附单元,即采用Halbach阵列磁路的瓦形磁吸单元。基于静态磁场理论、Maxwell仿真计算以及试验测试对比分析,对磁吸单元及其力学特性进行研究。引入磁质比和衰减率概念,定量分析了不同结构形式和磁路设计对其磁力性能的影响,为后续机器人总体设计提供参考。
1 静态磁场理论模型
基于Ansoft-Maxwell 软件,采用有限元仿真方法对3D静态磁场进行求解,求解方程有:麦克斯韦方程、边界条件和介质的本构方程。麦克斯韦方程组在3D静态磁场中的微分形式分为两部分,安培环路定律和磁路高斯定律[15]:
(1)
式中:H(x,y,z)为磁场强度;B(x,y,z)为磁感应强度;J(x,y,z)为电流密度。
磁场的边界条件包括磁场法向边界条件、磁场切向边界条件和齐次诺依曼边界条件,这3种边界条件分别对应公式(2)、(3)和(4)。
n×(B1-B2)=0
(2)
n×(H1-H2)=Js
(3)
(4)
式中:n为垂直边界面的外法线矢量;B1、B2为边界处两侧的磁感应强度;H1、H2为边界处两侧的磁场强度;Γ为诺依曼边界;f(Γ)、h(Γ)为常函数。
永磁单元的各种材料和船体外板都属于各向同性材料,故磁感应强度为
B=μ·H
(5)
μ=μ0·μr
(6)
式中:μ为导磁率;μ0为真空中的绝对磁导率,μ0=4π×10-7H/m;μr为相对磁导率。
由式(5)知,磁感应强度B散度为0,为方便分析,引入辅助矢量矩阵A,且A满足:
B=∇×A
(7)
矩阵A必须为唯一值,由库仑规范可知:
∇·B=0
(8)
由式(1)及式(5)-式(8)可得:
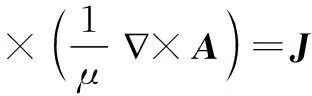
(9)
磁场分析的最终目的是算出吸附机构与壁面间的吸附力。根据Maxwell张力法,作用在壁面上的磁吸附力为
(10)
式中:T为张力张量;S为包围在磁场空间中的介质的闭合面;n为闭合面任意位置外法向方向的单位矢量;B为闭合面任意处的磁感应强度;μ为空气的相对磁导率。
上述理论模型是进行有限元磁场与磁力仿真计算的根本依据。由公式(10)可知,计算及分析磁力和磁场时,需要在封闭域内进行。
2 永磁吸附单元磁力试验分析
为验证仿真软件计算结果的可靠性,确保磁吸单元可以为轮式爬壁除锈机器人提供足够的吸附力,在合肥市稀土永磁材料国家重点实验室分析测试中心开展磁力试验,测试瓦形磁吸单元与钢板不同间距时的吸附力。瓦形磁吸单元的三维模型如图3所示,分为1、2和3号磁块。
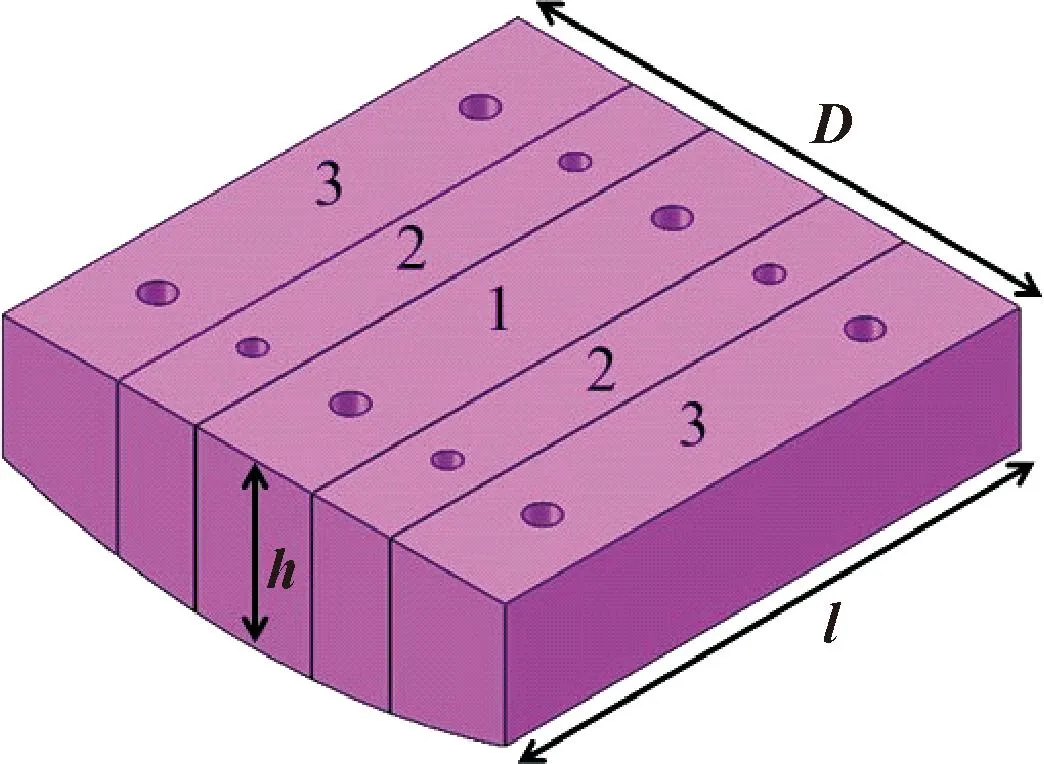
图3 瓦形磁吸单元模型Fig.3 Tile-shaped magnetic adsorption unit model
根据模型加工制作出瓦形磁吸单元的实物,在其上方放置一块钢板作为隔磁材料,下方固定一块钢板,用于模拟船体外部钢板,如图4所示。钕铁硼磁铁、背板和钢板的尺寸如表1所示。使用电子万能试验机作为吸附力测试试验设备,试验开始前,将瓦形磁吸单元与电子万能试验机的拉力传感器固结,试验现场如图5所示。
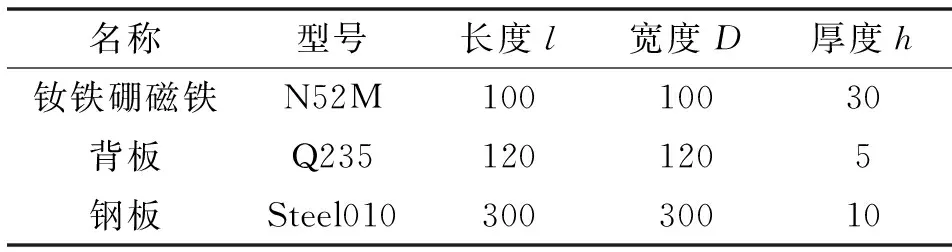
表1 试验材料尺寸 单位:mmTab.1 Test material sizes Unit:mm

图4 瓦形磁吸单元实物Fig.4 Tile-shaped magnetic adsorption unit entity

图5 试验现场Fig.5 Testing site
采用准静态试验法,磁吸单元在微机控制下以1 mm/min速度缓慢向上移动,直至瓦形磁吸单元离开钢板1.6 mm。上升距离即为瓦形磁吸单元与钢板之间的间距d。记录磁吸单元吸附力大小F,得到吸附力与间距的关系,并与软件仿真计算结果进行对比,得出仿真相对于试验的误差ε,如图6所示。误差ε的定义为
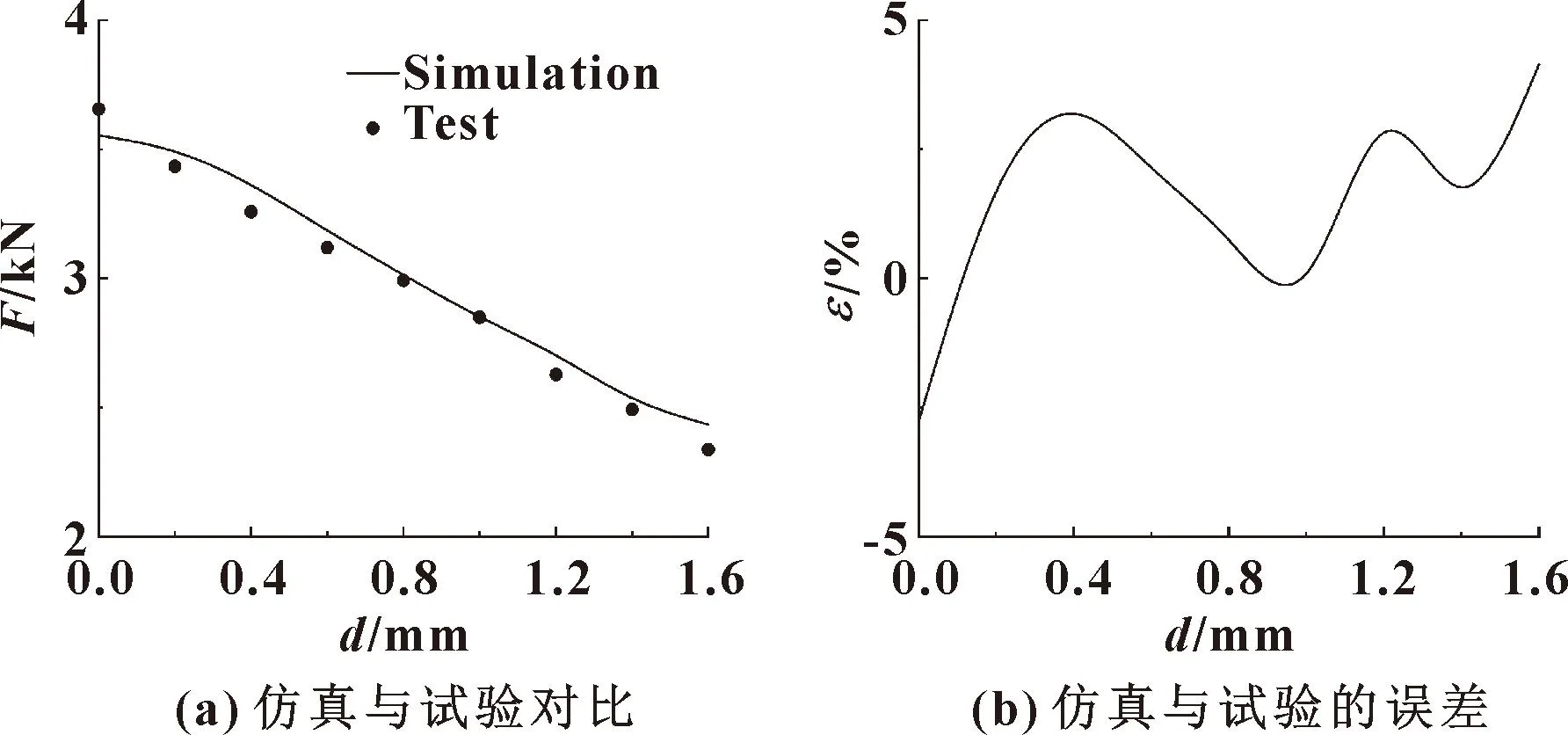
图6 瓦形磁吸单元的磁力与间距关系Fig.6 Relationship between magnetic force and spacing of tile-shaped magnetic adsorption unit:(a)comparison of simulation and test;(b)errors of simulation and test
(11)
式中:F1是仿真值;F2是试验值。
从图6(a)可以看出,试验测得的磁力分布在仿真结果曲线的上下两侧;从图6(b)中可以看出,间距0~1.6 mm时,仿真相对于试验的误差小于5%。表明:Ansoft-Maxwell软件的仿真计算结果是可信的。
3 仿真计算结果对比分析
3.1 仿真计算模型与过程
为了增强轮式爬壁机器人吸附单元的吸附力,设计了新型的磁吸单元结构与磁路,分别为A型、B型和C型,如图7所示。A型与B型相比优化了磁路,由常规配对磁路改进为Halbach阵列磁路;A型、B型与C型相比,设计了新型的瓦形结构。将图7中3种磁吸单元的3D模型导入Ansoft-Maxwell磁力仿真软件,依次经过选择静态磁场求解器,补充建立背板、钢板和求解域模型,设置材料属性,设置边界条件,设置求解参数和网格划分,最后进行有限元计算,得到仿真磁力结果。A型、B型和C型磁吸单元的求解模型及求解域如图8所示。

图7 磁吸单元结构与磁路Fig.7 Magnetic adsorption unit structure and magnetic circuit:(a)A type;(b)B type;(c)C type
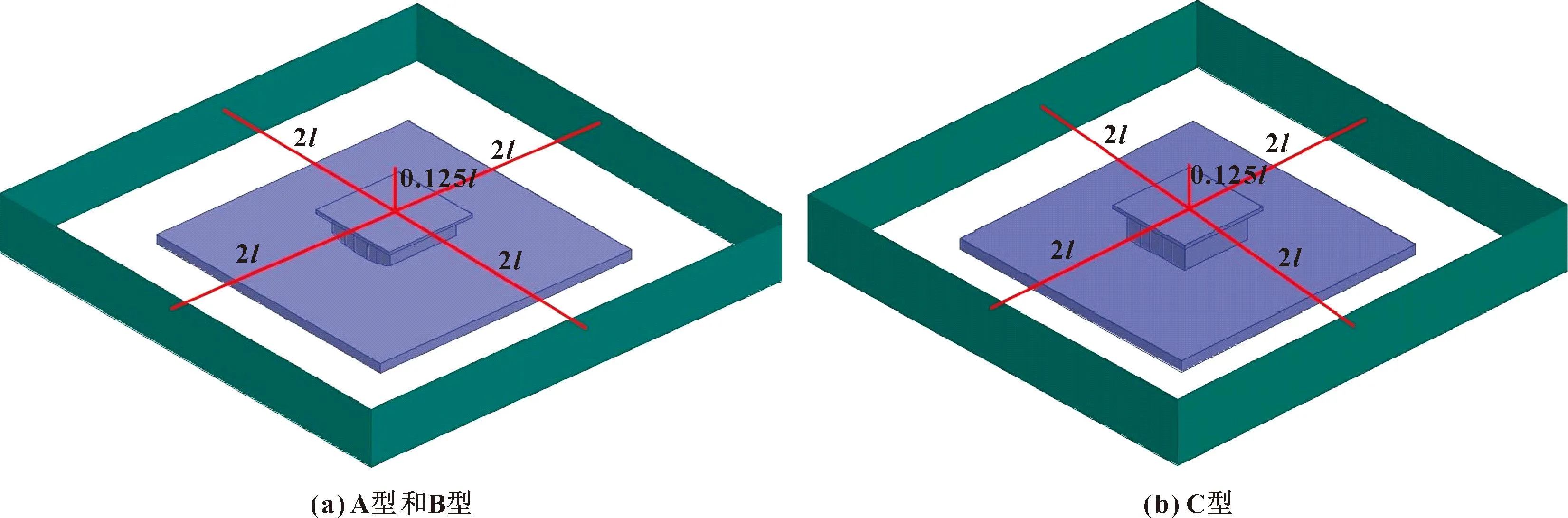
图8 模型和求解域Fig.8 Models and solution domains:(a)A type and B type;(b)C type
以A型磁吸单元(间距2 mm)为例,进行网格收敛性验证。如图9所示:网格总数大于42万之后,随着网格增加,磁力增大幅度小于0.1%,表明仿真计算的磁力结果已经收敛。为了平衡计算速度和计算精度,将网格设置为约42万。网格划分如图10所示,计算域内网格数为33.8万,磁瓦中网格数为4.6万,背板中网格数为0.9万,钢板中网格数为2.7万。
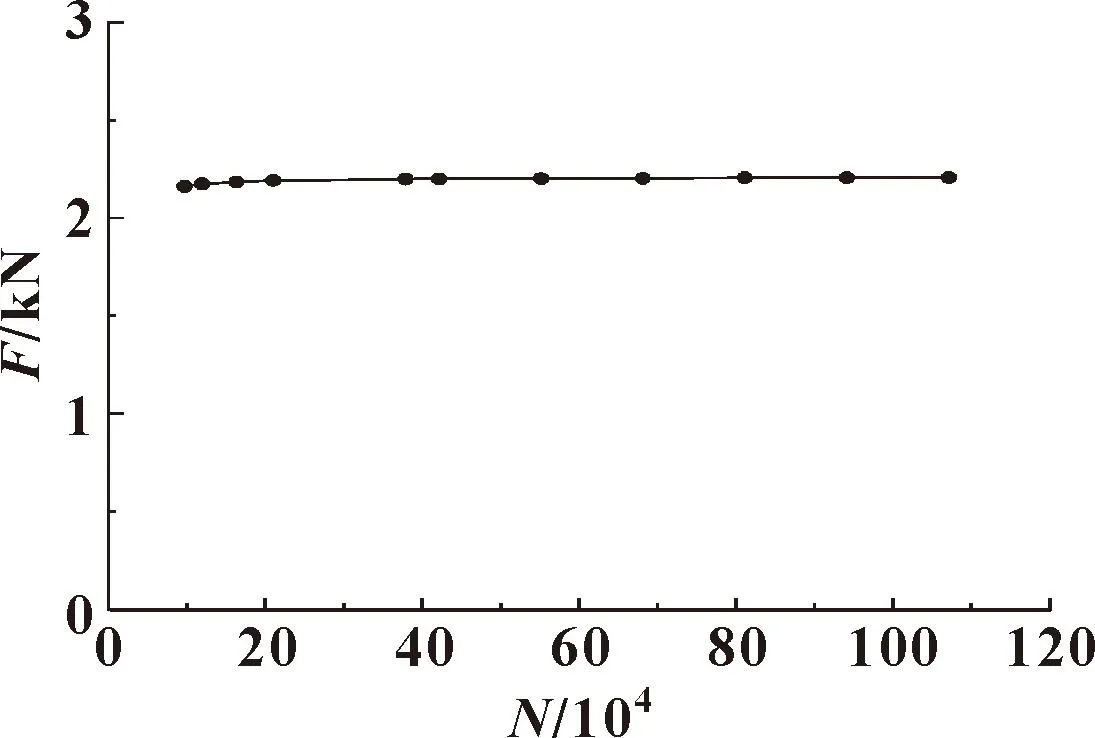
图9 网格收敛性验证Fig.9 Verification of mesh convergence

图10 网格划分图Fig.10 Meshing diagram
3.2 磁力计算结果分析
研究磁力与磁吸单元和钢板间距的关系,对比分析A型、B型和C型3种磁吸单元的磁力大小,以及磁力对距离变化的敏感程度。选取磁吸单元与钢板间距0~4 mm进行仿真,得到3种磁吸单元的磁力F与间距d的变化关系,将磁力进行归一化处理,如图11所示。归一化处理即求得不同间距处的磁力与最大磁力的比值,定义为
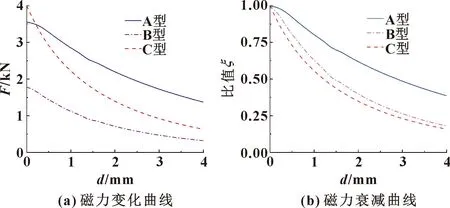
图11 不同磁吸单元磁力与间距关系Fig.11 Relationship between magnetic force and distance of different magnetic adsorption units:(a)magnetic force change curves;(b)magnetic force decay curves
ξ=Fi/Fmax
(12)
式中:ξ为比值;Fi为不同间距的磁力;Fmax为最大磁力。
由图11(a)可以看出:(1)A型吸附单元与C型吸附单元的变化曲线趋势基本一致,而磁力是两倍关系,表明Halbach阵列磁路极大地增加了磁力;(2)间距0~0.2 mm时,C型磁吸单元的磁力大于A型磁吸单元的磁力,间距0.2~4 mm时,A型磁吸单元的磁力大于C型磁吸单元的磁力。因为C型磁吸单元比A型磁吸单元多出了两侧的部分,而间距对磁力影响较大,两侧的部分提供更大的磁力。
由图11(b)可以看出:(1)B型和C型磁吸单元磁力衰减曲线趋势一致;(2)相较于B型和C型磁吸单元,A型磁吸单元对距离变化不敏感,随间距增加,A型磁吸单元磁力衰减速度慢,衰减率是其0.5倍。
引入磁质比γ的概念,表征磁力与磁吸单元质量的比值,定义为
(13)
式中:F为磁力;m为磁吸单元质量。
轮式机器人的磁吸单元与钢板间距的设计值定为1.6 mm,计算此时A型、B型和C型磁吸单元的磁质比,如表2所示。可知:(1)通过A型与B型磁吸单元的对比,可以看出,Halbach阵列磁路极大地增加了磁铁的磁质比,Halbach阵列磁路的磁质比是常规配对磁路的2.87倍;(2)通过A型与C型磁铁的对比,可以看出,A型磁铁比C型磁铁质量小,仍因为使用Halbach阵列充磁方式,使得A型磁吸单元磁质比更大。
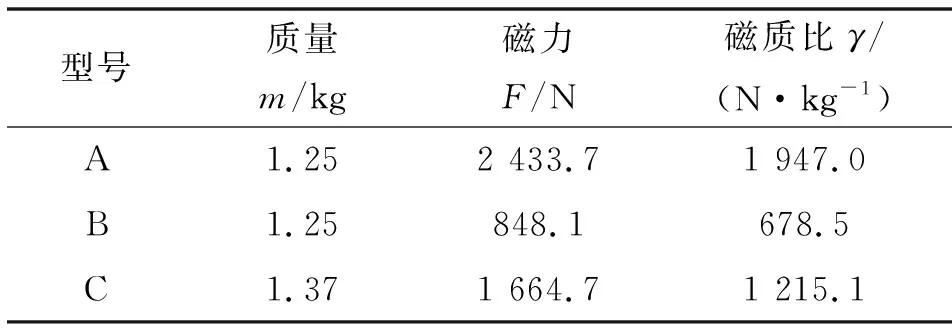
表2 磁质比Tab.2 Magnetic mass ratio
3.3 磁场强度分析
通过试验测量瓦形磁吸单元底部磁感应强度,与仿真结果对比,如图12所示。可以看出:试验与仿真测得的磁感应强度曲线变化趋势一致,误差小于10%;由于瓦形磁吸单元采用Halbach阵列磁路,导致1号磁块表面磁感应强度不同,将2号磁块的磁场汇集到1号磁铁处。
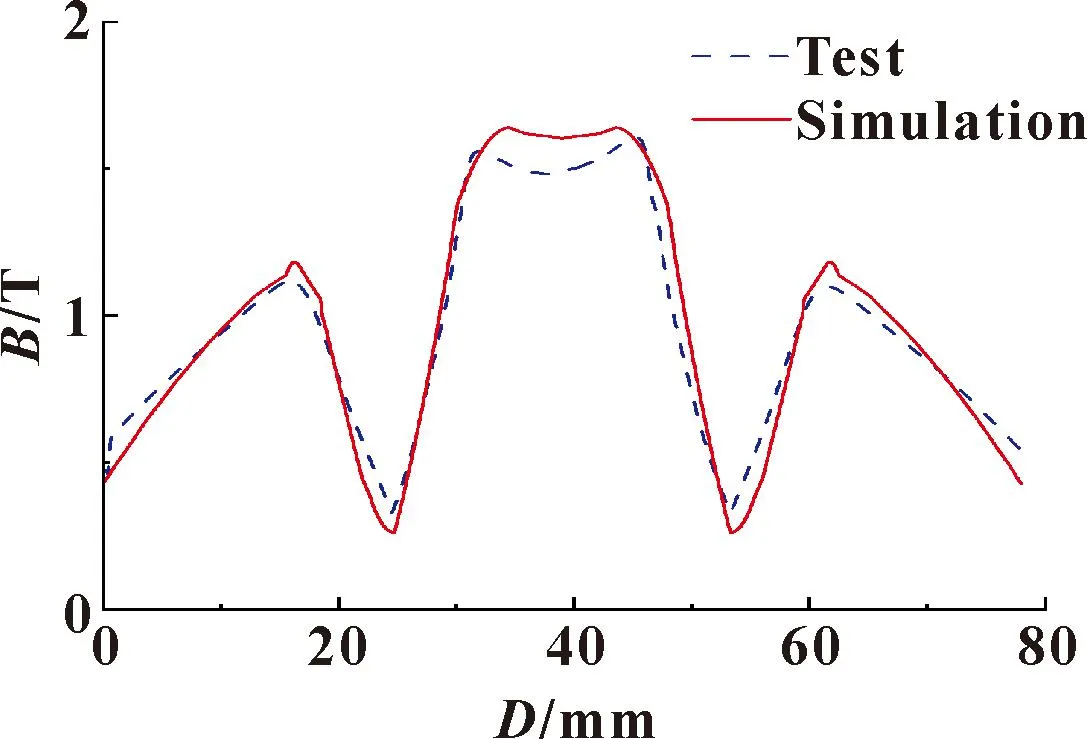
图12 试验与仿真对比Fig.12 Comparison of test and simulation
通过Ansoft-Maxwell软件对比分析A型、B型和C型磁吸单元底部(即靠近钢板一侧)沿磁吸单元宽度的磁感应强度,见图13。可以看出:Halbach充磁方式减弱了2号磁块下表面的磁感应强度,增强了1号磁块下表面的磁感应强度。1号磁块距离钢板近,2号磁块距离钢板远,而磁吸单元的磁力随间距增大而减小,间距增大后,主要依靠1号磁块提供吸附力,因此Halbach阵列磁路能够增大磁力。

图13 底部磁场强度Fig.13 Magnetic field strength at the bottom
A型、B型和C型磁吸单元中剖面的磁感线分布如图14所示,可以看出:Halbach阵列充磁方式优化了磁路,降低了异性磁极间的磁场损耗。
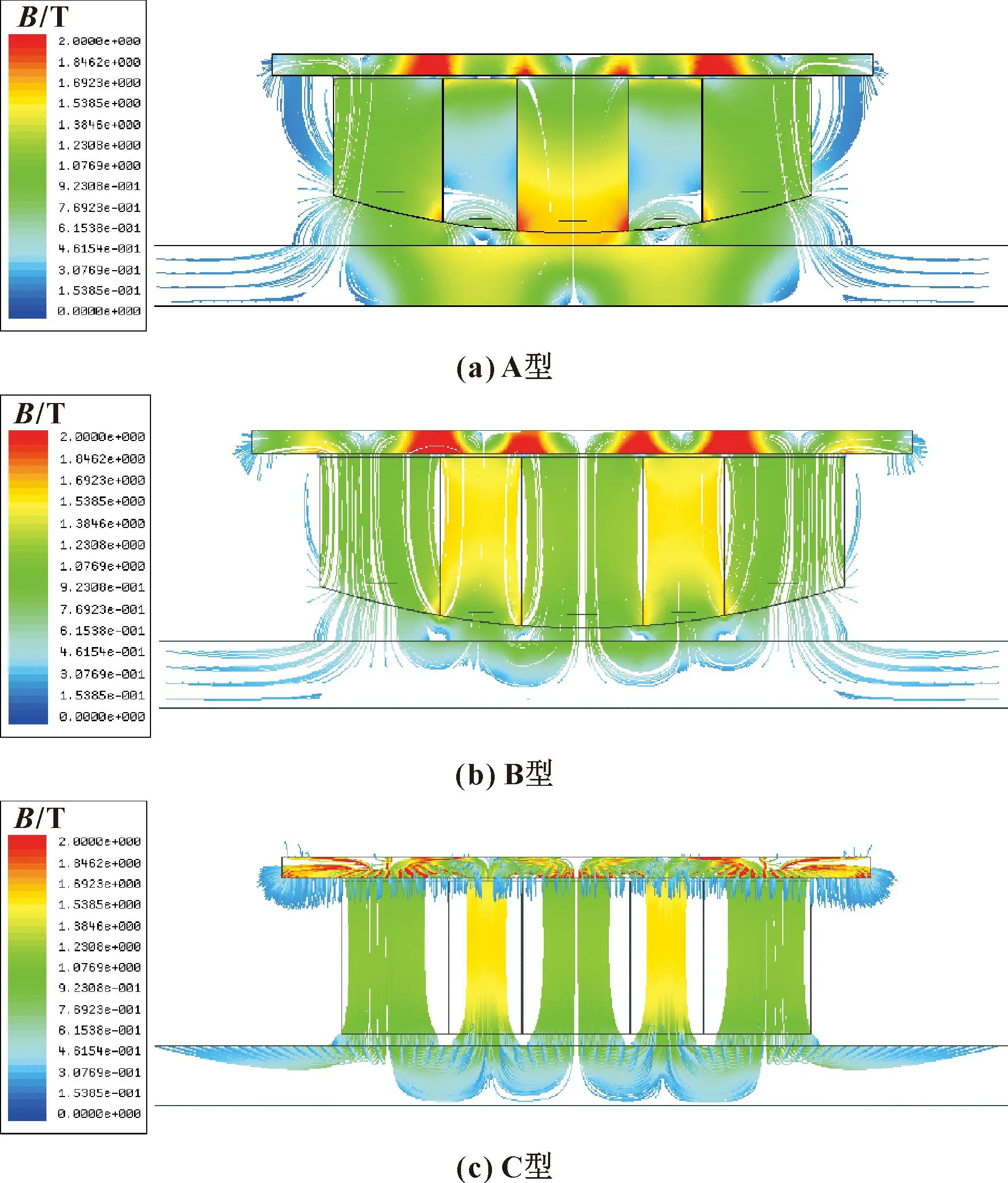
图14 磁感线分布Fig.14 Magnetic induction line distribution:(a)A type; (b)B type;(c)C type
4 结论
基于静态磁场理论、Maxwell仿真和试验,完成了A型、B型和C型3种磁吸单元与钢板不同间距时的磁力分析,3种磁吸单元的磁质比计算,以及磁铁上、下侧的磁感应强度计算域分析,得出以下结论:
(1)通过磁吸单元的试验测试,验证了Ansoft-Maxwell软件仿真计算磁力的准确性,磁力计算误差小于5%,磁场分布计算最大误差小于10%。
(2)Halbach阵列磁路增大磁吸单元磁质比,降低对距离的敏感性;Halbach阵列磁路的磁质比是常规配对磁路的2.87倍,衰减率是其0.5倍。
(3)Halbach阵列瓦形磁吸单元优化了磁路,减弱了异性磁极间的磁场损耗,使得磁吸单元表面磁感应强度增强。
