变刚度弹簧对高压大流量安全阀响应特性的影响规律

侯文龙，廉自生，2，郭永昌，2

(1.太原理工大学机械与运载工程学院，山西太原 030024；2.太原理工大学煤矿综采装备山西省重点实验室，山西太原 030024)

0 前言

液压支架是煤矿机械化综采工作面的核心设备之一，安全阀是液压支架重要的安全保护元件，也是液压支架最容易损坏的元件之一。安全阀对支架主要起过载保护的作用，在顶板来压时及时卸荷，避免支架立柱压弯、爆裂及顶梁和底座等焊接构件开焊、断裂等事故的发生，保护井下工人的生命安全。因此，在有冲击地压和坚硬难冒落的特殊顶板条件下，安全阀动态性能的优劣直接影响到液压支架支护性能的发挥[1]。

随着综采技术和综采装备的发展，液压支架的支护高度、支护强度、承载能力不断提高，液压支架的最大支护高度已达9.2 m，工作阻力达到29 000 kN[2]，立柱直径也越来越大，对安全阀的性能提出了更高的要求，1 000 L/min及以上的高压大流量安全阀的需求越来越高，具体为：(1 )工作压力高，公称压力在40～55 MPa之间；(2)溢流能力强，公称流量不小于1 000 L/min。

杨帅鹏[3]以直动式安全阀为研究对象，在AMESim中对不同弹簧刚度、溢流孔、搭合量、溢流孔径等结构参数进行仿真，分析其对安全阀动态特性的影响，确定最佳的参数设置方案。高宇龙等[4]以双级安全阀为研究对象，分析了不同阀芯直径对其开启特性及流量特性的影响。权宁、李荣兵[5]利用Simulink分析了大流量安全阀弹簧刚度等结构参数对其动态特性的影响。陈明亮等[6]设计了双排阀口和并联式双弹簧结构的安全阀，能够减小阀腔内负压，抑制气穴形成，改善抗气蚀性能。

本文作者以典型的1 000 L/min直动式安全阀为研究对象，建立数学模型和AMESim仿真模型，以弹簧作为切入点，分析定刚度弹簧和变刚度弹簧对冲击载荷下安全阀动态响应特性的影响；此外，还设计一种以氮气为气体弹簧的新结构安全阀，以提高高压大流量安全阀的稳定性和可靠性，为高压大流量安全阀的设计提供理论基础。

1 高压大流量安全阀的结构及工作原理

1.1 安全阀结构

典型1 000 L/min直动式安全阀的结构如图1所示。公称压力为42～55 MPa，公称流量为1 000 L/min。

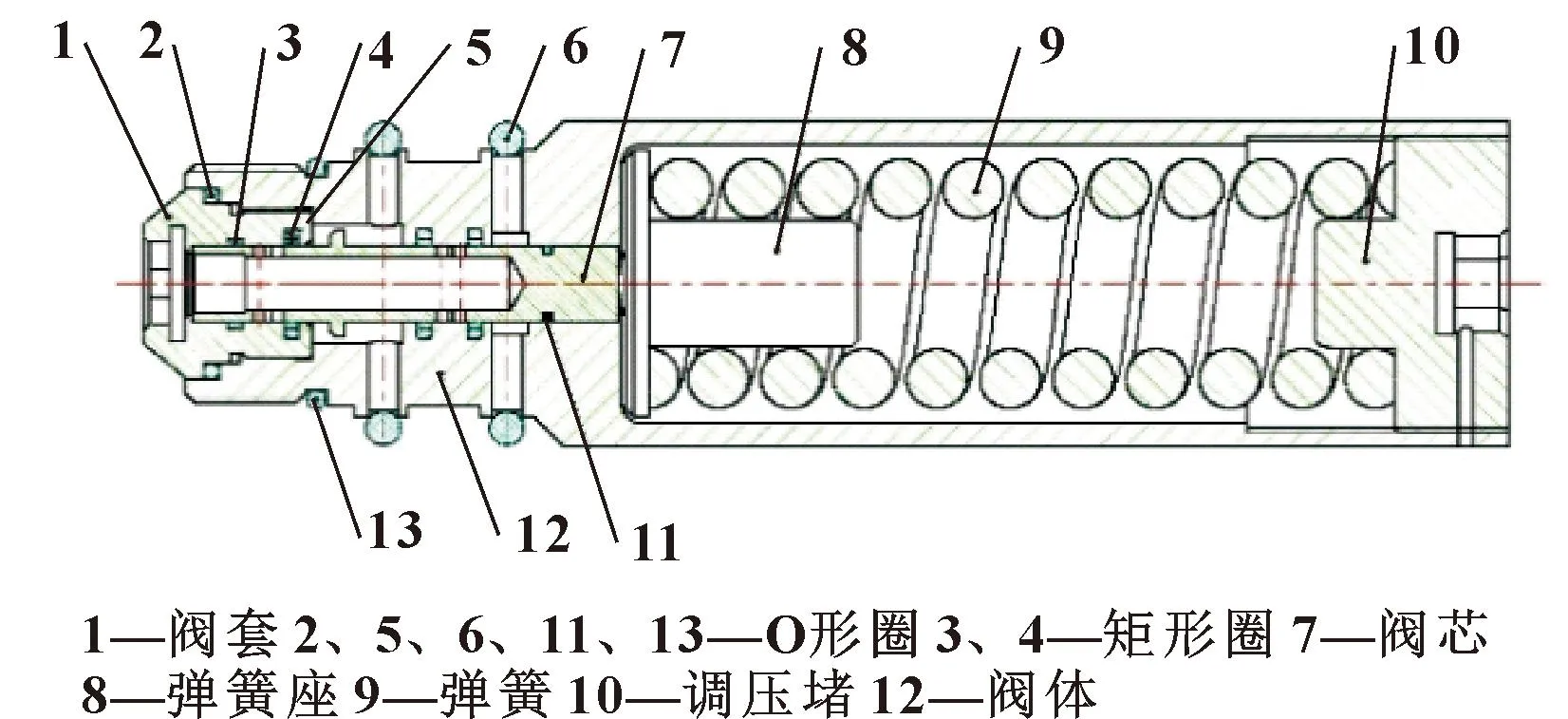
图1 1 000 L/min直动式安全阀结构Fig.1 1 000 L/min direct-acting safety valve structure

1.2 安全阀工作原理

直动式安全阀中作用在阀芯7上的液压力和作用在弹簧座8上面的弹簧力相互作用控制阀芯7的开启和关闭。支架受到顶板的冲击力时，安全阀的阀前压力会升高，当阀芯上的液压力大于弹簧力时，阀芯右移，阀芯上的溢流孔打开，安全阀开始溢流，阀前压力下降；当液压力小于弹簧力时，阀芯左移，阀芯溢流孔关闭，安全阀停止溢流。

2 高压大流量安全阀的数学模型

(1)阀口流量方程

(1)

式中：Cd为流量系数，Cd=0.65；A1为瞬时有效通流面积，mm2；p1为安全阀入口压力，MPa；p0为安全阀出口压力，MPa；γ为5%乳化液的重度，γ=9 800 N/m3。

由安全阀的结构可知(图2)，在溢流过程中，溢流孔出口通流面积随阀芯运动而逐渐变化，因此，阀口开度x与通流面积A1的关系[7]为

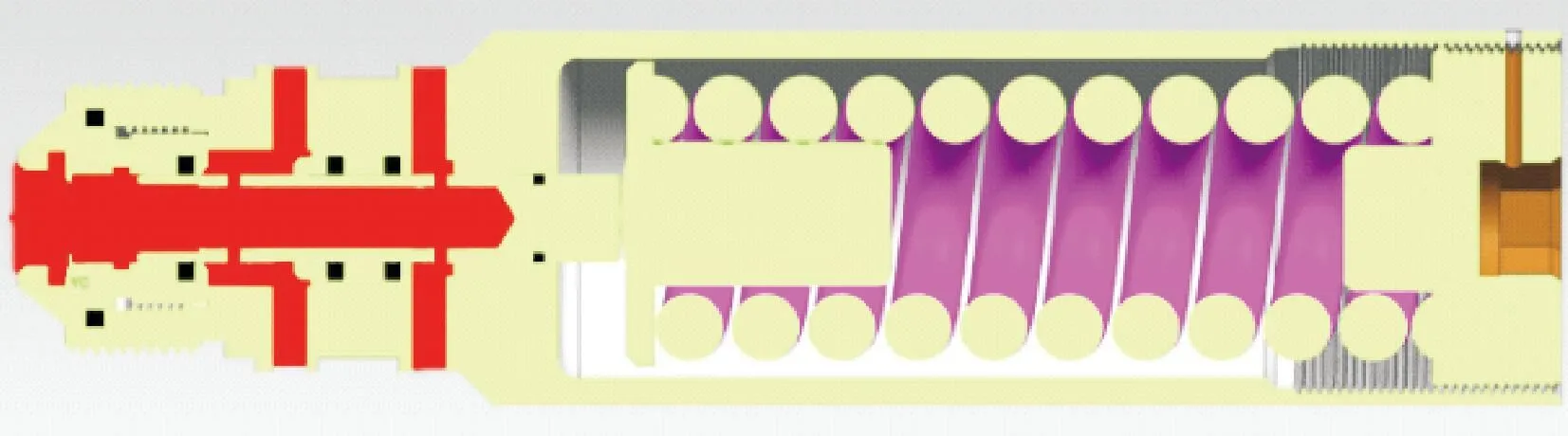
图2 安全阀完全开启时流道示意Fig.2 Schematic of the flow path when the safety valve is fully opened

A1=n[π/180arccos(1-x/R)R2-

(2)

A1=n[πR2-π/180arccos(x/R-1)R2-

(3)

式中：n为溢流孔数量；R为阀芯溢流孔半径，mm。

(2)流量连续性方程

(4)

式中：Qs为等效流入安全阀的流量，L/min；A为安全阀入口面积，m2；Ve为管路及安全阀前腔的液体容积，m3；βe为工作介质的体积弹性模量，N/m2；Ct为泄漏系数。

(3)阀芯运动微分方程

对运动中的安全阀阀芯进行受力分析，得其运动微分方程：

(5)

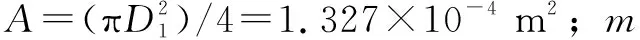
(4)稳态液动力

稳态液动力可按轴向和径向分解为轴向分量和径向分量，通常它在安全阀流道是轴对称的，因此稳态液动力的径向分量就可以相互抵消掉，只有轴向液动力对大流量安全阀产生影响。轴向稳态液动力的计算公式为

FZS=2CdCvπdxΔpcosα

(6)

式中：Cd为流量系数，Cd=0.65；Cv为速度系数，Cv=0.98；d为安全阀溢流孔直径，mm；x为阀口开度，mm；Δp为密封圈前后压差，MPa；α为阀口液流角，(°)。

(5)安全阀密封圈摩擦力

通过查阅《液压阀设计手册》可以得出，单个O形密封圈作用在阀芯上的摩擦阻力为

FZM=f1N=1/3f1πΔpD1d0

(7)

式中：f1为O形密封圈与阀芯之间的摩擦因数，取f1=0.1；D1为安全阀阀芯外径，mm；d0为密封圈断面直径，mm。

由上述的数学表达式可以看出：大流量安全阀的设计参数包括弹簧刚度、阀芯质量、溢流孔数量和直径等都会对其动态特性产生影响。

对式(4)(5)进行拉氏变换得式(8)(9)。根据公式(1)(8)(9)在MATLAB/Simulink中建立基于安全阀数学模型的方框图[8]，参数设置如表1所示，方框图如图3所示。

表1 1 000 L/min直动式安全阀的结构参数Tab.1 Structural parameters of 1 000 L/min direct-acting safety valve

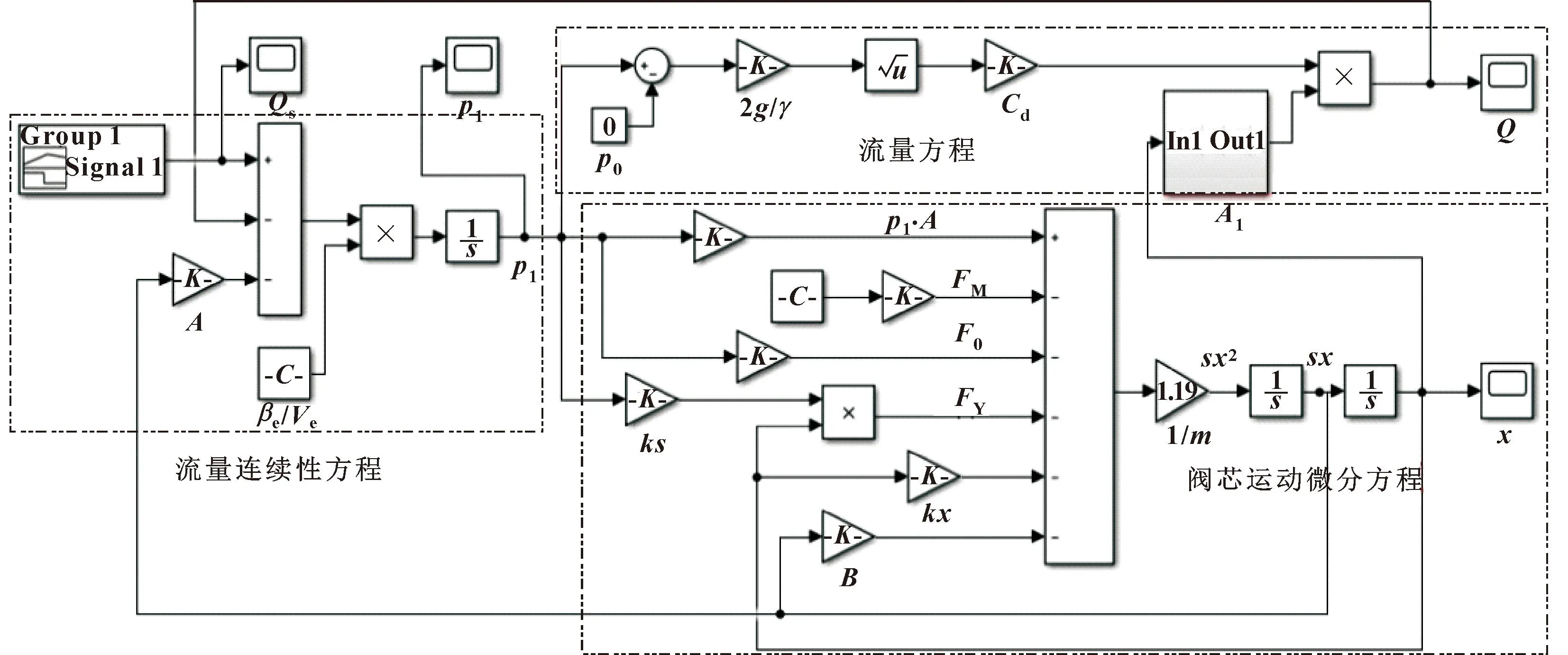
图3 直动式安全阀动态仿真模型Fig.3 Dynamic simulation model of a direct-acting safety valve

Qs-Q=Asx+Ve/βesp1+Ctp1

(8)

p1A=ms2x+k(x0+x)+Bsx+FZM+FZS

(9)

给定立柱下腔流出的瞬时流量为1 000 L/min时，安全阀动态仿真的压力、阀芯位移及流量曲线如图4所示。由图4(a)可知：安全阀前腔的峰值压力为64.4 MPa，峰值压力时间20 ms，稳定后液压缸下腔压力为55.0 MPa，开启延迟时间为8 ms，压力稳定时间51 ms，阀芯最大开度为6.7 mm，稳定后位移5.5 mm。安全阀关闭后液压缸下腔压力保持在40.6 MPa。由图4(b)可知：安全阀卸荷时瞬时流量最大可达1 110 L/min，稳定卸荷时流量为1 000 L/min。

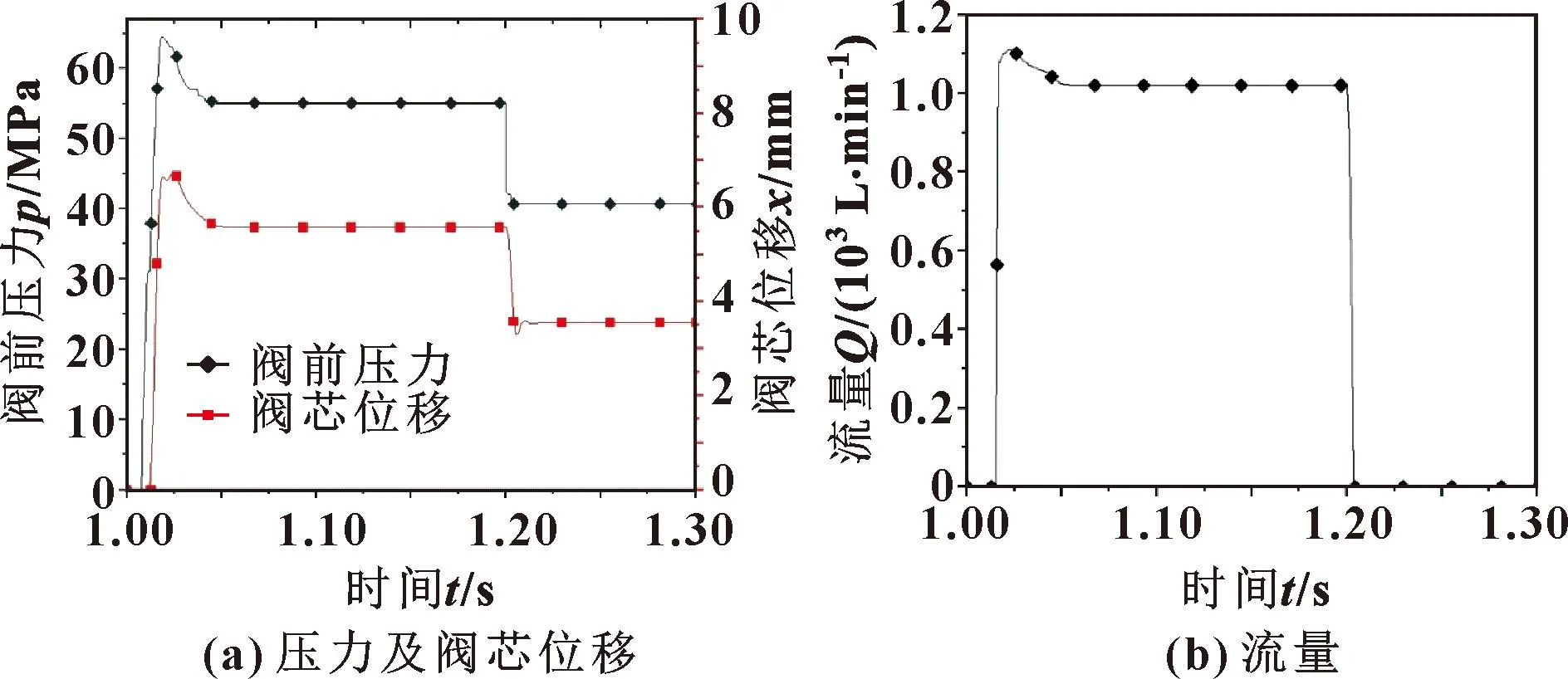
图4 安全阀动态特性仿真分析曲线Fig.4 Simulation analysis curves of safety valve dynamic characteristics：(a)pressure and spool displacement；(b)flow rate

3 AMESim仿真与分析

3.1 高压大流量安全阀

使用AMESim中的HCD元件库进行大流量安全阀的仿真模型搭建，参照1 000 L/min直动式安全阀的结构建立如图5所示的仿真模型[9]，参数设置如表1所示。

图5 AMESim中的1 000 L/min直动式安全阀Fig.5 1 000 L/min direct-acting safety valve in AMESim

3.2 加载试验系统

高压大流量安全阀加载试验原理如图6所示，根据实验原理搭建如图7所示的AMESim安全阀液压系统仿真模型。将表1中安全阀的参数输入模型中，并设置加载试验系统的仿真参数如表2所示。

表2 安全阀试验加载系统参数设置Tab.2 Parameters of loading system for safety valve test

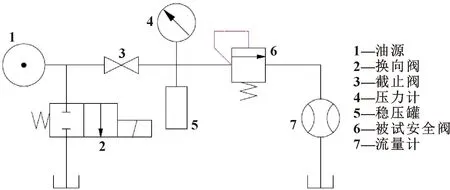
图6 安全阀试验原理Fig.6 Principle of safety valve test

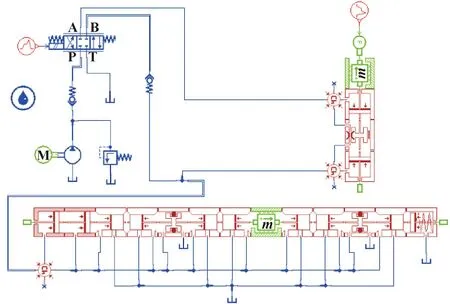
图7 安全阀加载试验仿真模型Fig.7 Simulation model of the safety valve loading test

设置仿真时间为15 s，步长为0.001 s，在10 s时模拟顶板来压(图8)，得到直动式安全阀的性能曲线如图9所示。可知：直动式安全阀在冲击压力下的峰值压力为61.7 MPa，峰值时间8.4 ms，压力超调量为11.7 MPa，超调率23.4%，开启延迟时间4.6 ms，压力稳定时间75.3 ms。通过比较Simulink和AMESim仿真曲线，二者压力超调量和阀芯位移曲线近似，验证了模型的正确性。

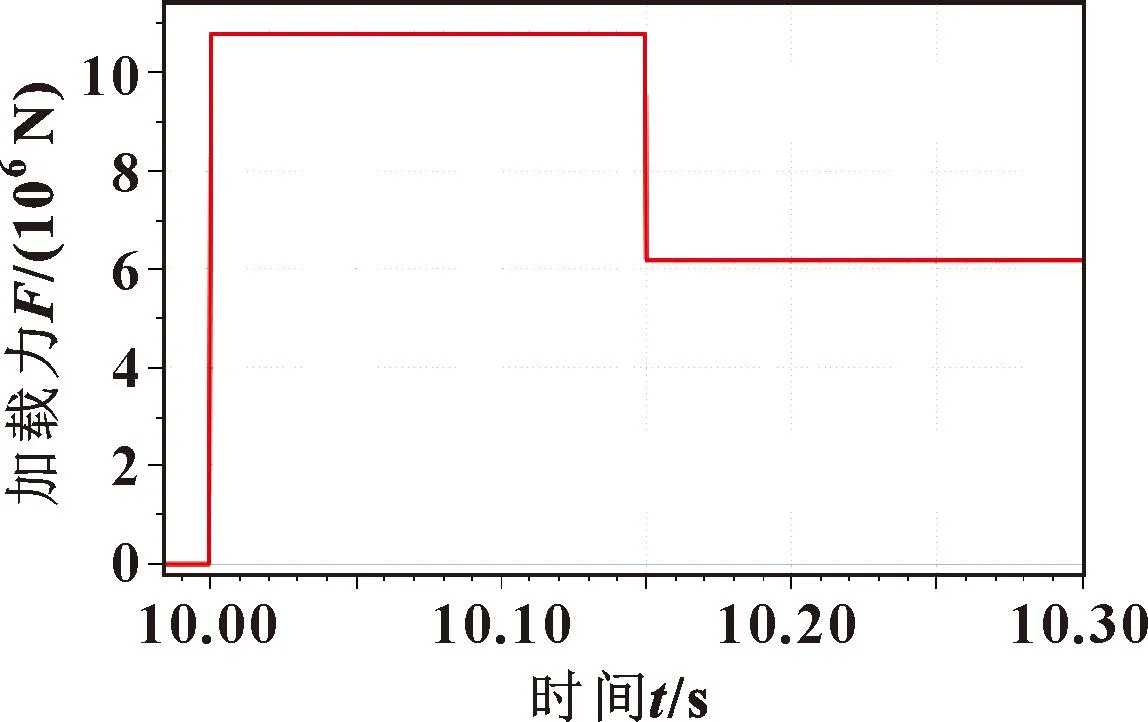
图8 液压缸加载力Fig.8 Loading force of hydraulic cylinder

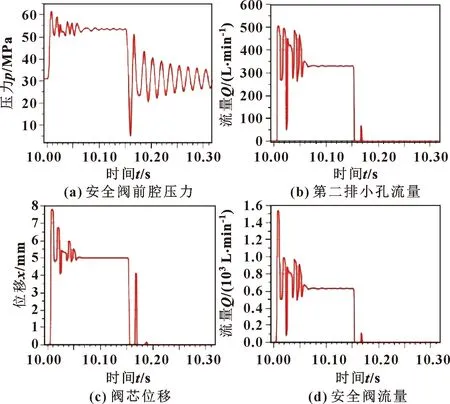
图9 直动式安全阀性能曲线Fig.9 Performance curves of direct-acting safety valves：(a) safety valve front chamber pressure；(b)second row of small hole flow rate；(c)spool displacement； (d)safety valve flow rate

3.3 定刚度弹簧刚度对安全阀响应特性的影响

为研究弹簧刚度对大流量安全阀响应特性的影响，将弹簧分为定刚度弹簧和变刚度弹簧2种，分别分析不同种类弹簧的优越性。

保持其他参数不变，弹簧刚度分别取285、334.8、385 N/mm，不同定刚度弹簧的特性曲线如图10所示，代入仿真模型得到的结果曲线如图11所示。

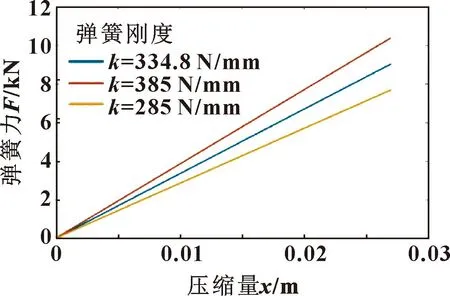
图10 不同定刚度弹簧的特性曲线Fig.10 Characteristic curves for springs of different constant stiffness

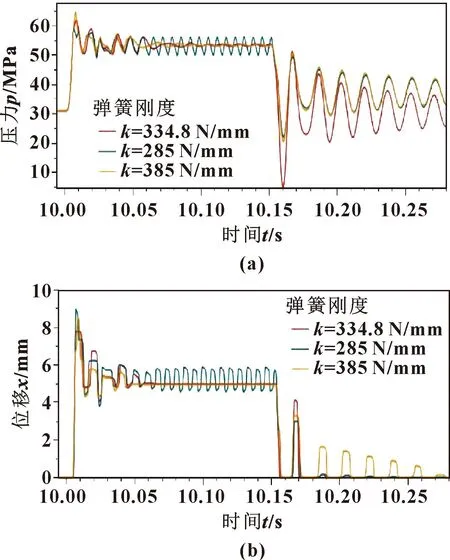
图11 三种弹簧刚度下的安全阀压力(a)和阀芯位移(b)曲线Fig.11 Pressure (a)and spool displacement (b)curves of safety valve under three kinds of spring stiffness

由图11可知：安全阀开启溢流时间段内，当弹簧刚度为285 N/mm时，安全阀的峰值压力为59.5 MPa，相比之下超调量有所降低，但压力不能趋于稳定，波动较大；当弹簧刚度为385 N/mm时，安全阀的峰值压力为64.8 MPa，超调量从11.7 MPa增加到了14.8 MPa，不利于安全阀及时卸荷。

3.4 变刚度弹簧刚度对安全阀响应特性的影响

MATLAB中利用曲线拟合工具箱(图12)，在给定的参数点下，拟合符合条件的变刚度弹簧[10-12]力-位移曲线。为减小阀芯在开启过程中弹簧的作用力及阀芯开启卸荷的响应时间，拟合如图13所示的F2N、F3N两条曲线，曲线表达式分别为f2(x)、f3(x)，原定刚度弹簧特性表达式设为f1(x)。将拟合曲线的表达式输入仿真模型中，运行仿真可得如图14所示的动态特性曲线。

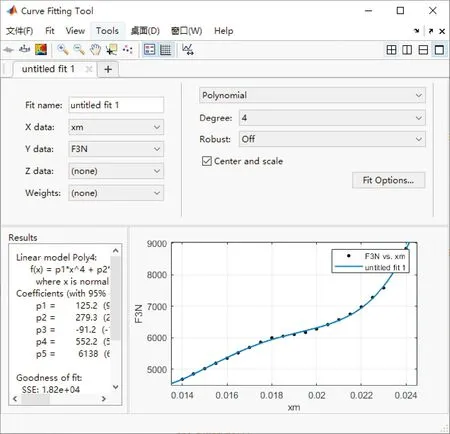
图12 MATLAB曲线拟合工具箱Fig.12 MATLAB curves fitting toolbox

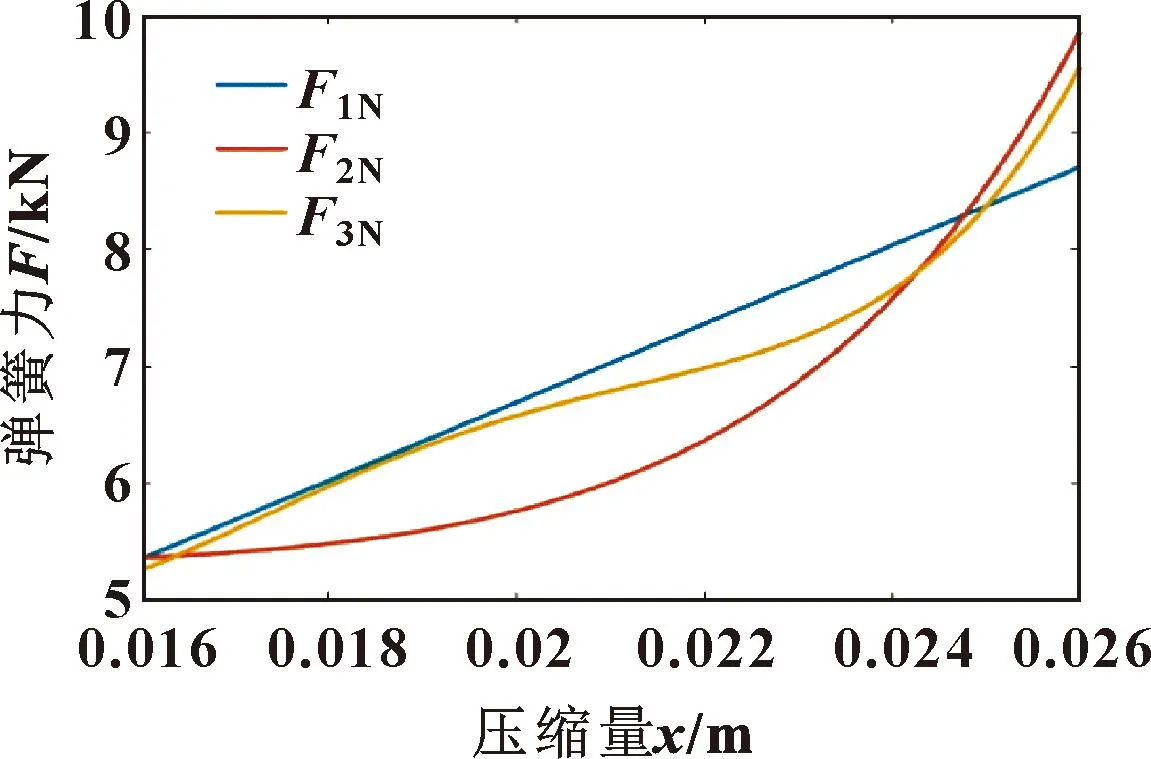
图13 变刚度弹簧特性曲线Fig.13 Characteristic curves of variable stiffness springs

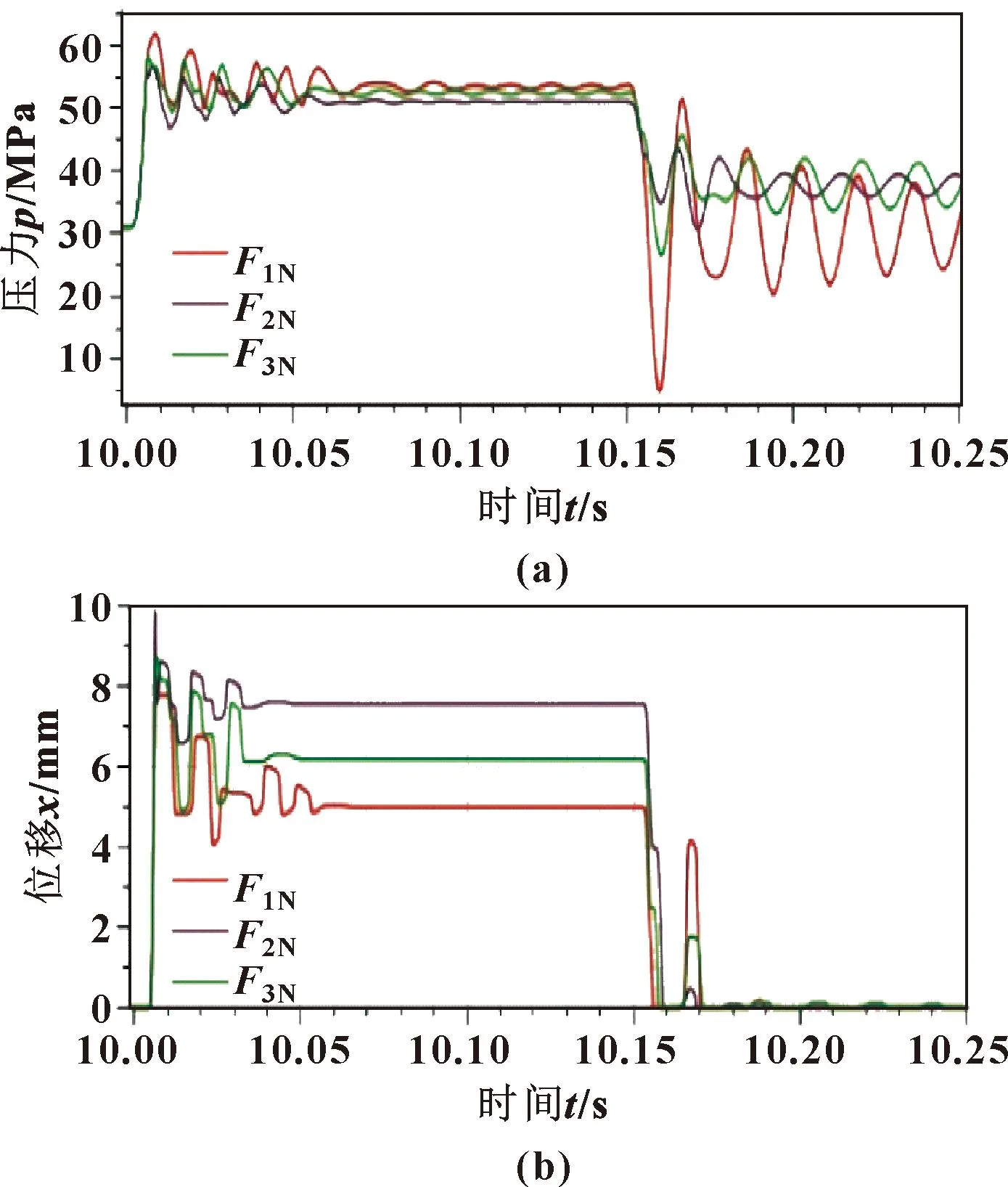
图14 变刚度弹簧压力(a)和阀芯位移(b)曲线Fig.14 Pressure (a)and spool displacement(b)curves of variable stiffness springs

f1(x)=334.8×103x

(10)

f2(x)=4.371×1014x5-4.323×1013x4+1.702×

1012x3-3.332×1010x2+3.243×108x-1.25×106

(11)

f3(x)=1.378×1012x4-1.063×1011x3+3.041×

109x2-3.794×107x+1.789×105

(12)

由图14可知：安全阀开启溢流期间，与原曲线相比，变刚度弹簧F2N的峰值压力最小，为56.8 MPa，超调量仅为6.8 MPa，F3N次之，峰值压力为58.2 MPa，超调量为8.2 MPa，F1N峰值压力最大；压力稳定时间也是F2N最小，为54.3 ms，F3N次之，为57 ms，F1N最大；开启延迟时间几乎不变，均为4.5 ms。

安全阀结束溢流时间段内，当安全阀阀芯位移恢复为0时，曲线F1N液压缸内压力为35.62 MPa，关闭时间为10.156 s，关闭延迟时间为60 ms；曲线F2N液压缸内压力为32.68 MPa，关闭时间为10.159 s，关闭延迟时间为91 ms；曲线F3N液压缸内压力为36.81 MPa，关闭时间为10.157 s，关闭延迟时间为77 ms。经过对比，定刚度弹簧F1N的关闭延迟时间最短，变刚度弹簧F3N次之，F2N所用时间最长；但变刚度弹簧F3N关闭时液压缸下腔的保持压力最高，压力控制精度最高。

由此可见，采用变刚度弹簧能降低大流量安全阀的超调量，使安全阀在冲击载荷下快速稳定，减小阀芯的震荡，并且提高安全阀的压力控制精度，改善安全阀的动态特性。

由于机械式弹簧在1 000 L/min直动式安全阀中结构和空间上的局限性，在AMESim仿真模型中，将普通机械式弹簧改型为以氮气为气体弹簧[13]的新型安全阀(如图15所示)，其结构如图16所示。设定合适的气体压力和作用面积后，得到如图17所示的仿真结果曲线。

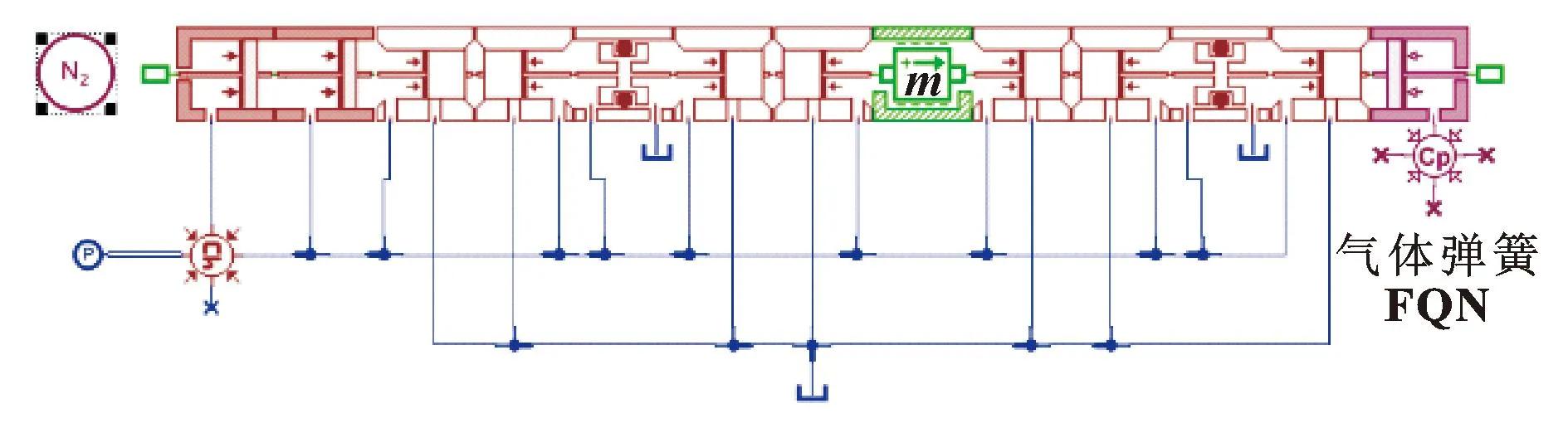
图15 以氮气为弹簧的安全阀仿真模型Fig.15 Simulation model of safety valve with nitrogen as spring

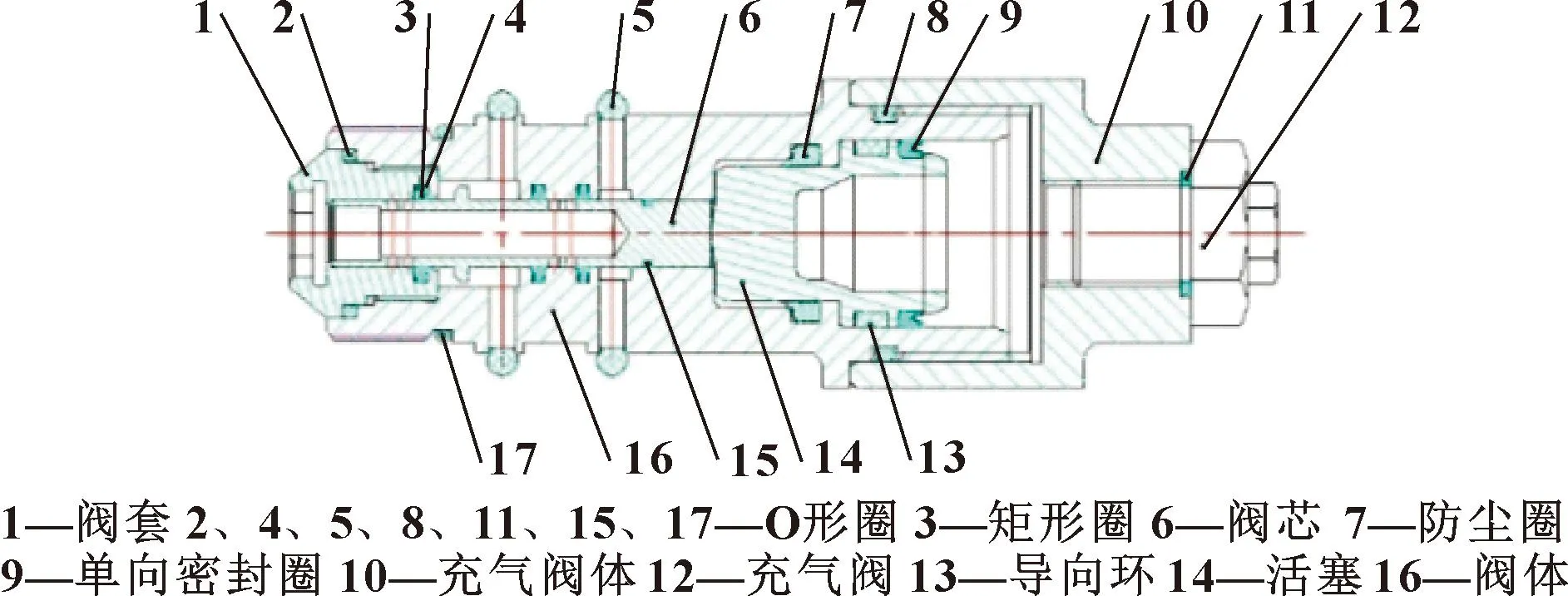
图16 氮气弹簧安全阀结构Fig.16 Structure of nitrogen spring safety valve

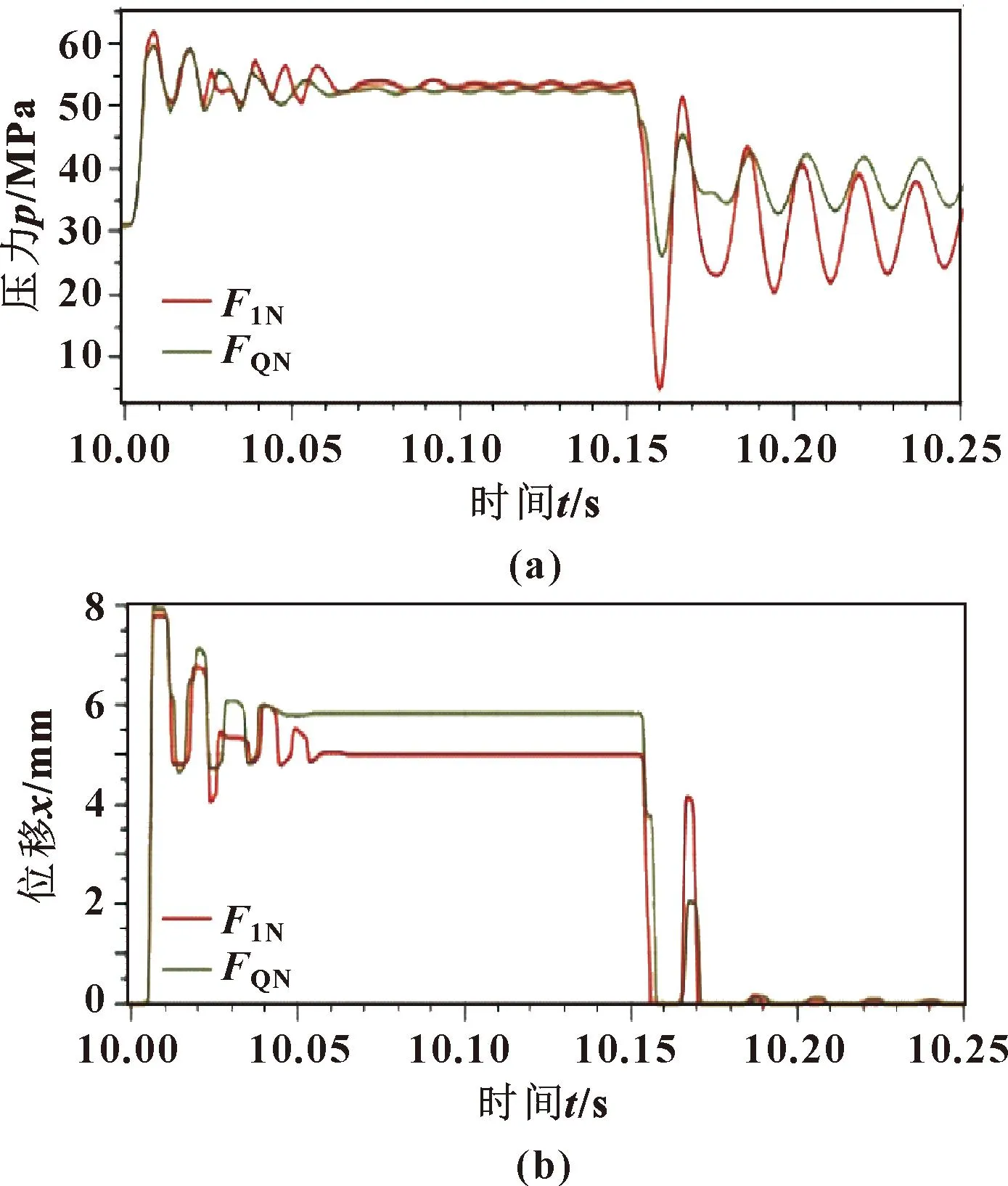
图17 氮气弹簧压力(a)和阀芯位移(b)曲线Fig.17 Pressure(a)and spool displacement(b)curves of nitrogen spring

由图17可知，使用以氮气为气体弹簧FQN的新结构安全阀在相同加载试验条件下，峰值压力为59.5 MPa，超调量为9.5 MPa，压力稳定时间为61.4 ms，开启延迟时间保持不变，均为4.5 ms。安全阀结束溢流时间段内，当安全阀阀芯位移恢复为0时，使用气体弹簧安全阀的液压缸内压力为35.61 MPa，关闭时间为10.157 s，关闭延迟时间为78 ms。与弹簧刚度为334.8 N/mm的定刚度弹簧相比，使用氮气弹簧的安全阀关闭延迟时间和控制精度相当，压力超调量更小，且氮气弹簧结构更易于实现，因此氮气弹簧安全阀的性能更好。

4 结论

(1)文中针对典型的1 000 L/min直动式安全阀进行了数学建模和AMESim仿真分析，数学模型和仿真模型相互印证，验证了仿真模型的正确性，并针对弹簧刚度这一变量，分析定刚度弹簧和变刚度弹簧2种不同类型弹簧下大流量安全阀的响应特性，得到了包括压力、流量和阀芯位移在内的响应曲线。

(2)分析不同弹簧刚度时安全阀的响应曲线可知，当定刚度弹簧刚度由334.8 N/mm减小至285 N/mm时，安全阀超调量由11.7 MPa 减小到9.5 MPa，但阀芯震荡严重，液压缸下腔压力波动较大，不能趋于稳定；刚度由334.8 N/mm增加至385 N/mm时，安全阀超调量增大到14.8 MPa，不利于立柱下腔压力的及时卸载，危害煤矿工人的安全。变刚度弹簧F2N和F3N均能有效降低安全阀的超调量，F2N最为明显，使超调量降低为6.8 MPa，压力稳定时间也由75.3 ms 减小至54.3 ms，同时F3N在关闭时液压缸下腔的保持压力最高，压力控制精度最高。

(3)氮气气体弹簧的仿真结果表明：氮气弹簧作为结构上易于实现的变刚度弹簧，开启延迟时间保持不变，超调量降低为9.5 MPa，压力稳定时间为61.4 ms，比1 000 L/min直动式安全阀超调量更小，卸荷更快。

(4)在理论研究方面，可以为高压大流量安全阀在弹簧方面的优化提供新思路，也为以氮气为弹簧的新型安全阀的冲击载荷实验提供了理论基础。