机载LiDAR姿态角稳定装置的神经网络逆系统解耦控制研究

李旭辉, 李旭东, 王建军, 程霄霄, 聂栋栋, 王光彬

(1.山东理工大学机械工程学院,山东 淄博 255000; 2.山东信质检测有限公司,山东 淄博 255000;3.山东天骏清洁设备有限公司,山东 淄博 255000)

0 引言

机载激光雷达(LiDAR)作为一种新型三维成像技术,在地形测绘、城市建模、文物修复、资源勘探等方面正得到日益广泛的重视和应用[1-2]。机载LiDAR在对地扫描过程中,由于飞机易受湍流、侧风、发动机振动等多方面的因素干扰,机载平台的姿态角会有显著波动,从而会影响激光点云的密度分布,并最终影响由激光点云重建的三维数字模型的成像精度[3-4]。因此,文献[5]设计了一种可有效减小机载设备体积的紧凑型姿态角稳定装置,能通过推转方式实时补偿机载平台的三轴姿态角的波动对LiDAR扫描点云的恶劣影响。设计的紧凑型姿态角稳定装置,其本质上是一个复杂的多输入多输出、非线性和强耦合系统,因此,为了实现高精度控制和提高抗干扰能力,有必要对控制系统进行有效的解耦处理[6-8]。

通常的解耦控制方法主要有传统的解耦控制方法、自适应的解耦控制方法和智能的解耦控制方法3大类[9]。传统解耦控制主要包括前置补偿法和现代频率法,主要适合于线性定常控制系统的解耦。逆系统解耦是传统解耦方式中的一种,其基本思想为:当原系统可逆并能构造出逆系统,将逆系统串接在原系统之前,则构成的伪线性复合系统的各输入输出之间为线性传递函数关系。崔晶等[10]采用逆系统前馈方法对x-y精密定位平台进行了误差补偿。但实际工程应用中,非线性系统难以建立精确解析式,即使建立起精确的非线性数学模型,求解其逆系统时往往也非常困难[11]。自适应解耦控制方法是将自适应控制技术与解耦控制相结合,主要适用于参数未知及时变系统的解耦控制,其可解决非线性、强耦合系统的实时动态解耦控制,但要求在线辨识控制系统的模型,故计算量大,对各种扰动的适应能力差[12]。智能解耦控制方法是近年来最新的解耦控制方法,主要有神经网络解耦控制和模糊解耦控制等,其对解决非线性耦合系统有显著优势[13]。

目前人工神经网络得到了较广泛的应用,其具有多输入、多输出特点,是一种优秀的非线性函数逼近方法,其中,BP神经网络采用误差反向传播算法,当隐含层和节点数选择适当时,可逼近任意非线性映射关系[14-15]。因此,可将逆系统解耦思想与可实现非线性函数逼近的BP人工神经网络结合,突破逆系统解耦方法中需建立精确数学模型的弊端,成为复杂非线性系统解耦的新方法[10,16]。

国内外对神经网络逆系统解耦进行了大量研究[17-21]。比如,夏光等[17]采用神经网络逆系统进行了叉车主动后轮转向与横摆力矩的控制解耦;刘国海等[18]提出了一种基于神经网络逆系统实现了对发酵复杂过程的解耦控制;刘根水等[19]针对机械手系统具有非线性时变、多变量和强耦合的特点,采用了基于RBF神经网络逆系统实现了机械手的解耦控制;MENG等[20]采用伪线性神经网络逆系统解耦方法,实现了集热器的压力解耦控制;SUN等[21]提出了模糊神经网络逆系统的解耦控制方法,可将非线性多变量系统解耦成相互独立的单输入单输出伪线性子系统;另外,文献[22-23]通过学习迭代获得了三轴转台的神经网络逆系统模型,将其作为前向控制器与三轴转台控制系统串联形成伪线性系统,实现了三轴转台的解耦控制;FANG等[24]获得了三轴转台的神经网络逆系统建模,将其作为反馈补偿器,进行了控制系统的解耦,并大大提高了系统的抗干扰性。

综上,为了克服设计的机载LiDAR姿态角稳定装置控制系统的复杂非线性耦合缺点,本文首先分析了设计的姿态角稳定装置的动力学模型,其次提出了神经网络逆系统解耦的实现方法,最后进行了仿真实验,证明提出的神经网络逆系统解耦系统可有效降低控制耦合,并有效提高控制系统的精度及控制系统的抗干扰性和动态性能。

1 神经网络逆系统解耦总体方法

机载LiDAR姿态角稳定装置的机械结构[5]见图1。

图1 机载LiDAR姿态角稳定装置的机械结构

图1中,为了使出射激光的指向不受机载平台的姿态角振动的影响而能始终保持稳定,采用推扫式大尺寸激光反射镜对出射激光的指向进行补偿。其中,大尺寸激光反射镜通过x轴和y轴的两个直动电机,通过直线运动实现转动运动,使激光反射镜绕x轴和y轴的自由转动,以稳定出射激光束的空间指向。另外,z轴采用立式转轴,下端安装在立式滚动轴承中进行转动控制。其工作原理为:当机载平台的姿态角波动时,采用直动电机驱动激光扫描镜绕x轴和y轴反向转动滚动角和俯仰角的一半,并采用转动电机驱动齿轮机构绕z轴反向转动偏航角的角度,从而可实现对机载平台滚动角、俯仰角和偏航角的分别补偿,使机载LiDAR工作时免受机载平台姿态角变化的影响。但这个装置在控制过程中,三轴的转动控制存在严重的耦合性,导致控制精度不高,需要进行解耦控制。因此,设计了神经网络逆系统解耦方法,其总体方法如图2所示。

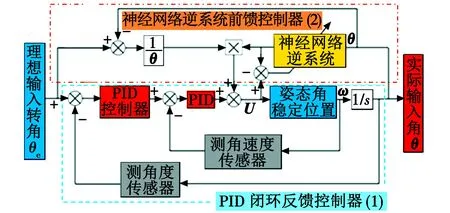
图2 机载LiDAR姿态角稳定装置控制系统解耦总体方法

根据神经网络逆系统解耦思想,对于设计的机载LiDAR姿态角稳定装置控制系统,获得其非线性控制系统的逆系统,采用静态神经网络和若干积分器共同组成动态神经网络来构造其逆系统,将逆系统与控制系统串联可实现解耦处理获得线性化控制系统,继而对解耦后的各子系统设计反馈控制器,从而可改善控制系统的静特性、动特性和抗干扰能力。图2中,共有两大主要控制器,即PID闭环反馈控制器(1)和神经网络逆系统前馈控制器(2),两者构成了“PID反馈+神经网络逆系统前馈的复合解耦控制器”。其中,在神经网络逆系统前馈控制器(2)中,当理想输入转角θe经过PID反馈控制器的调整后,响应输出量作为姿态角稳定装置中的控制电机的输入控制电压,即U=[Ux,Uy,Uz]T。而姿态角稳定装置的响应输出信号为三轴转动的角速度ω矢量,其通过积分作用即为三轴的实际输入转角,即θ矢量。继而,θ矢量经测角传感器测量后,其信号分为两路进行反馈控制:一路是与理想的输入转角进行比较,求出差值,再乘以比例系数1/θ进行调节,从而得到输出角度误差值的相对比值;另一路经神经网络逆系统后,获得与输入角度θ相对应的控制电压值修正值,将输出角度误差的相对比值与经过神经网络逆系统的输出控制电压修正值相乘,可用于修正姿态角稳定装置三轴控制电机的输入控制电压U,从而达到解耦控制的目的。

2 姿态角稳定装置的正、逆控制系统建模

2.1 正向控制系统的建模

姿态角稳定装置设计的独特之处在于,扫描镜绕x轴和y轴的转动是绕中心处的万向球面轴承,与传统的框架式三轴转台相比,相当于三轴转台的中框和内框合并在一起,故中框可视为不存在。设Jxi,Jyi,Jzi和ωxi,ωyi,ωzi分别为内环(激光扫描镜)绕x,y,z轴的转动惯量和角速度;Jxo,Jyo,Jzo和ωxo,ωyo,ωzo分别为外环(激光扫描镜+立式转轴机构)绕x,y,z轴的转动惯量和角速度;α,β,γ分别为绕x,y,z轴的转角。由刚体动能公式,可得到姿态角稳定装置的总动能T为

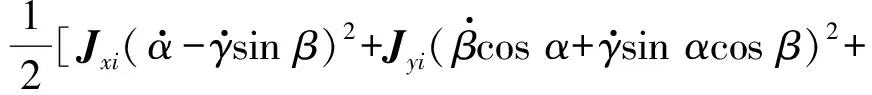
(1)

设M=[Mx,My,Mz],为作用在x,y,z轴上的转动力矩矢量。由力学拉格朗日方程可得姿态角稳定装置的动力学方程为

(2)

选用直流力矩电机驱动,由电机控制理论可知,直流力矩电机控制电压与电机输出力矩成正比,即

M(x,y,z)=Kt/Ra·U(x,y,z)=K(x,y,z)·U(x,y,z)

(3)

式中:M(x,y,z)为绕x,y,z轴的电机输出力矩矩阵;K(x,y,z)为绕x,y,z轴驱动电压与输出力矩的关系系数矩阵;U(x,y,z)为分别绕x,y,z轴的直流力矩电机控制电压矩阵;Kt为电机力矩系数;Ra为电机内阻。姿态角稳定装置中驱动x轴与y轴采用208系列8-2105力矩电机,其Kt=1.19 N·m/A,Ra=5.1 Ω;z轴采用288系列11-2105电机,其Kt=6.23 N·m/A,Ra=9.1 Ω。

由式(3)可得Kx=Ky=0.233,Kz=0.685,Kx,Ky,Kz分别为绕x,y,z轴驱动电压与输出力矩的关系系数。由姿态角稳定装置的机械结构,三轴转动惯量为Jxo=Jyo=0.004 kg·m2,Jzo=0.002 kg·m2,Jxi=Jyi=0.003 kg·m2,Jzi=0.001 kg·m2。

将式(3)代入式(2),得三轴的控制电压与输出角运动量之间的动力学方程为

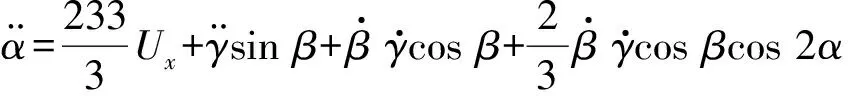
(4)

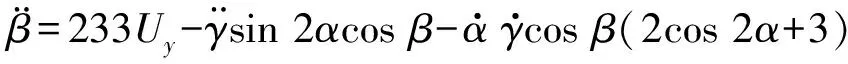
(5)

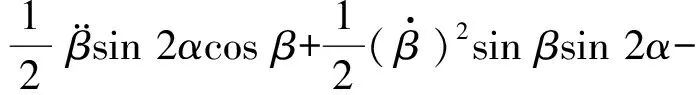
(6)

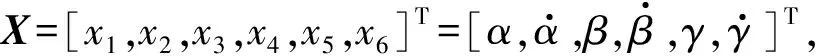
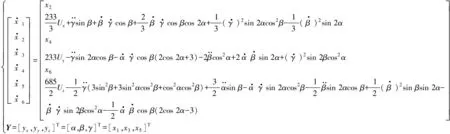
(7)

由式(7)可见,姿态角稳定装置动力学系统是一个三输入、三输出的复杂非线性系统,存在耦合关系,因此需要对三轴转动控制进行解耦处理。

2.2 控制系统的可逆性分析

由式(7)描述的多输入多输出系统,可采用Interactor算法证明其可逆性[7]:计算输出变量Y对时间的各阶导数,直到输出的导数方程中显含输入变量控制电压U=[Ux,Uy,Uz]。由式(7)得

(8)

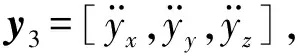
(9)

由于存在非负数α1,α2,α3使得t3等于系统输出变量数,由隐函数定理可知,式(7)的逆系统存在[8]。

2.3 基于神经网络的逆控制系统建模

本文构造的神经网络逆系统结构如图3所示。

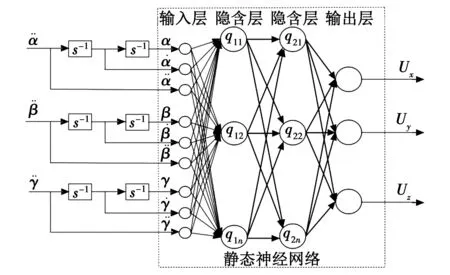
图3 姿态角稳定装置的神经网络逆系统建模

3 基于神经网络逆系统的解耦控制仿真实验

基于式(7)的姿态角稳定装置动力学模型及图3的神经网络逆系统模型,对图2进行控制系统仿真。为验证基于神经网络逆系统解耦方法的有效性,将采用单纯PID闭环反馈控制器(1)的控制效果与采用PID反馈控制器(1)+神经网络逆系统前馈控制器(2)相结合的复合控制解耦方法的控制效果进行了对比分析。

3.1 单纯PID闭环反馈控制器的控制性能仿真实验

在图2中,只保留经典PID闭环反馈控制器(1),对控制系统进行仿真。αe,βe,γe为三轴姿态角稳定装置分别绕x,y,z轴的理想输入角,Ux,Uy,Uz为三轴驱动电机的输入控制电压信号,αr,βr,γr为三轴的实际输出角。经仿真分析,3个轴的PID控制器的控制参数分别为Px=2,Ix=2,Dx=0.5,Py=2,Iy=2,Dy=0.5,Pz=2,Iz=1,Dz=0.4。当3个理想输入角αe,βe,γe分别取幅值1°,2°,3°,周期为2π的正弦信号时,输出响应误差曲线(即Δα=αr-αe,Δβ=βr-βe,Δγ=γr-γe),如图4(a)所示。

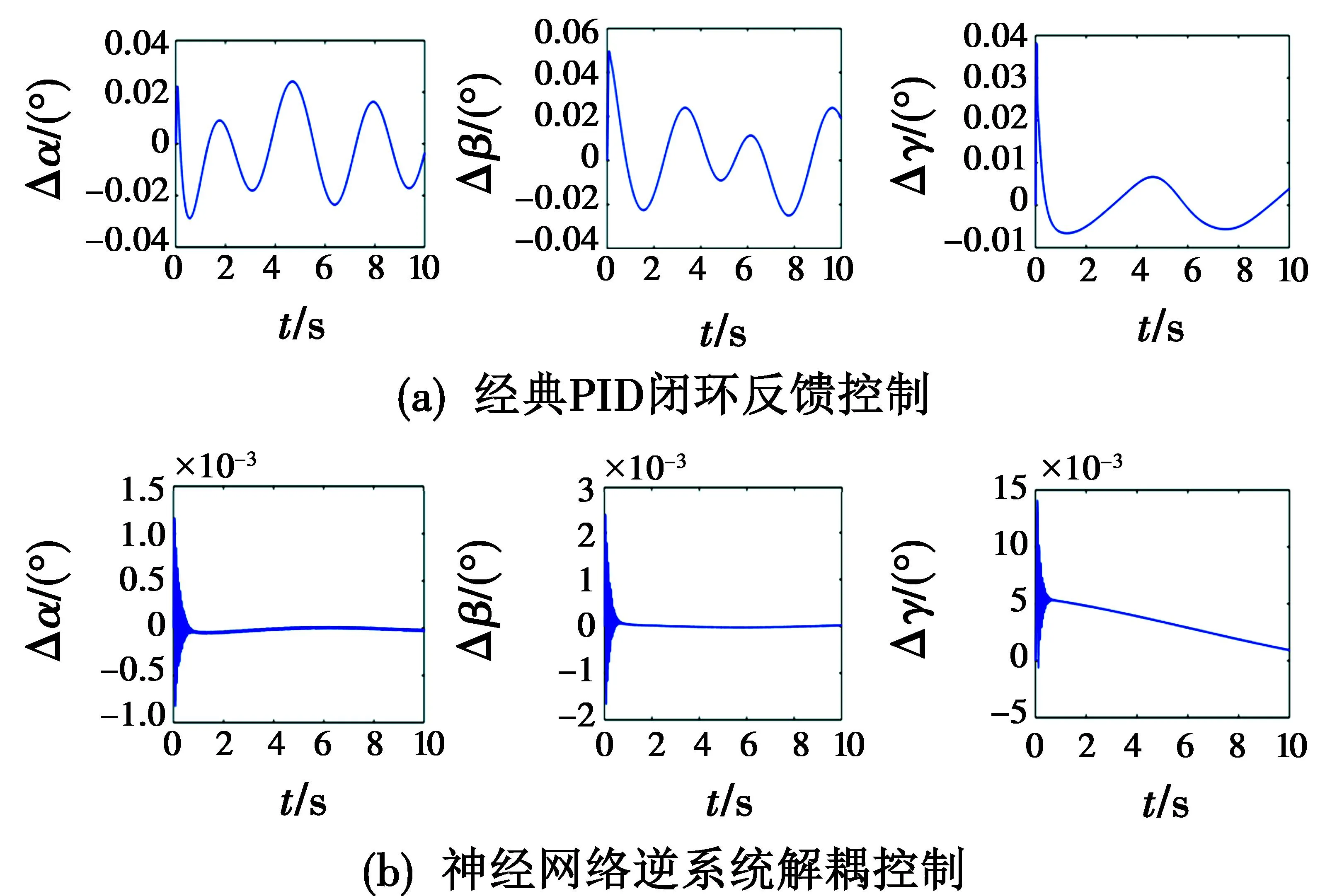
图4 两种控制方法下的系统输出响应误差曲线

由图4可见,采用单纯PID闭环反馈控制对给定输入轨迹基本上能实现有效跟踪,但控制系统存在较大误差,主要源于单纯闭环反馈难以实现解耦控制并获得较高的控制精度。另外,当三轴姿态角稳定装置的工况发生变化时,控制系统的误差会变大,耦合会增强,对控制精度影响显著。

3.2 基于PID反馈控制器(1)+神经网络逆系统前馈控制器(2)的复合控制仿真实验

按图2所示,采用神经网络逆系统前馈控制器+ PID闭环反馈器的复合解耦控制器,3个轴的PID控制器的控制参数与3.1节的实验参数相同,没有改变,进行仿真。当3个理想输入角αe,βe,γe分别取幅值1°,2°,3°、周期为2π的正弦信号时,输出响应误差曲线(即Δα,Δβ,Δγ)如图4(b)所示。

与图4(a)相比可见,在增加神经网络逆系统解耦控制后,控制系统的输出响应误差显著减小,三轴姿态角稳定装置控制系统的耦合效应得到了良好抑制。

3.3 两种控制方法的控制误差对比

表1为图4正弦输入时无随机测量误差干扰时的输出角误差的RMSE值。

表1 两种控制方法下的输出响应误差的RMSE值比较

通过表1对比可见,采用了神经网络逆系统解耦控制的效果要明显优于单纯采用经典PID闭环反馈控制的效果,尤其是对x轴和y轴的输出响应误差更小。

3.4 两种控制方法的抗干扰性能分析

为分析两种控制方法下,控制系统对随机误差干扰的鲁棒性,将测角度反馈传感器的随机测量误差信号作为干扰信号施加在控制系统中,均值为-0.004°、标准差为0.326°的高斯随机分布噪声。分析在此误差干扰下,两种控制方法的输出性能。经典PID闭环反馈控制方法控制系统的输出响应误差曲线如图5(a)所示,基于神经网络逆系统解耦控制的输出响应误差曲线如图5(b)所示。

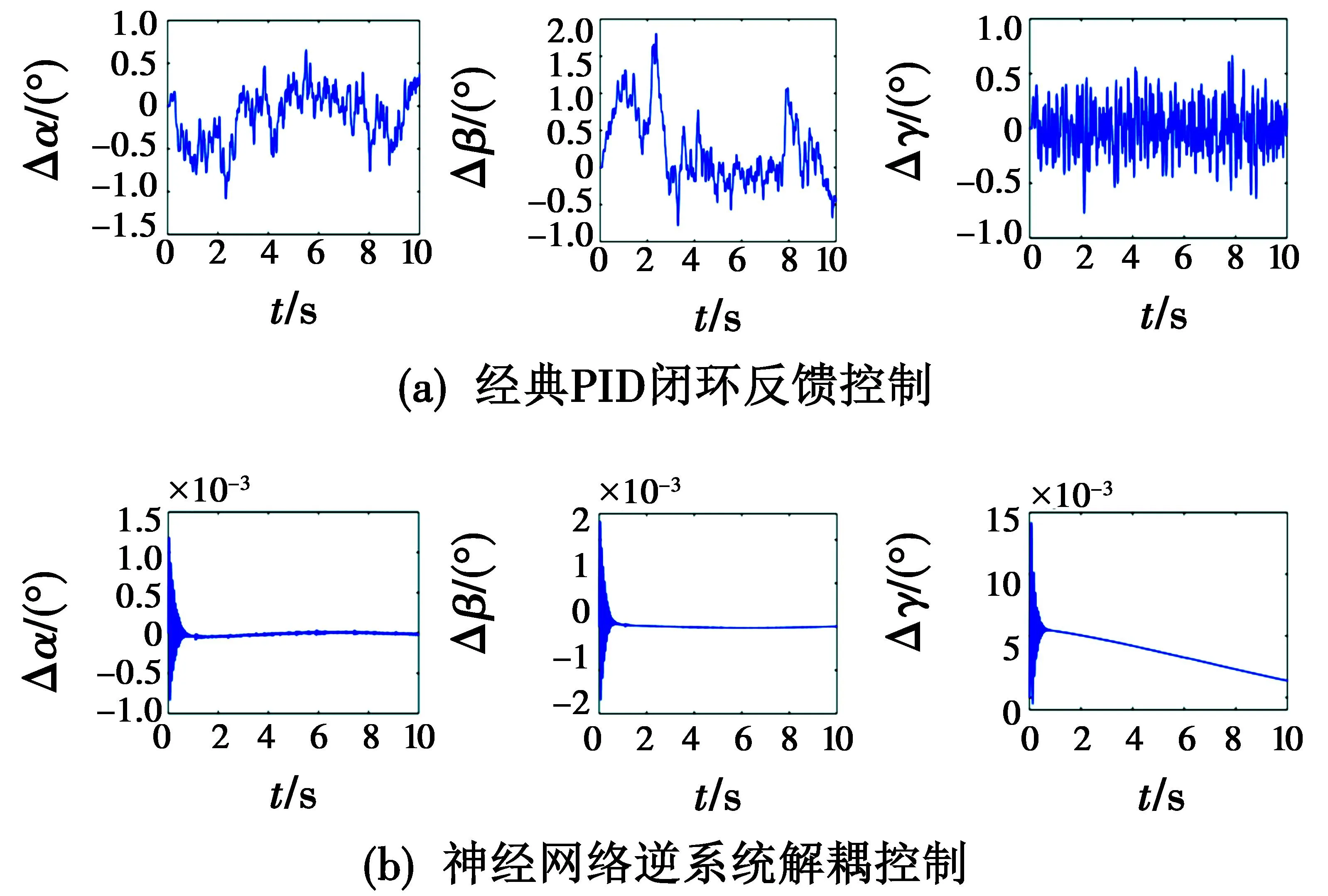
图5 两种控制方法对随机误差干扰的鲁棒性分析

从表1的实验结果看,单独采用PID控制,与复合控制的控制效果对比,在x轴和y轴的精度提高明显,可看出解耦效果明显;而z轴的控制精度虽有所提高,但改善效果不是很显著,其本质原因还在于z轴控制相对独立,与x轴和y轴耦合不太显著。

z轴的误差在10 s内存在单一方向偏差,但控制误差不会造成累积。因为每个控制周期都会以z轴的转动传感器进行转角定位,每个控制周期结束虽有控制误差,但控制误差在后续控制周期中不会累积。收敛速度较慢,但其误差实际上已经可满足大多数控制精度的要求,如果想进一步满足更高的实际应用控制精度,可从PID反馈控制上进一步改善,如控制参数优化等措施。

表2为正弦输入时有随机测量误差干扰时,在两种控制方法下的控制系统输出响应误差的RMSE值。

表2 随机测量误差干扰下两种控制方法的响应误差RMSE值比较

由表2结果可知,本文所提出的神经网络逆系统解耦控制比经典PID闭环反馈控制对抵抗随机误差干扰的鲁棒性更好,大大减小了输出响应误差。可见,在外界干扰作用下,采用神经网络逆系统解耦控制的系统稳定性更好,具有更优良的抗干扰鲁棒性。

4 结论

为补偿机载平台姿态角波动对机载LiDAR测量点云的不利影响,设计了一种推扫式大尺寸激光反射镜的三轴姿态角稳定装置。由于设计的姿态角稳定装置具有非线性、强耦合特性,因此,为提高控制系统的精度和动态性能,本文对控制系统进行解耦方法设计和仿真实验验证。首先,建立设计的姿态角稳定装置的控制系统模型,分析三轴转角的控制耦合特性;其次,分析姿态角稳定装置控制系统的可逆性,基于神经网络,训练获得姿态角稳定装置控制系统的逆系统模型;然后,将PID反馈控制器与神经网络逆系统前馈补偿器组成前馈-反馈复合控制器,实现了姿态角稳定装置控制系统的实时解耦。最后进行了仿真实验,结果表明:采用单纯PID反馈控制器,三轴输出转角误差均方根值分别为0.0146°,0.0169°和0.0054°;采用复合神经网络逆系统解耦控制,三轴输出转角误差均方根值分别为9.5773E-5 (°),1.8704E-4 (°)和0.0037°。从而证明所设计的神经网络逆系统解耦控制方法具有优良的控制性能。另外,分析神经网络逆系统解耦控制对随机测量误差干扰的优化能力,表明解耦控制系统具有优良的抗干扰性。