基于Hoek-Brown的双向不等压隧道支护估算及工程应用

2024-01-12李守宇宋浩然李靖铭支永辉李涛张庆文

科学技术与工程 2023年34期

李守宇, 宋浩然, 李靖铭, 支永辉, 李涛, 张庆文*

(1.西南林业大学土木工程学院, 昆明 650224; 2.中铁开发投资集团有限公司, 昆明 650200;3.中铁一局集团第五工程有限公司, 宝鸡 721006)

在地下结构稳定性研究中,岩体的层理面、围岩材料的强度参数、初始地应力都决定着地下结构稳定性,同时也决定着施工工艺和支护参数。Mohr-Coulomb强度准则(以下简称M-C强度准则)在岩石研究中是最简便的,但其并不能真实反映岩石高围压下的破坏情况。Hoek等[1-2]提出Hoek-Brown强度统一强度准则(以下简称H-B强度准则),因其适用于岩石从拉伸-低围压-高围压全过程的破坏,所以在地下工程领域中被广泛地应用。

王洪涛等[3]基于非线性H-B强度准则构造了锚索悬吊条件下的顶煤曲线破坏力学模型,研究表明上层覆土及岩体扰动系数D(经验参数)与所需锚固力成正比。郑艳妮等[4]通过微结构张量法,分析岩样层理面对岩石最终破坏类型的影响,并结合大量页岩的单轴压缩试验,提出更切合页岩破坏曲线的修正H-B强度准则。苏雅等[5]基于H-B强度准则,建立了针对软岩隧道极限变形的估算方法,并结合Rabcewicz等[6-7]提出的滑移剪切模型,分析了国际地质指标(geological strength index,GSI)与隧道开挖半径、位移之间的相关敏感度。王志龙等[8]基于H-B强度准则和winker地基对静水压力状态下的圆形隧道支护结构进行求解,并以向家湾隧道项目为实际依托进行支护结构估算,估算结果符合规范取值范围。石欣等[9]通过多椎体块破坏机制极限分析,建立了非线性H-B破坏准则对隧道开挖面稳定性进行研究,将修正模型代入隧道的掌子面稳定性中进行分析,结果表明H-B修正公式准确率明显高于M-C强度准则,同时开挖面极限支护力影响规律与围岩规律遵循M-C强度准则。潘阳等[10]在计算圆形隧道塑性区时,将H-B估算结果与M-C结果进行对比,发现M-C估算结果过于保守,不能精准的预估隧道的塑性状态。

上述学者基于广义H-B强度准则建立力学模型进行分析[11-14],但在推理过程中均未考虑初始地应力,默认围岩处于静水压力状态下,即侧压系数λ= 1,忽略侧压力带来的影响。现参考上述学者对H-B强度准则的研究,结合双向不等压隧道的研究分析[15-18],提出H-B强度准则在双向不等压隧道围岩塑性区计算式,以侧压力、支护参数作为自变量,在不同角度θ下,对圆形隧道的塑性区半径和应力进行分析,并依托滇中引水工程板凳山隧洞,对具有微膨胀性的粉砂质泥岩进行塑性分析,结合滑移剪切模型对极限位移量以及最小支护应力进行极限估算。

1 围岩塑性区及极限支护

1.1 基本假定

研究分析了非静水压力状态下圆形隧道的塑性半径及应力状态,结合滑移剪切模型进行支护估算。为简化计算模型,做出以下假定:①围岩为均质体、各向同性的连续介质;②隧道形状为规则的圆形;③隧道为深埋隧道,可将其简化为无限体中的孔洞问题;④假定隧道长度无限长,并沿隧道纵向取1 m长度作为研究对象;⑤忽略由于爆破等因素产生的围岩松弛;⑥将非静水压力带来的荷载简化为双向不等压模型进行分析;⑦隧道内部存在着支护应力pi(pi≥0),当无支护式可视为pi=0。

1.2 理论推导

1.2.1 弹性区应力

将非静水压力状态下隧道受力状态简化为如图1(a)所示,力学模型左右两侧受均布压力σx、上下两端受均布压力σz,并满足σx=λσz。可将其拆解为轴对称模型和非轴对称模型,对其进行叠加分析,即如图1(b)和图1(c)叠加处理。

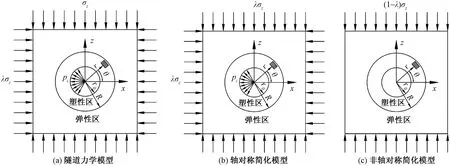
R为隧道塑性半径;r0为隧道开挖半径;r为计算处半径;λ为围岩的侧压力系数,取值范围为λ=0～1;θ为计算岩体与隧道开挖水平方向右侧的夹角图1 应力分析简化模型Fig.1 Simplified model for stress analysis

在轴对称模型中,假定围岩边界无限大,可视为厚壁圆筒受均布荷载,应力情况可采用拉梅解答。

(1)

式(1)中:σre1为弹性区径向应力;σθe1为弹性区环向应力;λ为侧压力系数;σz为隧洞竖直方向所受应力;σR为塑性边界上的径向应力;在弹性计算中r取值范围为r≥R。

非轴对称模型可视为上下受均布荷载的薄壁中心孔洞的柯西问题,应用弹性力学应力平衡方程,并考虑其边界条件对其进行分析,可得到

(2)

式(2)中:σre2为弹性区径向应力;σθe2为弹性区环向应力;τrθ为弹性区的切向应力;θ取值范围-90°≤θ≤90°。

将拉梅解答和柯西问题的解答进行叠加,则可得到总应力为

(3)

1.2.2 塑性区应力

在非轴对称荷载作用下,应力平衡方程为

(4)

分析隧道塑性区应力状况可知,σθp为最大主应力,σrp为最小主应力,将H-B强度准则改写为

(5)

式(5)中:σθp、σrp分别为岩体材料破坏的最大、最小主应力,MPa;σc为岩体单轴抗压强度,MPa;mb、s、α为与岩体材料特征相关的经验参数,无量纲。

联立式(4)和式(5),并考虑边界条件r=r0时σrp=pi,τrθ=0可解出径向应力和环向应力的表达式为

(6)

式(6)中:在塑性计算中r取值r0≤r≤R。

1.2.3 塑性半径

在弹塑性边界r=R处存在σre=σrp=σR,σθe=σθp,联立式(3)和式(6)可得

(7)

式(7)表明径向应力σrp与角度无关,仅与围岩材料和支护应力相关;而环向应力σθp不仅与围岩材料和支护应力相关,同时还受侧压力系数和角度的影响。根据式(7)对塑性半径R进行进一步计算。

(8)

式(8)中:

(9)

(10)

在确定经验参数mb、α、s后,分析式(8)可知:塑性半径与单轴抗压强度、支护应力成反比;塑性半径与围岩压力、计算角度的cos2θ成正比,当1-2cos2θ>0,R与λ成正比,即-30°<θ<30°时R随λ的增大而增大;当1-2cos2θ<0时,R与λ成反比,即θ<-30°及θ>30°时R随λ的增大而减小。在确定经验参数及围岩材料参数后,R随λ的增大呈现上下端部小、中间部分大的椭圆形,如图2所示。

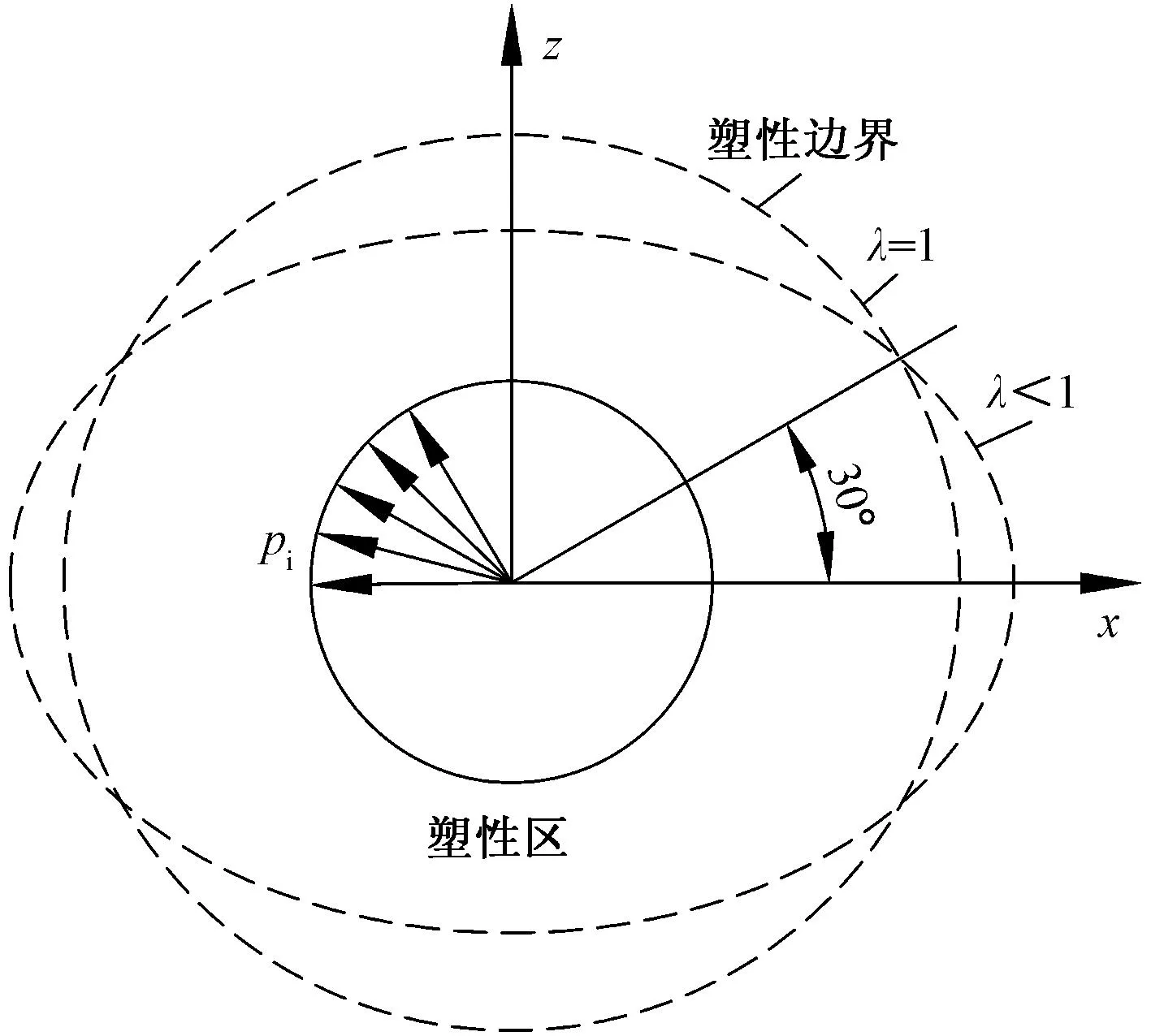
图2 塑性边界示意图Fig.2 Schematic diagram of plastic boundary

1.2.4 最小支护应力

新奥法提出者Rabcewicz[6-7]于1964年提出了剪切滑移破坏理论,认为在软弱地下结构开挖后,在荷载(λ≤1)作用下,围岩因受剪而产生松弛,于隧道两侧形成压力集中而产生滑移剪切面,随压力不断增加,B值增大。围岩节理裂隙扩展导致的破坏可看作为楔形滑移体,即剪切滑移破坏模式,如图3所示。

b为剪切体的宽度图3 滑移剪切模型Fig.3 The sliding shear model

结合式(8)计算的最大塑性半径,结合剪切滑移模型,最小支护应力pi,min可以进行近似估算,即

(11)

式(11)中:R0,max为式(8)中所计算的最大塑性半径;γ为围岩重度,kN/m3。

1.2.5 最大允许位移量

在对围岩位移量进行研究时,假设某隧道开挖半径r0,未受扰动围岩泊松比μ,剪切模量G,隧道受静水压力σz。Carranza-Torres等[19-20]提出了隧道允许最大变形量umax为

(12)

(13)

(14)

将式(8)中最大塑性半径以及式(11)中最小支护应力代入式(12)即可求解出最大允许位移量。

2 工程计算

2.1 工程概况及参数选取

选取滇中引水工程板凳山隧洞作为实际工程依托,对本文所推导公式进行验算。板凳山隧洞全长11.153 km,最大埋深372 m,净空断面尺寸8.96 m。围岩以粉砂质泥岩为主,围岩等级为Ⅴ级。选取板凳山隧洞上游断面(DK95+910)和下游断面(DK98+250)作为试验监测断面。

隧洞断面为马蹄形,如图4所示。本文研究以当量半径法[21-22]为理论指导,根据式(15)将马蹄形隧道简化为圆形隧道,计算后取r0=6.0 m。

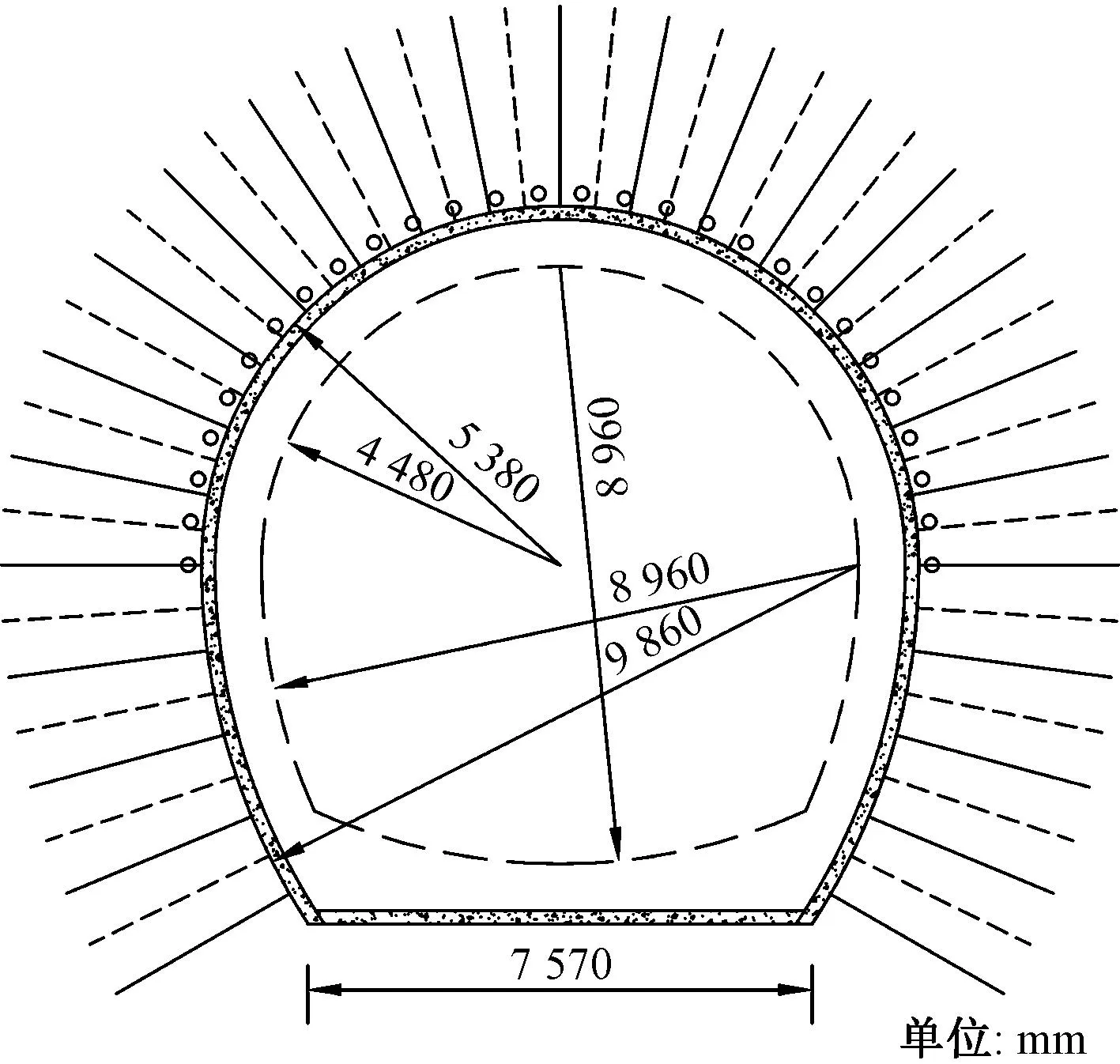
图4 隧洞断面Fig.4 Tunnel cross section

图5 围岩断面图Fig.5 Surrending rock section

(15)

式(15)中:r0为隧洞当量半径取值,m;S为实际隧洞截面面积,m2,板凳山隧洞截面面积为96.474 m2;k为断面形状修正系数,马蹄形截面取k=1.075。

通过地质勘探报告、现场试验和室内实验,对围岩参数进行取值。使用直径为50 mm、高度为100 mm的标准岩样进行室内实验,实验前使用砂纸进行精细打磨将表面误差控制在0.01 mm以内,如图6所示。在中国的工程地质评估中常采用BQ法进行评估,宋彦辉等[23]以黄河上游玛尔挡水电站坝基岩体为试样,通过大量剪切实验并参考规范建议值,建立BQ与GSI的相关关系,即

图6 岩石试验Fig.6 Rocks test sample

GSI=1.418 5BQ0.624 1-5

(16)

式(16)中:GSI为国际地质指标;BQ为中国常用的衡量指标,包含岩石单轴饱和抗压强度σRc和岩体的完整性系数Kv。

在以上述参数为基础进行计算,整理后数据如表1所示。

表1 围岩材料参数Table 1 Surrounding rock material parameters

2.2 计算分析

综合式(1)～式(16),以表1中围岩材料参数为基础,采用单一变量法分析侧压力系数λ、支护应力pi两个自变量在不同角度θ下对塑性半径R、轴向应力σr、环向应力σθ的敏感度影响。

2.2.1 围岩侧压力影响

通过对式(7)分析可知,轴向应力σr仅与围岩材料和支护应力相关,不受侧压力的影响;而环向应力σθ不仅与围岩材料和支护应力相关,同时还受侧压力系数和角度的影响。

为进一步探究侧压力与环向应力的关系,同时增加考虑支护应力的影响,通过式(7)分别对θ在0°和45°进行计算,绘制出在弹塑性边界上λ-pi-σθ三者关系示意图,如图7所示。

图7 应力曲线Fig.7 Stress curve

对比分析图7发现θ在0°的环向应力取值在7～14,而θ在45°的环向应力取值在3.5～10,拱腰处的环向应力明显高于拱肩处。

环向应力与支护应力呈正相,环向应力随支护应力的增加而增加,但支护应力对环向应力的影响为非线性关系。图中表现为支护应力pi≤0.5 MPa时,支护应力与环向应力的关联程度较高,变化曲线较为敏感;支护应力pi>0.5 MPa时,支护应力与环向应力的敏感度降低,变化曲线变化放缓。

侧压力对环向应力的影响为线性关系,但两者的关联在两图中表现不同,在图7(a)中环向应力随着侧压力的增大而降低,呈负相关;而在图7(b)中环向应力随着侧压力的增大而增大,呈正相关。

结合图7进一步分析式(7)发现,θ在0～30°区间,环向应力与侧压力系数成正相关,θ在30°～90°区间,环向应力与侧压力成负相关。在弹塑性边界上,环向应力在θ=30°处取得最大值,形成如图8所示的蝴蝶状曲线。

图8 环向应力变化曲线Fig.8 Tangential stress curve

在隧洞开挖后无支护(pi=0)的情况下,通过式(8)计算出塑性半径,如图9所示。从图9可知,λ=1时塑性区形状为包裹开挖截面的圆形,塑性半径R为19 m;当λ=0时,拱腰出现最大塑性半径R为27.2 m。随着λ的减小,拱顶塑性区范围不断减小,直到λ≤0.38时,拱顶不出现破坏,而拱腰塑性区范围随λ的减小不断扩张。在θ=30°处塑性区范围不受侧压力的影响,与式(8)所表现的规律相吻合。

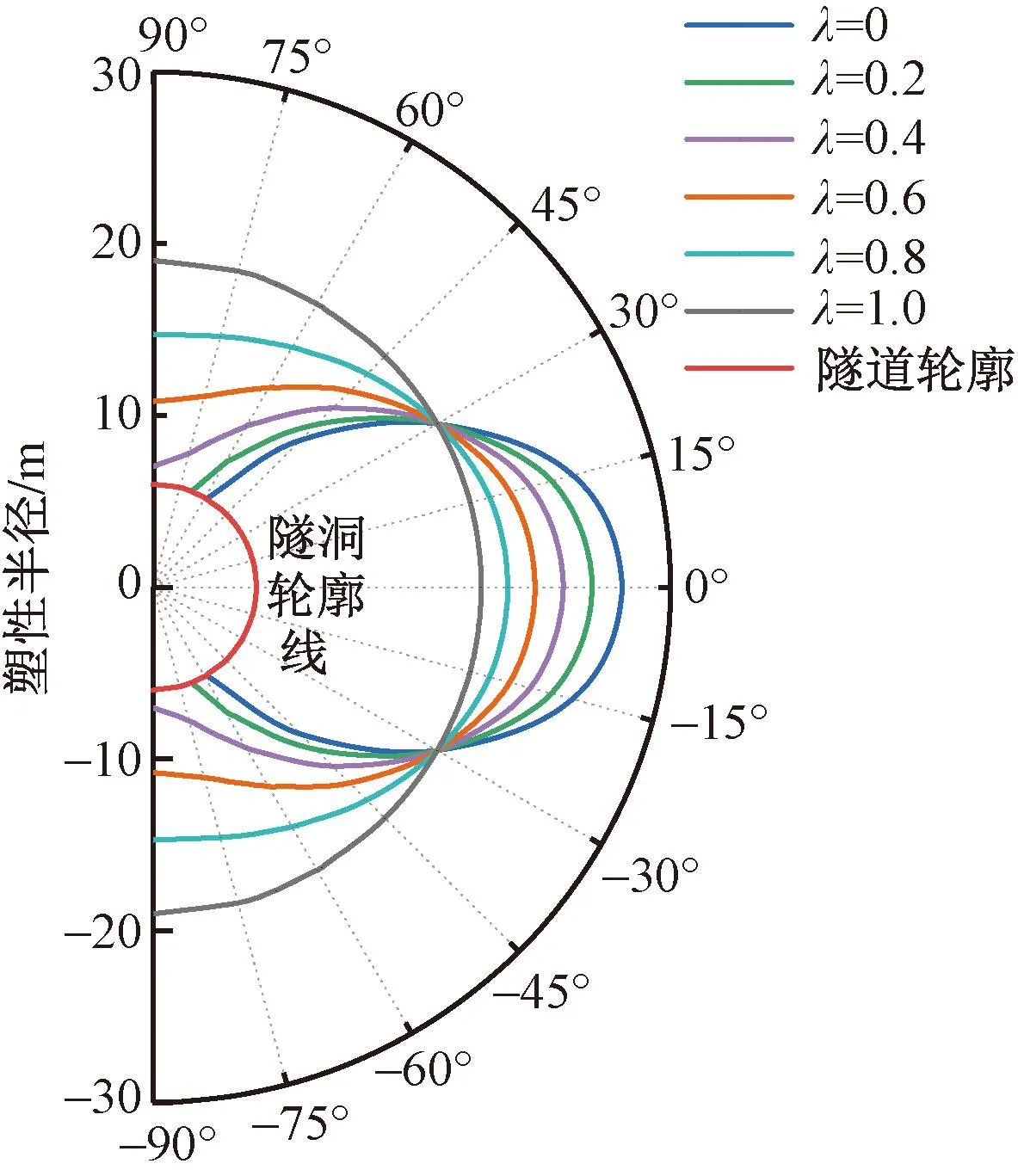
图9 塑性半径-侧压力系数Fig.9 Plastic radius-lateral pressure coefficient

2.2.2 支护应力影响

为探究支护应力与径向应力、环向应力之间的敏感度,将支护应力作为唯一变量,分析径向应力和环向应力的变化。在相同侧压力系数的情况下,根据式(6)计算出随围岩半径增长的切/径向应力值,绘制曲线如图10所示。

图10 应力-半径曲线Fig.10 Stress-radius curve

从径向应力和环向应力分析围岩塑性区发育情况,发现在无支护应力情况下塑性区半径较大,相对较发育,且稳定趋势较为平缓。总体趋势呈现为支护应力越小,应力稳定速率越缓,造成的塑性半径越大。

为研究隧洞支护应力与塑性半径之间的敏感度,选择塑性半径最大位置处(θ=0),根据式(8)计算在各支护应力下所产生的塑性半径,绘制支护应力-塑性半径曲线,结果如图11所示。

图11 塑性半径变化曲线Fig.11 The curve of plastic radius

以塑性半径与开挖半径的比值(R/r0)作为衡量指标,对支护应力与塑性半径之间的敏感度进行分析,以斜率作为衡量稳定趋势的指标(后文中斜率取正值)。在无支护情况下,塑性半径取值范围为19～27.2 m,R/r0=3.17～4.53,斜率K=1.4;当支护强度达到3 MPa时,塑性半径取值范围为8.2～11.8 m,R/r0=1.36～1.96,斜率K=0.2。随着支护应力的增加导致塑性区半径降低,但降低的速率在不断衰减并逐渐趋于平缓。这表明随支护应力的不断增大,支护应力所带来的收益在不断地降低。

以板凳山隧洞为工程依托进行理论分析,使用式(12)计算出隧洞所需最小支护应力pi,min=0.29 MPa,塑性半径为15.2～21.6 m。由分析结果可知,随侧压力系数λ的降低,拱腰处塑性面积不断增加,拱顶塑性面积不断降低,直至λ≤0.38时,拱顶塑性区消失。综合切/径向应力以及围岩塑性半径分析,在满足安全的前提下,板凳山隧洞的最佳支护应力范围在0.5～1 MPa,其稳定趋势斜率K=0.58～0.65。

3 工程应用

板凳山隧洞围岩为粉砂质泥岩,具有风化快、遇水软化、微膨胀等特征,所以对隧洞围岩位移需加强控制。按隧洞初期设计支护方式施作,隧洞收敛值过大,且伴随着初期支护混凝土开裂、喷层剥落。

前文计算的极限支护应力为0.29 MPa,结合试验数据泊松比μ和体积模量G,代入式(11)可计算出隧道允许最大位移量umax=423 mm。考虑到安全系数不低于1.5,本文建议采用型号为18的工字钢,施工间距为0.6 m,其支护应力为0.57 MPa,实际安全系数为1.97,在满足安全的前提下也满足了经济方案,绘制变更后的支护应力曲线如图12所示。

图12 围岩特征曲线Fig.12 The support characteristic curve

支护变更后,通过式(8)可计算出塑性半径,二台阶开挖塑性半径为13～19 m,R/r0=2.17～3.17,但塑性半径仍然较大,为进一步降低塑性区半径,本文研究建议采用三台阶开挖法以进一步减少塑性区半径。通过专家评估并变更施工方案后,选取10 m作为试验段,并在此断面安装压力盒、钢筋计和锚杆计对围岩进行监测,如图13所示。

图13 试验设备安装Fig.13 Installation of test equipment

因粉砂质泥岩具有微膨胀性等特点,需对围岩位移进行重点监测,监测位移曲线如图14所示。将原设计的两台阶开挖法修改为三台阶开挖法,将钢拱架支护间距由0.7 m改为0.6 m,钢拱架型号保持不变后,带来的收益效果为初期支护的收敛位移降低了17%～23%,且解决原设计中出现的混凝土剥落问题。采用三台阶开挖法,钢拱架型号采用20a,钢拱架支护间距改为0.6 m后,初期支护位移增加了15%～24%,但每米节约钢材185.6 kg。综合现场监测的拱架受力以及本文所计算的隧洞最大允许变形量分析,变更后三台阶I18×0.6 m的方案是安全且经济的。将隧洞支护参数及拱架变形数据进行整理,如表2所示。

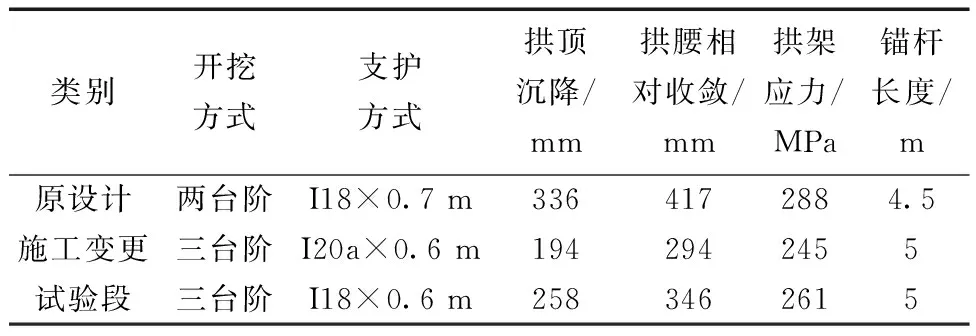
表2 拱架位移对比Table 2 Comparison of arch displacement

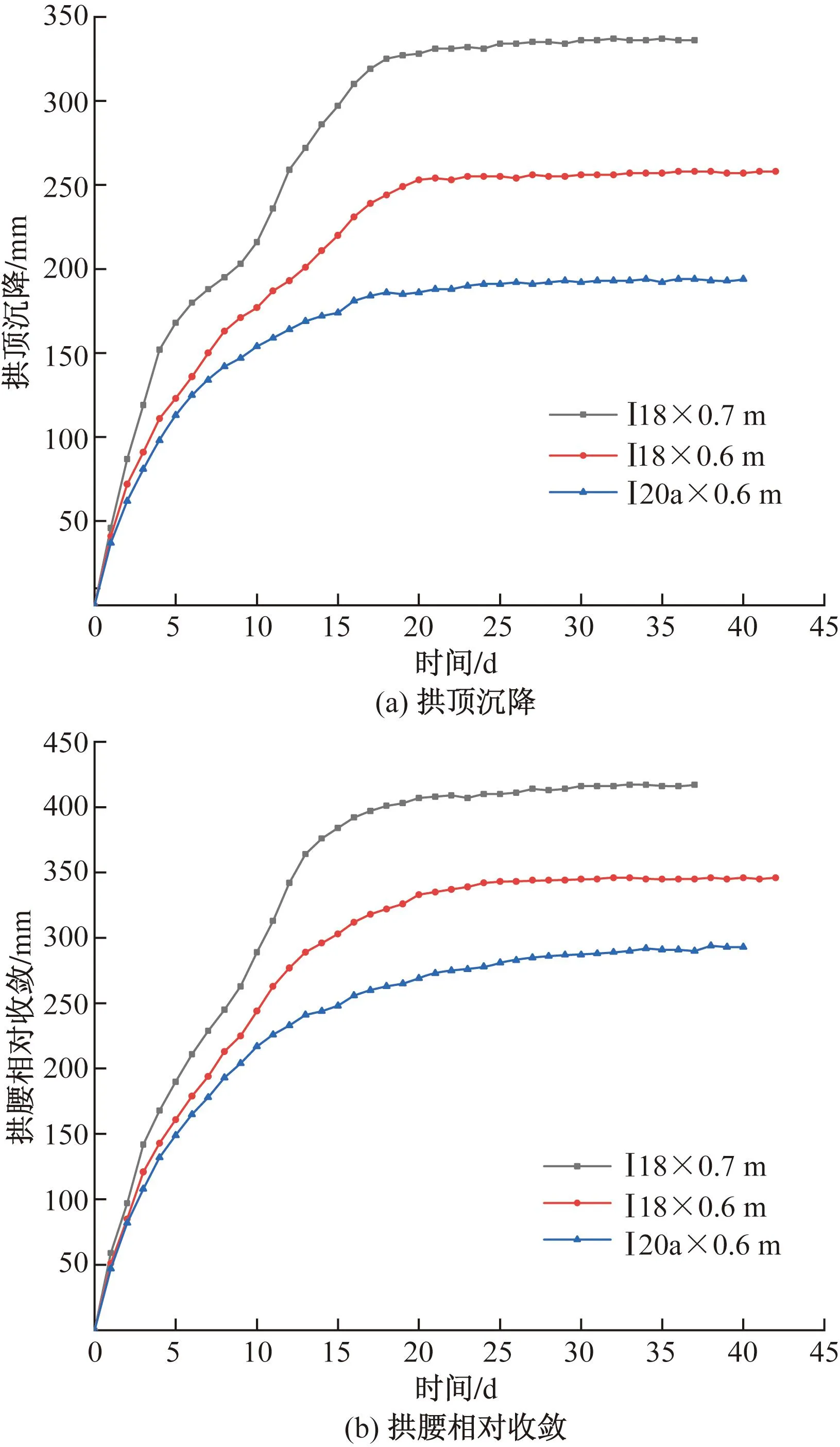
图14 位移对比曲线Fig.14 Displacement contrast curve

本文研究对双向不等压圆形隧道塑性半径计算式进行推导,结合滑移剪切模型对隧洞的极限位移量和极限支护应力进行计算。依托板凳山隧洞进行验证,塑性半径计算结果符合岩石力学经验范围;结合滑移剪切模型对具有微膨胀性的粉砂质泥岩进行极限位移计算,实际位移值略大于计算结果,提升安全系数后的支护参数更为合理,通过隧洞试验及监测验证了变更后支护参数的可行性。