基于功率谱密度与随机配置网络的低压串联电弧故障检测
2024-01-12李金杰邹国锋魏良玉王玮傅桂霞
李金杰, 邹国锋, 魏良玉, 王玮, 傅桂霞
(山东理工大学电气与电子工程学院, 淄博 255049)
随着中国电力网络规模的不断扩大,低压系统设备数量和类型不断增加,绝缘老化、接触松动等原因导致电弧故障,进而诱发电气火灾的概率大大上升[1]。按照发生位置不同,电弧故障分为串联电弧、并联电弧和接地电弧。现代电气故障检测与保护设备已能够较好地实现并联和接地电弧的隔离保护[2],但串联电弧发生时,线路电流受下游负载影响而表现出多样性,且电流幅值与正常线路电流相近、区分度较小,导致故障检测难度极大。另外,由于电弧发展过程是动态变化的,因此每个工频周期的电弧故障都展现出随机性特点,进一步增加了电弧故障特征提取和检测的难度。因此,串联电弧故障的有效特征提取和可靠检测成为电弧故障检测领域的热点和难点之一。
基于电气量的电弧故障检测通过分析线路电压或电流特征实现故障辨识。但由于串联电弧发生位置难以确定,因此电压检测法应用难度较大,电流检测法成为主流研究方向。目前,已有的电流检测法可归纳为阈值比较法和机器学习法两类。其中,阈值比较法是借助时域[3]、频域[4-5]和时频域[6-7]工具对电流信号进行分析,通过比较正常信号和故障信号的特征差异,确定阈值实现电弧故障检测[8]。该类方法计算复杂度低,但阈值难以确定,检测准确率不高。机器学习法是基于智能学习算法自主学习电流特征,并通过支持向量机、神经网络等辨识模型实现电弧故障检测[9-14]。该类方法突破了手动故障特征提取和阈值选取的局限性,受到研究者的青睐。
尽管智能学习算法实现了电流特征的自主学习,但所得特征的物理意义并不明确,可解释性差,因此无法有效建立特征值与电弧电流波形非平稳、随机等特点间的关联关系。针对该问题,本文研究提出一种频域分析与机器学习算法相融合的串联电弧故障检测方法。在电弧电流特征提取中,本文研究采用功率谱密度(power spectral density, PSD)[15-17]对电流信号进行定量化描述,该方法能有效增强电弧电流与正常电流特征的区分度,且所得特征能体现电弧故障的随机性特点。在电弧故障辨识中,本文研究采用随机配置网络(stochastic configuration network, SCN)[18-20]作为故障检测器,该方法能有效克服传统神经网络结构难以确定,网络最优配置需要大量重复实验的缺点[11-12],可真正实现网络模型与电弧电流特征的自适应关联,提升智能辨识模型学习的快速性和检测结果的准确性。
综上所述,现提出融合功率谱密度和随机配置网络的串联电弧故障检测方法。首先,基于UL1699标准搭建串联电弧发生平台,采集线路电流数据,构建数据集。其次,采用Welch法PSD对电流信号进行定量化频域特征描述,构建电弧电流和正常电流特征向量集。然后,基于训练特征集自适应学习SCN网络结构,获得最优网络配置。最后,通过与其他方法的比较实验进一步证明本文方法的有效性。
1 串联电弧故障检测总体流程
现有研究通过对电弧故障电流或电压数据进行分析,提取信号的特征构建电弧电流和正常电流特征向量集进行检测,其检测流程如图1所示。
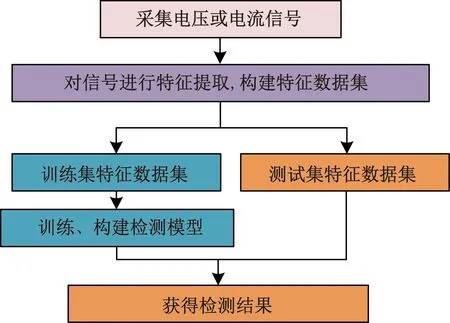
图1 串联电弧故障检测流程图Fig.1 The flow chart of series arc fault detection
与基于电压波形的检测方法相比,基于电流波形的检测方法通过在线路上游安装监测点即可实现对下游支路的电弧检测,具有更强的适用性和灵活性,更受研究者的青睐。因此,首先通过实验采集线路的电流波形。然后对其功率谱密度特征进行分析,构建电流特征向量集。最后以电流特征向量集为输入训练SCN的网络模型,实现串联电弧故障的有效检测。
2 基于功率谱密度的故障特征提取
电弧故障发生时,线路电流与正常电流区分度较小,且电弧故障具有随机性,现有频域分析法难以提取有效的故障判别特征。因此,提出了基于随机信号分析中的PSD算法对随机性电弧电流信号进行定量化描述,通过自相关函数统计信号整体的功率特征,增强电流特征的判别力。
PSD定义了电流信号的功率随频率的变化情况,可以直观地观察功率与频率的映射关系。假设电流信号为x(n),n=0,1,…,N-1,其中N为采样点总数。则电流的功率为
(1)
此时,采用周期图法计算PSD,即
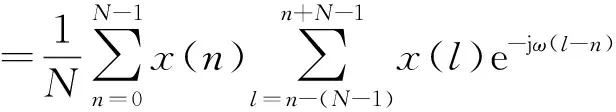
(2)
式(2)中:ω为角频率;l-n为离散傅里叶的时间差,用于求取x(n)的离散傅里叶变化F(f);f为频率。
上述方法计算PSD值虽然简单,但无法在保证较高分辨率情况下尽量减少方差,当信号采样时间较长时,分辨率会降低。因此,研究者采用Welch法改善经典PSD的不足,通过对数据进行分段加窗处理,在保证分辨率的前提下,尽可能减小方差。该方法减少计算量和所需的核心存储量的同时,还能提高信噪比,适合处理数据量庞大、随机性强的电弧故障信号。Welch法流程如图2[17]所示,其计算公式为

图2 Welch方法流程图Fig.2 The flow chartof Welch method
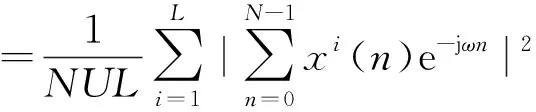
(3)
式(3)中:U为窗函数;L为分段的个数;xi(n)为第i个窗口在x(n)上的样本值序列;Fi(f)为xi(n)的离散傅里叶变换。
显然,在Welch法中所加窗口的窗函数类型、窗口大小,以及窗口间的重叠长度会对特征提取效果产生一定影响,因此在4.2.1节,结合电弧电流数据的消融实验,详细讨论了Welch法中相关参数的设置。
3 基于随机配置网络的电弧检测
随机配置网络实现了对浅层神经网络的有效改进,提升了网络模型学习的自适应性,在一定程度上建立了数据与模型间的关联关系。在SCN中,隐含层节点的选取具有较强的灵活性,节点数量将随着训练的深入和样本数量的增多而自适应增加。当满足最大节点数目Lmax或可容忍误差tol的任一停止条件时,随机配置网络将停止训练,输出最优模型和参数配置。显然,SCN网络训练灵活,不需要大量的重复实验来试探最优网络结构,模型训练效率大大提升。另外,由于所得网络结构与数据密切关联,所以辨识同类型数据的准确率较高。
3.1 随机配置网络的原理
SCN由输入层、隐含层、输出层组成,其结构如图3所示。设电流信号的PSD特征向量集X=[x1,x2,…,xn]为输入样本,输出矩阵为F=[f1,f2,…,fm],gl=[gl,1,gl,2,…,gl,n]为隐含层第l个节点的输出,则SCN的原理[18]描述如下。
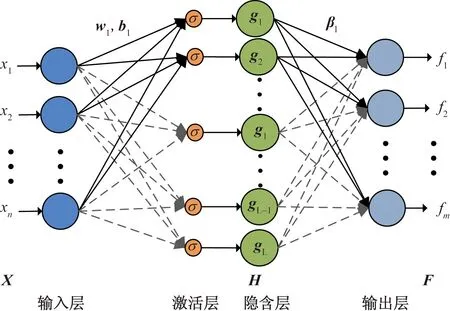
X为输入矩阵;σ为激活函数;H为隐含层矩阵;F为输出矩阵;wl、bl、βl、gl为第l个隐含层节点的输入权重、输入偏差、输出权重、输出向量图3 标准SCN模型Fig.3 Standard SCN model
(1)f:d→m,假设已经构造了一个具有L-1个隐含层节点的SCN,其输出为
(4)
wl=λ[2rand(n,Tmax)-1]
(5)
bl=λ[2rand(1,Tmax)-1]
(6)
式中:F0=0;σ为Sigmoid函数;βl=[βl,1,βl,2,…,βl,m]T为输出权重;λ=[υmin∶Δυ∶υmax]为尺度函数;Tmax为最大随机配置次数;wl和bl分别为第l个节点的输入权重和偏差,在[-υ,υ]d和[-υ,υ]中随机分配。
(2)SCN的残差为
eL-1=f-FL-1=[eL-1,1,…,eL-1,m]
(7)
(3)设立不等式(8)的监督机制ζL对wl和bl进行赋值,以满足网络的通用逼近性质,即
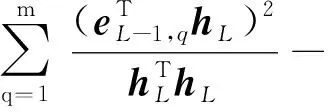
(8)

(4)采用全局最小二乘法,求得最优输出权重为

(9)
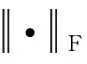
(5)增加新的隐含层节点gL(wL,bL),直到eL-1小于容忍误差tol,或L达到设置的最大节点数目Lmax时停止训练,输出最终模型。
3.2 随机配置网络的训练
SCN训练前需要设定停止条件tol和Lmax,并设定L、W和b分别存储隐含层节点数目、输入权重和偏差,其训练过程如图4所示。
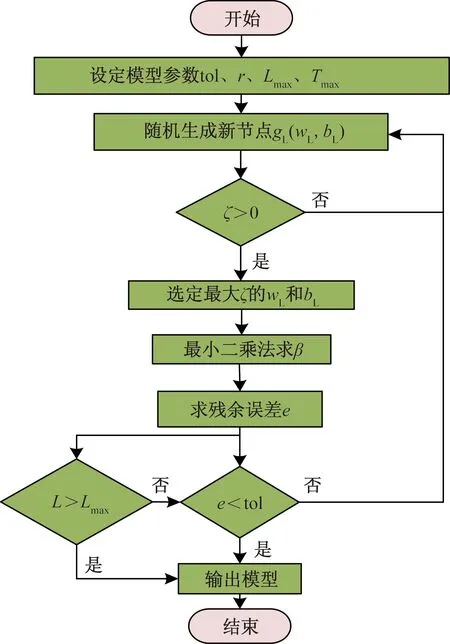
图4 SCN算法流程图Fig.4 Flow chart of SCN algorithm
SCN根据X的特征随机配置wl和bl,训练过程中的学习参数r、尺度函数λ以及最大配置次数Tmax会对网络的学习过程产生影响。
(1)学习参数r。随着SCN训练深入,模型残差呈变小趋势,而网络参数wl和bl随机配置的难度会逐渐增大。因此,学习参数r应按照递增序列逐渐逼近1,以减小对随机配置过程的约束。
(2)尺度参数λ。由式(4)和式(5)可知,参数wl和bl在[-υ,υ]d和[-υ,υ]间随机配置,虽然随机性有利于gL的快速配置,但在SCN训练过程中,随着参数r的不断更新,尺度参数λ取值也应逐渐变化,从而进一步改善网络的训练时间。
(3)随机配置的最大次数Tmax。Tmax控制随机函数候选池的大小,决定网络检测的效率和正确率,应结合数据的复杂程度权衡选择,以返回最大ζL和最合适的wl和bl。
综上分析,将功率谱密度提取的电流信号的频域特征作为SCN的输入,通过调整部分网络参数实现网络结构的自适应学习,并输出最优网络配置。避免了手动调整隐含层节点的大量重复实验,有效缩短了训练时间。
4 实验与分析
4.1 电弧电流数据的采集
基于UL1699标准,本文研究搭建了串联电弧故障发生平台,如图5所示。电路输入电压为220 V工频电压,使用带宽200 kHz的LPCT捕获回路电流,通过示波器记录电流数据。

图5 串联电弧发生平台Fig.5 Series arc generating platform
为综合分析线路下游负载对电路电流的影响,获取多样性的电弧电流数据,实验中选用阻性、开关电源、阻感性、感性电动机4 类负载,以及4 类负载构成的组合负载进行实验,负载类型如表1所示。其中,800 W/400 W电炉、电脑、电磁炉和吸尘器均为低压系统的常用家电,具有典型性。
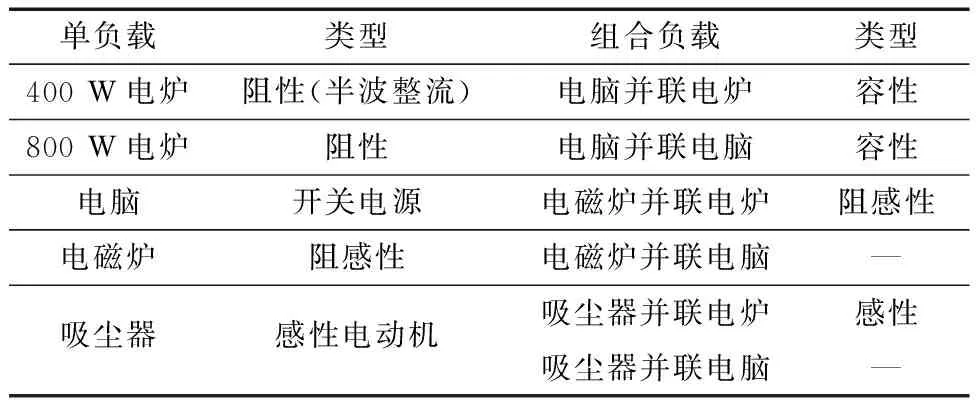
表1 不同负载类型Table 1 Different load type
部分负载电流波形如图6所示,前5个周期为正常电流波形,后5个周期为电弧故障电流波形。显然,电弧故障发生后,电流波形出现不同程度的零休、高频毛刺和电弧故障随机等特点。
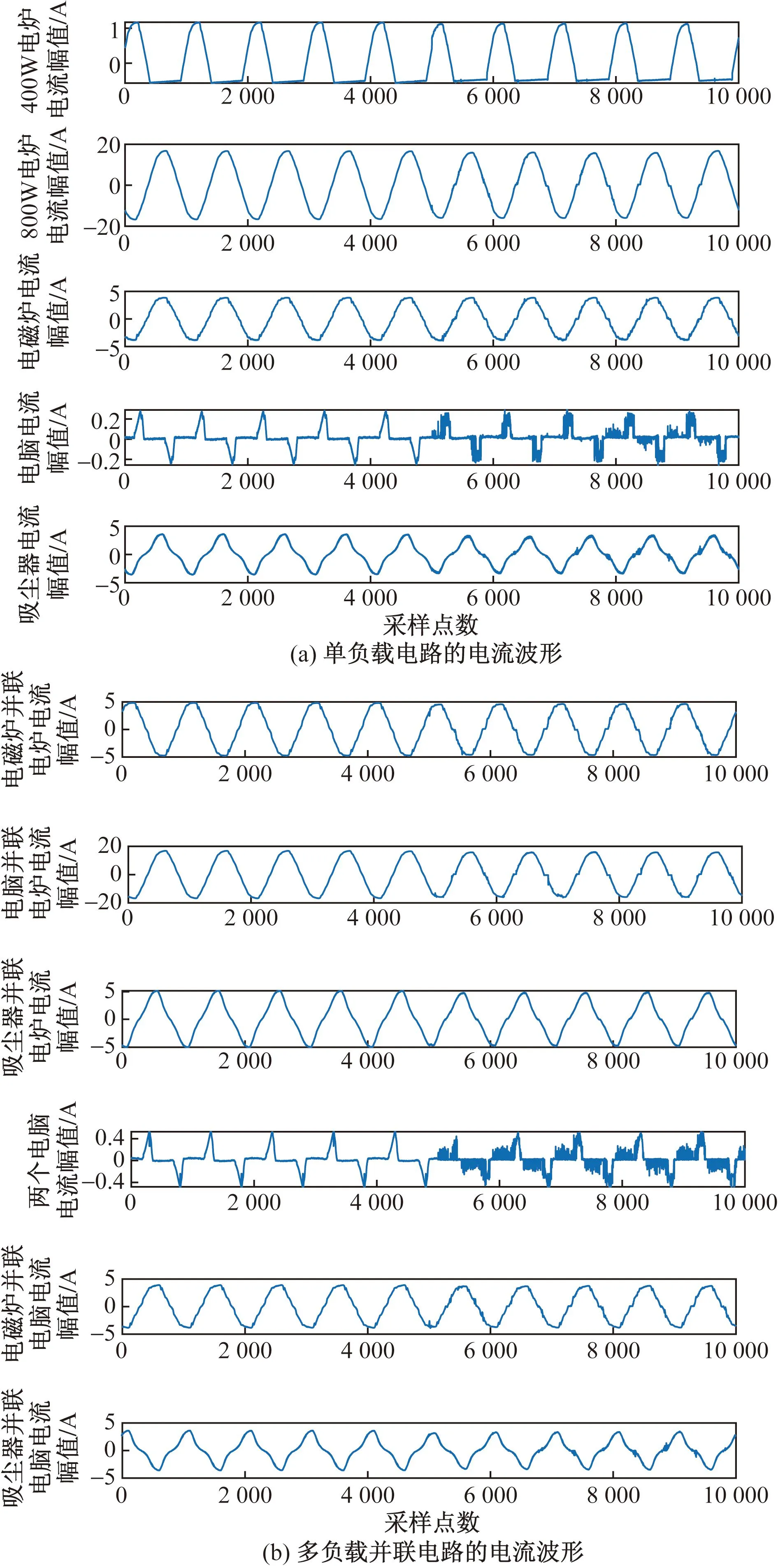
图6 不同负载的故障电弧电流Fig.6 Fault arc current under different loads
4.2 电弧故障特征提取实验
4.2.1 PSD算法参数影响分析
PSD算法的影响因素主要包括窗函数类型、窗口大小和窗口重叠度,优异的参数设置可有效提升所得频域特征的区分度。因此,首先开展了PSD算法参数影响的消融实验,以获取电弧故障特征提取的最优参数配置。
1)窗函数的选取
常用窗函数有矩形窗、凯瑟窗、切比雪夫窗和汉宁窗。其中矩形窗和凯瑟窗分辨率高,但频谱泄露严重,适合对信噪比高的信号做精确估计。切比雪夫窗和汉宁窗在信号频率附近不受噪声影响,但分辨率低,适合对信号做粗略估计[19]。在重叠长度为0、窗口大小为512时,选用4 种窗函数对吸尘器并联电脑负载下的电弧电流执行PSD分析,结果如图7所示。
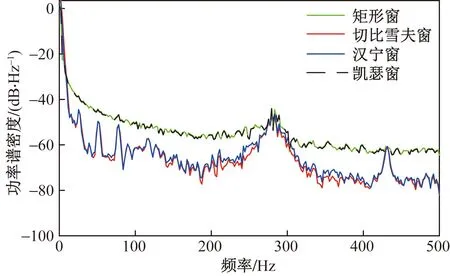
图7 不同窗函数下PSD曲线Fig.7 PSD curve under different window functions
结果表明,采用4种窗函数处理所得波形的分辨率几乎相同,但矩形窗和凯瑟窗的平滑度高,因此两种方法的噪声水平较高;切比雪夫窗和汉宁窗的信号波动大,保留了信号的频谱特征,且汉宁窗的噪声水平更低,因此更适合电弧电流信号的PSD分析。
2)窗口大小的选取
窗口大小N对波形分辨率和谱估计准确率有一定影响:当N取值越大,波形分辨率越高,谱估计越准确;反之,准确率较低。在确定汉宁窗基础上,设置重叠长度为0,分别开展窗口大小为2 048、512、128时电弧电流的PSD特征提取,结果如图8所示。
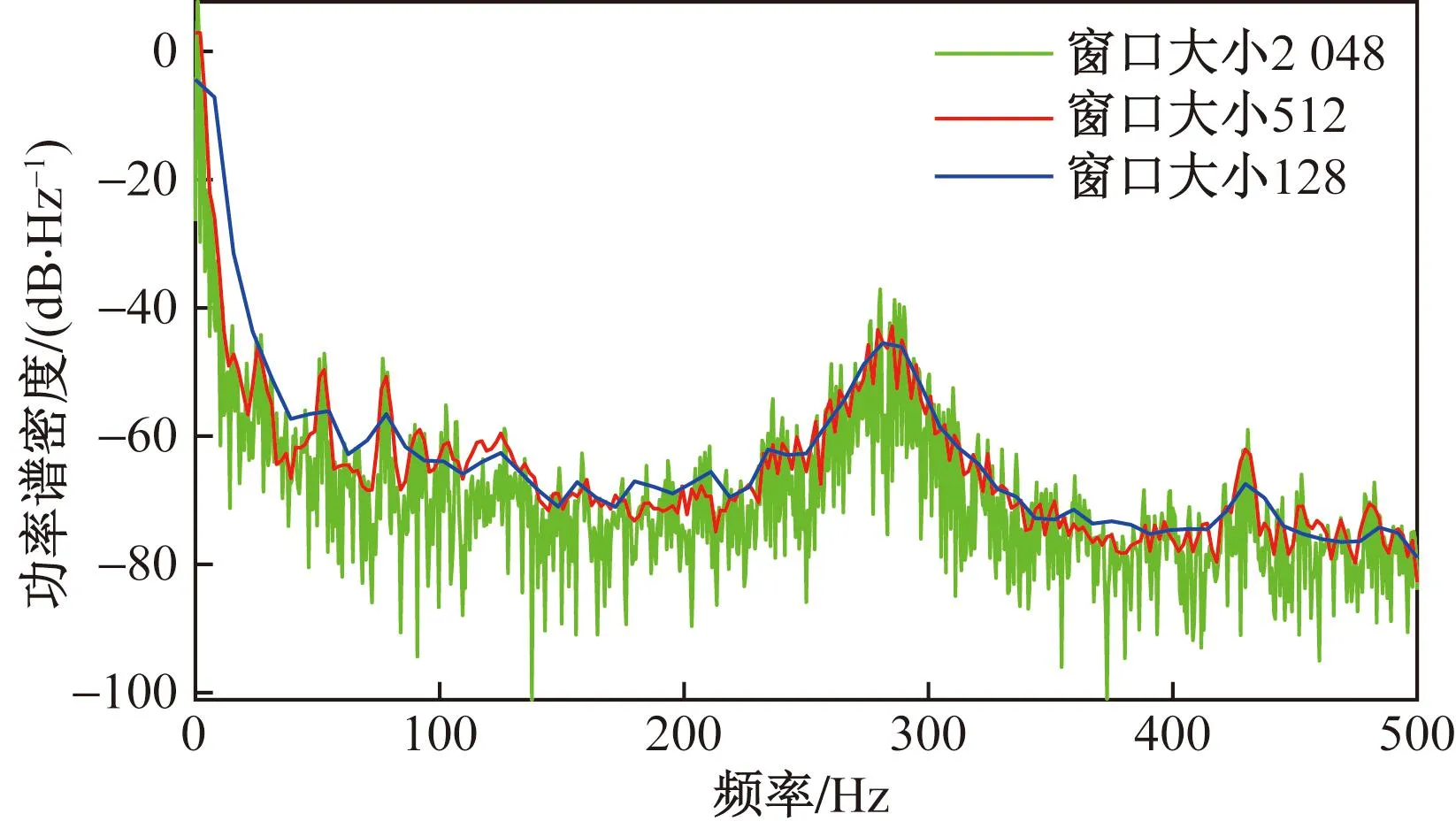
图8 不同窗口大小下PSD曲线Fig.8 PSD curve under different window sizes
结果表明,3种窗口大小的曲线趋势一致,说明PSD消除了频率分辨率影响,但波形分辨率和方差差异较大。当N=2 048时,波形分辨率最高,但存在大量毛刺;N=512时,波形分辨率较高,且较为平滑;N=128时,波形分辨率低,仅部分显著特征得到保留,特征丢失较多。综合分析,N=512时的波形分辨率和方差适中,波形较平滑,判别特征得以有效保留。
3)重叠长度的选取
窗口重叠长度主要影响谱估计的运算时间和波形平滑程度。重叠长度越高,特征曲线越平滑,但谱估计运算量越大。分别开展了重叠长度为0、200、511时的PSD实验,结果如图9所示。显然,3种重叠长度下电弧电流信号的PSD波形平滑程度非常相似,因此应重点考虑节省运算时间,所以重叠长度设置为0,即窗口间无重叠。

图9 不同重叠度下PSD曲线Fig.9 PSD curve under different overlap degree
4.2.2 电弧电流特征提取
特征提取实验中均设置窗口类型为汉宁窗、窗口大小512,重叠长度0。按照纯阻性、容性、感性、感性电动机负载和组合负载的划分进行电流信号特征提取,实验结果如图10所示。

图10 不同负载下的功率谱特征图Fig.10 PSD feature under different loads
实验结果表明:
(1)纯阻性负载。图10(a)表明,电弧故障发生后,电流PSD幅值显著增大,PSD曲线整体向上升高。曲线在100~400 Hz频段抬高幅度最显著,其原因在于阻性负载下,电弧故障给电路电流引入了100~400 Hz的谐波分量。当频率达到500 Hz,正常电流PSD值低于-60 dB,而电弧故障电流的PSD值高于-60 dB,区分度较为明显。
(2)容性负载。如图10(b)所示,串联电弧故障给容性负载电路电流带来大量高频噪声,使频率大于150 Hz后的PSD曲线明显升高。频率达到500 Hz时,正常运行电流的PSD幅度低于-60 dB,而电弧故障电流的PSD幅值高于-60 dB。
(3)感性负载。如图10(c)所示,故障电流与正常电流的PSD值在0~40 Hz、400~500 Hz范围区分度不明显,40~400 Hz间有明显区分。当频率升至500 Hz,正常电流的PSD幅值低于-75 dB,电弧故障电流的PSD幅值高于-75 dB,但区分度不高。
(4)感性电动机负载。如图10(d)所示,感性电动机正常运行时回路电流存在大量谐波,发生故障后谐波含量增大,同时引入少量高频噪声,因而0~280 Hz和400 Hz后故障电流的PSD略高于正常电流。当频率为500 Hz时,正常电流的PSD值低于-70 dB,电弧故障电流的PSD值高于-70 dB。
(5)混合负载。当电路存在多负载并联时,电路情况较为复杂,正常运行时电路中谐波成分复杂,其PSD曲线如图10(e)所示。100~280 Hz、450 Hz之后的故障电弧PSD曲线略高于正常电流PSD曲线,说明故障后引入了相应频带的谐波分量。当频率达到500 Hz,正常电流的PSD值低于-75 dB,电弧电流的PSD值高于-75 dB。
综上分析,功率谱密度分析能够较好实现正常线路电流和电弧故障电流信号的频域特征提取,在一定程度上达到增加特征区分度、降低原始电流信号维数和克服电弧随机性的目的。但仅基于PSD曲线值,无法确定泛化能力较强的阈值来实现所有负载类型下的电弧故障得检测。因此,本文研究提出以功率谱密度特征为基础,进一步采用SCN学习算法实现功率谱密度值的二次特征提取与融合决策,提升特征判别力和电弧故障检测准确率。
4.3 基于SCN的串联电弧故障检测实验
在电流信号功率谱密度特征集中随机抽取60%作为SCN的训练数据,输入到SCN中进行训练,剩余40%作为测试样本,输入已搭建好的SCN中进行测试。SCN初始化时,设置停止条件tol为0.000 1,采用递增序列设定最大隐含层节点数Lmax=[100, 200, 300, 400,…]。当均方根误差大于tol时,Lmax增大100继续训练,直到满足tol要求停止训练,输出网络模型。
另外,还需设定学习参数r、尺度参数λ和最大配置次数Tmax。实验中,学习参数r取值范围设定在0.9~0.999 999,并选用以下3种递增方式:r1=[0.9,0.99,0.999,0.999 9,0.999 99,0.999 999],r2=[0.9,0.919 999,0.939 999,0.959 997,0.979 996,0.999 999],r3=[0.9,0.951 252,0.952 52,0.953 752,0.9552,0.999 999];λ>0,设置为λ1=[0.5,1,5,25,50,75,100,125,150],λ2=[0.5,1,5,25,50,75,100,125,150,175,200],λ3=[0.5,1,5,25,50,75,100,125,150,175,200,225,250];Tmax分别选取T1=300、T2=500、T3=700。基于以上设置,进行了10 组交叉验证实验,SCN的平均训练耗时和测试正确率如表2所示。
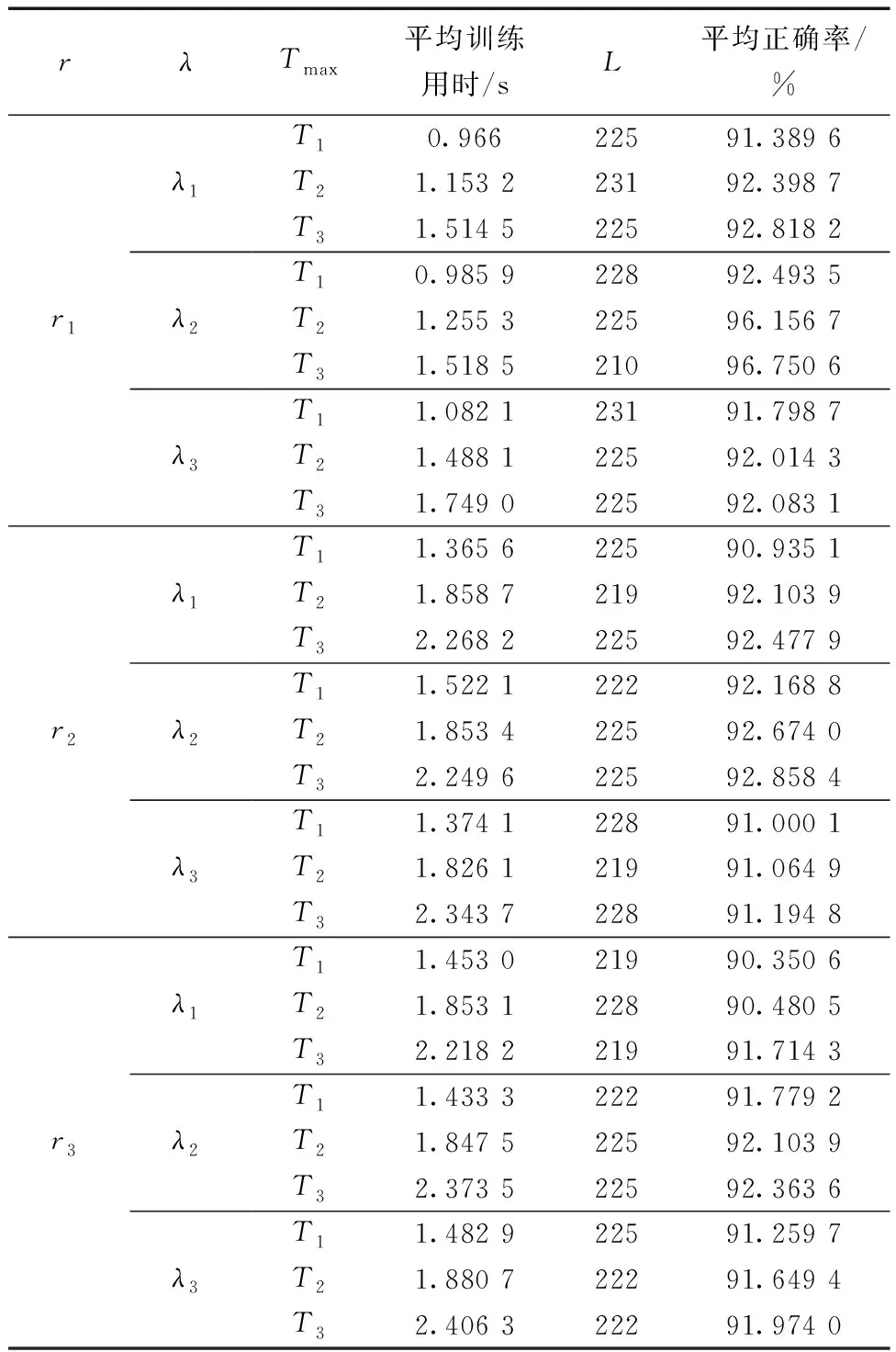
表2 不同参数下测试结果Table 2 Test results under different parameters
实验表明,参数r的递增方式影响网络检测速率和正确率。其中递增方式r1模式下的检测准确率最高。λ的变化主要影响网络训练时间,λ取值范围越大,w和b的选值范围增大,获得符合条件的参数难度增大,网络训练时间加长。而参数Tmax选取过小会导致训练不充分,检测正确率低;取值过大则使训练时间过长,影响训练效率。通过表2可知,当λ=λ2、T2=500时,SCN的综合性能最优。因此,在综合考虑SCN网络训练效率和检测准确率的情况下,最终确定λ2取值方式和T2=500进行SCN的最优搭建。
基于选定参数,SCN训练时网络性能随隐层节点数L的变化曲线如图10所示。随着L的增加,网络训练难度逐渐增大,训练正确率的上升幅度和训练误差的下降幅度逐渐减小,直至满足tol要求时停止训练。图11所示,隐层节点L=50时正确率到达100%,L=210左右时误差达到最小。

图11 SCN的训练过程Fig.11 The training process of SCN
结合表2和图11发现,对网络进行多次训练,每次训练结束的L是不确定的。这是因为输入不同使得网络随机选取的隐含层节点不同,最终导致网络内在结构不同。但受全局最小二乘影响,网络每次增加节点都选择误差最小的偏差和权重,因此隐含层节点数目会稳定在一定范围内。这充分说明SCN能够根据电流数据特点自适应调整网络结构,真正实现了网络结构和电流数据的自适应关联。
综上分析,通过10次交叉验证实验确定了最优参数配置,并实现了网络结构的自适应训练。综合考虑训练效率,基于所得SCN网络模型获得的串联电弧故障检测平均准确率为96.156 7%。
4.4 与其他检测方法的对比实验
为验证本文所提方法的有效性,首先采用PSD和快速傅里叶变换(fast Fourier transform,FFT)、Chirp-Z变换(Chirp-Z transform,CZT)对电流样本进行特征提取,获得不同的电流特征描述。然后与支持向量机(support vector machine, SVM)、随机森林(random forests,RF)、人工神经网络(artificial neural network,ANN)、卷积神经网络(convolutional neural network,CNN)(输入层-卷积层-池化层-随机失活层-全连接层-分类层)等决策模型进行组合,开展了对比实验,从而验证了PSD特征提取和SCN网络的有效性。对比实验结果如表3所示。

表3 对比实验结果Table 3 The comparative experimental results
实验结果表明:
(1)将PSD与FFT、CZT提取的特征向量分别输入到检测模型中进行检测,可以发现,PSD的检测正确率和速率明显高于FFT和CZT。这是因为Welch法PSD可以对随机性的电流信号进行定量化描述,避免了频率分辨率和相位滞后的影响,在减少计算量的同时提高信噪比,提高了电弧故障特征的判别力,改善了检测速率和正确度。
(2)SCN的测试平均正确率与ANN和CNN相差不大,但运行速度明显高于ANN和CNN,略快于SVM和RF,说明了SCN中随机配置隐层节点的有效性。尽管SCN为浅层网络,但网络训练中建立了与电弧电流数据的自适应关联关系,因此具有了良好的特征提取与综合决策性能,且鲁棒性和泛化能力较强,不仅提高了训练效率,还改善了串联电弧故障的检测效果,在自建数据集上的性能优于其他方法。
5 结论
针对低压线路串联电弧故障特征不易提取和故障检测准确率低的问题,提出了采用PSD对电弧电流进行随机信号分析,获得定量化频谱描述,在减少计算量的同时提高信噪比,增强电弧电流特征与正常电流特征的区分度。然后,提出基于SCN的电弧故障检测方法,通过网络自适应学习获得隐含层节点设置,建立网络模型与数据的关联关系,避免了复杂的人工调参,并提升了串联电弧故障检测的准确性。综合运用了频域特征提取与智能检测模型,为串联电弧故障检测提供了新思路。
