柱状颗粒填充床的储能性能分析
2024-01-12郭雪岩
兰 健,郭雪岩
(上海理工大学 能源与动力工程学院,上海 200093)
目前,全球正在大规模发展可再生能源。未来20 年,全球范围内的可再生能源装机总量会每年以2.3%的速度增长。而我国更是在2006 年就已经通过并且实施了《中华人民共和国可再生能源法》[1],以推动可再生能源的发展。可再生能源也有无法避免的劣势——间歇性和波动性,这使得其面临较大的挑战。可再生能源装机容量在发达国家的高速增长对电价市场产生了较大的影响。在一些国家,由于太阳能和风力资源比较充足,进而出现了“负电价”[2–3]。与此同时,由于可再生能源装机容量的增长,基荷电厂需要频繁地进行功率调节,这无疑会损耗其运行寿命[4]。
为保证可再生能源高速、健康发展,需要一种令人满意的技术来储存能量,并将其转化为所需形式的能量。填充床储能是一种很有发展前景的热能储存技术,它具有可降低存储成本和提高太阳能热系统开发效率等优点。储能技术按照储能方式主要分为三种:显热储能、相变储能和热化学储能。顾名思义,显热储能即只通过材料的显热来储存能量,因此材料为非相变材料;而潜热储能则同时利用储能材料的显热和潜热,故其材料为相变材料;热化学储能通过储能材料的反应热来实现能量储存。三种储能方式中,热化学储能的储能密度远大于其他两种,但其系统组成和维护较复杂,使得其在实际应用中有许多的限制,无法发挥其储能密度大的优势[5–7]。而其他两种储能方式中,显热储能的储能密度小于潜热,而相比于热化学储能,潜热储能系统的组成和维护较简单,其在太阳能发电、工业余热利用等相关领域得到广泛应用[8–11]。
储能填充床由储能单元与换热流体组成。在已有换热流体中[12–17],熔盐具有使用温度范围广、成本相对较低等优势。在储能单元方面,对于相变储能填充床,有学者[18–19]使用价格相对低廉且易于获取的石蜡作为相变材料,对储能填充床进行了相关研究,得出了较好的结果。Peng 等[20]利用NaNO2制成的相变胶囊作为储能单元进行了相关研究,其储能性能明显优于石蜡,但由于未与非相变材料形成直接进行对比,无法体现出可量化的优势。同时,有研究者[21]利用陶瓷和石蜡制成了一种多颗粒相变复合材料,研究了不同混合比下储能填充床的性能,在两者之间得到一个较优混合比。Li 等[22]以混合相变材料作为储能单元,分别进行了数值模拟和实验研究。除此之外,Li 等[23]还制作出了两种不同粒径的相变胶囊,将大、小粒径的相变胶囊分层堆叠进行相关研究。大、小粒径相变胶囊的分层堆叠,对换热流体的流动起到了优化作用,同时也可以将大、小粒径的相变胶囊与换热流体的换热进行对比,得出粒径对其换热的影响。
储能填充床实现储能功能主要依靠储能单元与换热流体间的换热以及冷、热流体之间的换热,两部分共同作用使得储能量达到最大。熔盐在中高温填充床储能领域被认为是现阶段最佳换热流体之一。因此,提高储能填充床的性能,需要从储能单元与换热流体间的换热入手。首先,需要考虑的是储能单元的结构。在实际研究过程中,考虑到填充床内储能单元堆积过程中的简易性,研究人员多采用球形储能单元,而圆柱形储能单元则很少被使用,实际上,圆柱形储能单元由于结构上的特殊性,在堆积时有明显的方向性,并且结构上几何元素多,堆积的效果与球形储能单元明显不同。本文基于柱状颗粒建立了一种潜热储能填充床的三维模型,对圆柱与拉西环两种结构储能单元进行相关研究。
1 物理及数学模型
1.1 物理模型
本文填充床使用管径D=30 mm 的圆管,圆管长度为150 mm,其中在进、出口处分别空出30 mm和20 mm,以消除进、出口效应,剩余100 mm为填充段长度,使用Partopour[24]的方法随机填充储能单元。填充床几何模型如图1 所示。在填充床的物理模型生成过程中,为了避免储能单元之间以及储能单元与壁面之间的接触,将储能单元体积减小至其原始体积的99%。本文使用的网格类型为多面体网格,该网格具有较好的适应性。除此之外,在相同的结构下,多面体网格的数量相较于传统四面体网格的更少,在不影响计算结果准确性的基础上,对于计算资源要求更低,网格局部如图2 所示。本研究主要采用结构为圆柱形、拉西环形。本研究中储能单元的相变模型为凝固与熔化模型。该模型中假设相变材料由其他固体非相变材料包裹,其厚度忽略不计。本研究中固体非相变材料为陶瓷,陶瓷在换热过程中不会发生相变,故相变材料发生熔化后不会与换热流体混合。下文中除特殊说明外,圆柱的底面直径与高均为6 mm,拉西环在此基础上孔半径为1.50 mm。

图1 填充床几何模型Fig.1 Geometric model of packed bed

图2 网格局部Fig.2 Local grid enlargement
1.2 数学模型
在本文采用的数值研究中,基于求解器ANSYS Fluent 软件,采用k-ωSST 模型作为湍流模型,使用SIMPLE 算法二阶离散格式对压力速度进行耦合。采用速度入口作为入口边界条件,出口为压力出口,忽略填充床外壁面的散热,故设置其为绝热壁面。本研究使用的流体熔盐[25]密度为1865kg·m-3,比热容为1 510J·kg-1·K-1,导热系数为0.571W·m-1·K-1,黏度为3.22×10-3Pa·s;相变材料为三元熔盐[22],其密度为2 310 kg·m-3,比热容为1540J·kg-1·K-1,导热系数为1.69W·m-1·K-1,潜热为273kJ·kg-1。其中,换热流体为熔盐,相变材料为三元熔盐,其由Li2CO3、K2CO3、Na2CO3分 别 以32%、35%、33%的质量分数制成,其相变温度为668.1 K[22]。
凝固与熔化模型中,其焓值H为显焓h与潜焓 ∆H之和,即
式中:hr为 参考焓值;Tr为 参考温度;cp为比热容;R为 潜热; η为液相分数;T为材料温度 。
η表达式为
式中:Tg为 凝固温度,Th为熔化温度。
1.3 数值模型验证
由于填充床本身无法验证,本文利用Whitaker[26]提出的球体对流传热关联式来验证模拟结果。由于该关联式只针对球体周围的对流换热,而对圆柱与拉西环结构无法直接进行对比,所以采用单个球体的结构来验证数值计算方法的合理性。式(5)为关联式,式(6)为平均努塞尔数计算式,分别为
式中:k为对流换热系数;l为等效球直径; λ为三元熔盐导热系数;Re为雷诺数,其值基于球直径5 mm 来计算;Pr为普朗特数;u∞为主流速度;u0为 入口速度;Num为关联式计算出的努塞尔数;Nu为计算式得出的努塞尔数。
式中:Q为换热量;A为 表面积; Δt为温差。
图3 为利用本文的数值方法基于单个球体得到的计算值与关联式计算值的差别。图中可以看出,在不同雷诺数下,两个方法的努塞尔数差别不大,基本吻合。
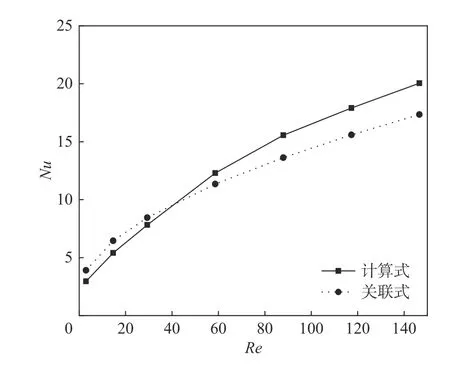
图3 单颗粒努塞尔数与雷诺数的关系验证Fig.3 Relationship between Nusselt number and Reynolds number verified with single particle
本研究中,储能填充床运行温度为573 ~773 K,储能截止温度为772 K,放能截止温度为574 K,均以出口位置储能单元温度为准。储能填充床所吸收/释放能量为填充床进、出热通量绝对值的差值。
2 结果与讨论
2.1 储能单元在储放能过程温度变化规律
在储放能过程中,入口速度均为0.001 m·s-1,填充床运行温度为573 ~ 773 K。图4 为不同轴向位置拉西环温度随时间t的变化。在储能过程中,拉西环储能单元由左往右逐渐熔化。储能结束时间为334.38 s。每个储能单元的储能过程分为三个阶段——固体显热吸热、相变潜热储热、液体显热吸热。在固体显热吸热阶段,储能单元吸收热量后温度升高;在相变潜热储热阶段,相变储能单元因相变潜热吸收大量热量,温度基本不变;在液体显热吸热阶段,相变材料熔化过程结束并且持续吸收热量,温度继续升高。储能过程结束后,储能单元温度保持在773 K。在放能过程中,储能单元由右往左逐渐凝固。该过程与储能过程类似。从图中可以看出,z=40 mm 和z=120 mm 两个轴向位置的储能单元在储能、放能过程中相变潜热阶段的温度变化相对于其他位置均不明显,原因是这两个位置在相应的过程中均处在换热流体的入口附近,换热温差相对较大,从而换热速率较快。在Li 等[23]的数值计算结果中,其潜热吸热(放热)阶段时长随着与进、出口距离的减小而减少,但并未减少到无法明显看出的程度,因为其距离进、出口最近的位置x/H0为0.25(x为填充段到未填充段的距离,H0为填充段总长度),本文中x/H0为0.1,距离进、出口更近;其次,其填充床以及储能单元尺寸远大于本文中的尺寸,潜热阶段所需能量更多,故该阶段时长更长,因此其潜热阶段更为明显。
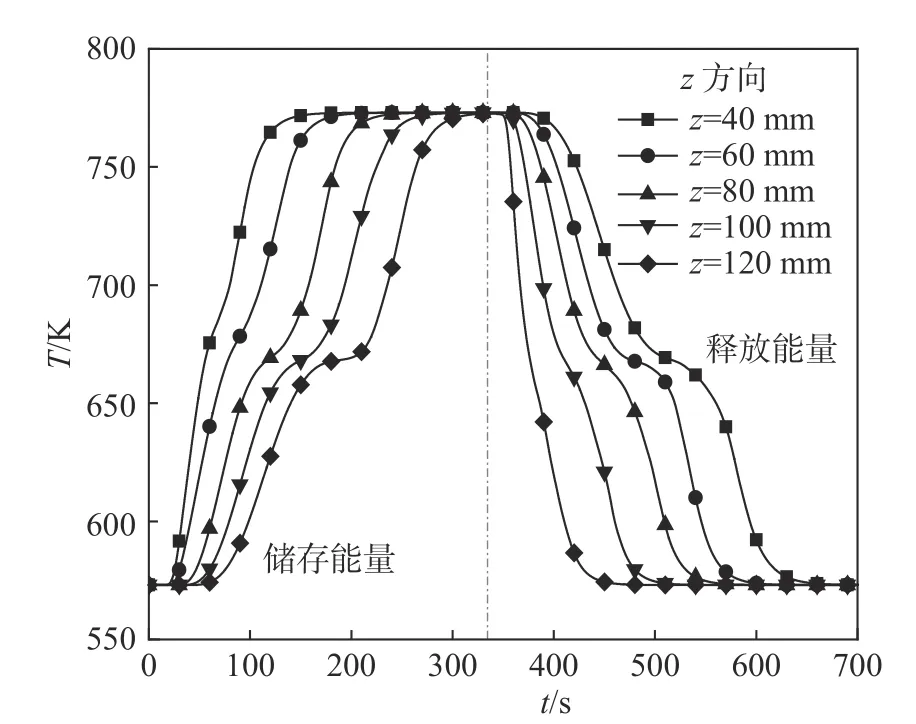
图4 不同轴向位置拉西环温度随时间的变化Fig.4 Changes of Raschig ring temperature with time at different axial positions
2.2 不同直径比下储能性能
颗粒与填充床的直径比决定了颗粒分布的复杂程度,进而影响填充床内流场的混乱程度。分别研究直径比D/d=3.0、5.0、7.5(d为颗粒底面直径)的拉西环填充床(拉西环高度为6 mm,d分别为10、6、4 mm,孔半径为1.50 mm)。三种填充床堆积模型如图5 所示。

图5 不同直径比下填充床堆积模型Fig.5 Packing models with different diameter ratios of bed to particle
图6 为不同直径比填充床z=80 mm 处储能单元温度随时间的变化和填充床的储能时间和储能量。三种填充床空隙率分别为0.59、0.60、0.77,储能速率分别为167.18、240.76、267.66 W。三种填充床的储能量、储能时间与空隙率均成反比。综合考虑储能时间与储能量,填充床的储能速率随着空隙率的增大而增大。直径比为7.5 的填充床储能单元数量多,且孔半径与拉西环底面直径比大,故其换热面积大。在前75 s 左右,由于换热速率高,前段储能单元吸热量多,在填充床中段的换热温差较小,则前期该处储能单元升温慢。75 s 后,三种填充床前段储能单元均换热充分,中段温差基本一致,对于直径比为7.5 的填充床,其储能单元换热面积大,温度快速上升。
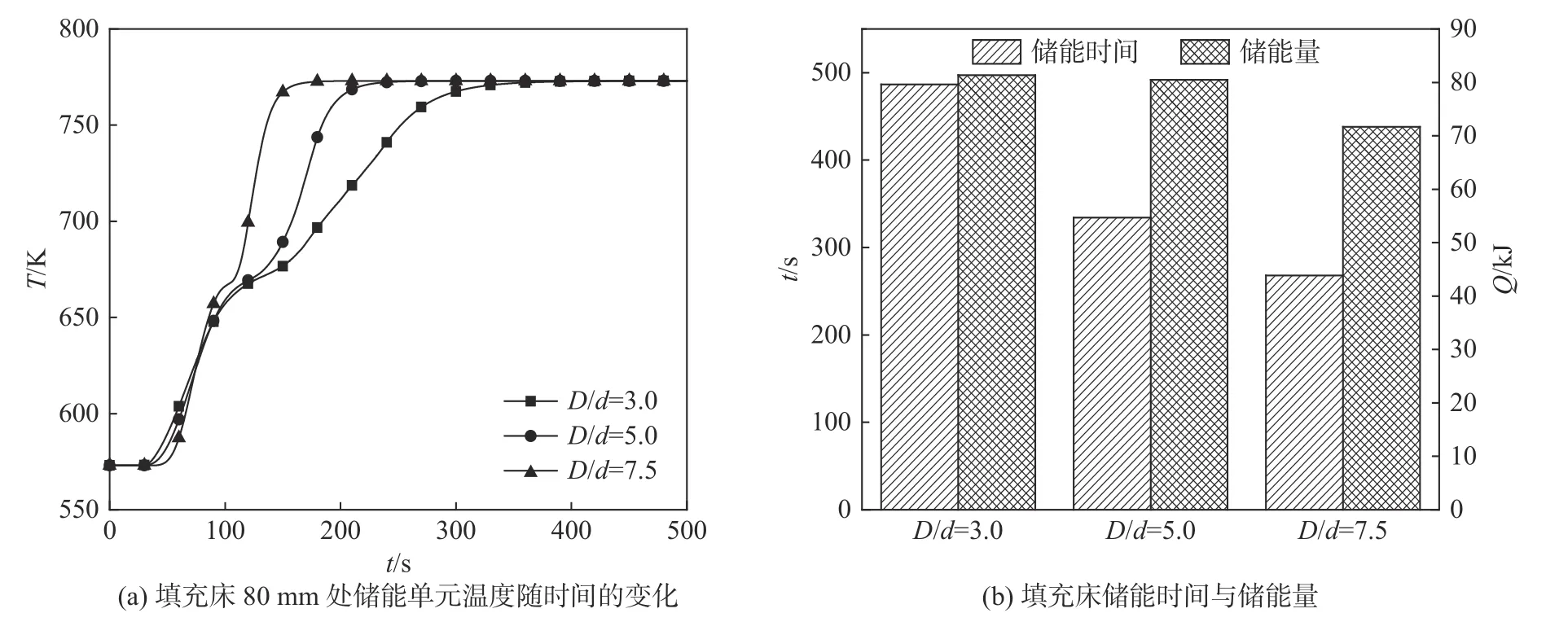
图6 不同直径比下填充床的储能过程及储能性能Fig.6 Energy storage process and performance of packed bed with different diameter ratios of bed to particle
2.3 不同储能单元结构下储能性能
2.3.1 不同圆柱高度下储能性能
圆柱储能单元的高度会直接影响100 mm 的填充段中储能单元的个数以及分布,进而影响填充床的流场。因此,对由高度h分别为3、6、9 mm 的圆柱储能单元(底面直径均为6 mm)组成的填充床进行研究。不同圆柱高度下填充床堆积模型如图7 所示。

图7 不同圆柱高度下填充床堆积模型Fig.7 Packing models under different cylinder heights
图8 为不同圆柱高度填充床z=80 mm 处储能单元温度随时间的变化与填充床的储能时间和储能量。随着圆柱高度的增大,储能量基本呈降低的趋势,三种结构填充床填充段的空隙率分别为0.479、0.484、0.495,储能速率分别为228.73、204.77、204.75 W,这意味着高度为3 mm 的填充储能单元所占体积最大,而单位体积下储能单元所能储存的能量比换热流体的大,因此高度为3 mm 的填充床储能量最多。如果将储能量与储能时间的比值作为储能速率,则储能速率随着孔隙率的增大先减小后基本不变。由圆柱高度为3 mm 的颗粒组成的填充床储能单元个数多,换热面积大。前期储能单元换热速率较高,前段储能单元吸热量大,则中段储能单元换热温差小,因此前期该处储能单元升温慢。之后,三种填充床前段储能单元均换热充分,中段温差基本一致,对于圆柱颗粒高度为3 mm 的填充床,其内部换热面积大,温度上升较快。

图8 不同圆柱高度下填充床的储能过程及储能性能Fig.8 Energy storage process and performance of packed bed with different cylinder heights sizes
2.3.2 不同拉西环孔半径下的储能性能
通过改变拉西环孔半径可在保持储能单元数基本不变的情况下改变填充床的空隙率,进而影响填充床内部的换热。因此,对孔半径r分别为0.75、1.50、2.25 mm 的拉西环(拉西环底面直径和高度均为6 mm)组成的填充床进行相关研究。三种孔径下填充床堆积模型如图9 所示。

图9 不同孔半径下填充床堆积模型Fig.9 Packing models under different pore sizes
图10 为不同孔半径填充床z=80 mm 处储能单元温度随时间的变化和填充床的储能时间与储能量,其中孔半径为0 表示圆柱储能单元。四种填充床空隙率分别为0.48、0.52、0.60、0.77,储能速率分别为204.77、211.12、240.76 、219.50 W,对比孔半径为0、0.75 mm 的储能单元组成的填充床,发现孔半径为0.75 mm 的换热面积大,换热速率高,则在储能截止时间时,末段颗粒与出口之间的换热流体温度高于孔半径为0 的填充床,因此0.75 mm 的填充床储能量较大。同样的,孔半径为1.50、0.75 mm 的填充床也有这种情况,但孔半径为2.25 mm 的填充床中储能单元的体积占比过小,这部分能量小于储能单元之间能量差,所以孔半径为1.50 mm 的填充床储能量较大。就储能速率而言,由孔半径为1.50 mm 的拉西环组成的填充床储能速率最高。
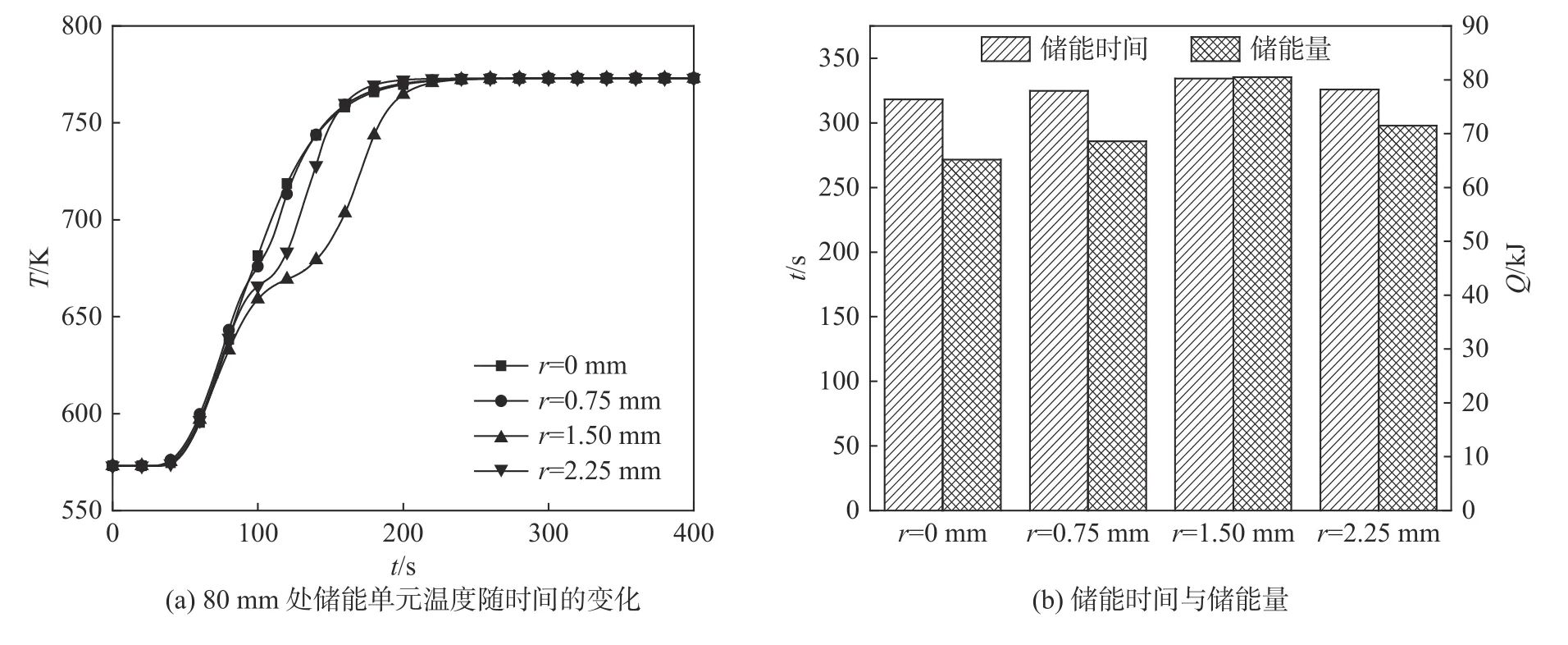
图10 不同孔径下填充床的储能过程及储能性能Fig.10 Energy storage process and performance of packed bed with different pore sizes
3 结 论
采用数值模拟方法分别对圆柱和拉西环结构储能单元组成的填充床进行相关研究,采用储能时间、储能量来表示填充床性能,分析了填充床直径比与储能单元结构参数对填充床性能的影响,得出如下结论:
(1) 随着填充床直径比的增大,储能速率逐渐加快。具体而言,直径比为7.5 的填充床的储能单元个数约为直径比为3 的填充床的个数的7.4 倍。相较于直径比为3 的填充床,直径比为7.5 的填充床储能时间减少了45.0%,但同时储能量仅减少了11.9%,综合两点考虑,其储热速率提高了60.1%。
(2) 圆柱储能单元高度的增加对填充床储能量的影响较小,储能时间先增加后基本不发生变化,综合而言,储能速率先减小后基本不变,所以在圆柱高度研究范围内,高度为3 mm的圆柱组成的填充床储能速率最高。
(3) 随着储能单元孔径的增大,储能量呈先增后减的趋势,但储能时间相差不大,故在孔径研究范围内,储能速率同样出现先增后减的规律,其中孔径为1.50 mm 的拉西环组成的填充床储能速率最高。
