“双减”背景下的数学教学“教学做合一”的探索

陈亦怡

【摘  要】  本文基于教育实践，对于“双减”大背景，对于数学教学中“教，学，做”三者做思考及实践应用，简述三者合一对于学生学习的助益.

【关键词】  初中数学;“双减”；教做学合一

数学作为初中阶段的重点学科，对于学生来说，难度大，内容多，教师更应该扎实践行“双减”原则，立足于教育质量，在“双减”的指挥棒下，思考探索一条“教学做合一”的新道路来将“双减”教育政策落到实处，真正做到为学生减负提质.

1  初中数学“教学做合一”的必要性

初中阶段，数学对于很多学生来说，是有较大难度的科目.为了突出学生的主体地位，教与学都应以学生的做为核心，学生怎么学教师就怎么教.数学学习的来源是日常的生活，在日常生活当中，处处有数学问题.教师在初中数学教学实践中，完成纵向的知识的梳理，复习课中横向的帮助学生比较不同章节的内容，年末学生学习的时候，就可以构建自己的知识框架网络，从而在解题做题，解决数学问题的环节当中，更加得心应手，“教——学——做”三者是三位一体的，有机的结合可以提升教育的质量，从而达到减少学生负担的目的[1].

2  初中数学“教学做合一”的优势

以往的初中数学课堂，以概念新授、例题讲解、课后习题巩固的模式为主导.学生重复的练习偏多，深度的思考偏少.应该将“教学做合一”推行到日常教学工作中去.将数学教学深深扎根于学生日常生活中碰到的场景，激发学生的学习兴趣，让学生有主动学习的欲望，突出学生主体地位，拒绝填鸭式的直接告诉学生公式定理，而应该启发激励学生自己去探索知识的产生，发展，梳理知识之间纵向的逻辑联系，感受知识之间一以贯之的联系，复习阶段再横向的比较不同的章节的知识，由异同的比较加深学生的理解，帮助学生构建自己的知识网络，从而最后达到能应用知识即“做”的程度.水到渠成的达到教学的目标.顺应学习的发展脉络自然事半功倍，达到减负而提质的效果.

3  初中數学“教学做合一”的应用

3.1  一题多解，横向比较，融会贯通提升质量

陶行知先生有句名言：“行是知之始，知是行之成.”印证到数学学科当中，单道题目的解决，只是数学技能的应用，而此时，对于整个框架只有大概的印象，对于系统的知识结构也不到位，而只有将相关的若干章节结合起来看，横向的比较联系，感受异同，才能加深学生对于数学的理解，融会贯通，形成自己的知识网络.

“教”：在复习课的教学活动当中，可以设计综合题训练.让一道题目涉及多章节内容，杂糅多个知识点.给学生创造一个整合各章节知识点的契机，并给予学生必要的启发协助学生梳理知识采用一题多解的形式，既提升了学生的兴趣，激发学生对数学的钻研精神，也把数学学科综合起来.数学学科本来就是一体的，章节的划分是为了方便学生在初学阶段理解.

“学”：当一道题目涉及多章节内容的时候，对于学生的挑战是较大的.在有一定知识储备之后，学生在“做中学”，在解决问题的过程当中，感受各章节知识点紧密联系.从一开始，不同学生用不同方法解决同一道题目，感受从不同角度解读题目都可以解决数学问题.随着时间的推移，部分优秀学生可以达到一个人能应用不同的方法解决同一道题目.这开拓了学生的思维能力发散学生思维，对学生整体的数学素养形成也很有帮助[2].

“做”：陶行知先生提出的“教学做合一”思想，是以“做”为核心的，做是“学”的核心，也是“教”的中心，它是“真知识”的源泉.“真知识”是由思想和行为结合而产生的知识，必须根植于“做”.

例  以下题第2小题为例

如图1，在平面直角坐标系中，顶点为（3，4）的抛物线交y轴于A点，交x轴于B、C两点 （点B在点C的左侧），已知A点坐标为（0，－5）．

（1）求此抛物线的解析式；

（2）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴l与⊙C有什么位置关系，并给出证明[3].

图1           图2            图3

解法  （1）略y=-x2+6x-5.

（2）分析：先要会把大综合题拆解成小题目，删繁就简转化为熟悉的题型.

这题需要我们判断直线与圆的位置关系，即判断半径及距离的大小问题，距离已知只需求

求垂线段长.

先解距离：令y=0，则-x2+6x-5=0，则x=1或x=5，对称轴x=3，d=3-1=2.

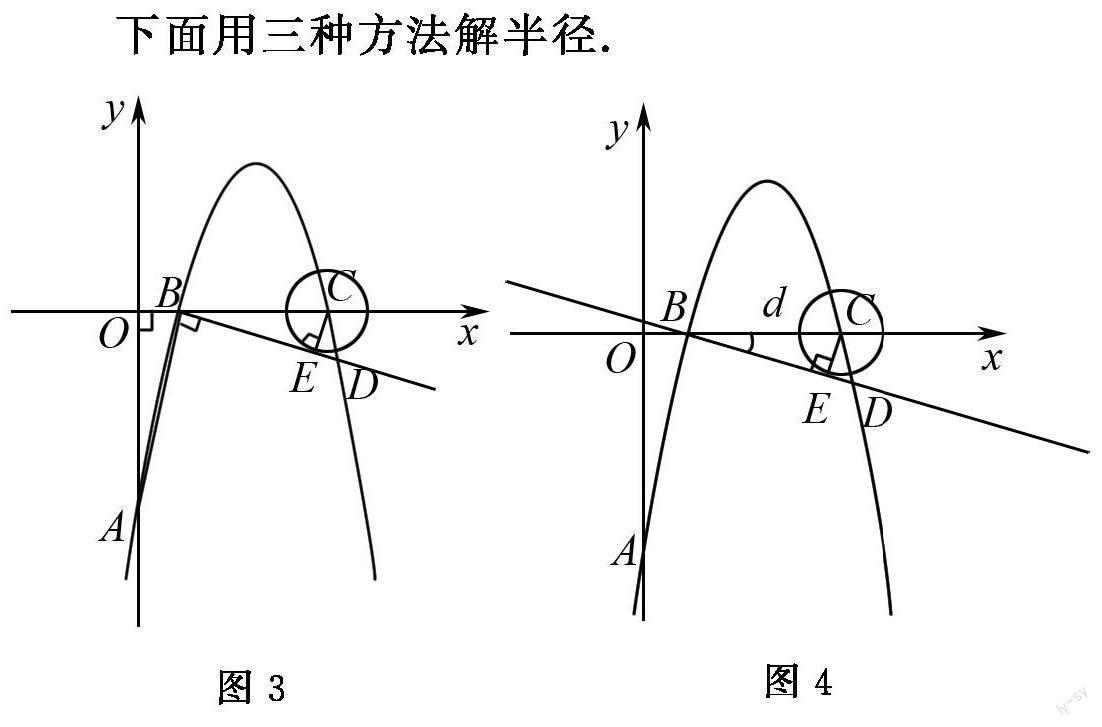
下面用三种方法解半径.

法1  代数角度

思路分析  由相切得出垂直的位置关系，求出直线BE及CE解析式，得出C、E的坐标，得出CE的长，与半径进行比较.

法2  几何角度

思路分析  由K字型相似△OAB～△EBC，得出CE的长，与半径进行比较.

法3  三角函数及解直角三角形角度

图4

思路分析  由解析式的斜率k即为，与直角三角形关联起来，解直角三角形，得到所对的对边CE的长，再与半径进行比较.

横向的一题多解，帮助学生发散思维，各章节横向连接，拓宽思维.

3.2  由易至难，纵向深化，变式思维提升质量

“教”：数学学科会有难度大的题目.于做中教，一方面要自己做题目，精挑细选合适的习题，布置给学生，教师跳下题海，才能让学生不下题海.教师在解题当中也提升了自己的数学能力，有所感悟.另一方面，教师可以通过设置问题串的形式，由易及难过渡，帮助解决难度大的题目，这就要求教师在引导学生们复习的时候，不能单单设置扁平化的习题组，拼凑起难题目的集锦，那样的话效果一般，应围绕几个知识点，由浅及深，展示给学生看，题目是如果一步一步加深难度的，如果以后碰到了难题目，应该如何去思考，将之与以前熟悉的题目知识点联系起来解决.

“学”：当学生已经有相关知识储备的时候，可以进一步加深难度学习.比如通过题组的形式，感受由易到难的过程.形成复杂题目是由已经熟悉的简单题目演化过来的观念，那么就能形成迎难题而上的精神.而变式的题组，不是简单的“外源变式”，仅仅改变数值，位置，字母等，而应该是“内源变式”，隐性条件的增减，限制条件的变化等等.学生在学习的过程中更加能理解，达到在“做中学”的效果.

“做”：当教和学合一，落脚到做的时候，学生在做的过程中，可以打破的教材关于本知识点的结构体系，重新整合题目，提升难度，建立起更加高级的思维结构体系[4] ，数学学习就是要能够利用学习到的知识点来解决问题.很多难度系数大的问题，其实都有题源，所谓万变不離其宗.真正的学习，要会理清思路，感受应用特定的几个知识点可以解决一系列的问题.

例  变式题组

题源  将军饮马问题.据说，在古希腊有一位聪明过人的学者，名叫海伦.有一天，一位将军向他请教了一个问题：从A地出发到河边饮马，然后再B地，走什么样的路线最短？如何确定饮马的地点[7]？

图5                               图6

解法  如图5，①做A关于l的对称点A’；②连接A’B与l交于点P；③P为饮马的地点，最短路线为A----P---B;①.

涉及知识点  ①垂直平分线上的点到线段两端的距离相等；②两点之间线段最短.

变式1  加入动点

如图6，在锐角三角形 ABC 中 AB=，∠BAC=45°，∠BAC 的平分线交 BC于点 D，M、N 分别是 AD 和 AB 上的动点，则 BM+MN 的最小值是（   ）

解法  ①在AC上截AN’等于AN，则△AN＇M≌△ANM，则AN’=AN，则BM+MN的最小值即为BM+MN’的最小值；

②移动N’使得BN’最短，即BN＇与AC垂直的时候.

涉及知识点  ①两点之间线段最短；②垂线段最短.

纵向的梳理题目，要展示题组给学生，引导学生体会他们的本质是一以贯之的.抓住关键点之后，在复杂题目中分析出他的题源是什么，用到的思想方法是什么，从而化繁为简解决题目，也加深了理解.自己脑海中的知识网络也延伸了.

4  合理布置作业，减轻学生负担

作业是巩固学生学习效果的最重要途径之一，做作业也是学习新知识的重要一环.而不合理的作业布置，可能导致学生负担过重，或者重复训练而没有进步.作为教师我们要体谅现在学生们巨大的压力.“双减”既是政府倡导的教育指挥棒，更应该是每个教师发自内心去践行的道路.

通过实践发现，作业分层是一个非常好的方法.符合因人而异，因材施教的原则，做到以学生为主体，学生想学什么，就教什么.有了针对性，那么就可以做到“少而精”.

具体措施是可以出A，B卷.对应的题号的题目，难度不同，但是针对的知识点相同，这样就控制了学生们总的作业量，遵循了“双减”背景下的作业适量的原则.同时也做到了突出重点难点，提升了作业的布置的质量，在可操作的原则之下做到了因材施教，基于学生本人的知识功底及应用的水平，提供了他所需要的训练，符合最近发展区的理论，让学生“跳一跳，够得到”，给学生思维发展及探索发现的机会.最大化作业的效果，培养学生的核心素养.真正以学生为主体，教围绕学生而教，学生们学着做符合他们个人的训练来发展自身，教学做三者合一，提升能力.

5  结语

陶先生的“教学做合一”的思想时至今日仍然极有指导意义，在“双减”的大背景下教师应扎实践行陶先生的指导思想，将理论应用于实际帮助孩子健康快乐的成长.

参考文献：

[1]张连成.高中数学教学中“教学做合一”思想的有效应用探索[J].高考，2022（04）：72-74.

[2]贾永亮.开拓思路 一题多解——谈初中数学一题多解的教学研究[J].数理化解题研究，2021（26）：14-15.

[3]姜重旭.圆在二次函数中更具挑战性[J].数理化学习（初中版），2015（08）：17-19.

[4]孙朝仁.初中数学复习课的思维转型路径——以“一元二次方程”复习课为例[J].中国数学教育，2021（05）：2-5.