政府-平台电商协同监管大数据“杀熟”的演化博弈研究

摘 要： 为有效遏制数字经济背景下平台卖家大数据“杀熟”行为，推动平台经济高质量发展，文中在现有研究基础上，以演化博弈理论为核心，分析了信息不对称情境下政府、平台电商与平台卖家间的利益博弈关系，构建了协同监管激励机制模型.通过引入政府规制，求解政府与平台电商最优惩罚力度、最优激励监管系数以及各主体行为演化方向，讨论大数据“杀熟”监管时各外生变量对各主体最优策略选择的影响，证明了协同监管的优越性与必要性，为网络交易市场监管提供理论参考.

关键词： 数字经济；大数据“杀熟”；演化博弈；数值仿真

中图分类号：X323；F224"" 文献标志码：A"""" 文章编号：1673-4807（2024）06-090-12

收稿日期： 2023-10-12"" 修回日期： 2021-04-29

基金项目： 江苏高校哲学社会科学研究重大项目（2022SJZD080）；江苏省社科基金项目（22EYB001）

作者简介： 王海燕（1998—），女，硕士研究生

*通信作者： 毛昭军（1980—），男，副研究员，研究方向为体系智能、博弈优化.E-mail：24945247@qq.com

引文格式： 王海燕，赵久富，郑雪琪，等.政府-平台电商协同监管大数据“杀熟”的演化博弈研究［J］.江苏科技大学学报（自然科学版），2024，38（6）：90-101.DOI：10.20061/j.issn.1673-4807.2024.06.014.

Research on the evolutionary game theory of government-platforme-commerce collaborative regulation of big data ″killing off″

WANG Haiyan1， ZHAO Jiufu2， ZHENG Xueqi1， ZHANG Na1，MAO Zhaojun^3*

（1.Business School， Nanjing University of Information Science and Technology， Nanjing 210044， China）

（2.Unit 31700， Liaoyang 111000， China）

（3.System Engineering Research Institute， Academy of Military Sciences， Beijing 100091， China）

Abstract：To effectively curb the big data ″killing off″ behavior of platform sellers in the context of the digital economy and promote the high-quality development of the platform economy， this paper， based on existing research and using evolutionary game theory as the core， analyzes the interest game relationship between the government， platform e-commerce， and platform sellers in the context of information asymmetry， and constructs a collaborative regulatory incentive mechanism model. By introducing government regulations， the optimal punishment intensity， optimal incentive supervision coefficient， and evolution direction of each entity′s behavior for e-commerce between the government and the platform are solved. The impact of exogenous variables on the optimal strategy selection of each entity during big data “killing off” regulation is discussed， the superiority and necessity of collaborative regulation proven， and theoretical reference provided for the regulation of online trading markets.

Key words：digital economy， big data ″killing off″， evolutionary game， numerical simulation

平台经济是数字经济的组织形态，引领着数字经济模式和场景创新，成为数字经济发展的新动能和新引擎.但是，虽然平台经济推动了数字经济的急速增长并促进其高度繁荣，但是却带来了新的社会风险问题.平台经济的特征是参与主体众多、交易信息海量、线上线下信息不对称以及网络外部性鲜明，因此传统经济下的市场失灵问题呈现出新的形式，同时也蔓延出比如假冒伪劣产品盛行、网络产业犯罪、“大数据”杀熟等问题，对数字经济和平台经济的监管体系提出了新的挑战^［1］.尤其大数据“杀熟”因其特有的智能化、系统化、批量化、隐蔽性等特点，制约了平台经济的健康发展，成为平台经济可持续发展急需解决的重点问题.因此，如何有效制约大数据“杀熟”现象成为政府、学术届、实业界关注的热点话题.

平台卖家的大数据“杀熟”行为侵犯了消费者的知情权、公平交易权和隐私权，处于电子商务产业链顶端的电商平台应当承担起监管职责，制止平台卖家的“杀熟”行为.但是， 囿于平台电商与平台卖家缔结了组织内委托代理关系，使平台电商一方面要对平台卖家的违规行为进行监督惩戒，同时又要对受到外部指责的平台卖家给予积极的保护^［2-4］.可见，平台交易市场仅通过内部监管还远远不够.为此，政府出台了系列法律条文，明确将涉及消费者切身利益的在线刷单、虚假评论等平台乱象纳入法律监管范围内，以保障网络交易环境与消费者权益.可见，充分发挥政府的导向作用、加强政府监管，对于破解平台电商“监管困境”，形成公平健康的平台交易环境显得尤为重要.但是囿于政府机构的信息劣势和高昂的执行成本，仅政府规制也难以起到预期的效果.因此，构建合理有效的协同监管治理机制，加强政府与平台电商间的互动，对促进平台经营规范化与合法化，推动网络市场高质量发展具有重要意义.

目前学术界关于大数据“杀熟”监管的研究，从研究方法上来说，有较多学者运用博弈论对监管问题展开研究.尤其政府的介入引起了学术界的广泛关注，如：文献［5］建立一对多的政府与企业对称博弈模型，得出加大政府对企业的检查频率、降低企业自律成本有利于规范企业自身行为.文献［6］构建了不完全信息下的三方静态博弈模型，发现企业、经销商和政府监管部门严格规范自身行为与否取决于各自的监管力度、监管成本.文献［7］构建了政府和企业之间的混合战略博弈模型，探讨了双方博弈关系及不同情况下的最优策略选择.事实上，大数据“杀熟”协同监管问题是多个群体随机配对的反复博弈问题，适用于演化博弈分析^［8］.相比传统博弈方法，演化博弈方法在处理监管问题时的优势主要体现在：第一，考虑时序变化，能够从长时期的角度观察分析博弈的动态变化，参与者通过模仿、学习的过程，最终实现各种策略的群体比例达到演化稳定均衡状态，适应性对演化过程进行调整和分析^［9-10］.其二，以有限理性替代完全理性，考虑博弈主体会犯错以及多种因素的不确定性，更符合实际情况.因此，演化博弈论在经济管理等相关领域得到了广泛应用^［11-12］.为进一步剖析“监管困局”的内在形成机理并加以破解，一些学者采用演化博弈的方法建立了监管机制.如文献［13］构建了生产者、消费者和监管者构成的两期博弈模型，剖析食品安全“监管困局”的内在形成机理.文献［14］通过构建“平台卖家—平台电商—政府”的演化博弈模型，剖析平台电商信用“监管困局”的内在形成机理并加以破解.文献［15］构建“政府-平台-企业”3个主体之间的非对称演化博弈模型，通过数值仿真分析政府补贴力度和平台成本分担比例对系统演化稳定策略的影响.

已有的国内外相关文献为文中的研究提供较好的基础和研究参考，也为平台经济协同监管与激励机制的研究奠定了理论基础.尤其是数字经济治理、平台经济治理等相关热点问题的研究已经涉及了协同监管方面的内容，为做好平台经济多主体协同监管的研究提供了思路.但是，既有研究从内容看，缺乏对于平台经济多主体监管框架及激励机制的系统研究.国外对于平台经济多主体协同监管的研究大多集中在治理的意义、案例或困境方面，对于平台经济多主体协同监管研究的借鉴作用有限.国内对于平台经济多主体协同监管及激励机制的研究尚处于起步阶段，对于平台经济多主体协同监管的分析框架、监管主体识别、激励机制设计等方面，都还缺乏有价值的研究成果，无法为决策提供科学依据.

基于此，文中以政府、平台电商、平台卖家为研究对象，以演化博弈理论为基础，构建政府—平台电商—平台卖家的三方演化博弈模型，重点分析在信息不对称情况下，多主体协同监管对平台卖家行为选择策略的影响，通过案例数值仿真讨论了成本、惩罚力度等外生变量对各主体最优策略选择与期望收益的影响，冀期能够为数字经济背景下大数据“杀熟”监管激励的理论有所补充.因此，文中的主要贡献在于：首先，考虑到平台电商信用监管困局，引入政府规制，建立多元主体协同监管机制；其次，引入演化博弈理论，在有限理性的假设条件下分析政府、平台电商与平台卖家的决策策略、期望收益等，理清多元主体协同监管激励机制的内在机理；最后，通过数值仿真分析政府、平台电商、平台卖家达到最优稳定状态的均衡条件，实现监管激励下各方利益最大化的目标相容，进一步补充了大数据“杀熟”监管理论.

1 演化博弈模型构建

1.1 基本假设

（1） 博弈主体假设.文中演化博弈模型中涉及到的博弈主体有政府、平台电商和平台卖家：① 政府：在互联网背景下，政府制定处罚、税收、补贴等管理措施是促进网络平台市场公平定价、维护消费者权益的重要保障.在大数据“杀熟”协同监管过程中，政府可以制定管理措施，投入人力物力积极监管，或者采取放养式管理，不进行市场干预，消极监管.因此，政府的策略选择为｛积极监管，消极监管｝.② 平台电商：平台电商作为平台卖家的直接管理者，在完善优化网络定价方面有着举足轻重的地位.平台电商在平台交易中可以可持续发展为目标，承担监管主体责任积极监管，或者以利润最大化为原则消极监管.因此，平台电商的策略选择为｛积极监管，消极监管｝.③ 平台卖家：平台卖家是优化平台交易环境的中坚力量和主要实施者，在平台交易中可以选择诚信为本，公平定价，或者利益至上，选择“杀熟”定价.

（2） 设大数据“杀熟”监管过程中，政府选择积极监管的概率为x（0≤x≤1），则政府选择消极监管概率为1－x；平台电商选择积极监管的概率为y（0≤y≤1），则选择消极监管概率为1－y；平台卖家选择公平定价的概率为z（0≤z≤1），则杀熟定价的概率为1－z.

1.2 参数设置

3个博弈主体都可以通过不断学习、模仿来调整自身的策略行为选择，最终达到博弈均衡.模型相关假设及说明如表1.

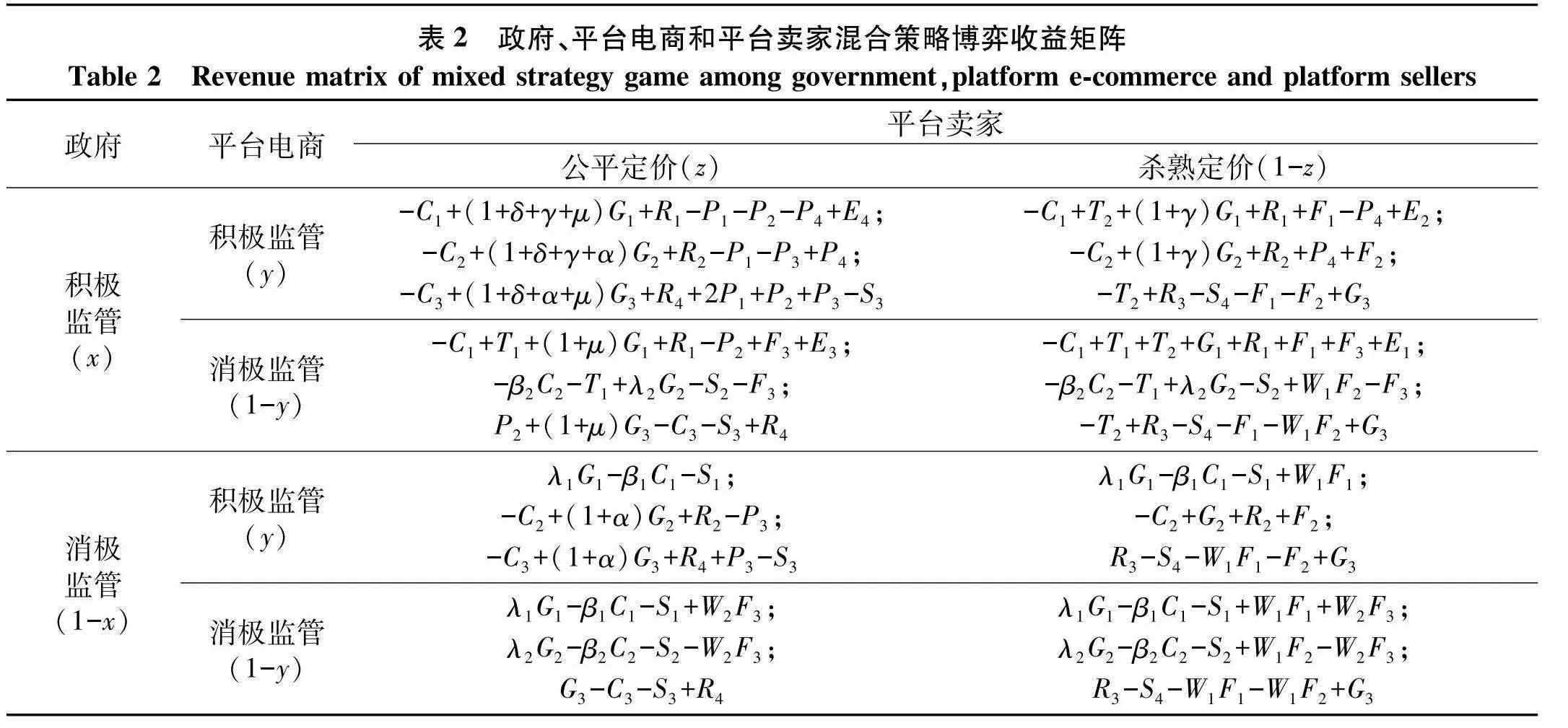
根据上述假设，可得三方演化博弈矩阵如表2.

2 演化稳定策略求解

2.1 三方复制动态方程分析

根据模型假设，令政府积极监管、不积极监管以及其平均收益分别为UI、UNI和UI，则有：

UI=yz×（δG1－P1+E4－E2－E3+E1）+y×（γG1－T1－F3-

P4+E2－E1）+z×（μG1－T2－F1－P2+ E3－E1）－

C1（μG1－T2－F1－P2+E3－E1）－C1+R1+T2+F1+T1+

F3+G1+E1

UNI=λ1G1－β1C1－S1+（1－z）W1F1+（1－y）W2F3

UI=x×UI+（1－x）×UNI

同理可得平台电商积极监管的期望收益UP、消极监管的期望收益UNP及其平均收益UP如下：

UP=xz×（δG2－P1）+x×（γG1+P4）+z×（αG2－F2－

P3）－C2+R2+F2+G2

UNP=x（－T1－F3+W2F3）－zW1F2－β2C2+λ2G2－S2+

W1F2－W2F3

UP=y×UP+（1－y）×UNP

则平台卖家公平定价的期望收益UC、杀熟定价的期望收益UNC及平均收益UC为：

UC=xy×（δG3+2P1）+x×（μG3+P2）+y×（αG3+P3）-

C3－S3+R4+G3

UNC=x（－T2－F1+W1F1）+y（－F2+W1F2）+R3－S4－

W1F1－W1F2+G3

UC=z×UC+（1－z）×UNC

复制动态微分方程的基本原理，即参与者选取某种策略的增长率dθ（t）/dt与该时期t选取该策略的人数比例成正比，而且与选取该策略的收益与平均收益的差值成正比.据此，则政府、平台电商和平台卖家的动态复制方程F（x），F（y），F（z）分别为：

F（x）=dxdt=x×（UI－UI）=x×（1－x）×（UI－UNI）=

x×（1－x）×［yz×（δG1－P1+E4－E2－E3+E1）+

y×（γG1－T1－F3－P4+W2F3+E2－E1）+

z×（μG1－T2－F1－P2+W1F1+E3－E1）+E1+

（β1－1）C1+（1－λ1）G1+R1+T2+F1+T1+F3+

S1－W1F1－W2F3］

F（y）=dydt=y×（UP－UP）=

y×（1－y）×（UP－UNP）=

y×（1－y）×［xz×（δG2－P1）+x×（γG2+T1+

F3+P4－W2F3）+z×（αG2－P3－F2+W1F2）+

（β2－1）C2+（1－λ2）G2+R2+F2+S2－W1F2+

W2F3］

F（z）=dzdt=z×（UC－UC）=z×（1－z）×（UC－UNC）=

z×（1－z）×［yx×（δG3+2P1）+x×（μG3+

P2+T2+F1－W1F1）+y×（αG3+P3+F2－

W1F2）－C3－S3－R3+R4+S4+W1F1+W1F2］

2.2 三方演化路径及其稳定性分析

采用微分方程稳定性定理来分析3个博弈主体的稳定性和策略演化路径.根据微分方程的稳定性定理，政府、平台和电商的复制动态方程的稳定点应满足如下条件：

F（x）=0，F（x）xlt;0；

F（y）=0，F（y）ylt;0；

F（z）=0，F（z）zlt;0，其中

F（x）x=（1－2x）×［yz×（δG1－P1+E4－E2－E3+E1）+y×

（γG1－T1－F3－P4+W2F3+E2－E1）+z×（μG1－T2－F1－

P2+W1F1+E3－E1）+E1+（β1－1）C1+（1－λ1）G1+R1+

T2+F1+T1+F3+S1－W1F1－W2F3］；

F（y）y=（1－2y）×［xz×（δG2－P1）+x×（γG2+T1+ F3+

P4－W2F3）+z×（αG2－P3－F2+W1F2）+（β2－1）C2+

（1－λ2）G2+R2+F2+S2－W1F2+W2F3］；

F（z）z=（1－2z）×［yx×（δG3+2P1）+x×（μG3+P2+T2+F1－W1F1）+

y×（αG3+P3+F2－W1F2）－C3－S3－R3+R4+S4+W1F1+W1F2］

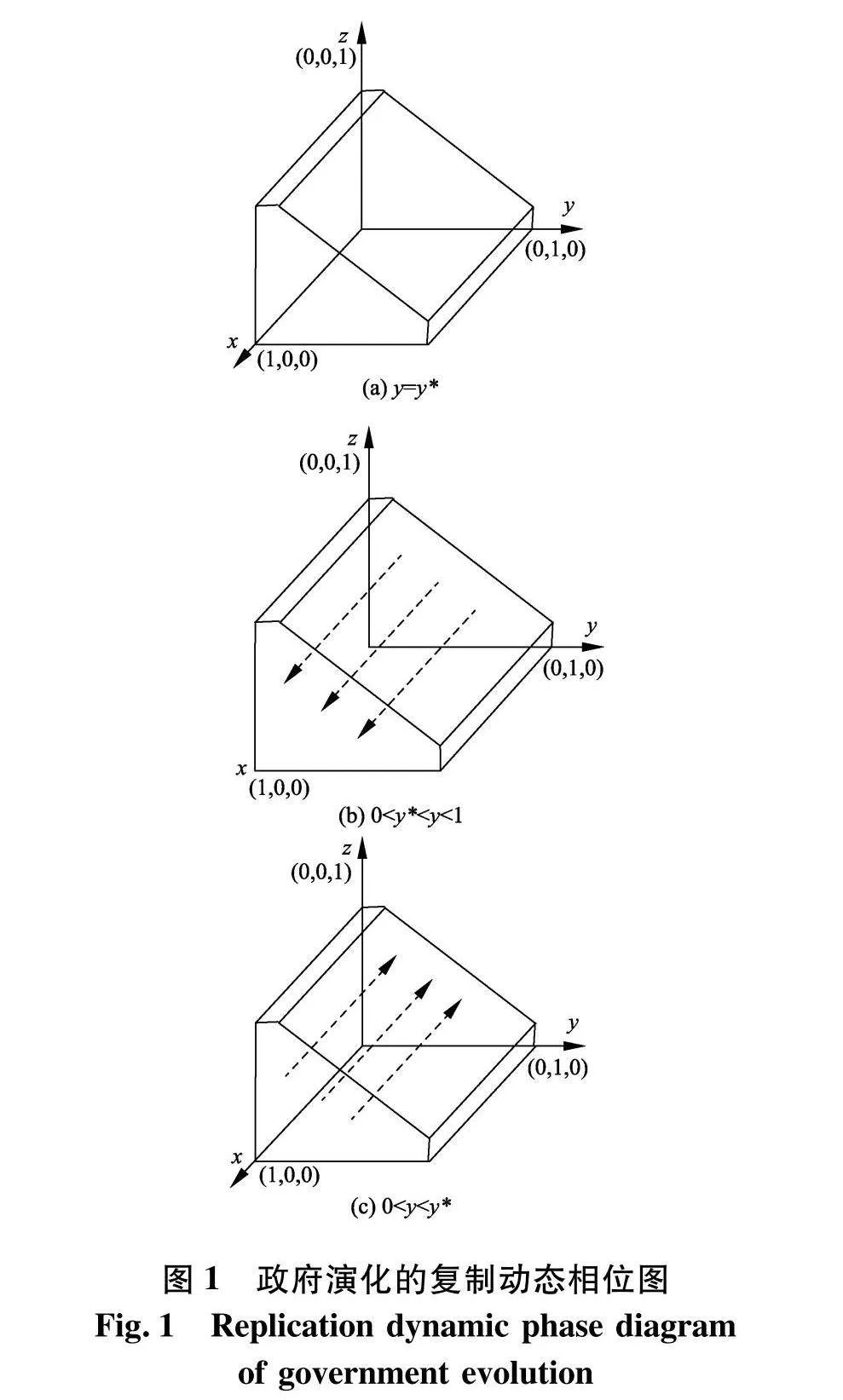
进一步可得出政府演化的动态复制相位如图1（令y*=（1－β1）C1+（λ1－1）G1－E1－R1－T2－F1－T1－F3－S1+W1F1+W2F3－z×（μG1－T2－F1－P2+W1F1+E3－E1）z×（δG1－P1+E4－E2－E3+E1）+γG1－T1－F3－P4+W2F3+E2－E1）.

从图1中可知，政府的演化策略的走向既受到模型中各参数的影响，也受平台电商和平台卖家策略选择的影响.当0lt;ylt;y*时，政府的稳定策略为“消极监管”；当0lt;y*lt;ylt;1时，政府的稳定策略为“积极监管”；当y=y*时，政府的任何策略都为稳定状态.

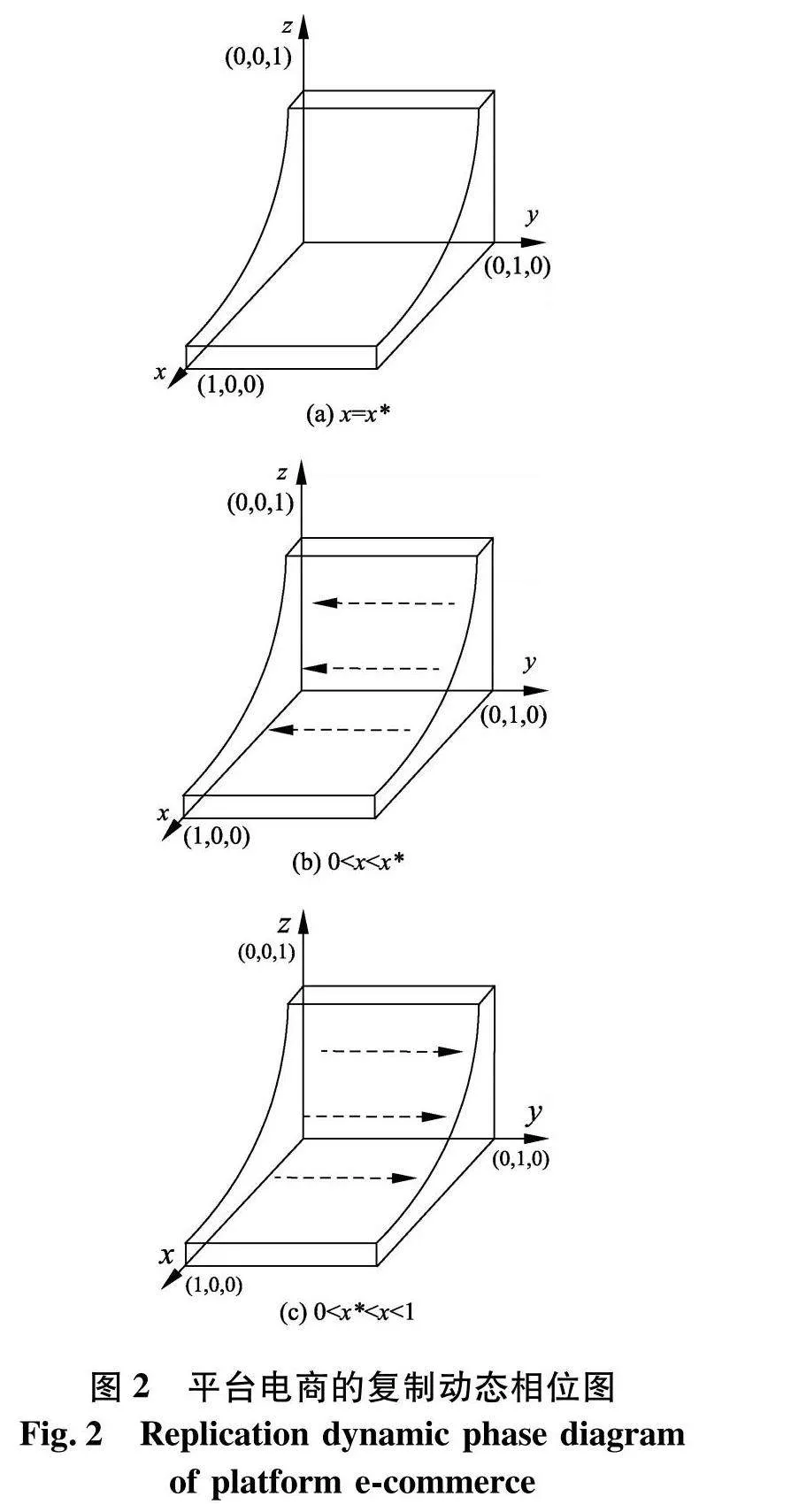
类似的，得出平台电商的复制动态相位图如图2（令x*=（1－β2）C2+（λ2－1）G2－R2－F2－S2+W1F2－W2F3－z*（αG2－P3－F2+W1F2）z×（δG2－P1）+γG2+T1+F3+P4－W2F3）.

从图2中可知，平台电商的演化策略的走向既受到模型中各参数的影响，也受政府和平台卖家的策略选择的影响.当0lt;x*lt;xlt;1时，平台电商的稳定策略为“积极监管”；当 0lt;xlt;x*时，平台电商的稳定策略为“消极监管”；当x=x*时，平台电商的任何策略都为稳定状态.

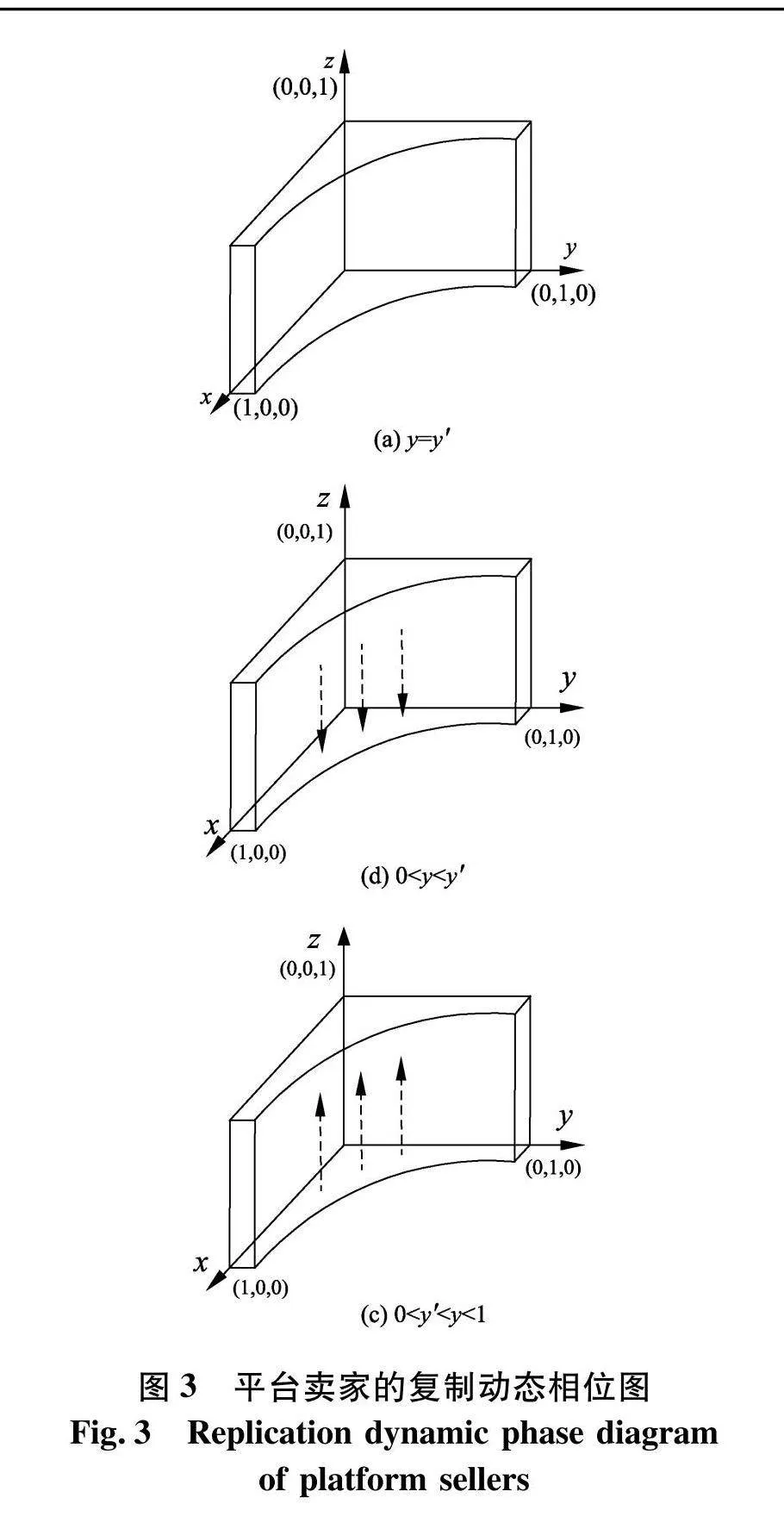
同理，平台卖家的复制动态相位图如图3（令y′=C3+S3+R3－R4－S4－W1F1－W1F2－x×（μG3+P2+T2+F1－W1F1）x×（δG3+2P1）+αG3+P3+F2－W1F2）.

从图3中可知，平台卖家的演化策略的走向既受到模型中各参数的影响，也受平台电商的影响.当0lt;y′lt;ylt;1时，平台卖家的稳定策略为“公平定价”；当0lt;ylt;y′时，平台卖家的稳定策略为“杀熟定价”；当y=y′时，平台卖家的任何策略都为稳定状态.

2.3 三方共同作用的演化策略稳定性分析

上一小节从单个博弈主体的行为选择出发，分析了各主体策略演化过程及其行为影响因素，但平台经济的稳定健康发展需要政府、平台电商和平台卖家的共同作用，因此统筹研究具有重大意义.根据Ritzberger（1996），三方演化博弈策略，只需要分析E1（0，0，0）、E2（1，0，0）、E3（0，1，0）、E4（0，0，1）、E5（1，1，0）、E6（1，0，1）、E7（0，1，1）、E8（1，1，1）的渐进稳定性.根据Fridman（1991）提出的方法，对于一个由微分方程系统描述的群体动态，其均衡点的稳定性是由该系统的雅可比矩阵分析得到的.基于前文所述的复制动态方程，可以得出雅克比矩阵：

J=J11J12J13J21J22J23J31J32J33，其中，各单元具体数值如下：

J11=（1－2x）×［yz×（δG1－P1+E4－E2－E3+E1）+

y×（γG1－T1－F3－P4+W2F3+E2－E1）+

z×（μG1－T2－F1－P2+W1F1+E3－E1）+E1+

（β1－1）C1+ （1－λ1）G1+R1+T2+F1+T1+F3+

S1－W1F1－W2F3］

J12=x×（1－x）×［z×（δG1－P1+E4－E2－E3+E1）+

γG1－T1－F3－P4+W2F3+E2－E1］

J13=x×（1－x）×［y（δG1－P1+E4－E2－E3+E1）+

μG1－P2－T2－F1+W1F1+E3－E1］

J21=y×（1－y）×（z×（δG2－P1）+γG2+T1+F3+P4－W2F3）

J22=（1－2y）×［xz×（δG2－P1）+x×（γG2+T1+F3+P4－W2F3）+

z×（αG2－P3－F2+W1F2）+（β2－1）C2+（1－λ2）G2+R2+

F2+S2－W1F2+W2F3］

J23=y×（1－y）×［x×（δG2－P1）+αG2－P3－F2+W1F2）

J31=z×（1－z）［y×（δG3+2P1）+μG3+P2+T2+F1－W1F1］

J32=z×（1－z）×［x×（δG3+2P1）+αG3+P3+F2－W1F2］

J33=（1－2z）×［yx×（δG3+2P1）+x×（μG3+P2+T2+F1－W1F1）+

y×（αG3+P3+F2－W1F2）－C3－S3+R4－R3+S4+

W1F1+W1F2］

若均衡点满足detJgt;0，trJlt;0两个条件，则均衡点为演化动态过程的局部渐近稳定点.根据雅可比矩阵的局部稳定分析法，结果如表3.

文中主要分析达到政府积极监管、平台积极监管、电商公平定价的稳定状态，即分析E8（1，1，1）的现实约束，在表3的基础上，可知，若满足：

（1） －δG1+P1－E4－γG1+T1+F3+P4－W2F3－μG1+T2+F1+P2－W1F1+（1－β1）C1+（λ1－1）G1－R1－T2－F1－T1－F3－S1+W1F1+W2F3lt;0，

（2） －δG2+P1－γG2－T1－F3－P4+W2F3－αG2+P3+F2－W1F2+（1－β2）C2+（λ2－1）G2－R2－F2－S2+W1F2－W2F3lt;0，

（3） －δG3－2P1－μG3－P2－T2－F1+W1F1－αG3－P3－F2+W1F2+C3+S3－R4+R3－S4－W1F1－W1F2lt;0，

此时，E8为均衡点.

3 仿真演化博弈

在政府、平台电商与平台卖家构建的动力系统中，涉及不同策略组合的收益与成本，采取不同组合策略的概率分布等参数或变量，都可以通过雅可比矩阵判断演化系统在平衡点的稳定性，但是难以详细刻画均衡的实现过程以及不同参数对演化过程的影响.为了在不同情形下对政府、平台电商与平台卖家之间的演化博弈过程进行分析，本文采用数值分析的方法对理论分析进行验证，即通过对模型参数进行取值，模拟政府、平台电商与平台卖家之间博弈的变动趋势，进而系统全面的揭示政府、平台电商与平台卖家进行决策的一般性规律.

文中数值分析参数以著名网络平台电商某宝旗下商城的一桩“杀熟”事件为例，2020年3月7日，某宝用户称会员在其商城购买商品时价格比普通用户更高，随后更多网友发现该商城存在严重的“杀熟”定价行为，比如，3.8妇女节活动期间，一款洗面奶在不同用户、不同型号手机上有至少5种不同的价格，由低到高一次为16.03，21.9，24.9，31.7，35.46元.即使是同一个用户，使用不同帐号登录，显示的价格亦不同.此类现象在该平台并不限于上述化妆品一案，有网友计算出，该商城针对不同用户的价格差别约为10%.事实上，对于“大数据杀熟”，《中华人民共和国价格法》明确规定，经营者不得对提供相同商品或者服务，对具有同等交易条件的其他经营者实行价格歧视.违反该规定的，责令改正，没收违法所得，并处违法所得5倍以下的罚款.

以上述案例为背景，文中特设在政府、平台电商与平台卖家的博弈系统中，政府介入监管需付出成本50万元，平台监管花费48万元，卖家公平定价付出成本40万元，地方政府积极监管会获得额外收益5万元，同时会获得中央政府基本奖励10万元，政府不积极监管造成的名誉等损失5万元，同时损失基本收益比率0.8，若平台积极监管，会获得额外收益及政府相关补贴5万元，平台若不积极监管，也会被政府处以3万元的罚款，平台卖家若杀熟定价，会获得额外收益7万元，造成客户流失等损失4万元，违规行为若被发现没收违法所得9万元，若公平定价，短期内造成利润损失7万元.

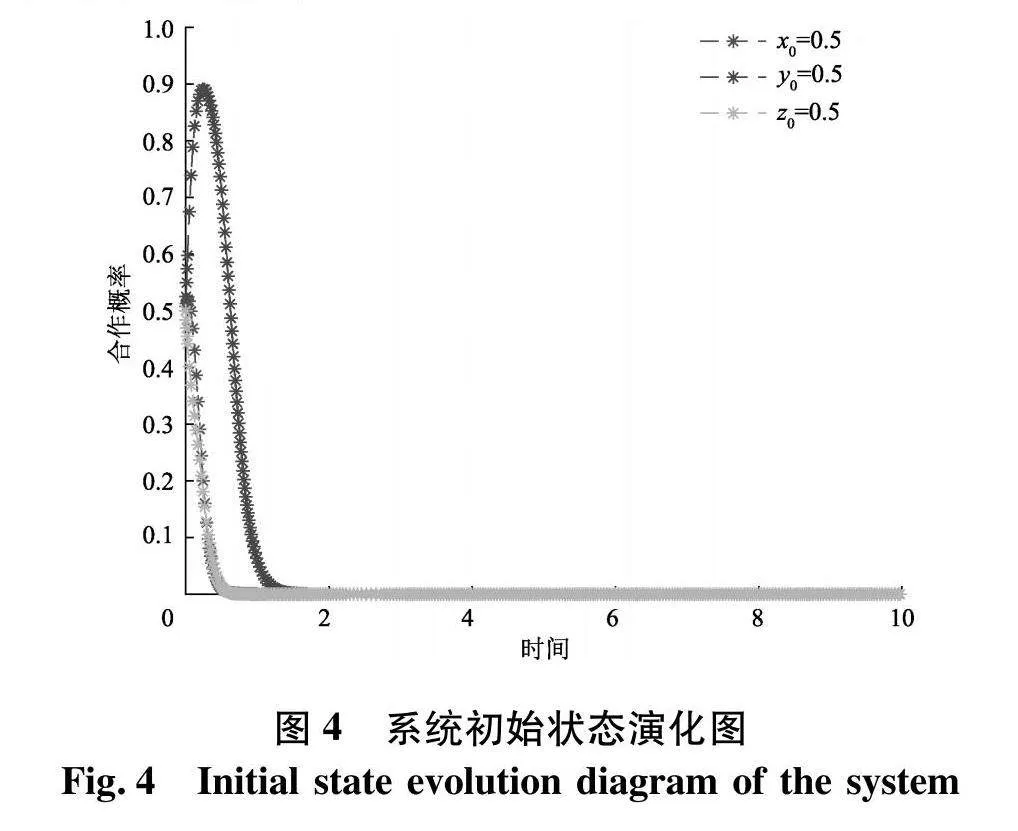
综上，本节利用Matlab软件做仿真分析，分别探讨在不同参数影响下博弈双方的演化结果.初始结果如图4.其中，x0为政府选择积极监管策略的初始概率，y0为平台电商采取积极监管的初始概率，z0为平台卖家公平定价的初始概率，横坐标表示演化博弈的时间，纵坐标表示各主体行为选择的概率.因初始演化强调自然状态下各方的选择结果，特设三方主体的初始概率为0.5，演化结果如图4，表明系统自发的演化稳定趋于（0，0，0），即政府选择消极监管，平台电商选择消极监管，平台卖家趋于“杀熟”定价.

3.1 成本对系统演化的影响

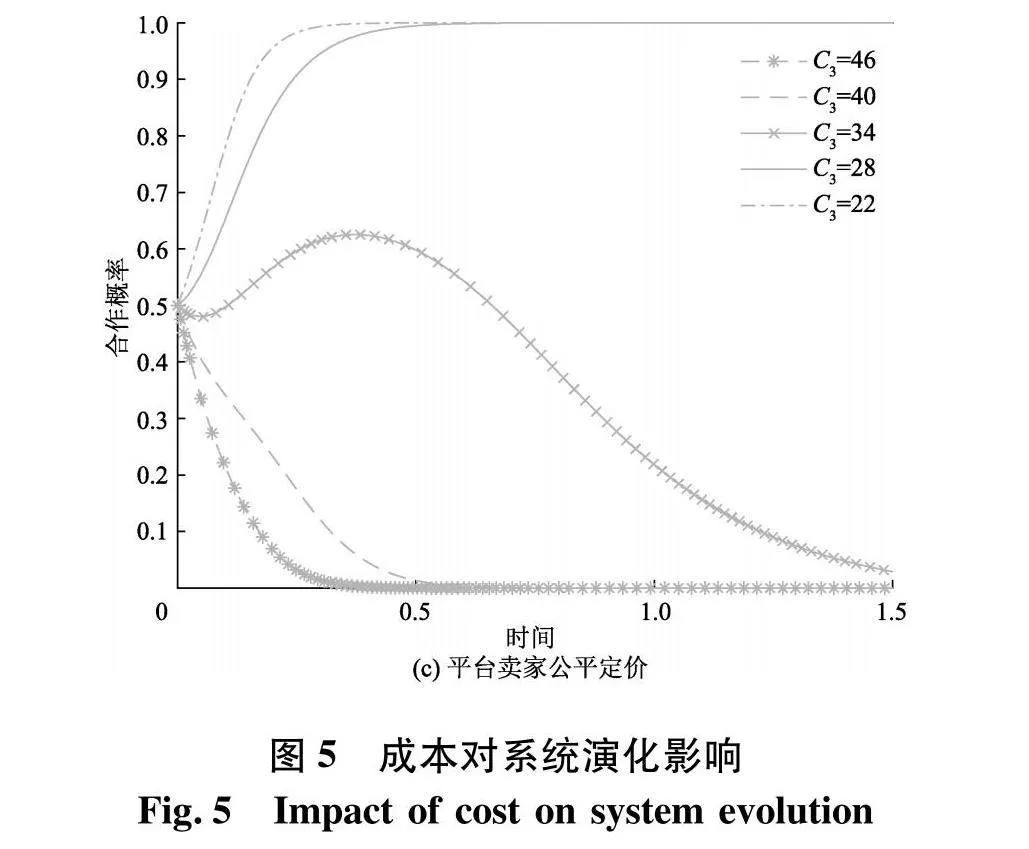
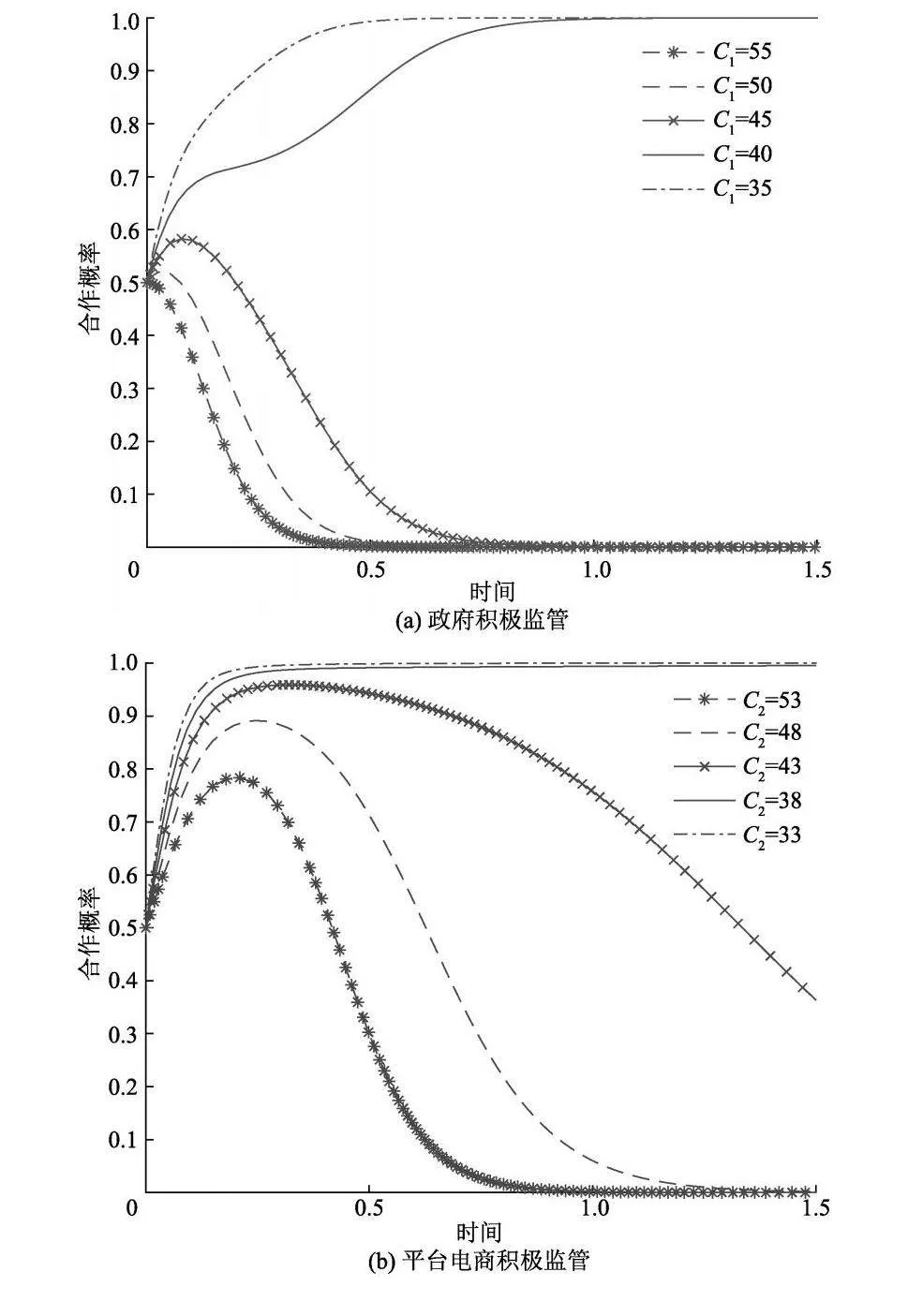
为验证成本对各主体行为选择的影响，分别取政府积极监管成本为55、50、45、40、35，平台电商积极监管成本为53、48、43、38、33，平台卖家公平定价花费的成本为46、40、34、28、22.演化结果如图5.

研究结果表明，成本对于系统演化稳定具有决定性影响.对于政府而言，总体上政府采取积极监管的概率随着监管成本的减小而增大.具体来说，以演化时间1为界，当政府监管成本为55和50时，政府在1处均已达到消极监管的稳定状态，且成本越大，政府会以更快的速度选择消极监管.政府在网络市场监管过程中，因信息不对称问题以及卖家投机行为的隐蔽性特点，监管本身存在较大难度，往往无法达到预期标准.此时，若监管成本很高，政府高成本投入并不能切实纠察平台交易违规行为，便更倾向消极监管.当监管成本的降低到45时，政府在演化初期以大于0.5的概率倾向选择积极监管，但随着时间推移，政府最终还是选择消极监管并保持稳定.当监管成本降到45以下时，政府财政压力减小，为切实履行社会责任，树立政府形象，打造良好的社会公信力，政府会以较快的速度选择积极监管.

同样，平台电商积极监管的概率随着成本的降低而增大.当监管成本较高时，平台电商与平台卖家缔结的组织内委托代理关系使得平台电商更倾向舍弃高额成本支出进行监管，转而维护平台卖家以获取更多利润.而当监管成本降到一定程度，平台电商以较小的支出，便能收获顾客信任、声誉等社会效益，符合可持续发展的经营理念，由此，平台电商会快速转向积极监管，并且成本越低，速率越快.

作为以盈利性为目的的经济组织，平台卖家更是“利益优先”，以利益最大化作为其行为选择的重要依据，因此平台卖家对成本变化的敏感性要高于平台电商与政府.平台卖家选择公平定价时，相对于“杀熟定价”本身会损失一部分额外收益，因此成本较高时，平台卖家会毫不犹豫选择“杀熟定价”，而且成本越高，速率越快.定价成本较低时，平台卖家若选择公平定价，便能以较低的支出收获口碑、消费者忠诚等社会效益，同时，还能收获政府与平台电商的相关补贴，一定程度上弥补了公平定价的损失，因此，平台卖家会积极选择公平定价.

3.2 惩罚对系统演化的影响

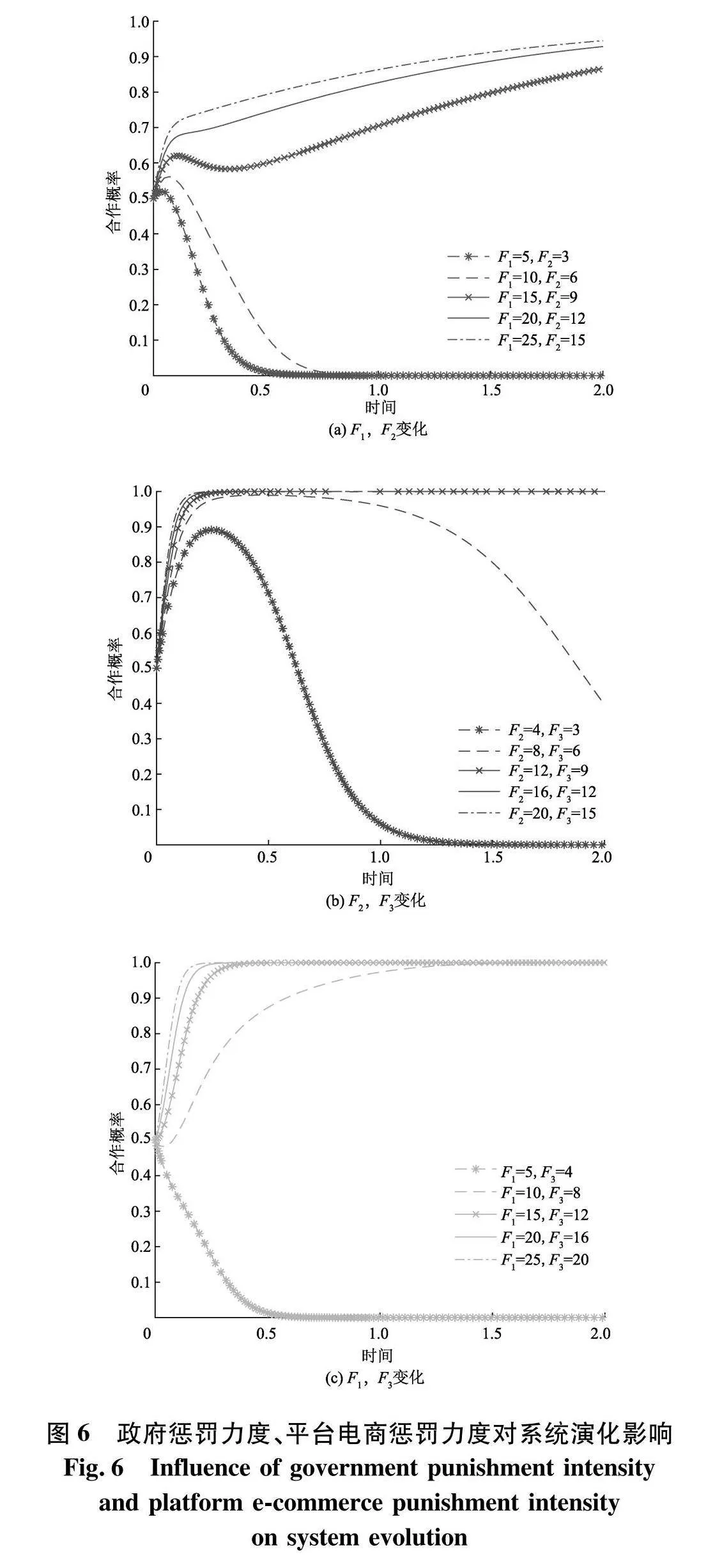
探究各监管主体的惩罚措施对于系统演化的影响，仿真结果如图6.

研究结果表明，惩罚对于系统演化稳定具有重要作用.惩罚措施对于各监管主体属于非正式收入.尤其政府作为主要监管主体，其惩罚力度更能反应出政府对整治平台乱象的重视程度，惩罚力度越高，政府越倾向于选择积极监管.对于平台电商而言，一方面承受政府对其消极监管的惩罚支出，一方面收获监管平台卖家违规行为带来的惩罚收入.随着政府惩罚力度的增强，平台消极监管带来的损失增加，当损失增强到一定程度，平台会降低违规行为发生的概率，同时增强对平台卖家的监管，以期通过对平台卖家投机行为的惩罚获取相应的收入补贴，由此，平台会逐渐转向积极监管.同时，由图可知，当惩罚支出与惩罚收入差距较小时，平台电商倾向选择消极监管.随着各监管主体惩罚力度的增加，当惩罚收入远高于惩罚支出时，平台会选择积极监管.平台卖家作为惩罚措施的实施对象，当政府与平台电商惩罚力度较小时，对平台卖家造成的损失不足以抵消“杀熟定价”获得的额外收益，平台卖家仍会坚持“杀熟定价”.随着各监管主体惩罚力度的增强，平台卖家若继续开展违规行为便面临着高额损失，由此，卖家会在较短时间内选择公平定价，减少“杀熟定价”带来的亏损.

3.3 监管力度对系统演化的影响

（1） 政府监管力度对系统演化的影响

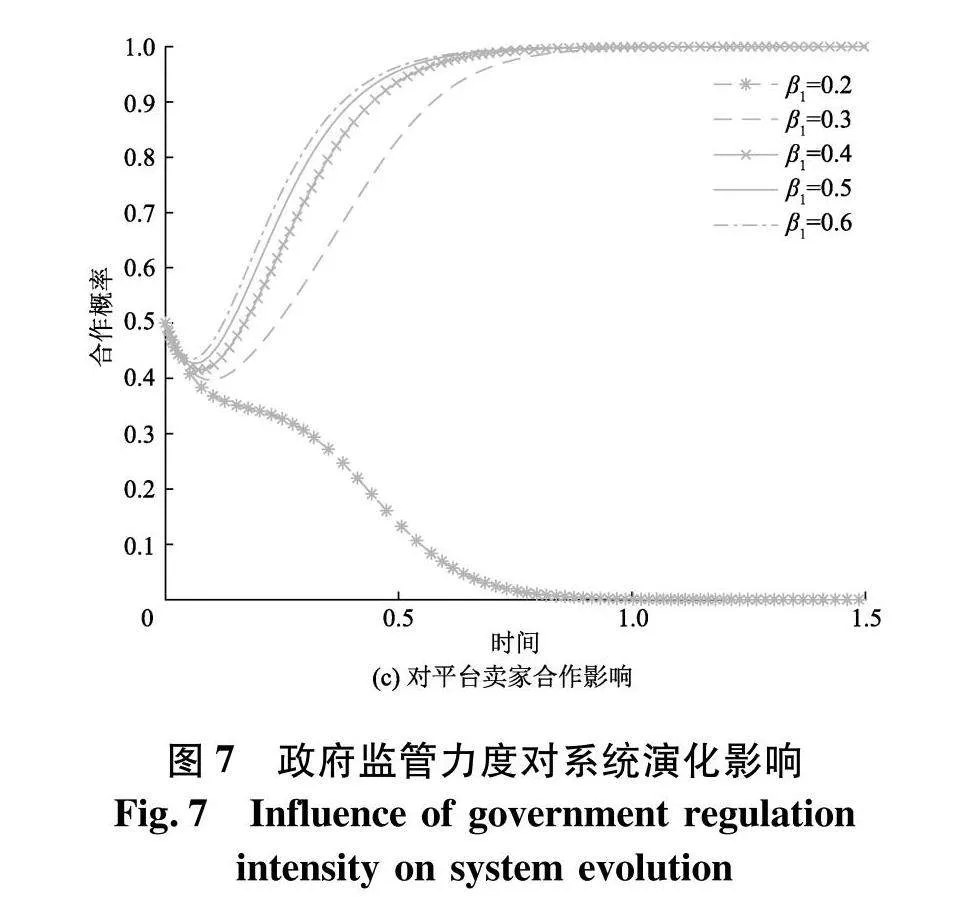
为探究政府监管力度对系统演化的影响，对政府监管力度系数分别取0.2，0.3，0.4，0.5，0.6，仿真结果如图7.

由图7可知，随着政府监管力度的增强，系统最终达到（积极监管，积极监管，公平定价）的理想状态，并且保持长期稳定.具体来说，以演化时间0.5为界，当政府监管系数为0.2时，政府倾向选择消极监管，而平台电商与平台卖家则均在0.5之前分别达到消极监管与杀熟定价的状态.表明当政府监管力度较小时，政府会花费较少的人力物力改造平台监管机制、降低对违规行为的惩治力度，但因信息不对称性以及卖家投机行为的隐蔽性特点，较小的监管力度无法切实优化网络市场环境，久之政府便开始消极监管.而平台电商与平台卖家在缺少政府管控情况下，更是以自身利益最大化为原则，继续保持投机行为.当政府监管力度上升到0.3时，仍以演化时间0.5为界，政府以高于0.9的概率倾向于积极监管并保持稳定，平台电商有选择消极监管的倾向，但因政府监管力度的增强，最终迫于政府压力转而选择积极监管，并保持稳定.而平台卖家在0.5时已经达到杀熟定价的状态，作为盈利性组织，其第一选择就是能获得额外收益的“杀熟定价”，但政府的强力监管会增加平台卖家被曝光的风险，不仅面临高额惩罚支出，还会影响卖家声誉、降低顾客忠诚度，不利于卖家的可持续发展，为维持企业形象，考虑企业的长期发展，卖家最终会选择公平定价.随着监管力度增强到0.3以上，政府、平台电商与平台卖家均会以较快的速度达到（积极监管，积极监管，公平定价）的稳定状态，并且监管力度越大，达到稳定状态的速率越快.基于此，政府可以通过加强监管力度，提高罚金、增加监督检查频率等措施，增加平台电商与平台卖家的违规损失，促进平台电商、平台卖家规范行为的形成.

（2） 平台电商监管力度对系统演化的影响

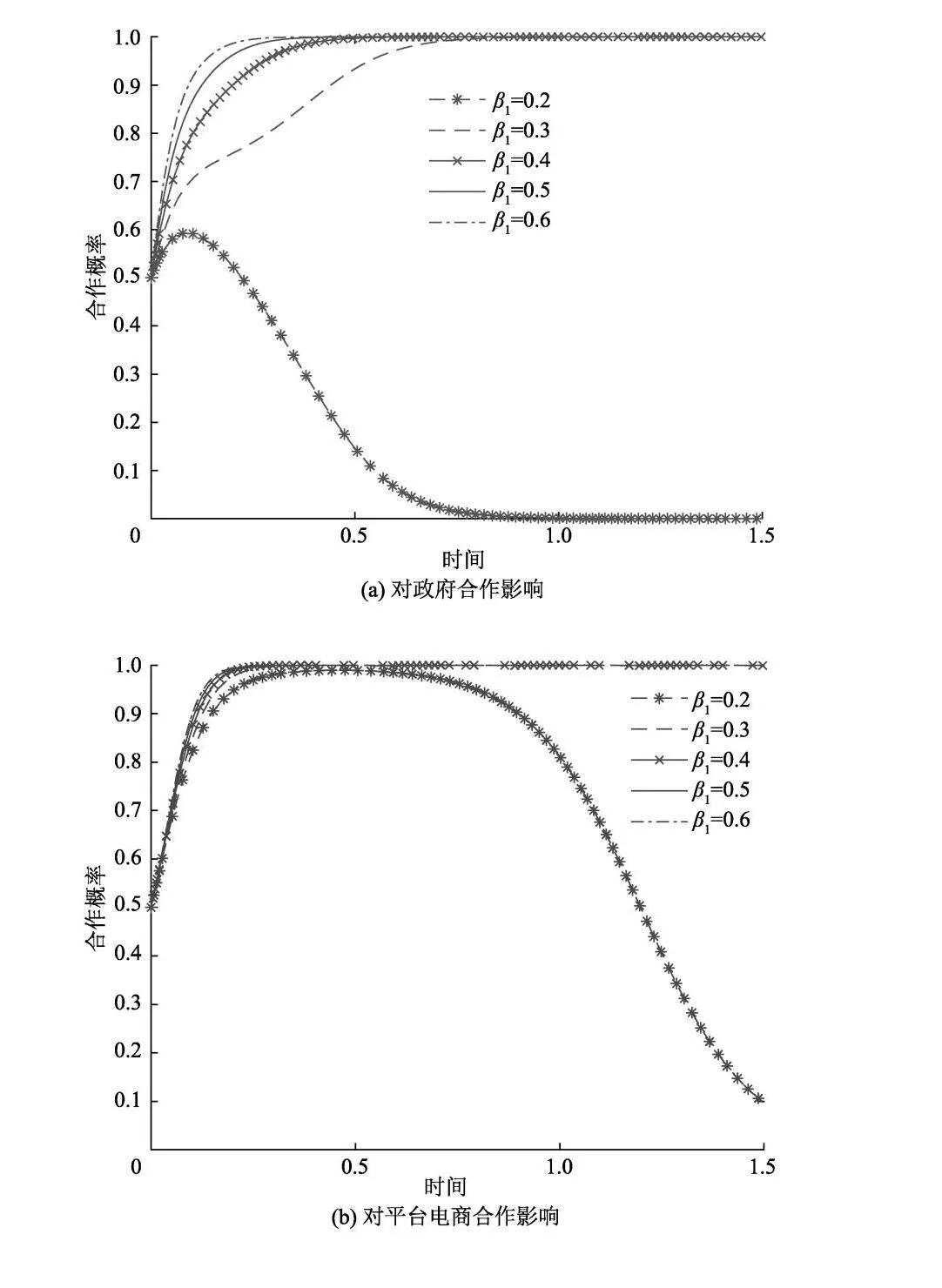
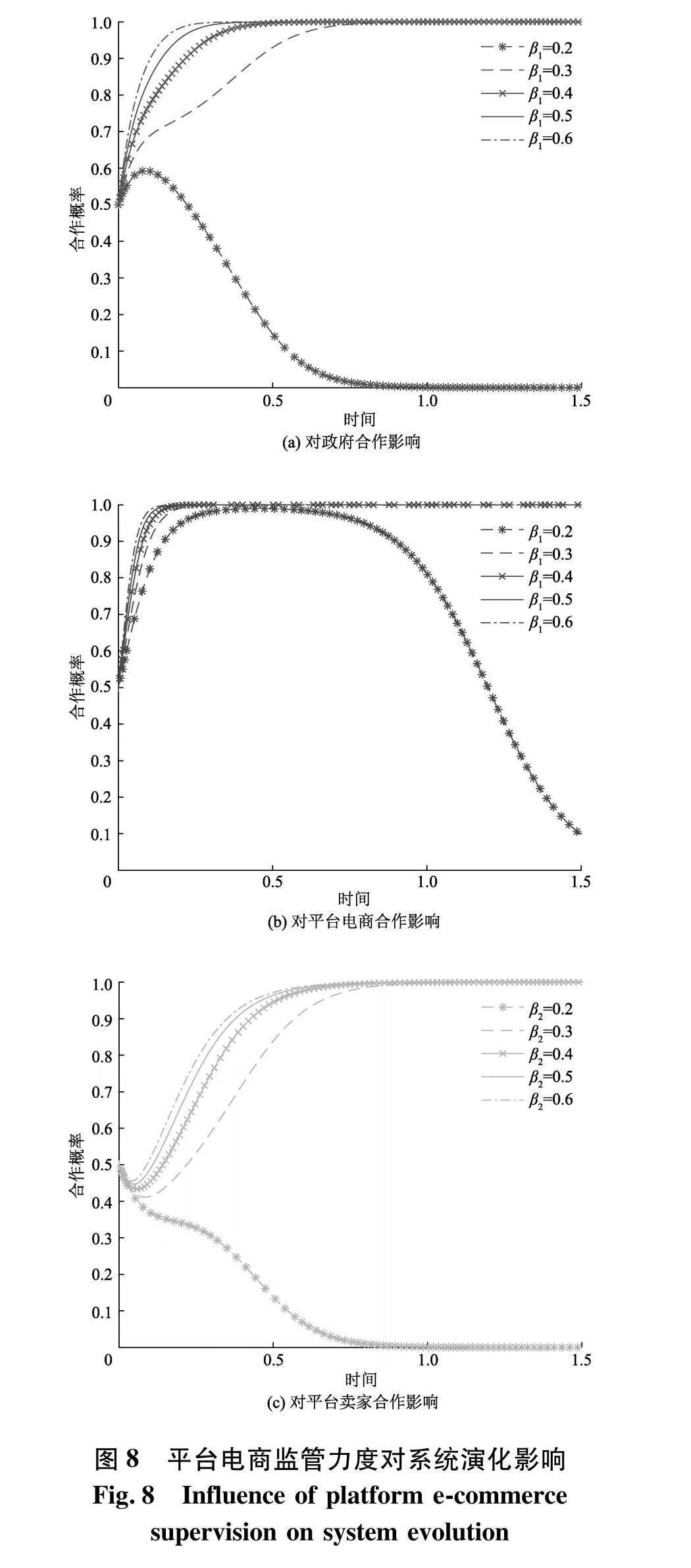
为探究平台电商监管力度对系统演化的影响，分别取平台监管系数为0.2，0.3，0.4，0.5，0.6，数值仿真分析结果如图8.

由图8可知，平台监管力度增强，有利于系统达到（积极监管，积极监管，公平定价）的稳定状态.具体来说，以演化时间0.5为界，当平台监管系数为0.2，0.3，0.4时，政府选择消极监管，而平台电商与平台卖家则分别选择消极监管与杀熟定价.可见，当平台电商监管力度较小时，不足以遏制平台卖家通过投机行为攫取高额利润，因此平台卖家会选择杀熟定价.平台电商的监管投入不仅无法遏制平台乱象，还要持续投入支出，以自身利益为着眼点，平台电商最终会选择消极监管.对于政府而言，平台监管力度并未对政府产生影响，政府会保持其初始选择消极监管.而当平台监管力度大于0.4时，系统最终会达到（积极监管，积极监管，公平定价）的理想状态并保持稳定，且监管力度越大，达到理想稳定状态的速率越快.具体来说，当平台电商监管力度足够大，平台卖家投机行为带来的收益不足以弥补平台电商高强度监管带来的损失，平台卖家便会减少投机行为，转向选择公平定价.对于平台电商，其监管力度越大，获得的财政收益与社会效益越大，平台电商就越会选择积极监管.此时，通过平台电商的监管，已经在很大程度上遏制了卖家的投机行为，降低了政府监管网络交易市场的难度，为维护政府形象，获取民众信任、声誉等社会效益，政府会主动承担监管责任积极监管，并且随着平台电商监管力度的增强，达到稳定状态的速率越快.可见，平台电商亦可通过加强监管力度，带动各主体达到理想的稳定状态.

此外，通过对比图7，8还可以看出，政府监管力度能对各主体行为产生显著影响，而平台监管力度需要达到一定程度才会影响系统状态，但平台监管相较政府监管能在更短时间内促使各主体达到稳定状态.进一步说明了政府与平台电商协同监管的必要性，能保证监管主体以最小的人力物力快速达到稳定状态.

（3） 政府与平台电商协同监管对系统演化的影响

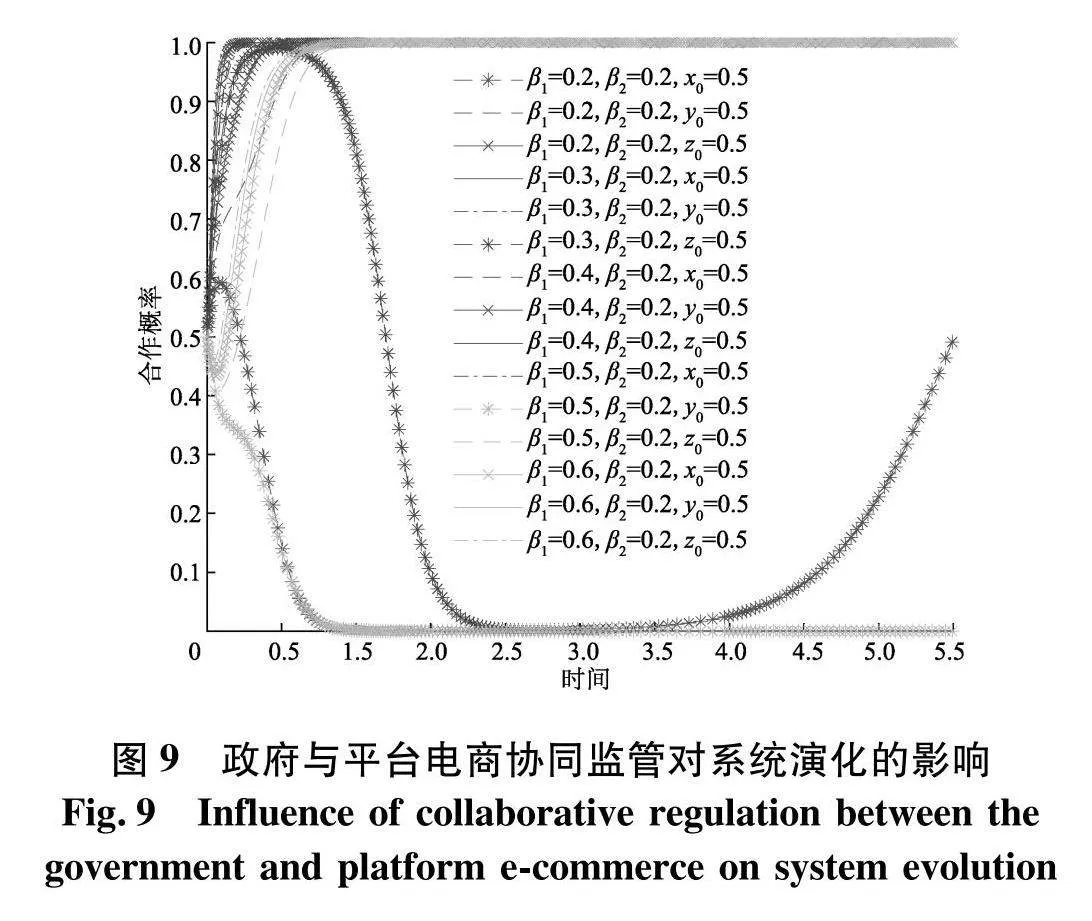
上述结论可见协同监管的必要性，为进一步探究政府与平台电商协同监管作用下系统的演化规律，将两主体监管力度合并实施，仿真结果如图9.

由图9可知，即使政府与平台电商都保持较低力度的监管水平，也会促使整个系统在短时间内向（积极监管，积极监管，公平定价）的方向演化并且保持稳定.这也就意味着政府与平台电商协同监管的效果优于政府或者平台电商单独监管的作用，加强政府与平台电商的有效互动是必要的.

4 结论与对策建议

根据以上分析，文中得出主要结论：① 在自然状态下，政府、平台电商与平台卖家构建的博弈模型很难向着（积极监管，积极监管，公平定价）的理想状态自然演化.② 成本、惩罚力度、政府与平台电商的监管力度等参数对系统达到理想状态具有重要意义.③ 政府与平台电商协同监管效果更具优越性，加强政府与平台电商的良性互动能以最小的支出换取最大化的收益.在此基础上，为能更好地发挥监管主体作用，打造更公平透明的市场交易环境，保护消费者权益，减少大数据环境下平台电商的“杀熟”行为，文中提出如下政策建议：

（1） 建立完善的法律规制体系，严惩重罚，绝不姑息

大数据“杀熟”行为涉及面比较广，需要多主体共同参与监管，其中，政府的监管监察具有不可替代的作用.对此，政府需将大数据“杀熟”行为纳入明确的法律治理范围内.对违规企业根据其具体情况施以严惩重罚，要触及违规卖家的“痛点”，增加其违法成本，使其不敢“再犯”.此外，可以规定网络平台应当公示其平台服务协议及支付规则，充分发挥政府监管的力量，真正刹住这种“薅用户羊毛”的失信行为，重构平台市场诚信交易的氛围.

（2） 增强各监管主体间的良性互动，增强监管力度，降低监管成本

政府要主动进行监管，加大监管力度，增强与平台电商间的良性互动，建立科学有效的信息共享渠道.提高对监管的资金投入，摒弃传统的监管方式，充分运用互联网、大数据等技术开展价格检测.

（3） 加大宣传，提高公众维权意识，发挥社会监督力量

多种监管方式并存可以形成实现多元共治.公众监督是对政府监督的一种有效补充，基于此，政府应充分利用新媒体平台的宣传优势，加强消费者维权知识的宣传教育工作，提高公众维权意识，降低举报成本.同时，对商家展开培训、教育，使其梳理正确的经营理念，自觉杜绝价格欺诈行为.

参考文献（References）

［1］ 汪旭晖，任晓雪. 政府治理视角下平台电商信用监管的动态演化博弈研究［J］.中国管理科学，2021，29（12）： 29-41.

［2］ LIN T，CHENG H K，WANG F S，et al. A study of online auction sellers′ intention to switch platform： The case of Yahoo！ Kimo versus Ruten_eBay［J］. Decision Sciences，2012，43（2）： 241-272.

［3］ GREWAL R，CHAKRAVARTY A， SAINI A. Governance mechanisms in Business-to-Business electronic markets ［J］. Journal of Marketing，2010，74（3）： 46-62.

［4］ PLAMBECK E L，TAYLOR T A. Supplier evasion of a buyer′s audit： Implications for motivating supplier social and environmental responsibility［J］. Manufacturing and Service Operations Management，2016，18（2）： 184-197.

［5］ 曹裕，俞传艳，万光羽. 政府参与下食品企业监管博弈研究［J］. 系统工程理论与实践，2017，37（1）： 140-150.

［6］ 赵荧梅，郭本海，刘思峰. 不完全信息下产品质量监管多方博弈模型［J］.中国管理科学，2017，25（2）： 111-120.

［7］ 朱立龙，郭鹏菲. 政府—冷链食品企业质量安全监管博弈分析［J］.中国管理科学，2016，24（增1） ：644-649.

［8］ EID M S，EL-ADAWAY I H，COATNEY K T. Evolutionary stable strategy for postdisaster insurance： Game theory approach［J］. Journal of Management in Engineering，2015，31（6）： 04015005.

［9］ 全吉，储育青，王先甲. 具有惩罚策略的公共物品博弈与合作演化［J］.系统工程理论与实践，2019，39（1）：141-149.

［10］ 王先甲，夏可. 多人雪堆演化博弈在愿景驱动规则下的扩展平均丰度函数［J］.系统工程理论与实践，2019，39（5）： 1128-1136.

［11］ CAI G S，KOCK N. An evolutionary game theoretic perspective on e-collaboration： The collaboration effort and media relativeness［J］. European Journal of Operational Research，2008，194（3）：821-833.

［12］ 杨丰梅，王安瑛，吴军，等. 基于博弈论的C2B2C模式下电商信用监管机制研究［J］.系统工程理论与实践，2017，37（8）： 2102-2110.

［13］ 谢康，肖静华，赖金天，等. 食品安全“监管困局”、信号扭曲与制度安排［J］.管理科学学报，2017，20（2）：1-17.

［14］ 汪旭晖，任晓雪. 基于演化博弈的平台电商信用监管机制研究［J］.系统工程理论与实践，2020，40（10）：2617-2630.

［15］ 周晓阳，赵凡，刘莹，等. 政府补贴和成本共担如何影响平台和企业策略选择—基于三方演化博弈［J］.控制与决策策，2022，37（2）： 293-302.

（责任编辑：顾琳）