基于BP神经网络的兰州新区现代有轨电车适用性评价
2024-01-11柴海华
柴海华
摘 要:在综合考虑兰州新区现代有轨电车线网规划的基础上,基于BP神经网络建立现代有轨电车适用性研究分析训练模型,利用Matalab软件实现神经网络学习过程,根据训练结果,对兰州新区现代有轨电车适用性进行评价。
关键词:BP神经网络 有轨电车 适用性
1 BP神经网络适用性评价
1.1 BP神经网络结构
BP神经网络结构形式多样,在一般工程应用中,常采用多层结构形式,BP神经网络结构多层形式主要是由输入层、输出层和若干个隐含层组成的多层感知器,层与层之间的关系是互连的,而同一层单元之间是互不连接的。多层感知器和BP神经网络结构强调的是两个不同的概念,多层感知器是指神经网络结构由相互连接的多层组成,而BP神经网络结构是指神经网络采用误差反向传播的学习算法。但在进行权值调整学习训练时,大多数情况下多层感知器采用误差反向传播的学习算法。从这个角度来讲,多层感知器和BP神经网络结构没有太大的区别,经常指一种网络,即BP神经网络结构。
1.2 BP神经网络结构特点
(1)多层性。BP神经网络是由输入层、输出层和若干个隐含层组成的多层感知器,层与层之间的关系是互连的,而同一层单元之间是互不连接的。
(2)可微性。
BP神经网络的传递函数是线性传递函数,其中x的取值范围为整个实数域,f(x)的取值范围是0到1之间,在具体计算时根据实际情况确定参数范围。
2 BP神经网络应用
BP神经网络是目前应用频率最高的神经网络,其非线性映射能力比较强大,能够集中反映神经网络中最完美的内容[1]。在以前的神经网络训练模型中主要以单层为主,经过多年的发展,多层网络学习训练模型得以实现,而在实际应用中,以BP神经网络学习训练模型为主。
BP神经网络训练模型的传播形式主要有前向传播和误差反向传播两种形式,所谓的前向传播是指对于一个给定的输入模式,先到达输入层再到达隐藏层,在隐藏层经过一系列的处后形成一个输出模式,这种传播模式是一个逐层状态不断更新的过程;所谓的误差反向传播是指在输入输出过程中,期望输出模式和输出响应之间存在一定的误差,不符合输出模式要求,遇到类似情况时,前向传播模式不能继续进行,输出模式会随之转为误差反向传播,在这种模式中,误差值会沿着连接通路分层传至更层级并对误差值进行修正,直至满足要求。BP神经网络训练的过程就是前向传播和误差反向传播不断重复迭新的过程,当精度满足要求时,BP神经网络训练完成,主要包括配置阶段、训练阶段和分类阶段三个阶段,三个阶段之间既相互有区别,又相互之间有着紧密的联系。
3 BP神经网络评价模型的建立
BP神经网络评价模型的建立关键在于网络层数的合理确定和各独立层神经元数的有序配置,前人研究表明,BP神经网络的隐含层应当是一个可以用任意精度表示的连续函数,基于这样的结论,可以将隐含层基本设置为一层[2-3]。
多层单元计算格式按下列式子计算
其中:j=0,1,2,…,M-1
其中:k=0,1,2,…,L-1
式中:
—输入层第i个节点的输出值;
—隐藏层第j个节点的输出值;
—输入层第i个节点到隐藏层第j个节点的权系数;
—隐藏层第j个节点到输出层第k个节点的权系数;
—中间层第j个节点的阀值;
—输出层第k个节点的阀值;
—输出层中第k个节点的实际输出值;
城市规模大小与现代有轨电车应用模式一一对应,不同的城市规模对应着不同的有轨电车应用模式,研究现代有轨电车应用模式就需要对城市规模进行宏观研究,对于现代有轨电车适用性的研究方法很多,本文主要采用BP神经网络方法对兰州新区现代有轨电车适用性进行评价,根据兰州新区现代有轨电车线网规划可知,要建立兰州新区现代有轨电车适用性神经网络模型,按照配置阶段、训练阶段和分类阶段三层合理确定网络层数,确定使用三层BP网络对兰州新区现代有轨电车适用性进行评价,再根据兰州新区现代有轨电车的实际情况,有序配置各独立层神经元数,在大量研究和前人经验的基础上,将输入层节点确定为20个,隐藏层节点确定为15个,神经元输出确定为1个,建立了20*15*1的BP网络神经评价模型。
(1)神经网络输入论域的确定
对于已建立的现代有轨电车适用性评价模型,主要从区域适用性评价、系统适用性评价、技术可行性评价、系统社会效益评价四个方面入手,选择组团匹配性、运能匹配性、速度匹配性、系统造价、线路平纵面、车站布设、线网规划协调、投资效益、土地占用、与其他设施协调性、运营组织、工程实施、车辆技术、线路轨道、供电、技术通用、服务水平、环境影响、景观影响、城市发展20个指标作为神經网络的输入论域。
(2)样本值的建立
本文对现代有轨电车适用性的评价分为5个等级,分别为:差,一般,好,较好,很好;对应值分别为1,2,3,4,5;输出节点的值也对应于此评价结果。
分别选择英国伦敦、美国波特兰、法国巴黎、日本东京、中国北京五个城市现代有轨电车的应用模式,分别定义为样本1、样本2、样本3、样本4和样本5,澳大利亚墨尔本现代有轨电车的应用模式为验证样本,同时确立各输出值。
同时,根据模型精度需要,确定了连个特殊样本:样本6和样本7。
还有两个特殊样本,样本6和样本7。
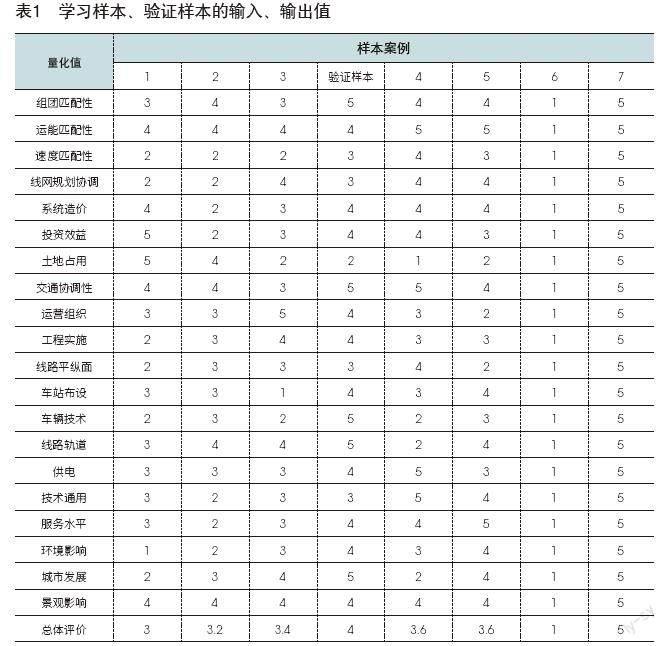
为了方便计算,将所有样本值进行无量纲化,输入输出学习样本和验证样本,可以得到如表1所示的数据。
(3)神经网络学习
为了克服收敛速度慢,难以确定隐层和隐层的节点数,本文采用自适应lr的梯度下降法,这种算法在训练过程中能够合理地改变学习率,合理地避免计算上的缺陷,有利于训练的稳定性,确保了训练速度和精度。本文编制Matalab程序来实现神经网络学习的过程,对兰州新区现代有轨电车适用性进行评价。BP模式训练程序如下:
p=[3 4 3 5 4 4 1 5;
4 4 4 4 5 5 1 5;
2 2 2 3 4 3 1 5;
2 2 4 3 4 4 1 5;
4 2 3 4 4 4 1 5;
5 2 3 4 4 3 1 5;
5 4 2 2 1 2 1 5;
4 4 3 5 5 4 1 5;
3 3 5 4 3 2 1 5;
2 3 4 4 3 3 1 5;
2 3 3 3 4 2 1 5;
3 3 1 4 3 4 1 5;
2 3 2 5 2 3 1 5;
3 4 4 5 2 4 1 5;
3 3 3 4 5 3 1 5;
3 2 3 3 5 4 1 5;
3 2 3 4 4 5 1 5;
1 2 3 4 3 4 1 5;
2 3 4 5 2 4 1 5;
4 4 4 4 4 4 1 5];
net=newff(minmax(p),[15,1],{'tansig','purelin'},'traingdm'); %形成矩阵p,建立隐层15个节点,输出一个神经元的神经网络训练模型
net.trainParam.show=100; %显示中间结果的周期为100
net.trainParam.lr=0.05; %学习率为0.05
net.trainParam.mc=0.9; %网络动量传递系数0.09
net.trainParam.epochs=100; %最大迭代次数100
net.trainParam.goal=1e-10; %训练进度
t=[3 3.2 3.4 4 3.6 3.6 1 5 ];
net=train(net,p,t)
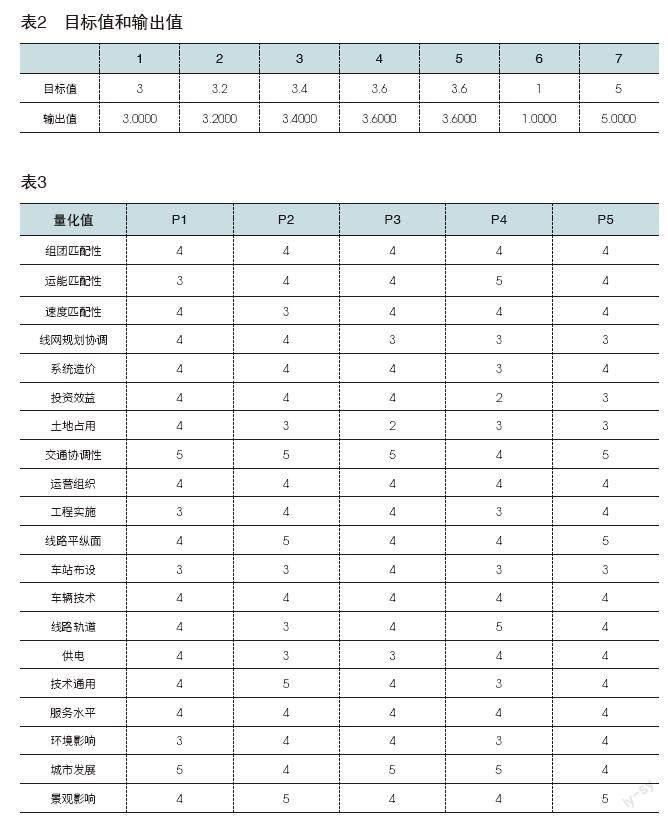
通过学习训练,得到神经神经网络的目标值和输出值,如表2所示。
(4)模型验证
取澳大利亚墨尔本现代有轨电车适用模式对上述训练模型进行验证,其指标无量纲化的值见表2,将数值输入模型进行计算,所得到的数据为3.3350,与目标所得值3.6000相比较,误差很小,模型训练成功。
save chh_net net
P=[4 4 4 4 4;3 4 4 5 4;4 3 4 4 4;4 4 3 3 3;4 4 4 3 4;4 4 4 2 3;4 3 2 3 3;5 5 5 4 5;4 4 4 4 4;3 4 4 3 4;4 5 4 4 5;3 3 4 3 3;4 4 4 4 4;4 3 4 5 4;4 3 3 4 4;4 5 4 3 4;4 4 4 4 4;3 4 4 3 4;5 4 5 5 4;4 5 4 4 5] A=sim(net,p)
A =
3.3350
(5)模型的储存
将上述训练好的神经网络模型(20,15,1)存入知识库中,对其它地区现代有轨电车适用性可以进行评价,只需要输入评价矩阵即可。
4 兰州新区适用性量化评价及结论
根据兰州新区现代有轨电车线网规划的相关信息可知,对兰州新区现代有轨电车适用性评价的参数做无量纲化处理,给出五组评价值,见表3:
量化值输入模型计算,程序如下:
save chh_net net
P=[4 4 4 4 4;3 4 4 5 4;4 3 4 4 4;4 4 3 3 3;4 4 4 3 4;4 4 4 2 3;4 3 2 3 3;5 5 5 4 5;4 4 4 4 4;3 4 4 3 4;4 5 4 4 5;3 3 4 3 3;4 4 4 4 4;4 3 4 5 4;4 3 3 4 4;4 5 4 3 4;4 4 4 4 4;3 4 4 3 4;5 4 5 5 4;4 5 4 4 5];
A=sim(net,p)
A =
3.3350 3.3344 3.3240 3.3198 3.3350
蘭州新区现代有轨电车适用性评价的结果在好和较好之间,充分说明了兰州新区建设现代有轨电车是有必要的。
参考文献:
[1]王艳萍.城市轨道交通线网规划方案评价方法及应用研究[D].北京,北京交通大学,2013.
[2]牟洁.城市轨道交通网络规划综合评价[D].青岛,大连理工大学硕士学位论文,2013.
[3]孟祥定.绿色交通视角下城市轨道交通网络规划决策方法及应用[D].湖南,湖南大学,2007.
