不确定条件下城市地下物流管网布局模型研究

周爱莲，黄雨萌 ZHOU Ailian, HUANG Yumeng

（长沙理工大学 交通运输与工程学院，湖南 长沙 410000）

0 引 言

随着经济和社会的飞速发展，城市物流配送量及配送频率剧烈增长，交通拥堵和环境污染现象也日益严重。在电子商务高度发展的今天，城市物流配送的时效性和高频次性与城市交通拥堵、环境污染、以及城市土地资源可利用性之间的关系是一种悖反关系。在常规的地面交通领域内能够使用的手段和方法不仅极其有限且难以根治。面对这一现状，国内外学者都在积极探索解决城市货运交通问题的有效方式和货运交通未来的发展趋势，针对性地提出了发展立体化城市交通的新思路。试图通过将部分甚至于全部的城市货物运输分流到地下，设计出一种崭新的城市货物运输方式，即构建城市智能地下物流系统（Urban Intelligent Underground Logistics System, UIULS）。

目前日本、荷兰、美国等发达国家针对地下物流系统管网布局方面均展开了一些研究和实践工作。Kosugi[1]从运载工具，通道截面设计和挖掘技术等角度研究了东京地下配送系统的可行性。Pielage[2]从运输车辆选择、货物处理、终端布局、控制系统几个方面探讨了荷兰OLS-ASH 项目的可行性。Delft 和Texas[3]通过比较连通度和经济分析法构建了休斯顿主城区的地下物流系统网络评估模型，选出了最优网络布局结构。曾令慧等[4]将地下物流网络抽象为2 层物流节点，以最大运输能力和最长时间为约束条件，建立了以运输费用和时间最小化的优化模型，采用遗传算法以寻求地下物流网络布局最优。易美等[5]基于客运规划理论预测了城市地下物流网络的货运量数据，考虑了地下物流建设成本高的特点，以物流设施节点、运输管道容量约束和最长管道路径约束为条件，以最低的建设成本、运输成本和中转成本为依据进行建模，并用遗传算法验证了该方法的有效性，为地下物流网络的规划提供了理论依据。

目前，现有的研究成果主要集中在成本目标的控制上，没有对物流需求不确定性的考量和探讨。因此，本文旨在分析城市物流需求与供给动态不确定性特征的基础上，探索构建基于不确定需求的稳健性UIULS 的方法。在不确定环境下对地下物流网络布局进行优化，来缓解交通拥堵、减少环境污染、解决地面交通基础设施的修建扩张和城市土地资源有限的矛盾、帮助节省地下物流网络建设成本以及避免了将来可能出现的扩建成本。

1 模型的构建

1.1 模型场景与假设

不确定性是描述物流需求的动态性特征，随着社会的发展和经济的变革，各类物资的需求量难以准确预测，呈现出不确定的动态变化的特征。此外，物资的需求还会受到商品价格、经济形势以及消费者偏好等诸多因素的影响，导致客户需求不确定，从而引起一段时间内物流需求量的不确定。此现象从历年“双十一”购物节的爆仓及商家利用预售等方法以期提前预估客户需求量可知。

本文拟构造一个UIULS 建设总成本相对较低且对物流需求等因素动态变化不敏感的稳健的地下物流网络体系，该网络采用分层分级的形式，一级节点为城市物流的出入口，将一级节点拟定为城市东南西北部公路运输主要出入口、铁路货运站点、水路运输大型码头港口、机场等[3]；二级节点拟定为城市内部主要的物流园区、配送中心、工业园区、货运枢纽、商贸中心等。一级节点的数量及位置确定，二级节点通过物流与地区经济发展情况、交通位置、产业结构及产业集群、对人口密集区域的辐射能力、地形地质条件、政府政策等因素综合分析选出一系列符合条件的UIULS 二级备选节点。其中一级供需节点之间、一级供需节点与二级供需节点、二级供需节点之间的管道考虑为双向管道。三级节点为居民小区，因物流量由二级节点向三级节点单向运输，可考虑为简单的VRP 问题，本文不再对其进行探究。分层分级形式如图1 所示。

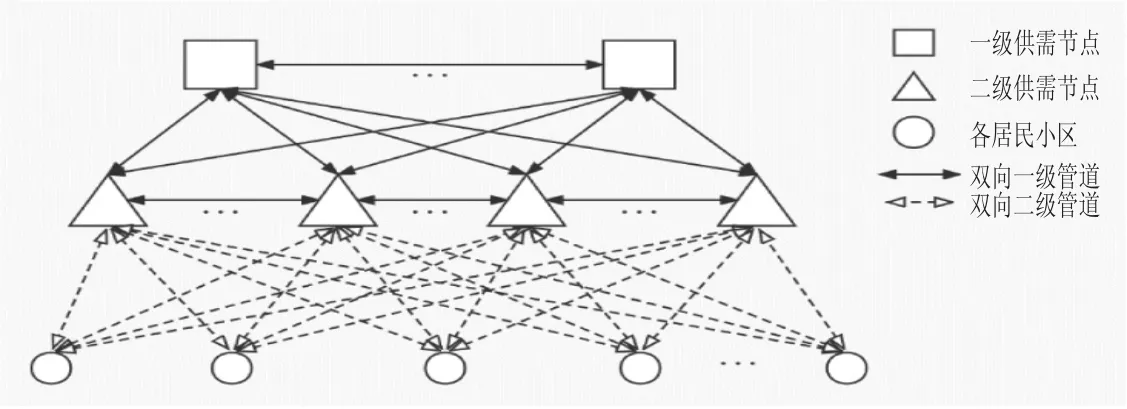
图1 地下物流系统分级图

模型假设如下：

（1） 各需求点的物流需求量随机且扰动系数已知。

（2） 假设管网内只有一种标准运输单元的货物，其储运方式及其运输费率均相同且已知。

（3） 通过初步调查研究得出了各物流供需节点的位置，确定为可在地下开发建设的节点。其中，货运量和每个节点之间的距离是已知的。

（4） 根据地下物流的特性，各个节点之间距离考虑为直线距离。

（5） 根据调查分析，确立了供需节点的层级，将其分为一级供需节点和二级供需节点。不同级别的供需节点具有不同的容量控制，并且有限的容量是已知的。

（6） 一级供需节点之间的管道为主干管道，一级与二级供需节点之间、二级供需节点之间的管道为次干管道，不同级别的管道具有不同的运输能力，其容量包含节点之间的正、反容量，并且管道总容量的上限已知。

（7） 每个供需节点的固定建设成本己知，建设成本与管网长度线性相关，且已知其线性相关度。

（8） 对于标准储运单元的货物，每个节点具有相同且已知的运作和转运成本。

（9） 考虑运输路线的最远距离，即考虑运输最长时间的限制。

1.2 符号含义

设一级供需节点u 的编号为1,2,…,M，而二级供需点v 的编号为M+1，M+2，…，N。

Fu：一级供需节点固定设施的建设成本；Fv：二级供需节点固定设施的建设成本；C：单位货物的管道运输费用；D：单位货物的节点中转或服务费用；：主干管道单位长度的建设成本,k∈U且m∈U；：次干管道单位长度的建设成本,k∉U或m∉U；Lmax：整个管网的最大长度；：为节点之间的管道（k,m ）运输能力的最大容量；：为供需节点k的最大容量。

1.3 模型的建立

考虑到城市物流需求具有较强的动态不确定性特点，而地下管网建设又是一个长期的战略工程。那么如何在动态不确定需求的条件下，构建一个对物流需求变化相对不太敏感的地下管网系统，是决策者需要考虑的核心问题。本文借鉴在机械设计领域“稳健设计”的思想，在分析需求动态特征的基础上，以鲁棒优化为数学工具，构造一个总成本（或其他） 相对较低且对物流需求等因素动态变化不敏感的稳健的UIULS。亦即网络规划模型的目标除了总成本外还要融入体现成本变动状况的稳健性指标。

总成本考虑了管网建设总费用、UIULS 的运营费用两部分，同时本项目拟采用运营费用变动的均方差来体现对布局方案稳健性的考察。参数λ （λ≥ 0 ）表示决策者的偏好，亦即体现决策者关注稳健性的程度。

总成本F （x,y ）最小：

其中，f （x,y ）表示管网建设总费用（或其他），其中包括：

（1） 供需节点建设的固定成本包含一级供需节点和二级供需节点的成本，其成本为：

（2） 管网建设的固定成本包含一级管道的建设成本和二级管道的建设成本，其成本为：

G（x ）表示UIULS 的运营费用。

（3） 运输费用与物流量和运输距离呈正相关，其运输费用为：

（4） 中转费用与供需节点的服务次数和服务量呈正相关，其中转费用为：

1.4 模型的约束条件

其中：约束（6） 表示一级节点和二级节点有其容量的限制；约束（7）、约束（8） 表示一级管道和二级管道有其运输能力容量的限制；约束（9）表示整个地下物流网络系统有其最大的里程限制；约束（10）、约束（11） 表示整个地下物流网络所有的管道是双向的；约束（12）表示都是0~1变量。

1.5 不确定需求的转化

由于城市物流需求具有较强的动态不确定性，很难对各需求点的物流需求量做出准确估计。因此，本文采用相对鲁棒优化方法实现含不确定参数模型的确定化转化，来解决在城市物流需求与供给动态不确定的条件下UIULS 管网布局问题。相对鲁棒优化方法是指将一个控制参数（即约束保护水平） 引入不确定约束条件中，它可以防止数据不确定性模型下的参数不确定性过度影响目标函数的值。通过改变控制参数的值，可以灵活调整模型的鲁棒性以适应解的保守水平。

为此对物流需求量给出如下区间估计：

由于向模型中添加了松弛变量，因此很好地避免了由于扰动范围内物流需求的变化而导致的模型解的不可行性。当γij=0，即时，物流需求的不确定性可以转化为区间下限的确定性；当γij=1，即时，物流需求量的不确定问题可对应为绝对鲁棒问题。这样就可以通过在0 和1 之间调节γij的取值来控制物流需求量的扰动范围，从而平衡不确定模型解的最优性与鲁棒性。

1.6 模型的确立

综上所述，本文所构建的模型如下：

2 物流量分配及模型的GA 求解

2.1 物流量的分配

将城市物流量分配到地下管网中是一个复杂的动态网络在进行不断优化的过程。

其分配模型包括静态多路径法、全有全无分配法、以及容量限制法等。本文拟选用容量限制法中的增量加载分配法，首先，在输入供需表和路权矩阵的情况下，将上述供需表中的每个供需量分成X 份，即将会有X 个供需子表，然后再使用Dijkstra 算法分配供需量x 次。对于每个分配好的供需子表，其路权也会随之修正，直到把所有的供需子表配给路网。

其中：θ 为分配物流量后的路权；θ0为零物流量时的路权；V 为管网的容量承受能力；qs为管网的实际物流量；ω、φ 为路权参数，本文取ω=0.15，φ=4。

2.2 模型的GA 求解

（1） 编 码

本文使用两次遗算法对模型进行求解，先对二级物流供需节点进行求解，使用二进制编码，染色体的长度为备选点数量。每个二级节点将覆盖周边10km 范围内的三级节点，选出满足三级节点覆盖率大于90%的二级节点组合，并将这些结果输入到路网算法中。

路网算法使用值编码的方法对染色体进行编码。染色体的长度将由边的数量决定，假设选择Ln条边，其中：d 为整个路网的平均运输距离，Ln≥n-1。将有N 个供需节点，其编号从1 到N，每两个节点确定一条边。其对应关系与编号，如表1 所示。

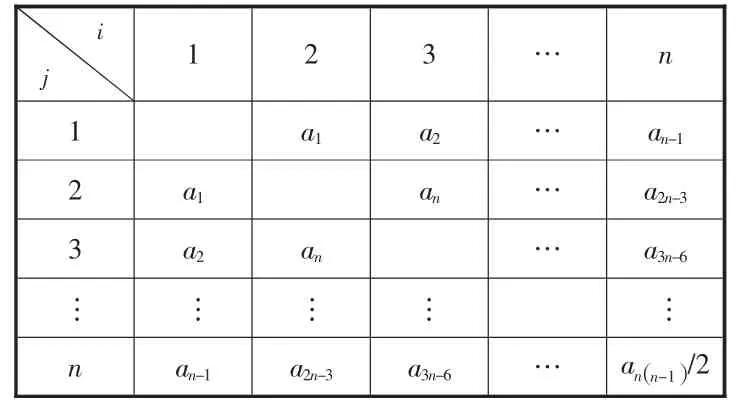
表1 值编码示意表

将节点设为基因进行标号，染色体长度为2Ln，分为Ln个区块，随机生成2Ln个数值大小在[1,N ]内的整数。例如，Ln=6，N=5，染色体为23|12|24|14|45|35|15，对应选中的边为：a5-a1-a6-a3-a10-a9-a4。

（2） 种群规模和适度函数的确定

本文提出的模型种群规模取值为100，该模型求解的是总成本最小化问题，其适应度设置为目标函数的倒数，其适应度为：

（3） 遗传tx 算子的选择、交叉及变异

①选择。通过轮盘赌的选择方式实现最佳保留。

②交叉。使用部分匹配交叉法，随机产生两个交叉点，将这两个点之间的区域定义为匹配区域，并交换两个父代的匹配区域。

③变异。本文采用基本遗传算法的变异方法，根据变异概率在指定的变异点进行变异，并使用其他等位基因替代形成新的染色体。

④停止准则。以最大迭代次数为停止准则，本文选择的最大迭代次数为100 次。

3 实证分析

3.1 参数设置

假设一个城市具备建立城市地下物流系统的条件，通过调查分析将其划分为8 个供需节点，其编号分别为1,2,3,4,5,6,7,8。其中：一级节点为1,2；二级备选节点为3,4,5,6,7,8。各节点之间的距离已知，且为直线距离。算例中各常量取值如表2 所示，各个节点之间的直线距离和货运量如表3 及表4 所示。

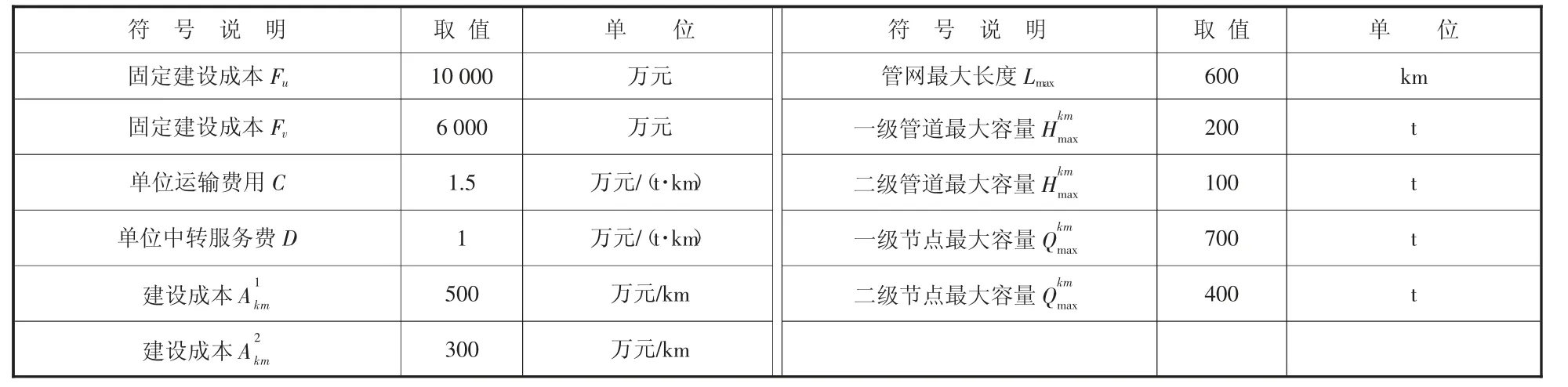
表2 常量取值表

表3 物流量供需表

3.2 结果输出

根据模型算法步骤和相应公式，节点个数n=8，求得整个路网的平均运输距离d=36.70，得出边的数为8.17，根据四舍五入可视为应建8 条管道。其染色体长度为2Ln=16。在模型求解时设定决策者对稳健性的偏好系数λ=1，以物流需求量扰动系数0.2，控制参数0.2 为例，利用Matlab 编程，输出求解结果，其目标函数为548 856 万元。输出的遗传算法的迭代曲线如图2所示。从图2 中可以看出，其迭代曲线在第28 代时收敛。

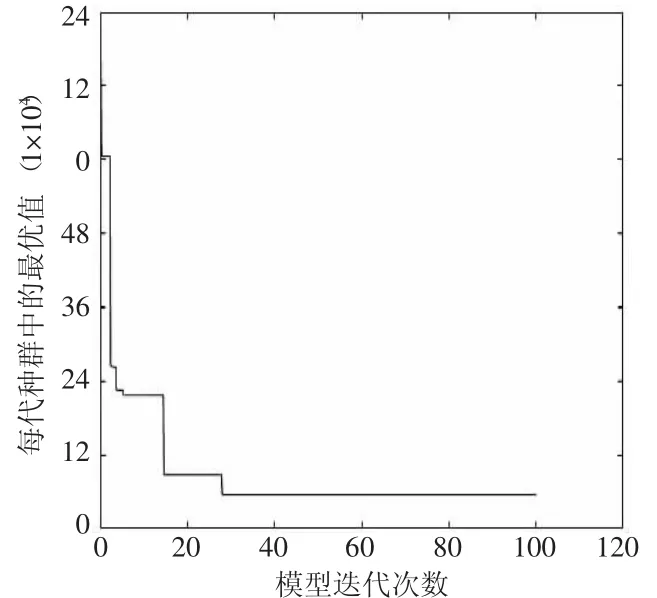
图2 遗传算法迭代图

4 结束语

本文在城市物流需求与供给动态不确定性特征的基础上，对现有的分级地下物流网络进行了改进，借鉴机械领域“稳健系统设计”的思想，以鲁棒优化为数学工具，实现了含不确定参数模型的确定化转换，构建了一个含稳健性指标的城市地下物流网络系统，建立了基于不确定需求的鲁棒UIULS 管网布局模型。该模型能够帮助节省地下物流网络建设成本，并避免将来可能出现的扩建成本。