细观察 析结构 巧配凑

刘海涛

(安徽省芜湖市第一中学 ,安徽 芜湖 241000)

笔者在高三一轮复习的教学中,发现很多看似复杂的数学问题,如果能深究解题目标(式),剖析条件式与目标式间的关联,对条件式(或目标式)进行合理的推理变形,配凑出恰当的代数式,那么便可将问题化繁为简、化难为易,从而轻松解决问题.如何帮助学生掌握该种解题策略呢?笔者以近期的模考题为例,谈“细观察,析结构,巧配凑”在解题中的应用,并在每道例题后给出它的变式问题,以帮助读者检验所学.

1 例析合理配凑在解题中的巧妙运用

1.1 在函数与导数问题中的应用

例1已知函数f(x)=lnx-a(x2-x),若不等式f(x)>0有且仅有2个整数解,则实数a的取值范围是( ).

解析由题得lnx-a(x2-x)>0.

图1 例1解析图

设h(x)=ex(x-2)+x+2,求导,得

h′(x)=(x-1)ex+1,h″(x)=xex>0.

于是h′(x)在(0,+∞)上单调递增,h′(x)>h′(0)=0,则函数h(x)在(0,+∞)上单调递增,h(x)>h(0)=0,于是g′(x)>0,函数g(x)在(0,+∞)上单调递增,且

设φ(x)= ex(x2-4x+6)-2x-6,求导,得

φ′(x)=ex(x2-2x+2)-2,φ″(x)=exx2>0,

于是φ′(x)在(0,+∞)上单调递增,φ′(x)>φ′(0)=0,函数φ(x)在(0,+∞)上单调递增,φ(x)>φ(0)=0,则g″(x)>0,函数g(x)为下凸函数.

解得x0=2,

图2 变式1解析图

当x<1且x≠0时u′(x)<0,当x>1时u′(x)>0,则u(x)在(-∞,0)和(0,1)上单调递减,在(1,+∞)上单调递增.

对于一元二次方程u2-(m+8)u+2m=0,由

Δ=(m+8)2-8m=(m+4)2+48>0,

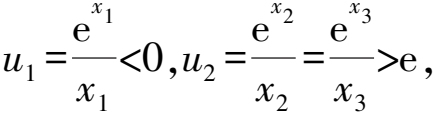
图3 例2解析示意图

=(2-u1)(u2-2)

= -4+2(u1+u2)-u1u2

=-4+2(m+8)-2m=12.

(1)x2的值为____;

(2)m的值为____;

A.e+1 B.e C.e2+1 D.e2

分析首先易知该题无法直接分离参数解答,而由于代数式为指、对函数的混合式,构造函数利用最值解题也难以成功,因此该题考虑根据代数式的特征配凑出同构式解题.

解析不等式ex-aln(ax-1)+1≥0变形,得

x(ex+1)≥axln(ax-1).

配凑得(ex+1)lnex≥axln(ax-1).

构造函数f(t)=(t+1)lnt(t>1),

则不等式等价于f(ex)≥f(ax-1).

则函数f(t)在(1,+∞)上单调递增.

所以a≤g(x)min=g(1)=e+1.

即amax=e+1,故选A.

ex-lna-2-lna-2≥lnx.

即ex-lna-2+x-lna-2≥x+lnx=elnx+lnx.

设φ(t)=et+t,则φ(x-lna-2)≥φ(lnx).

易知φ(t)为单调递增函数.

则x-lna-2≥lnx.

即lna≤x-lnx-2.

ex-lna-2-lna-2≥lnx.

即ex-lna-2+x-lna-2= ex-lna-2+lnex-lna-2≥x+lnx.

设φ(t)=t+lnt,则φ(ex-lna-2)≥φ(x).

易知φ(t)为单调递增函数.

则ex-lna-2≥x.

xex≥ae2x·ln(ae2x).

即xex≥ln(ae2x)·eln(ae2x).

设φ(t)=tet(t>0),则

φ(x)≥φ[ln(ae2x)].

求导得φ′(t)=(t+1)et>0.

所以φ(t)为单调递增函数.

所以x≥ln(ae2x).

所以ex≥ae2x.

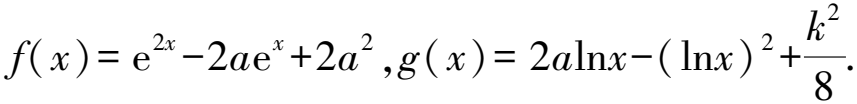
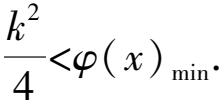
又k∈N*,所以kmax=4.

易知动点A在曲线t(x)=ln(lnx)(x>1)上,动点B在直线l1:x-y=0上.设曲线t(x)上的点P(x0,ln(lnx0))处的切线l2与直线l1平行,则|AB|min即为两平行线间的距离.

于是l2:x-y-x0+ln(lnx0)=0.

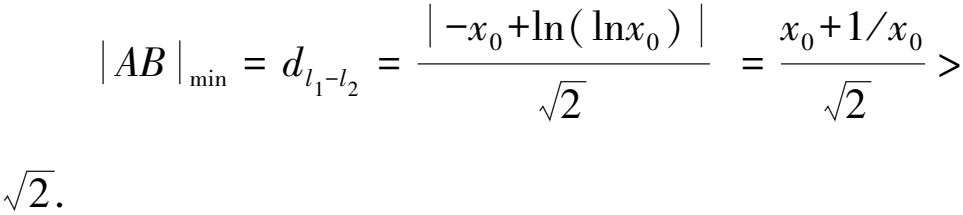
则k≤4,故kmax=4.

1.2 在解析几何问题中的应用

解析由题知F(1,0),若直线l的斜率不存在,则点Q与M,N两点中的一点重合,显然不合题意,则直线l的斜率存在,设l:y=k(x-1),M(x1,y1),N(x2,y2),则K(4,3k).

(4k2+3)x2-8k2x+4k2-12=0.

(2k2+1)x2-4k2x+2k2-8=0.

即5x1+2x2-2=0.

另解由5x1+2x2-2=0,得

则10(x1+x2)2-14(x1+x2)+4=-9x1x2.

2 总结反思

以上例题及其变式难度较大,若采用常规解法解答,则过程繁杂、运算量大,甚至无法解出答案.笔者从代数式的结构特征入手分析,巧妙配凑出目标式的代数形式,或配凑出有利于处理的代数式,降低问题的难度,使解答过程简捷自然.以此展示在有些问题的处理上,根据结构巧妙配凑合理的代数式解题,可以起到事半功倍的解题效果.