从表征到深层理解 从思维到方法建构——多视角破解几何体体积问题

巨小鹏

(陕西省汉中市龙岗学校,陕西 汉中 723102)

立体几何初步知识教学以从整体到局部、从具体到抽象为原则,培养学生的空间想象和数学运算能力.解决立体几何体积问题,可将立体图形转化至平面图形分析,借助学过的几何法、坐标或者向量等数学工具寻找解题方向,从而解决问题.文章以近五年高考试题和模拟试题为例,从公式法、等体积法、分割法、补形法、函数法和向量法等几个方面进行归纳分析,有利于几何体体积问题中知识与方法的系统构建.

1 试题引入

题目(2021年全国乙卷数学文科18)如图1,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,M为BC的中点,且PB⊥AM．

(1)证明:平面PAM⊥平面PBD;

(2)若PD=DC=1,求四棱锥P-ABCD的体积.

图1 2021年全国乙卷数学文科第18题图

2 第(2)问解法探析

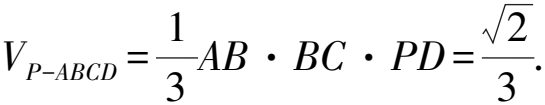
解法2(平面直角坐标系视角)由(1)知AM⊥DB,所以kAM·kBD=-1．

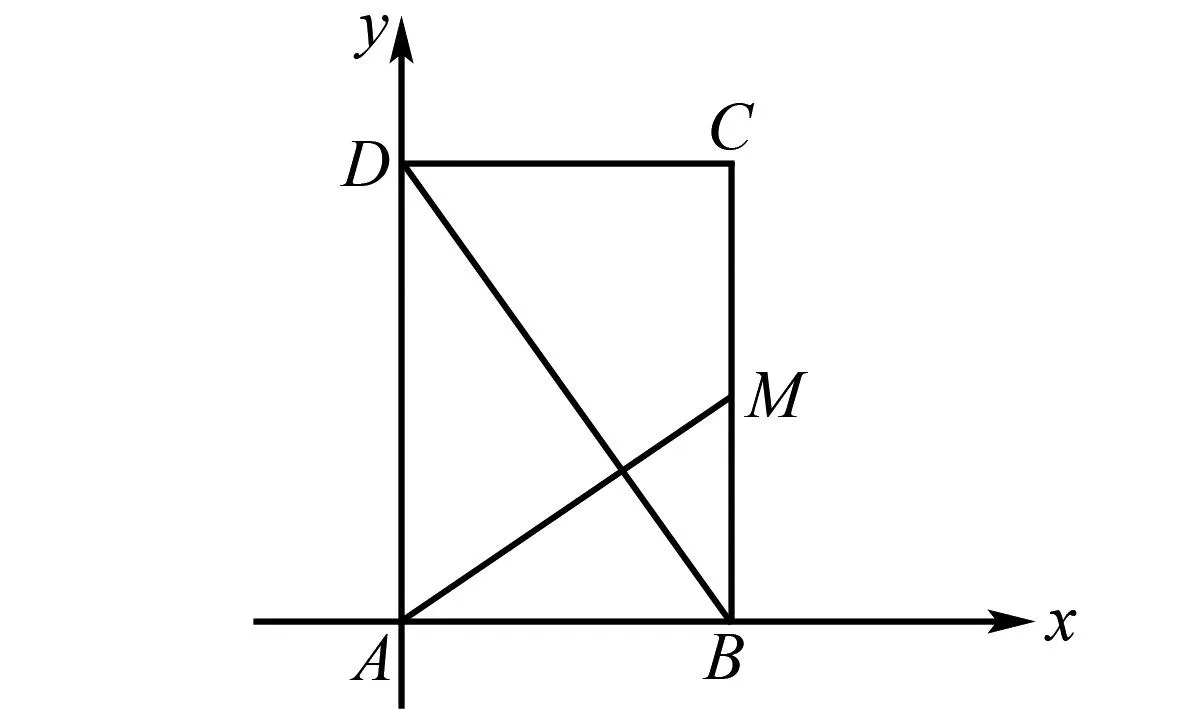
图2 平面直角坐标系视角图

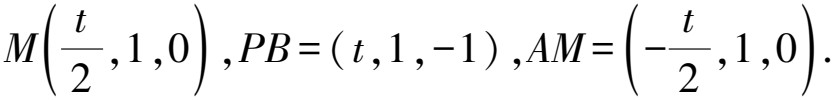
图3 空间直角坐标系视角图

又PD⊥底面ABCD,AM在平面ABCD内,

评注本题破题关键是求出矩形ABCD的边长BC,解法1利用相似三角形求出矩形ABCD的边长BC,从而求得该四棱锥的体积;解法2建立平面直角坐标系,利用直线垂直的条件得到矩形ABCD的边长BC,从而求得该四棱锥的体积;解法3直接利用空间直角坐标系和空间向量的垂直的坐标运算求得矩形的边长;解法4利用空间向量转化求得矩形的边长,所有解法中解法3最为简捷,可见空间向量法在解决立体几何问题中的优越性;解法5直接利用四点向量定理结论得出BC长度,此定理在解决线线角、线面角和二面角问题都有优越性,需要有足够的知识储备[1].

3 求体积问题方法归纳与例析

3.1 直接公式法

解法1 (体积公式视角)如图4,由题意可知点P在平面ABC上的投影在∠BAC的角平分线AD上,记作O,即OP为三棱锥P—ABC的高.

图4 例1解法1示意图

评注本题考查三棱柱的几何特征和体积,考查了基本分析求解能力.往年高考以直接考查公式的试题居多,比如2021年甲卷11题,全国Ⅱ卷第5题,2020年海南卷第13题,2018年全国Ⅰ卷第18题,天津卷文科第11题,2017年全国Ⅰ卷文科第18题,新高考Ⅱ卷文科18题.

3.2 等体积法

评注直接求体积不好求,可以转变角度利用等体积法,等体积法常常解决点到平面的距离问题,是文科常考查的方法.

3.3 分割法

图5 分割成正四面体图图6 例1解法4图

例1解法4(对称平分视角)如图6,取BC中点D,连接PD,AD,则BC⊥PD,BC⊥PD.

所以BC⊥平面APD.

即△PAD为直角三角形.

评注根据对题中几何体几何特征的分析,解法3将分割出以a为棱长的正四面体,根据底面面积之比得出体积,解法4根据三棱锥的几何特征,将三棱锥平分,刚好截面垂直棱,从而利用分割思想解决问题.

例2(2018年江苏卷第10题)如图7所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为____．

图7 2018年江苏卷第10题图

评注解决本类题目的关键是准确理解几何体的结构特征,可以判断所求几何体可以分割为两个全等四棱锥,割补法求几何体体积是比较常规的方法,比如多面体切割成锥体特别是三棱锥,需要有整体与局部结构的意识.

3.4 补形法

例1解法5(补成正四面体视角)延长AP到Q使得AQ=2a,连接QB,QC,则三棱锥Q—ABC是以2a为棱长的正四面体.可知点Q到平面ABC的距离是点P到平面ABC距离的2倍,则

评注解法5相当于是对解法3的一种优化处理,计算更加简单.割补本来属于同一个思想,分割是向内视角,补全是向外视角,但是大多数时候学生都是分割处理,向外的视角不易想到,为了强化此种意识,将割补分为两类进行归纳总结.

例3(2019年Ⅰ卷理12题)已知三棱锥P-ABC的四个顶点在球O球面上,PA=PB=PC,△ABC是边长为2的正三角形,E,F分别是PA,AB的中点,∠CEF=90°,则球O的体积为( ).

解法1 因为PA=PB=PC,△ABC为边长为2的等边三角形,所以P-ABC为正三棱锥.

所以PB⊥AC.

又E,F分别为PA,AB中点,

所以EF∥PB.所以EF⊥AC.

又EF⊥CE,CE∩AC=C,

所以EF⊥平面PAC,PB⊥平面PAC.

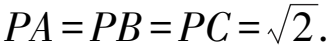
因为△ABC为边长为2的等边三角形.

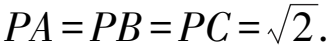
又AB=BC=AC=2,

所以PA,PB,PC两两垂直.

评注本题考查学生的空间想象能力,可通过线面垂直定理,得到三条棱两两互相垂直的关系,进而得到侧棱长,利用补全图形法解决问题.求体积问题有时并非只考查一种方法,有可能公式法和等体积法以及割补法同时考查,需要综合分析解决问题.常见的补全图形比如正六边形放在正方形中,将三棱柱补成平行六面体,三棱锥补成四棱锥或三棱柱或平行六面体,将圆锥放在圆柱体等熟悉的图形中,从而利用整体和全局意识解决问题.

3.5 函数法

例4(2017年全国Ⅰ卷理16题)如图8,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边△ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形．沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥．当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为____．

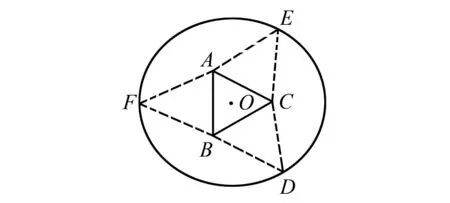
图8 2017年全国Ⅰ卷理科第16题图

解法1 连接OD交BC与点G,设D,E,F重合于点S,正三角形的边长为x(x>0),则

则三棱锥的体积为

设f(x)=25x4-10x5,则f′(x)=100x3-50x4.令f′(x)=0,得x=0(舍)或x=2.

评注利用函数思想,确定函数变量,构造函数求立体几何中的最值问题,特别是利用导函数求取最值,是一次精彩的综合交汇.一般思路是首先要理清数量关系,然后将图形和文字转化为数学语言,建立函数模型,最后通过函数求其最值.

3.6 向量法

例5(2021年新高考Ⅰ卷第20题)如图9,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.

图9 2021年新高考Ⅰ卷第20题图图10 例5解法1示意图

解法1 (坐标向量视角)如图10所示,以O为坐标原点,OA为z轴,OD为y轴,过点O垂直于OD的直线为x轴,建立空间直角坐标系O-xyz.

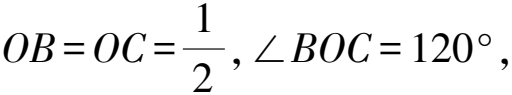
图11 例15解法2示意图

解法3 (二面角的平面角视角2)如图12所示,EG⊥BD,垂足为点G．作GF⊥BC,垂足为点F,连接EF,则OA∥EG．

因为OA⊥平面BCD,所以EG⊥平面BCD,∠EFG为二面角E-BC-D的平面角．

因为∠EFG=45°,所以EG=FG．

由已知得OB=OD=1,故OB=OC=1．

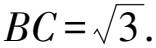
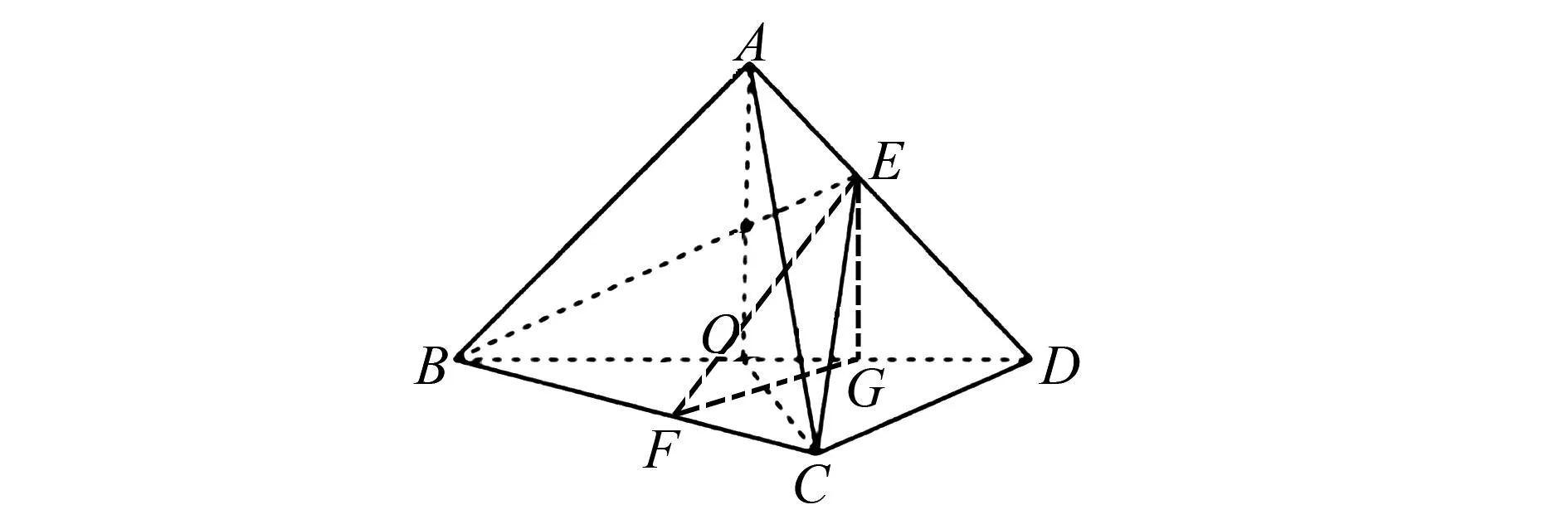
图12 例15解法3示意图

解法4 (三正(余)弦定理视角)如图9记∠EBD=α,∠EBC-β,∠DBC=30°,记二面角E-BC-D=θ．据题意,得θ=45°．对β使用三余弦定理公式,可得cosβ=cosα·cos30°.

①

使用三正弦定理公式,可得sinβsinθ=sinα.

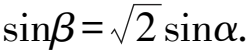
②

评注本题的破题关键是求出OA长度,解法1通过建立空间直角坐标系将几何问题代数化,体现向量的实用价值;解法2作为通性通法找到二面角的平面角,然后对几何体的几何特征进行研究;解法3对解法2对了优化,在本题中属于比较好的方法;解法4中三正(余)弦定理是两个优美的数学公式,在解题过程中如果使用得当会变得更加简单[2].

当然解决此类问题的方法远不止于此,还有平移法、相似比法、祖暅原理法和积分法等.建构主义认为,学生的学习从简单阶段出发,通过逐步渗透,创造出复杂规则或者高级规则的目的是为了解决一个或一类实际问题,然后进入结构化阶段,将离散的图式变得连续起来,再然后进入迁移阶段,达到更为抽象的思维水平,呈现出丰富性、特殊性和发展性的特点.通过认知分析,找到合适的方法,甚至在不同的方法中进行对比分析,将其形成解决此类问题的解题思维体系,会解一类问题即能深层次理解题意,利用结构化思维解决问题.