金属化膜电容器温升计算与优化

王流火，姚成，胡泰山，刘浩

（1.广东电网有限责任公司，广州 510699；2.南方电网科学研究院有限责任公司，广州 510663）

0 引言

常见的金属化膜是在聚丙烯薄膜表面蒸镀一层导电金属层（通常为铝或锌铝复合）作为电极，金属化膜电容器由两层金属化膜卷绕在心轴上，两端喷金作为引出电极。金属层厚度为纳米级别，当介质发生击穿时，金属镀层在电流作用下迅速蒸发，电容器恢复绝缘。由于金属化膜电容器的自愈性能，因此，可工作在较高场强下，具有较高的可靠性[1，6，7，11]。

金属化膜电容器极板薄、电阻大，损耗较大。相对于传统的油浸箔式电容器，金属化膜电容器缺少铝箔、浸渍剂作为导热介质，因此其发热问题远比传统电容器严重。

本文分析金属化膜电容器损耗、发热过程，采用简化电容器模型，计算电容器温升，在此基础上提出电容器的优化设计方法。

1 金属化膜电容器的损耗

金属化膜电容器示意图见图1。

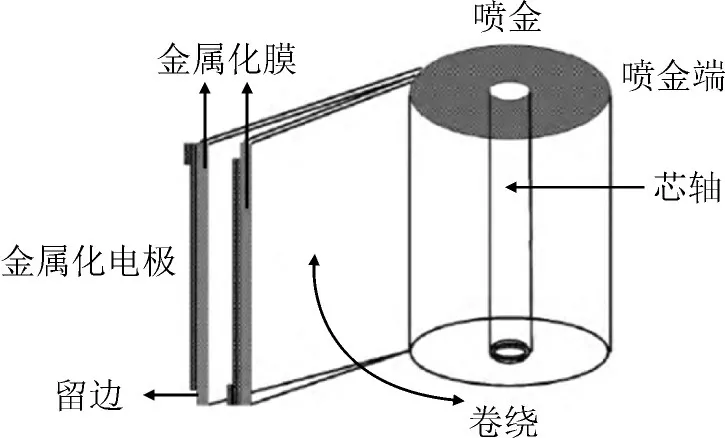
图1 电容器示意图Fig.1 Schematic diagram of capacitor

电容器的损耗主要包括介质损耗与极板（金属镀层）损耗两个部分。其中，聚丙烯薄膜的介质损耗，取决于介质本身特性；电极损耗与电极结构有关，优化损耗主要是优化电极结构[2，9-10]。沿膜宽方向的电容器电流分布见图2，电流I由左端流向右端，并线性下降。电流流过电极时的损耗，可由式（1）计算。

图2 沿膜宽方向的电容器电流分布Fig.2 Current distribution of capacitor along the film width direction

式中：ρ(x)为方阻；L为有效极板长度；c为极板宽度。

电极的等效串联等效电阻ESR 为

沿电容器宽度方向上，由于电极造成的功率分布可以表示为

2 金属化膜电容器内部传热

金属化膜电容器为卷绕结构，具有各向异性，轴向与径向导热系数存在明显差异。如图3 所示，电容器工作时，轴向方向上，热量通过薄膜、金属镀层、气隙并联通道传热；径向方向上，热量通过上述结构的串联传热[12-14]。

图3 电容器导热系数各向异性Fig.3 Anisotropy of thermal conductivity of capacitor

以λF、dF表示聚丙烯薄膜的导热系数与厚度，λM、dM表示金属镀层导热系数与厚度，λA、dA表示空气导热系数与厚度。轴向传热系数可用并联传热介质体系公式计算[3，5]，其等效传热系数近似为

式中，RZn为镀层材料的电阻率。

径向传热系数可用串联传热介质体系公式计算，其等效传热系数近似为

式中，kF、kA分别表示薄膜、空气在总厚度占比。

聚丙烯导热系数为0.22 W/（m∙℃）、金属锌导热系数为116 W/（m∙℃）、空气导热系数近似为0.024 W/（m∙℃）。由于金属层导热系数为聚丙烯导热系数的数百倍，因此，轴向导热系数受到金属层厚度的影响，其与方阻、膜厚有关。径向传热系数与电容卷绕的密实程度有关，通常为一定值，与聚丙烯薄膜导热系数相当[5]。

膜厚为5 μm，轴向导热系数与径向导热系数之比随着方阻变化规律图见图4，轴向导热系数可达到径向导热系数的2 倍以上。

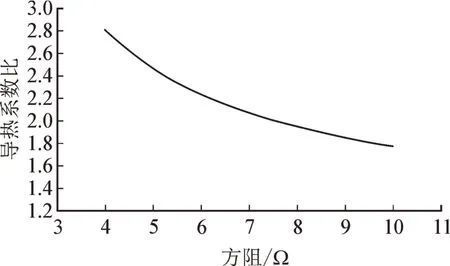
图4 导热系数比随方阻变化规律Fig.4 Variation of thermal conductivity ratio with square resistance

3 金属化膜电容器温升计算模型

电容温升计算模型见图5，其传热方程[4]式（6）为

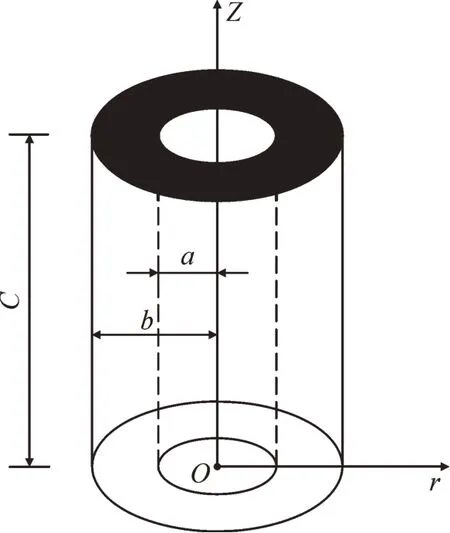
图5 电容温升计算模型Fig.5 Temperature rise calculation model of capacitor

式中：a为芯轴半径；b为电容半径；c为电容高度。

电容传热方程边界条件包括表面温度与心轴绝热条件。为简化计算，不失一般性，近似认为电容表面温度等于平均温度，并将其作为参考温度。

采用变量分离法，可获得电容内部温升计算公式为

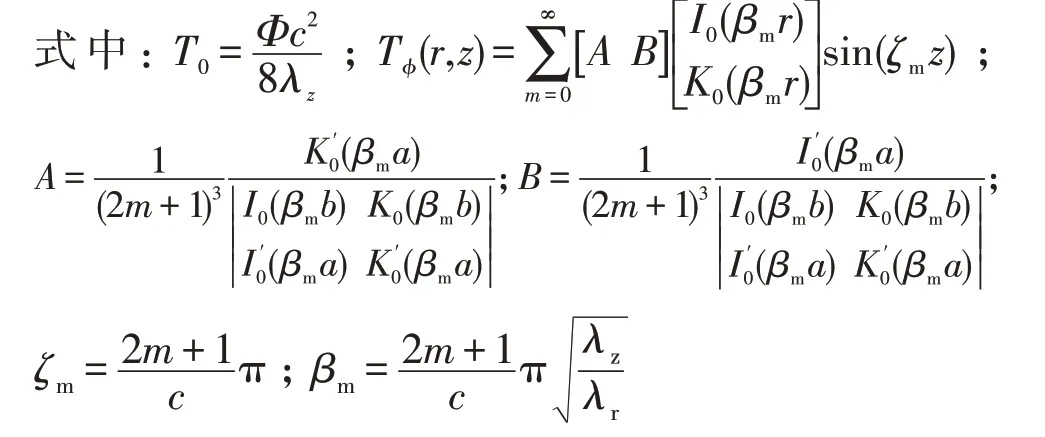
Φ为功率密度；I0，K0分别为第一类修正贝塞尔函数与第二类修正贝塞尔函数。

式（7）的温升公式由两个因子组成：其中极限温升T0，表示沿着径向传热产生的最大温升；第二个因子为轴向导热对温升的修正。

电容量为217 μF，高度为70 mm，心轴直径9 mm，薄膜厚度5.8 μm，方阻8 Ω/□，运行场强57 V/μm的电容器，计算得出的径向和轴向的温升变化情况见图6-7，最大温升约10 K。

图6 电容1/2高度处，沿径向方向的温升Fig.6 Temperature rise along the radial direction at half height of capacitor

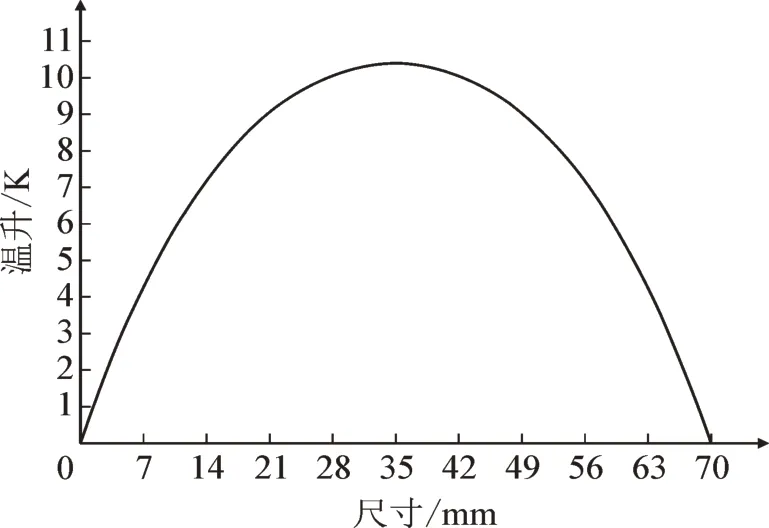
图7 沿心轴轴向的温升Fig.7 Temperature rise along the mandrel

4 金属化膜电容器温升试验对比

试验电容器见图8，试验电容器采用6 μm 薄膜，工作区方阻为50 Ω/□，直径74.5 mm，高度100 mm，电容量36.54 μm，极板长度为303.5 m，元件采用内两串结构每串工作区为42 mm，表面包裹总厚度1 mm铝箔，以减少表面温度梯度。

图8 试验电容器Fig.8 Test capacitor

采用式（1）计算得到电容器在50 Hz 下极板产生的损耗为0.005 3%，聚丙烯薄膜的损耗为0.02%～0.03%，取0.025%估算，介质损耗为极板损耗的5 倍左右。由于这种结构以介质损耗为主，近似认为均匀发热。取电容器损耗为0.030 3%，施加电压为390 V。按照式（7）可计算电容器最热点温升为2.319 ℃。电容器实验与计算温升对比见表1。

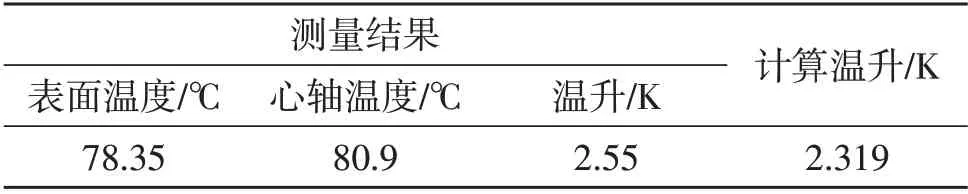
表1 电容器实验与计算温升对比Table 1 Comparison of experimental and calculation temperature rise of capacitor

实测结果电容温升为2.55 K，计算结果为2.319 K，计算偏差-9%。虽然表面采用金属层降低表面温度梯度，但是表面温度不可能完全均匀，热流分布偏差造成计算误差。

5 金属化膜电容器温升的优化

电容器的可靠性由诸多因素决定，如金属化膜的自愈能量、运行电压、运行温度等[20]。相关研究显示，介质材料温度升高8～10 K，其寿命将减少一半[8，16]。相对于油浸式全膜电容器，干式电容器的损耗较大、散热差，温升设计与优化是干式电容器设计的重点工作。基于上述的理论模型对干式电容器损耗与发热进行优化分析。

5.1 镀层结构的优化

镀层结构需要综合考虑自愈能量、损耗等因素。通常方阻越大自愈能量越小，但损耗越大[7]。

常见的镀层结构有3 种结构，见图9。恒定方阻结构，镀层厚度不变；阶梯方阻结构分为两段，其中一部分镀层较厚，一部分较薄；渐变方阻结构，镀层厚度逐渐降低。

图9 金属镀层结构Fig.9 Metal coating construction

1）恒定方阻结构，方阻为常数ρ0；其镀层等效电阻公式为

2）阶梯方阻结构，高方阻为ρH，低方阻为ρL两个部分，公式为

式中，u(x)为单位阶跃函数。

其镀层等效电阻公式为

3）渐变方阻结构，镀层厚度变化与电流密度变化规律一致，方阻逐步变大，即

式中：dMmax为镀层最厚处的厚度；ρmin为该处对应的方阻值。

其镀层等效电阻公式为

基于相同的ESR 对比上述方阻结构的发热功率。若发热功率集中则说明可能出现局部发热过高。按照式（3）分别计算3 种常见方阻结构的功率密度。

1）恒定方阻结构功率密度为

2）阶梯方阻结构

假设高方阻占比50%，等效串联电阻与恒定方阻等效串联电阻相同，那么功率密度为

3）渐变方阻结构

当渐变方阻结构与恒定方阻结构具有相同等效串联电阻时，功率密度为恒定值，为

图10 为电容器在相同ESR 条件下，不同镀层结构的功率分布（归一化）。采用恒定方阻结构端部功率密度较大；采用阶梯方阻结构功率密度最大值出现在中心位置，通常不利于散热；采用渐变方阻结构，发热均匀。

图10 不同镀层结构的功率分布Fig.10 Power distribution of different coating structures

5.2 膜厚对温升的影响

电容器无功功率与场强、介质体积有关。忽略金属化薄膜镀层厚度，无功功率Q与场强E平方成正比、与体积V成正比[3]。考虑膜厚的影响是基于整个的无功功率、镀层结构保持不变，即场强、体积与方阻保持不变。

以渐变方阻为例，总体等效串联电阻为

等效串联电阻随着膜厚度dF的增加将变大。一部分来自于薄膜长度L变短，镀层等效总电阻增加；另一部分由于厚度dF变大，相同体积的电容量变小，总损耗不变，等效的串联电阻将提高。

发热功率密度为

虽然ESR 提高，但电容总体发热功率随着厚度的增加有所降低。表2 为不同膜厚的电容器温升计算值，其高度为70 mm，心轴直径9 mm，直径60 mm，方阻15 Ω/□，运行场强57 V/μm。随着薄膜厚度增加，最热点温度逐步下降。

表2 不同膜厚电容温升Table 2 Temperature rise of capacitor with different film thickness

5.3 膜宽对温升的影响

改变膜宽即调整半径与高度的比例。假设电容的半径与高度之比为bc，采用式（7）计算温升与半径高度比的变化规律，如图11 所示为归一化温度随bc的变化趋势。相同容量的元件，当bc≪1时，元件为细长型，主要热量通过径向传导，由于元件半径很小，温升不高；随着bc的增大，元件通过径向传导的热量降低，元件温升迅速增加；当继续提高bc，元件温升达到峰值后逐渐降低。通常设计的bc值超过其峰值点，因此在空间位置允许的条件下增大bc，可以有效降低温升。

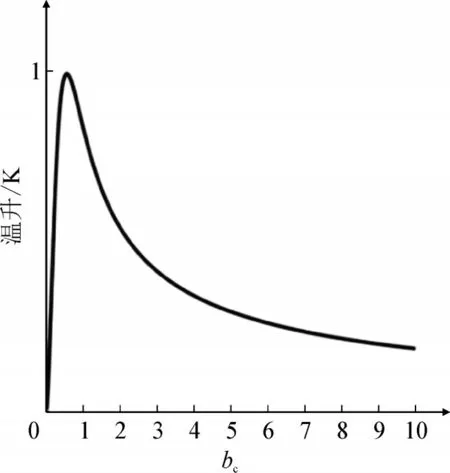
图11 温升随半径高度比不同的变化Fig.11 Variation of temperature rise with different ratio of radius to height

6 结语

文中分析金属化膜电容器的发热、内部热传导过程，通过热传导方程给出电容器表面近似为等温面条件下的温升计算公式，并通过试验验证公式计算的有效性。利用简化计算公式对损耗、热传导系数、以及温升计算公式进行研究，得到如下结论：

1）金属化膜损耗由金属镀层与介质损耗组成，其中金属镀层的损耗、功率密度与镀层结构有关。均匀方阻镀层结构，发热主要集中在端部；阶梯方阻发热集中在中部；渐变方阻发热均匀。在相同ESR 条件下，采用渐变方阻局部温升性能更优；

2）对于场强和容量相同的电容器，功率密度随着薄膜厚度的增加而逐渐降低。主要是由于随着厚度增加，相同容量下电流降低，金属镀层损耗也降低；虽然薄膜导热系数随着厚度增加而降低，但损耗降低的降温作用大于热导率下降的升温作用；

3）对于场强和容量相同的电容器，心子半径与高度比值对温升有显著影响。温升先随着半径高度比的增大迅速增加，然后降低，峰值位置与轴向和径向导热系数之比有关，比值越大，峰值对应的bc值越小。常规的设计中，bc一般在峰值右侧，因此提高bc值可以有效降低最热点温升。