基于自适应主成分分析的CVT 误差状态评估方法
2024-01-10徐其丹刘芳朱明明荣高升鹿晓明李长久
徐其丹,刘芳,朱明明,荣高升,鹿晓明,李长久
(1.国网新疆电力有限公司经济技术研究院,乌鲁木齐 830002;2.国网新疆电力有限公司,乌鲁木齐 830063;3.新疆智诚四方工程造价咨询有限公司,乌鲁木齐 830013)
0 引言
电容式电压互感器(capacitor voltage transformer,CVT)广泛应用于高电压等级的电力系统之中,但受电网频率、二次负荷、环境温度等因素影响,使CVT误差波动性增大,严重影响计量准确性,所以对CVT 的误差状况进行评估具有重要意义[1-4]。在线评估法可以克服传统离线评估法的缺点,无需停电,能反映CVT 的实际工况,但该方法还很不成熟。基于主成分分析的CVT 误差状态评估方法是一种有效的方法,但该方法基于系统静止状态。由于受负荷波动的影响,实际电网是一个动态系统。那么如果应用一个基于静态系统的模型来评估时变系统,将会导致产生较高的误判率[5-7]。指数加权主成分法与移动窗主成分法是目前常用的两种在线监测法。指数加权主成分法通过增加新数据,然后以指数形式不断丢弃旧数据更新主成分模型。该方法的递归特性好,适合时变系统的在线监控。但新数据越多,模型更新速率越慢,监控精度越低;移动窗主成分法采用一个窗口向前推进,不断采集新数据、抛弃旧数据来递归主成分模型,更新速率高。但该方法不能直接对CVT 误差状态进行评估,因为当CVT 出现渐变性故障时其误差也渐变,如果误差变化小于最小可评估度时,移动窗对其变化无法判别,使主成分模型误判率越来越高[8-24]。
为此,本文提出了一种CVT 误差状态在线评估方法。该方法以移动窗主成分法为更新模型基础,结合指数加权移动法,利用窗口部分数据建立主成分模型,通过计算SPE 统计量和控制线来判断误差变化情况。数据更新速度高,评估渐变过程能力强,提高了CVT 误差状态评估精度,算例证明了本文方法的有效性。
1 基于移动窗的主成分模型
1.1 均值、方差、协方差矩阵更新
移动窗原理见图1 所示。通过窗口移动对旧数据进行更新,同时接收新数据,完成窗口更新[25-26]。
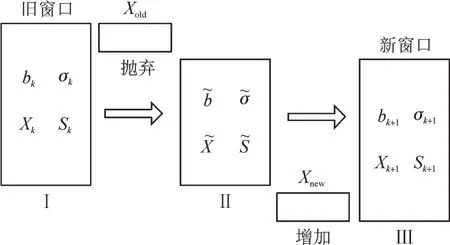
图1 移动窗基本原理Fig.1 Fundamental principles of moving window
在第k时刻,k=0,1,…,k,窗口数据矩阵I 为∈RL×m(L为窗口宽度,m为变量个数),对其进行标准化得矩阵Xk∈RL×m、均值bk∈R1×m、方差σk∈R1×m、协方差矩阵Sk∈Rm×m。
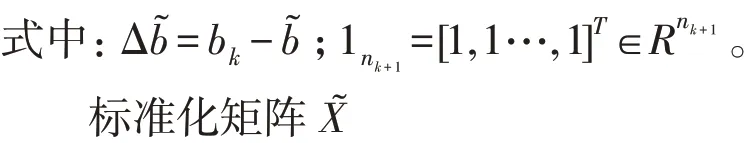
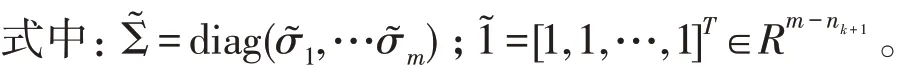
矩阵I 的协方差矩阵Sk
利用矩阵I 的方差递归更新矩阵II 的协方差矩阵S͂。

式中,Δbk+1=bk+1-͂。
将式(5)代入式(7)得协方差矩阵的递归式
1.2 主成分模型空间更新
对第k时刻测量数据的协方差矩阵Sk进行SVD 分解,得主成分模型
将式(9)代入式(8),得
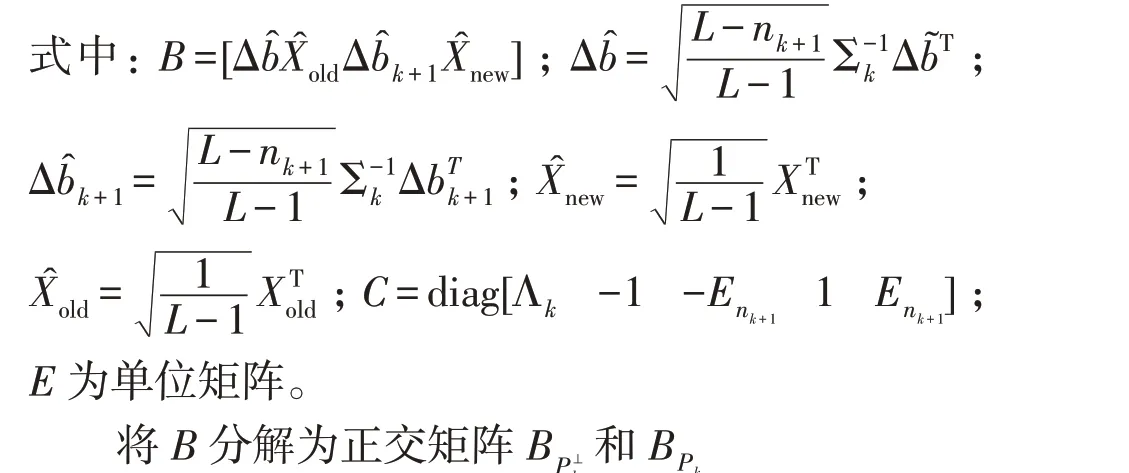
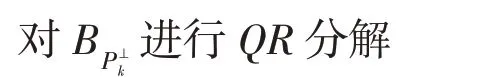
1.3 监控指标更新
根据文献[1],在第k时刻,SPE 统计量和其阈值线公式为[13-14]
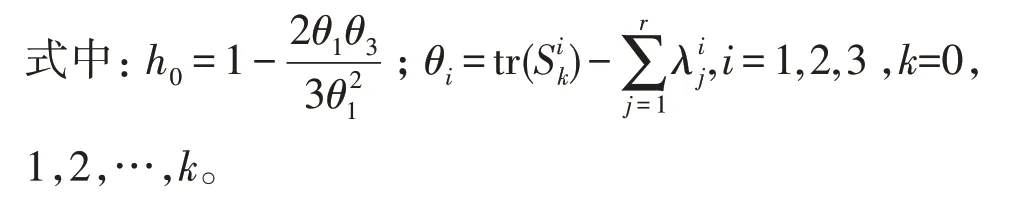
1.4 移动窗部分数据宽度
根据指数加权主成分法原理,可得部分数据宽度

2 基于自适应主成分分析的CVT 误差状态监控
基于自适应主成分分析的CVT 误差状态监控由训练学习和在线监控两个部分组成。训练学习是建立初始主成分模型,确定各种参数;在线监控是对CVT 运行过程进行自适应监控[27-28]。
2.1 训练学习流程
训练学习流程如下:
1)采集正常运行时的三相CVT 二次电压作为样本数据,对样本数据标准化并获取其均值向量和协方差矩阵,建立初始主成分模型;
3)确定α、β、γ等参数以及Lmin和Lw的值;
4)确定‖ Δb0‖和‖ ΔS0‖。通过窗口计算样本数据矩阵的均值向量b和协方差矩阵S。当窗口随着样本数据滑动时,计算‖ Δb‖和‖ ΔS‖。当窗移到数据尽头则停止计算。最后求‖ Δb‖和‖ ΔS‖的平均值‖ Δb0‖和‖ ΔS0‖。
2.2 在线监控
假设在k时刻得到了bk、σk、Sk、Pk、Λk和的值。k+1 时刻采集到了新数据∈R1×3,则
1)分别根据协方差矩阵和主成分模型空间的递归更新过程更新主成分模型;
2)计算‖Δbk+1‖和‖ΔSk+1‖的值;
3)确定移动窗部分数据宽度L;
4)计算k+1 时刻的统计量SPEk+1。若SPEk+1>,判断是否是离群点,如果不是则停止更新并触发异常状态警报;
(5)利用贡献图法判断CVT 计量异常相。
3 CVT误差状态评估
3.1 正常情况下三相CVT误差状态评估
在Matlab/Simulink 平台建立500 kV 三相CVT误差状态评估仿真模型见图2,模型参数见表1。

表1 CVT模型参数Table 1 Parameters of CVT model
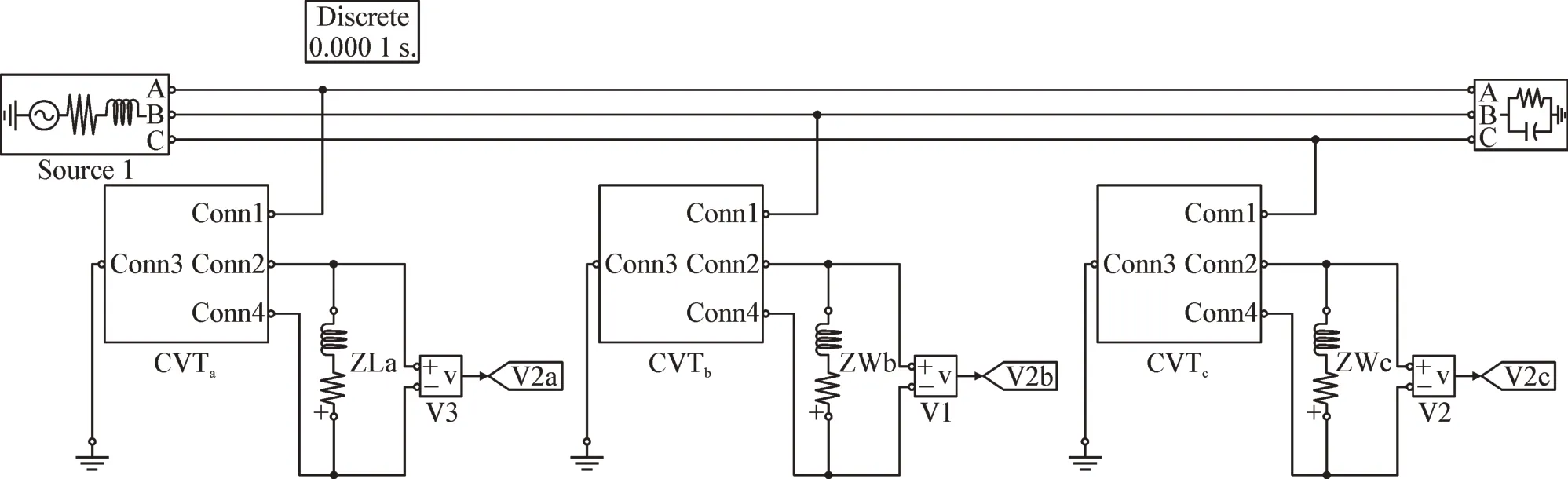
图2 三相CVT误差状态评估仿真模型Fig.2 Simulation model of error state assessment of three-phase CVT
构造一组三相不平衡度三相电压值,不平衡度呈现正太分布,见图3,测试数据共有900 个点。
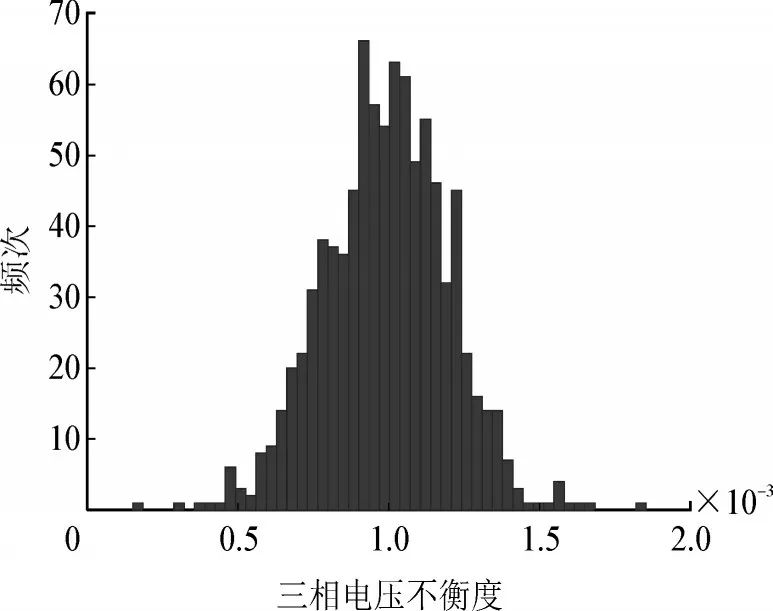
图3 三相不平衡电压Fig.3 Three-phase imbalance voltages
取CVT 正常运行时的二次电压,包括电压有效值和相位值,共100 个点,建立的主成分模型,其SPE统计量监控图见图4。图中相位、电压值的误判率分别为4.78%和18.56%,尤其是在采样点300-600,有大量数据的SPE 统计量超过其控制线。

图4 CVT正常运行时传统主成分分析SPE统计量监控图Fig.4 SPE statistics monitoring diagram of traditional principal component analysis during normal operation of CVT
取Lw=100、Lmin=1、α=0.5、β=0.5、γ=0.4,基于自适应主成分分析方法的SPE 统计量监控图见图5。
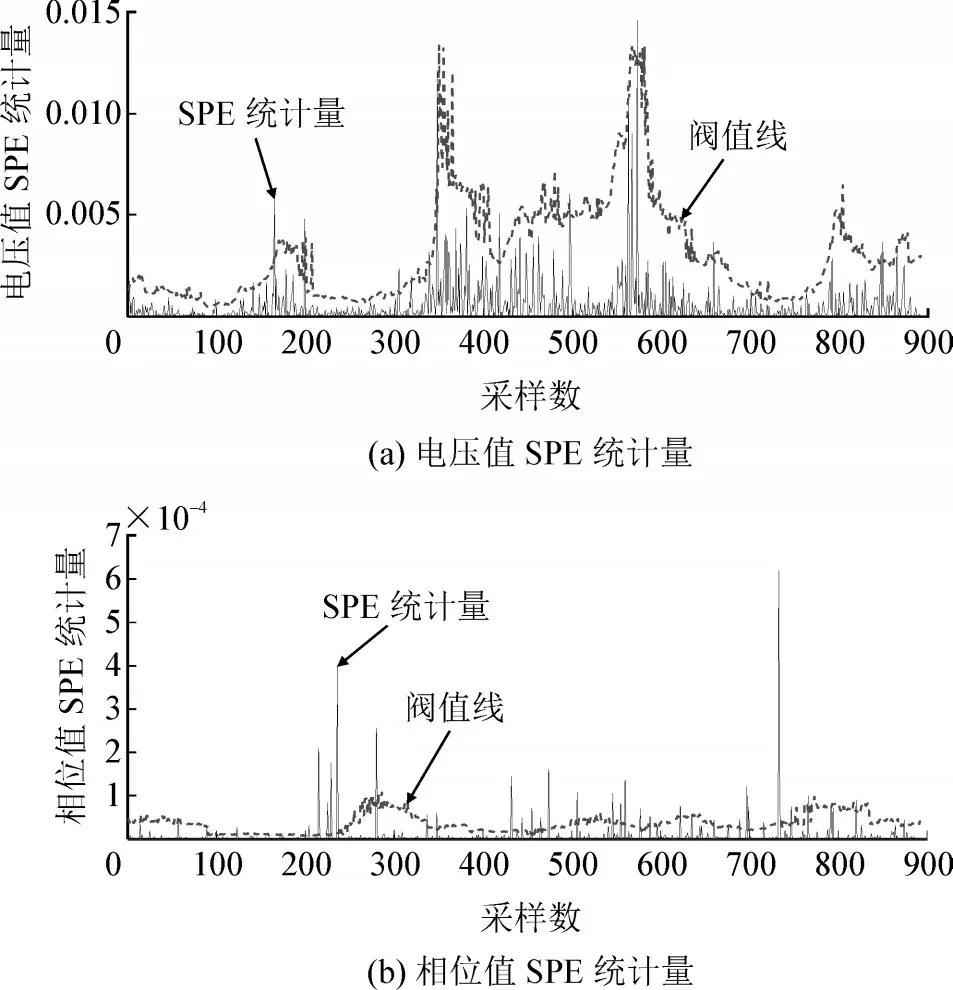
图5 CVT正常运行时自适应主成分分析SPE统计量监控图Fig.5 SPE statistics monitoring diagram of adaptive principal component analysis during normal operation of CVT
由图可见,自适应主成分分析的电压值、相位误判率分别为1.80%和3.03%,误判率大大降低,提高了评估精度。
3.2 CVT误差突变情况下评估
首先采集CVT 正常运行二次电压值500 个点,然后改变CVT 的A 相分压电容值,使得CVT 比差、角差的变化至少大于最小可评估变化0.0618%和1.920′[1],采集二次电压400 个点。SPE 统计量监控图见图6。
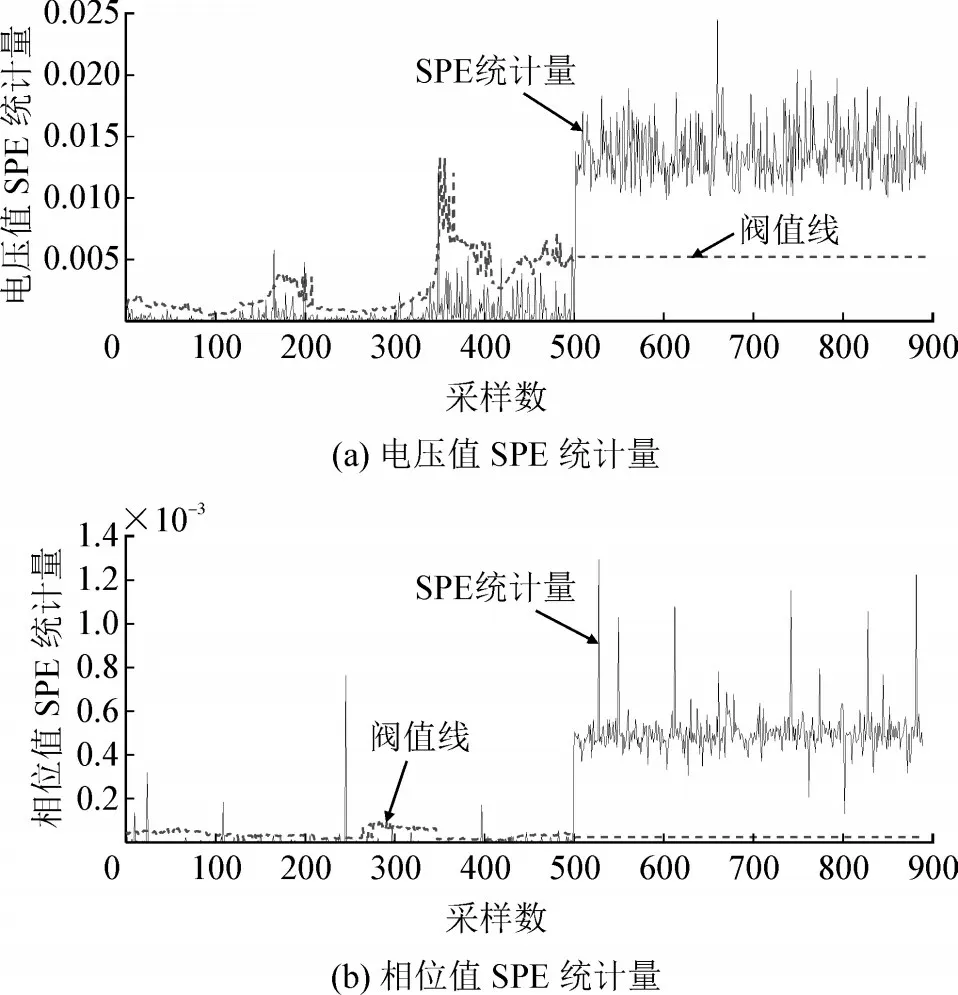
图6 CVT误差突变时自适应主成分分析SPE统计量监控图Fig.6 SPE statistics monitoring diagram of adaptive principal component analysis with sudden change of CVT error
由图6 CVT 误差突变时自适应主成分分析SPE 统计量监控图可见,前500 个点为正常数据,统计量都在控制阈值线以下。CVT 的分压电容值改变导致误差变化,电压和相位SPE 统计量远超阀值线,CVT 误差出现了异常。自适应主成分分析法对CVT 误差突变情况有好的评估效果。
计算每一相测量值对SPE 统计量的贡献,CVT误差突变时自适应主成分分析SPE 统计量贡献图如图7 所示。在500 个点之后,A 相的贡献远大于B、C 两相的,A 相出现了问题。
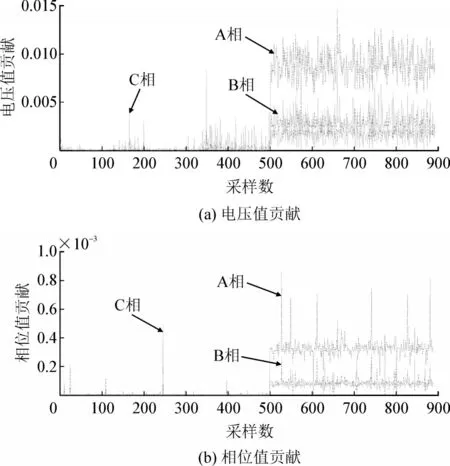
图7 CVT误差突变时自适应主成分分析SPE统计量贡献图Fig.7 SPE statistics contribution diagram of adaptive principal component analysis with sudden change of CVT error
3.3 CVT误差渐变情况下评估
采集CVT 正常运行二次电压500 个点,然后逐渐改变CVT 的A 相分压电容值,采集二次电压400个点。SPE 统计量监控图见图8。图中前500 个点为正常数据,所有数据都在统计控制阈值线以下。从500 个点之后CVT 的分压电容值逐渐改变导致误差变化,控制线随着SPE 统计量的变化而改变。当SPE 统计量逐渐增大最终超过阈值线时,模型停止了更新,表明CVT 误差出现了异常。
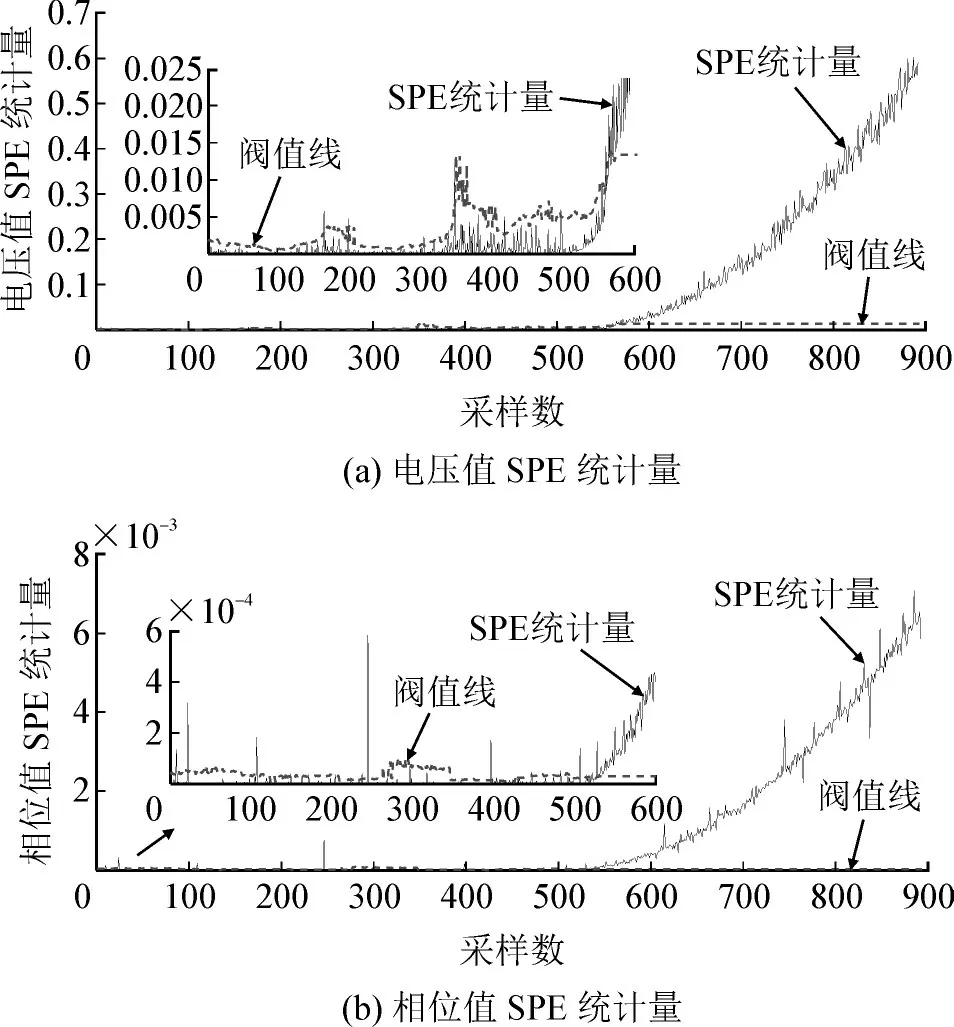
图8 CVT误差渐变时自适应主成分分析SPE统计量监控图Fig.8 SPE statistics monitoring diagram of adaptive principal component analysis with gradual change of CVT error
测量值对SPE 统计量的贡献见图9。图中三相贡献值在前500 个点的贡献基本一样,CVT 运行正常。之后三相贡献都在增大,但A 相的贡献始终远大于B、C 相,表明CVT 误差出现异常且A 相出现了问题。
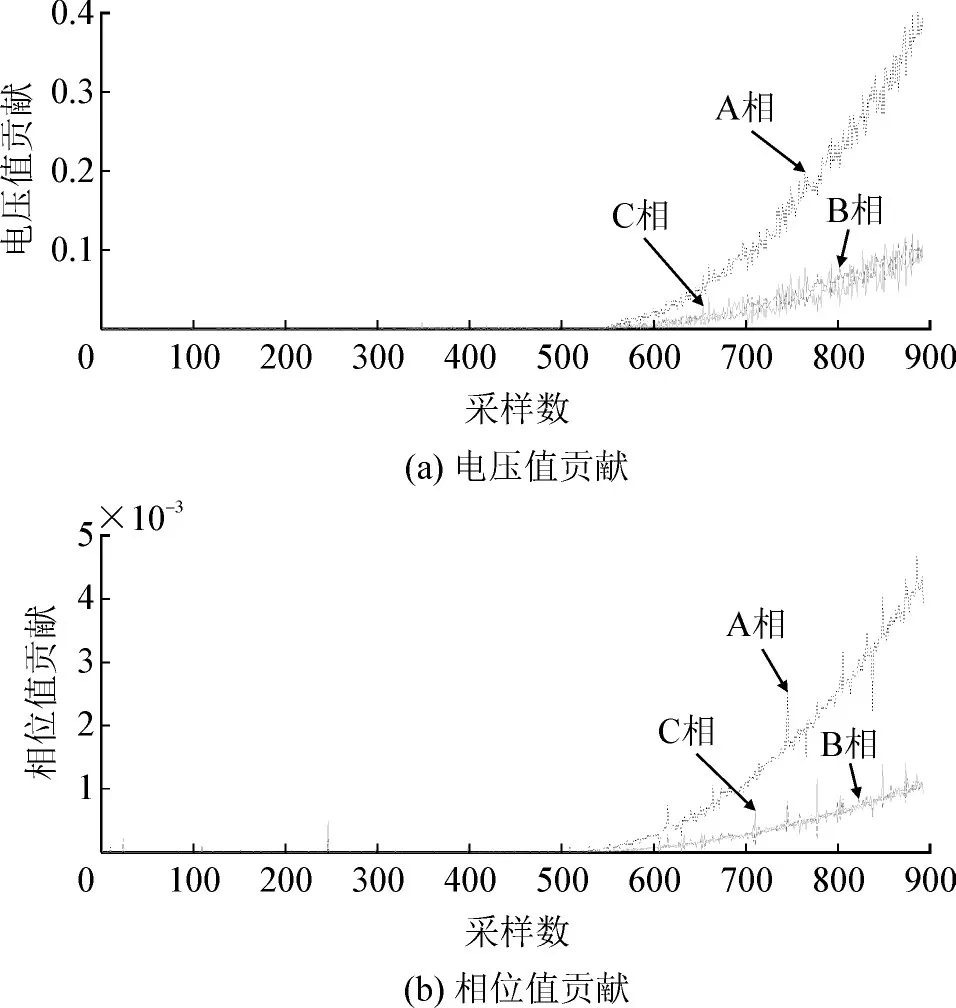
图9 CVT误差渐变时自适应主成分分析SPE统计量贡献图Fig.9 SPE statistics contribution diagram of adaptive principal component analysis with gradual change of CVT error
4 结语
针对传统的主成分分析法在对CVT 误差状态评估时,由于电力系统的时变性导致评估误判率较高的问题,提出的自适应主成分分析法,是一种基于移动窗主成分法并结合指数加权主成分法的CVT 误差状态评估法。该方法利用窗口部分数据建立主成分模型,通过计算SPE 统计量和控制线来判断误差变化情况。研究结果表明,相比于传统主成分分析法,本文方法可以将电压误判率从18.56%降为1.80%,相位误判率从4.78% 降为3.03%,有效减少电力系统波动引起的评估误判率,极大提高了CVT 误差状态评估的准确率。
