基于主成分分析的CVT 误差状态评估

郭丽娟，高宝琪，陈丽，门艳，崔翔

（1.国网新疆检修公司，乌鲁木齐 830002；2.国网新疆电力有限公司，乌鲁木齐 830063；3.国网新疆电力有限公司经济技术研究院，乌鲁木齐 830002）

0 引言

互感器是电量信号采集的关键设备，对于电能计量的准确性具有很大的影响。电容式电压互感器（capacitor voltage transformer，CVT）以其占地面积小、绝缘性能好等特点而广泛应用于高压系统之中。但由于CVT 受电网频率、二次负荷、环境温度、外电场等多种因素的影响而产生较大的误差波动性，严重影响电能计量的准确性[1]。

传统的CVT 误差状态评估是离线评估法[2～3]。该方法原理简单，但不能反映实际工况的误差状态，且评估周期长，严重影响了电力系统的稳定运行。随着智能电网的发展，CVT 误差状态在线评估成为研究热点。目前国内外对电力互感器误差状态的在线评估方法做了大量的研究，主要有比较法、专家系统法、模型解析法、信号分析法等。这些方法各有特点，但受复杂电磁环境的影响，评估准确性和应用范围受到了限制[4～15]。本文针对电网频率、二次负荷、环境温度、外电场等因素对CVT 误差状态的影响，提出了基于主成分分析的在线评价CVT 误差状态的方法。该方法首先通过主成分分析把CVT 的二次电压采样数据进行分解，得到主成分空间与残差空间。然后将CVT 的误差状况映射到残差空间，并计算测量数据的平方预测误差（squared prediction error，SPE）统计量，根据SPE 统计量和控制线判断CVT 的误差状况。该方法能够准确评估出CVT 误差正常、突变、渐变等不同状况，仿真结果验证了本文方法的准确性，为在线评估CVT 误差状态提供了一种理论方法。

1 主成分分析的基本原理

主成分分析就是将一组可能存在相关性的变量转换为一组线性不相关的变量（主成分），目前在数据压缩、图象处理、奇异值检测、变量分类及工业过程监控等方面得到了广泛应用[14-18]。

1.1 主成分空间与残差空间

假设样本数据集X0∈Rn×m，其中n代表样本的测量个数，m代表样本的变量个数。对X0进行标准化处理，得

式中：μi、σi(i=1,2,…,m) 分别为样本每一列的平均值、标准差；x为样本测量值。

将式（1）进行分解

将式（2）表示成矩阵形式

式中：T=[t1,t2,…,tm]为得分矩阵；P=[p1,p2,…,pm]为负荷矩阵。

分解式（3）

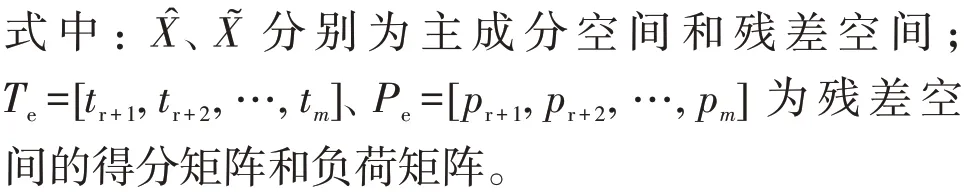
将三相CVT 的二次侧电压值或相位值作为测量样本数据，利用主成分分析法将其分解为主成分空间与残差空间。那么，主成分空间将体现电网电压的波动变化，而残差空间体现CVT 误差的波动变化。

1.2 主元数的确定

主元数r通常是根据计算前r个主元累计方差的百分比是否大于某一个期望值来确定。其计算公式为

式中，P是由经验所得的一个期望标准，通常取为85%。

主成分空间反映了过程变量期望值的变化程度，残差空间反映了过程变量噪声波动的变化程度。

1.3 SPE统计量

由上述分析可知，若将三相CVT 的二次电压值作为测量样本，利用主成分分析法将其分解为主成分空间与残差空间，则主成分空间与残差空间能够分别反映电网电压和CVT 误差的波动变化。如果CVT 出现了故障，则其误差就会发生变化，这时测量样本数据在残差空间的映射就会改变。因此，衡量映射的改变程度就可以判断出CVT 的误差是否产生了问题。SPE 统计量是衡量映射改变程度的常用指标。

式中：λi为测量数据矩阵X的协方差矩阵的特征值；Cα为标准正太分布在置信水平α下的阈值；r为主成分个数；m为变量个数。

1.4 CVT误差变化异常状态辨识

式中：Ii为单位矩阵的列向量；i为样本的测量个数；x(t)为在t时刻三相CVT 二次侧的测量量值。

由（10）式得，贡献值较大的变量即为异常原因变量。

2 CVT误差状态评估流程

CVT 误差状态评估流程如下：

1）采集CVT 常态时二次侧的运行电压值数据矩阵X；

2）对矩阵X进行SVD 分解，得到X的特征值λi(i=1,2,…,m)及特征向量pi(i=1,2,…,m)；

3）根据式（7）确定的主元个数，同时根据r值确定特征值向量组成的矩阵Pr和矩阵Pe；

4）根据式（9）利用合适的置信度水平α计算SPE 统计量的阀值线，以此判断CVT 的状态。如果统计量未超过阀值线，则表明CVT 正常，否则判断CVT 异常；

5）根据式（10）计算每一相的贡献度，贡献值最大的一相即为故障相。

3 仿真分析

3.1 正常情况下CVT误差状态评估

建立500 kV 三相CVT 误差状态评估Matlab/Simulink 模型见图1，频率50 Hz 误差小于0.2 Hz。CVT 等效电路见图2，CVT 模型参数见表1。

表1 CVT模型参数Table 1 Parameters of CVT model

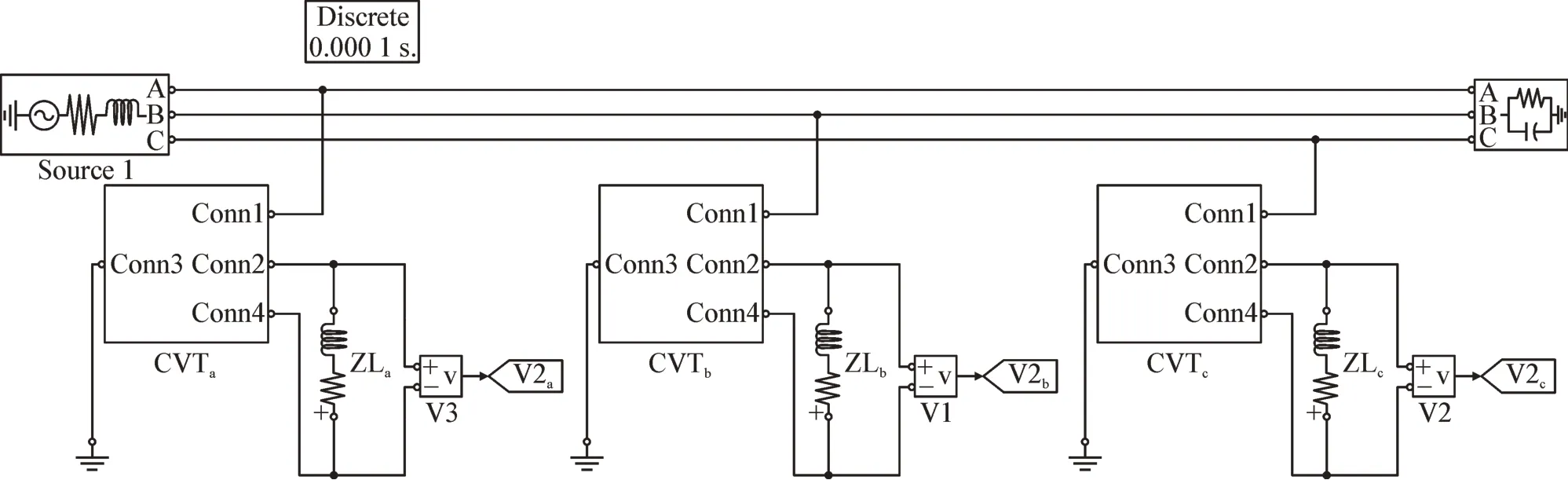
图1 三相CVT误差状态评估仿真模型Fig.1 Error state assessment simulation model of three-phase CVT

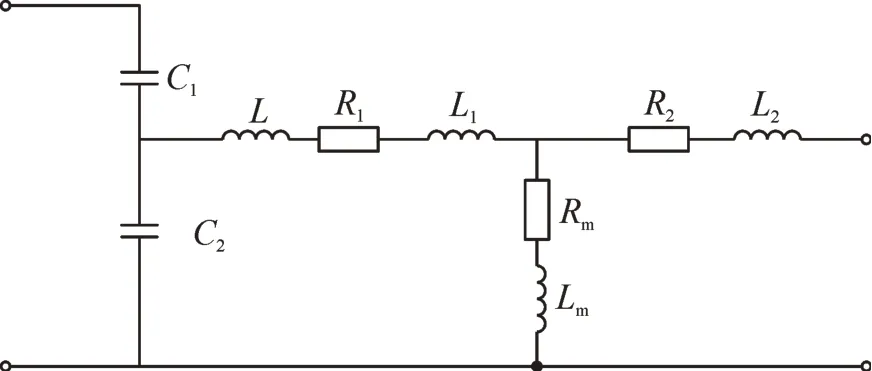
图2 CVT等效电路Fig.2 Equivalent circuit of CVT

图中：C1、C2为CVT 分压电容；R1、L1为一次绕组电阻、电感；R2、L2为二次绕组电阻、电感；L为补偿电抗器电感；Rm、Lm为激磁电阻与电感。

根据CVT 误差状态检测流程，首先采集CVT正常运行时的二次电压数据共集100 个点。当置信度水平为99%时，主成分模型参数见表2。

采集正常运行时的CVT 二次电压共500 个数据点。采样点的比差、角差变化不超过0.061 8%和1.920（最小可评估变化值）[15]。对采集数据使用主成分模型计算SPE 统计量，统计量监控图见图3。图中绝大部分的SPE 值都小于阈值线，电压误判率小于3.4%，相位值误判率小于1.6%。

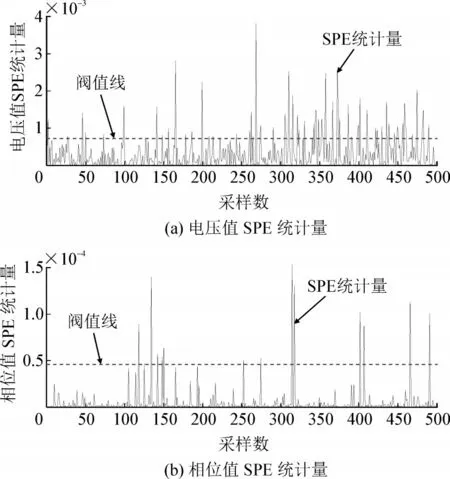
图3 CVT正常运行时SPE统计量监控图Fig.3 SPE statistics monitoring diagram during normal operation of CVT

3.2 CVT误差突变的评估

首先采集CVT 正常运行时二次电压数据250个点。然后改变CVT 的A 相分压电容值，使CVT比差、角差变化至少大于最小可评估变化值；再采集250 个点，SPE 统计量监控图如图4 所示。由图可见，前250 个点为正常数据，所有的数据都在统计控制阈值线以下。在250 个点之后CVT 的分压电容值改变导致误差变化，SPE 统计量远超阈值线，说明CVT 出现了故障。

测量值对SPE 统计量的贡献如图5 所示。

由突变情况下测量数据对SPE 统计量的贡献图5 可知，在250 个点之后，A 相的贡献远大于B、C 两相的贡献，说明A 相出现了问题。B、C 两相的贡献大于正常时的贡献。这是因为当CVT 的某一相出现问题时，测量数据构成的矩阵变换到残差空间中会影响其余两相的映射长度，其长度会向一个方向增加，这就导致了B、C 两相的贡献也增加了，但正常相贡献的增加总是远小于故障相的增加。

3.3 CVT误差渐变情况下评估

首先采集CVT 正常运行时二次电压100 个点，然后逐渐改变CVT 的A 相分压电容值，使CVT 的误差逐渐增大，再采集400 个点。采集数据的SPE监控图见图6。渐变情况下CVT 的SPE 统计量监控图中，前100 个点为正常数据，所有的数据都在统计控制阈值线以下。在100 个点之后CVT 的分压电容值逐渐改变导致误差变化，SPE 统计量也逐渐增大，最终超过了阈值线，说明CVT 出现了故障。

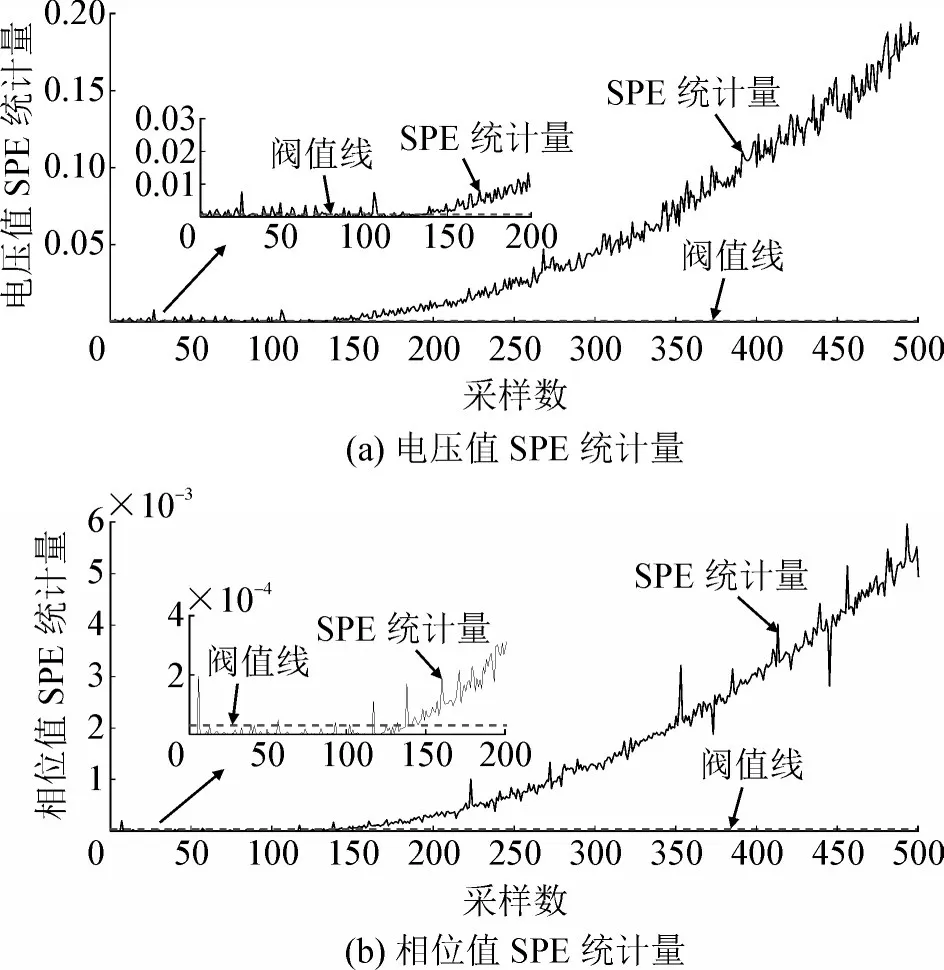
图6 渐变情况下CVT的SPE统计量监控图Fig.6 SPE statistics monitoring diagram of CVT under gradual change

测量值对SPE 统计量的贡献如图7 所示，渐变情况下测量数据对SPE 统计量的贡献图中CVT三相的贡献值在100 个点之后都在逐渐增大，但是A 相的贡献始终远大于B、C 相的，表明A 相出现了问题。

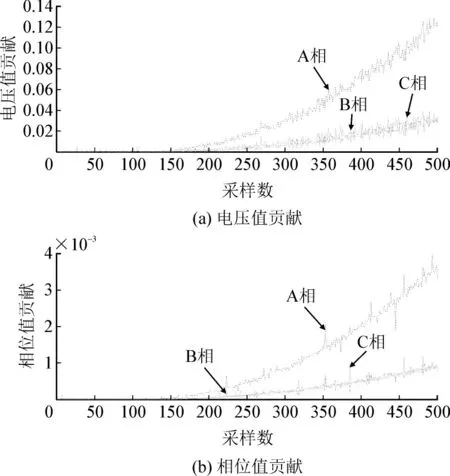
图7 渐变情况下测量数据对SPE统计量的贡献图Fig.7 Contribution diagram of measurement data to SPE statistics under gradual conditions

4 结语

在CVT 误差状态评估中，本文提出的应用主成分分析法于在线评估CVT 误差状态的方法，是通过CVT 的二次电压，将CVT 的误差状态映射到残差空间中，再根据SPE 统计量和控制线判别误差状态。通过对500 kV CVT 进行仿真分析，结果表明，本文方法能评估出比差的最小变化为0.061 8%、角差的最小变化为1.920′，并对CVT 误差突变、渐变等情况均能进行准确评估，是在线评估CVT 误差状态的一种有效方法。