基于轴对称四边形薄导体模型的电阻估算法
2016-04-23薛芃,昝鑫,邹军
薛 芃, 昝 鑫, 邹 军
(清华大学 电机工程与应用电子技术系, 北京 100084)
基于轴对称四边形薄导体模型的电阻估算法
薛芃, 昝鑫, 邹军
(清华大学 电机工程与应用电子技术系, 北京 100084)
摘要:本文提出一种利用轴对称薄片导体模型近似等效处理不规则的薄片导体转角电阻的估算方法。首先从理论出发,论证了所有轴对称的四边形薄片导体,其对边之间的电阻等于其方阻。以该结论为依据,得到了一种以近似划分为手段的薄片电阻估算法。作为实例,将该方法应用于L型薄片电阻的估算,并对这种估算的有效性和精确性进行了分析和讨论。
关键词:电阻估算;薄片电阻;方阻
0引言
薄片导体材料在现今的生产生活中并不罕见。对于形状不规则的薄片导体的电阻,求得解析解往往比较困难。要精确求解往往采用实验模拟法获得或利用软件进行数值求解。然而这些方法较为繁琐,因此对精度要求不高的场合,也可用估算的方法。
此前已有一些估算法,如利用圆弧导体等效处理进行估算,也在特定场合取得了较好的效果[1]。本文提出一种新的估算方法,利用关于对角线轴对称的四边形薄片导体,其对边间电阻等于方阻的性质,将原不规则图形近似划分为矩形与轴对称四边形薄片导体进行估算方法。
该方法思路明确且计算简单,同时相较传统估算法具有更高的精度,具有较好的普适性。
1轴对称薄片导体的电阻计算
1.1方块电阻
对于边长为a,厚度为h,电导率为γ的方形薄片导体,可知其对边间的电阻为
R=a/γha=1/γh
(1)
方形薄片的电阻只和材料与厚度有关,该电阻称为方块电阻。
1.2四边形薄片导体的电阻
对于如图1的四边形平面导体,形状不规则,难以直接求解其对边间的电阻。

图1 四边形薄片导体
由于h很小,可认为电场为平行平面场。若在AB边与CD边之间加电压U,以CD边为电位零点,则导体内,电位满足
▽2φ=-▽·E=0
(2)
导体边界上,边界条件为
φ|AB=U
(3)
φ|CD=0
(4)
∂φ/∂n|AD、BC=0
(5)
为推导方便,在导体区域内构建如下矢量场
E2=E×k
(6)
其中k是z轴正向单位矢量。则E2也在x-y平面内,可证其在导体内的旋度为
▽×E2=▽×(E×k)=0
(7)
说明E2在电阻区域内是无旋场,则可构建势函数φ2,使之满足
E2=-▽φ2
(8)
又可得
▽2φ2=-▽·E2=0
(9)
说明φ2在区域内部满足拉普拉斯方程。又由于E2与E处处垂直,则φ2的边界条件为
φ2|AD=C1
(10)
φ2|BC=C2
(11)
∂φ2/∂n|AB、BD=0
(12)
其中C1、C2为常数。
可看出,此时的φ2与E2能对应另一种电场模型,即不在AB边与CD边之间加电压,而在AD与BC边之间加电压。
在AB边与CD边之间加电压U时,有
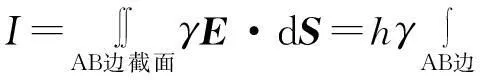
(13)
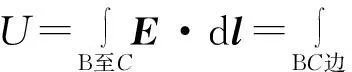
(14)
与之类似,在AD与BC边之间加电压通电时,则有
(15)
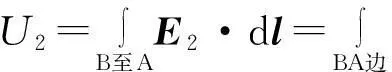
(16)
E与E2分别为矢量的模,由在式(6)对E的定义可知有E=E2。则有
U=I2/γh
(17)
U2=I/γh
(18)
则在两种情况下,导体分别对应的电阻之间满足
(19)
R方即方块电阻,式(19)说明:分别在其两组对边间施加电压时对应的两个电阻值,其乘积为方块电阻的平方。
1.3轴对称薄片导体的电阻
如图2所示,当四边形薄片导体关于某条对角线轴对称时,应用上述结论,又由对称性有
R1=R2=1/γh=R方
(20)
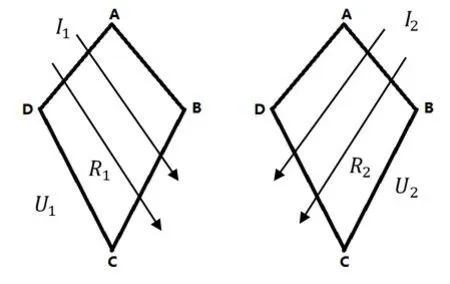
图2 轴对称薄片导体对边间电阻
说明轴对称四边形薄片导体,对边间的电阻即方块电阻。
2L型薄片电阻估算
2.1直角转角L型薄片导体电阻估算
如图3,考虑如下宽度相等直角转角的L型薄片导体,AB=DF=BC=CD,∠AEF=90°,设AB=L,薄片电阻厚度为h,电阻率为γ。

图3 直角转角L型薄片导体
估算在AB边与DF边间加电压时的电阻。
对L型薄片电阻进行近似等效。如图4所示,利用对称性,连接CE,取L型薄片电阻的一半ABCE考虑,过E作∠AEC的角平分线,过C作∠BCE的角平分线,两线交于G点。过G分别作AE的垂线与AE、BC分别相交于H、I点,再过G作EC的垂线交于J点。由几何知识可得,GH=GI=GJ=0.5L,RtΔGEH≅RtΔGEJ,RtΔGCJ≅RtΔGCI。
对图形另一半作相同处理。

图4 直角转角 L型薄片导体的分割
由于线段HI离转角有一定距离,则可近似是等势线。由于线段GJ主要落在转角部分而且与等势线CE垂直,则可近似认为是一条电流线。
经过以上近似,L型薄片导体划分为两个矩形、两个大的对称四边形和两个小的对称四边形。已知对称四边形电阻即方块电阻,故L型薄片电阻的估算电阻为
R估=2R矩+2R方//2R方
(21)
又可知矩形部分电阻为
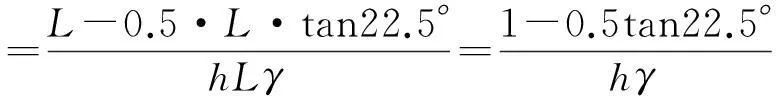
(22)
则估算电阻值为
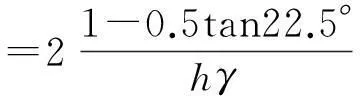
(23)
2.2非直角转角L型薄片导体电阻估算
将上一问题由直角转角推广到非直角转角。考虑如图5的等宽且转角非直角的 L型薄片导体电阻,仍设,AB=DF=BC=CD=L,∠AEF=α。同样讨论在AB边与DF边间加电压时的电阻。

图5 非直角转角L型薄片导体
近似等效分割过程与直角转角时完全类似。分割的结果如图6,同样有EG是∠AEC的角平分线,CG是∠BCE的角平分线。结论也与之前类似,同样可得到式(21)。
与直角转角时的区别在于角∠IGJ由22.5°变为0.25α。则式(23)变为
(24)
则估算结果为

(25)

图6 非直角转角L型薄片导体的分割
3估算的误差分析
对L型薄片导体,该方法的误差来源主要在两个近似,即将HI边近似为等势线和将GJ边近似为一条电流线。从近似手段分析,将某条线近似化作等势线,从物理模型上看,相当于在该面额外布置了一层理想导体,结果是改善了原导体的导电性能。同理,将某条线近似化作电流线,则相当于在该面布置了一层绝缘体,结果是降低了原来电阻的导电性能。两个手段并用可使误差在一定程度上正负相消。该方法同时利用这两种手段近似,因此能够使结果更加精确。另外应指出,转角角度α越大,这两个近似条件越接近实际。特别的,在α达到180°时,L型薄片导体退化为矩形,两个近似条件变为严格成立,此时估算值与理论值相等。
使用Matlab的PDEtool工具为仿真手段,对上述的L型薄片导体电阻数值求解,并以该结果作为精确值。
L型薄片导体的具体参数为
γ=8×106S·m-2,L=0.5m,h=0.01m。
转角分别取为α=30°,60°,90°,120°,150°,180°。其中部分仿真的图像,如α=120°时的结果,如图7所示。

图7 转角为120°的L型薄导体仿真图像
将PDEtool计算出的精确电阻值,与估算电阻
值比较,比较的结果如表1所示。
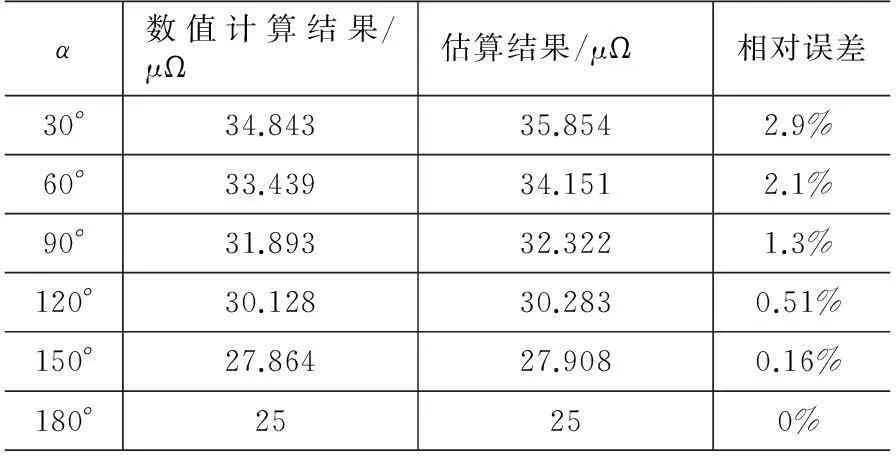
表1 非直角转角L型薄片导体的分割
可见,该方法对于转角为各种角度的L型薄片电阻,估算的误差都能保持在较小范围,而且转角越大,估算越为准确,在角度超过90°时,这种估算方法的结果已经十分接近数值计算结果。
4结语
本文首先通过理论分析推导出对于四边形薄片导体,分别在其两组对边间通电时,对应的两个电阻值的乘积总为其方块电阻的平方。在此基础上得到了关于对角线轴对称的四边形薄片导体,其对边之间电阻等于方块电阻的推论。基于上述推论,提出了对不规则形状薄片电阻的一种新的估算方法。并以L型薄片导体为例对该方法进行了理论说明和误差分析。
本文提出的估算方法具有分割简单,计算简洁,普适性强,精度较高的特点。此方法不仅可以估算转角为各种角度的L型薄片电阻,也可推广估算其他一些多边形薄片电阻。对于要求高精度的场合,该方法无法取代专业数值工具求解,但在一些追求计算简便性的场合,该方法能在简便的基础上获得较高精度的解答。
参考文献:
[1]韩金池,邹军.L型薄导体电阻的估算方法[J]. 南京:电气电子教学学报, 2012, 34(5):99-103
[2]马信山,张济世,王平编著. 电磁场基础[M]. 北京: 清华大学出版社, 1995年5月
Estimation Method of Resistance Based on Model of Axisymmetric Quadrilateral Thin Conductor
XUE Peng, ZAN Xin, ZOU Jun
(ElectricalEngineeringDept.,TsinghuaUniversity,Beijing100084,China)
Abstract:In this paper, a method of using axisymmetric thin conductor model as an equivalent to estimate corner resistance of an irregular shaped conductor is discussed. Starting from theoretical analysis, this paper demonstrates thatresistances between the opposite sides of all kinds of quadrilateral thin conductors are equal to their square resistances. Based on this conclusion, an estimation of resistance of a thin conductor which utilizes the approximate division is proposed. For instance, the method can be used to estimate resistance of an L-shaped thin conductor, and the effectiveness and accuracy of the method is analyzed and discussed when estimating.
Keywords:resistance estimation; thin resistance; square resistance
文献标识码:A
文章编号:1008-0686(2016)01-0039-04
中图分类号:TM152
作者简介:薛芃(1993-),男,在读本科生,研究方向为电力电子与电力传动,E-mail:xuep1993@sina.cn邹军(1971-),男,博士,教授,主要从事计算电磁学,电磁兼容领域教学和研究工作,E-mail:zoujun@tsinghua.edu.cn
收稿日期:2015-04-21;修回日期:2015-11- 04
