干式电压互感器匝间绝缘监测参量仿真研究

赵淼

（中国大唐集团科学技术研究总院有限公司华东电力试验研究院，合肥 230088）

0 引言

干式电压互感器因结构简单，便于维护，价格合理等优点，广泛应用于电力系统中[1]。因设计水平、浇注工艺、线材质量及运行环境等因素影响[2-3]，近年来国内各地区发生了多起因干式电压互感器内部绝缘故障而引起停电、停机事件，严重的威胁了电力系统的安全稳定性[4-5]。经统计分析，分级绝缘结构的干式电压互感器故障占比居多，并且主要由一次绕组的匝间绝缘故障引起[6-7]。

为了检测出干式电压互感器匝间绝缘故障，国内学者进行了大量研究。目前，主要检测手段有直流电阻测量[8]、空载电流测量[8]、雷电冲击耐压试验[9-10]、三倍频感应耐压试验[11]和局部放电测量[12]。当前研究重心在离线式检测方法，对于在线的匝间绝缘监测方法研究较少。针对当前研究现状，研究一种能够有效在线监测干式电压互感器匝间绝缘的方法是十分必要的。

本文通过理论分析和仿真计算，研究了干式电压互感器的一次绕组在不同位置出现单匝、多匝的短路故障时，其外部特征（等效电抗、等效阻抗模、功率因数）所呈现的变化规律，为干式电压互感器一次绕组匝间绝缘故障的在线监测提供了理论依据。

1 一次绕组分布参数模型建立

1.1 一次绕组分布参数计算

干式电压互感器一次绕组是由一根细导线同轴、多层绕制而成。各线圈本身有自感，线圈间有互感，各线圈导线有直流电阻，各线圈线匝间有匝间电容，线圈间有层间电容，内层线圈对铁心有电容，外层线圈对地有电容。

1.1.1 电感计算

一次绕组的结构特征是同轴层式，每一层线圈为一个薄壁螺线管，所以一次绕组可以表征为多层薄壁螺线管的串联。因此可以采用薄壁螺线管计算电感的方法，实现对一次绕组电感的计算[13-14]。一次绕组电感计算的简化模型见图1。

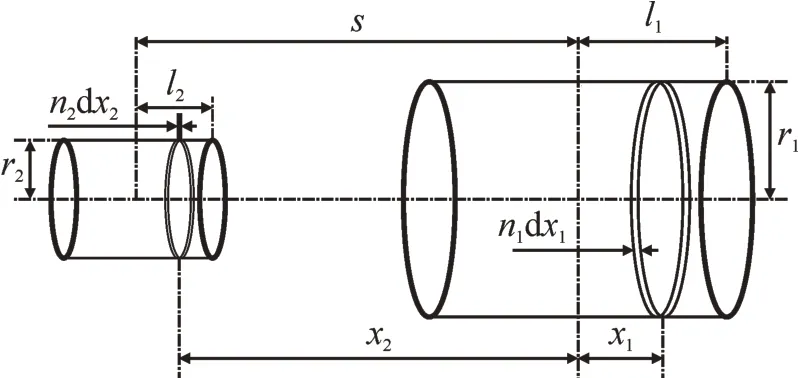
图1 一次绕组的两层线圈模型Fig.1 Two-layer coil model of primary winding

根据Neumann 公式[15]和积分原理，任意两层线圈之间电感公式为

1）当r1≠r2时，ci的表达式如下：

2）当r1=r2=r，s≠0 时，ci表达式为

3）当r1=r2=r，s=0 时，自感表达式为

式中：m为铁心磁导率；r1、r2分别表示两线圈半径；n1、n2分别表示两线圈单位长度匝数；s表示两线圈中心距离；l1和l2分别表示两线圈轴向高度一半。

1.1.2 直流电阻计算

一次绕组的直流电阻表征为每匝的直流电阻串联，则线圈直流电阻公式为

式中：ρ为导线电阻率；ri为第i层线圈半径；m为线圈匝数；S为导线横截面积。

1.1.3 电容计算

1）匝间分布电容

一次绕组线圈匝间绝缘为绝缘漆。两匝之间电容可以表征为单位长度的匝间电容串联，则匝间电容为

式中：ε为绝缘材料相对介电常数；ε0为真空介电常数；d为导线直径；D为线圈直径；a为导线匝间绝缘厚度。

2）层间分布电容

一次绕组的同轴层式结构与同轴圆柱形电容器一致[16]。利用同轴圆柱形电容器的计算方法，可得线圈层间分布电容公式为

式中：ε为绝缘材料相对介电常数；ε0为真空介电常数；rk、ri为第k、i层线圈半径；H为线圈轴向高度。

3）内层线圈对铁心之间电容

内层线圈与铁心之间电容模型与层间电容模型一致[16]。则电容公式为

式中：ε为绝缘材料相对介电常数；ε0为真空介电常数；rw为内层线圈半径；r0为铁心外半径；H为线圈轴向高度。

4）外层线圈对地电容

外层线圈下半部分与地构成电容模型是半圆柱形的。采用镜像法，可以得到外层单匝导线的单位元对地电容公式为

式中：ε0为真空介电常数；h为最外层线圈对地高度；d为导线直径。

通过对单位元加和，可得单匝线圈对地电容公式为

因积分边界问题，导致无法求取积分结果。利用高斯-勒让德积分近似求解方法，得到单匝导线对地的电容公式为

式中：ε0为真空介电常数；rn为最外层线圈半径；d为导线直径；h为最外层线圈对地高度。

1.2 模型建立

依据上述分布参数计算公式，对型号为JDZX9-20Q 的干式电压互感一次绕组进行建模，其结构参数见表1。

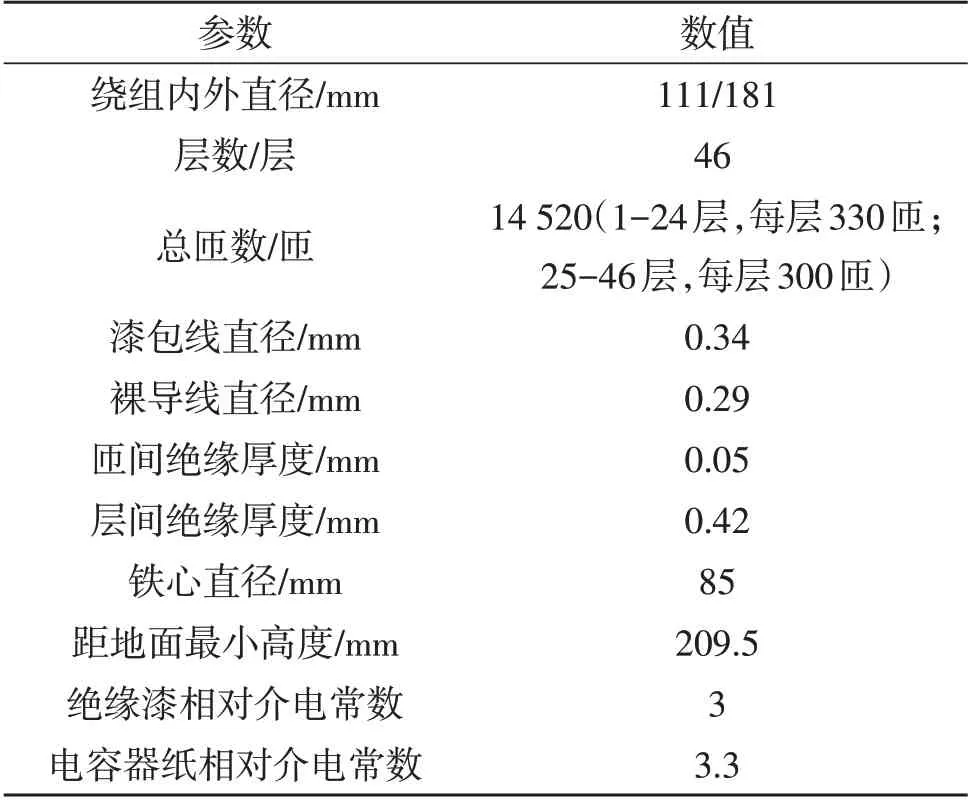
表1 一次绕组的基本参数Table 1 Basic parameters of primary winding

一次绕组每层分为3 段绕制，通过电容器纸和每段线圈相互叠加，实现了一次绕组的整体绕制，见图2。

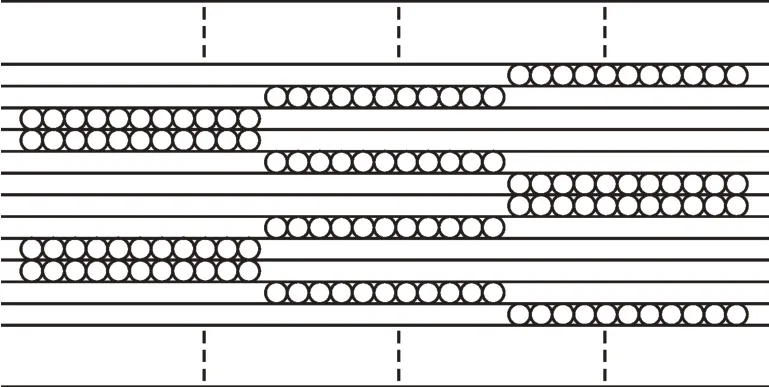
图2 一次绕组轴向截面图Fig.2 Axial section view of primary winding

结合干式电压互感器一次绕组的绕制特征，选择每层的每段线圈作为一个分析单元，建立干式电压互感器一次绕组的分布参数模型。按照从内层到外层的顺序，依次建模，见图3。图中：Ri为第i层单元线圈直流电阻；Li为第i层单元线圈自感；Ci为第i层单元线圈匝间电容；Ci,i+1为第i、i+1 层之间单元线圈层间电容；Cg1、Cg46为最内层、最外层的对地电容；Ii,j(j=1,2,3)为第i层第j单元线圈的电流，ei,j(j=1,2,3)为第i层第j单元线圈与其他单元线圈形成的感应电动势。

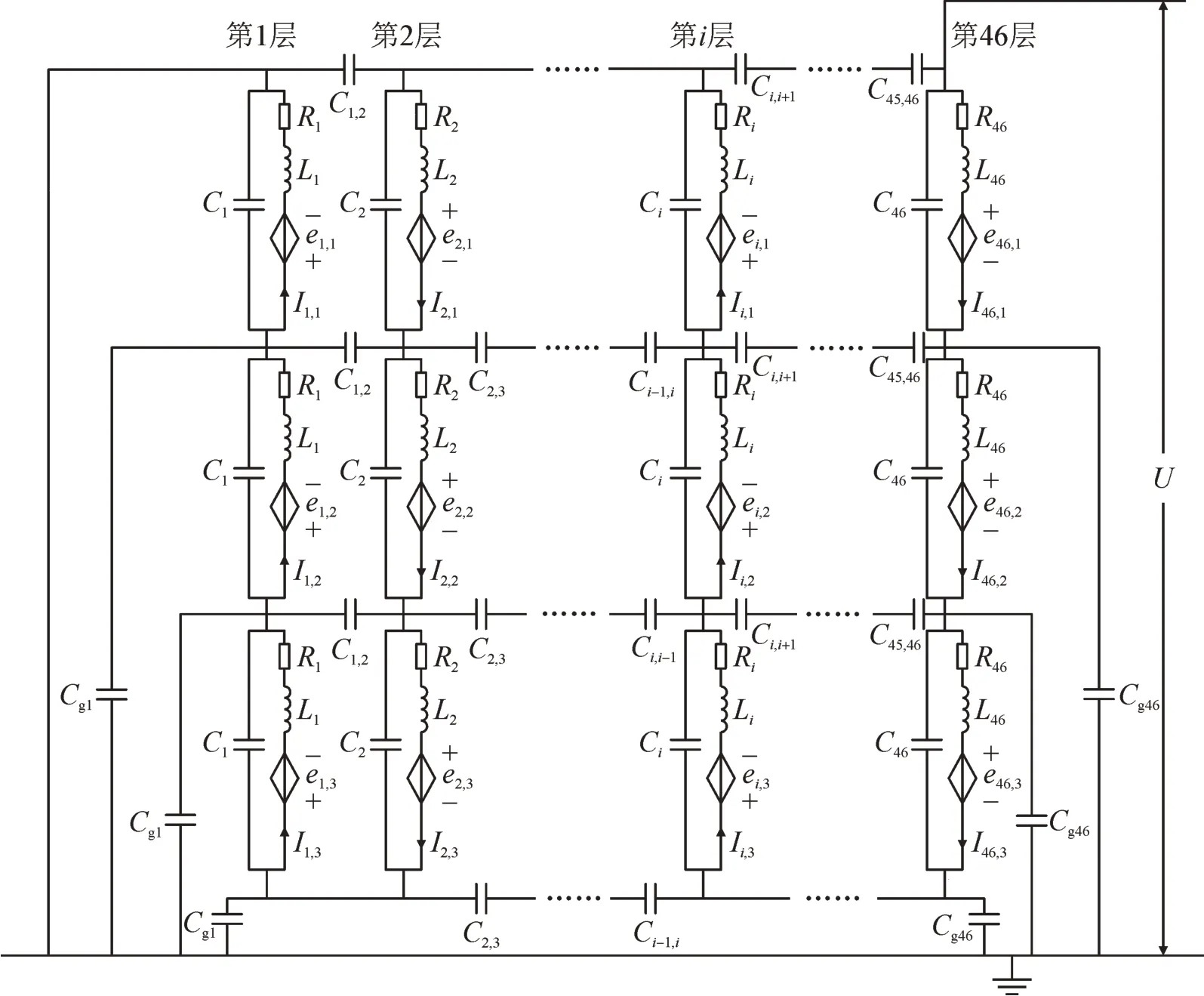
图3 干式电压互感器的分布参数模型Fig.3 Distributed parameter model of dry-type voltage transformer

2 工频下等效模型

通过参数计算可得工频下匝间电容、层间电容、对地电容的容抗非常大，即电容分流几乎为零。所以，选取无电容模型对一次绕组进行分析，选取一层线圈为一个分析单元，实现了计算的简化。当一次绕组发生匝间短路故障且短路线圈尚未融化开断之前，电路可以等效为图4。

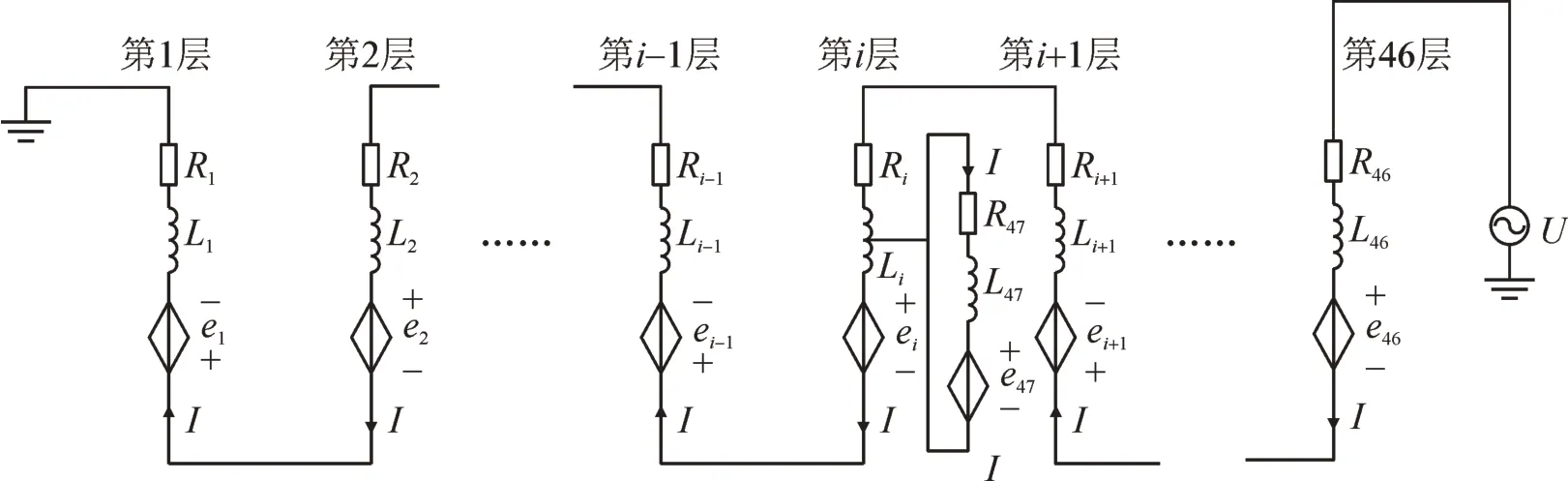
图4 短路故障等效电路Fig.4 Equivalent circuit of short-circuit fault

假设发生短路的层数为第i层，匝间绝缘损坏，导致导线金属部分直接相连。此时，第i层出现短路环，等效形成第47 层线圈。第i层线圈被短路环分割为上下两部分，且两段线圈为串联关系。同时，短路环上电压为零。由电磁感应原理可知，虽然短路环两端电压为零，但短路环内存在感应电流[17-19]。则各层之间的感应电势公式为

由此，建立图4 的电压矩阵方程为

3 匝间短路对电气参数的影响

首先对正常运行的干式电压互感器一次绕组进行仿真分析，将计算得到的等效电抗，等效阻抗模及功率因数作为基准值。然后再分别计算在不同位置（轴向不同位置和径向不同位置）出现单匝、多匝短路故障时的等效电抗、等效阻抗模、功率因数。将匝间故障参数与正常运行时的参数比较，分析匝间故障时的参数变化规律。正常运行下一次绕组的基本参数见表2。

表2 正常运行下一次绕组的基本参数Table 2 Basic parameters of the primary winding under normal operation

3.1 单匝短路故障对电气参数的影响

假设干式电压互感器运行在额定的情况下，在一次绕组的不同位置发生单匝匝间短路故障，通过仿真计算，可以得到相应的电气等效参数[22-28]。得到等效电抗、等效阻抗模、功率因数随故障位置的变化规律曲线，见图5。其横坐标为发生故障的层数，纵坐标为发生匝间故障后电气参数与正常运行下电气参数比值。故障位置：径向故障位置选择第1层（最内层）、第10 层、第19 层、第28 层、第37 层、第46 层（最外层）；轴向故障位置选择端部、1/4 处、1/2 处（中部）。由图5 可以看出：

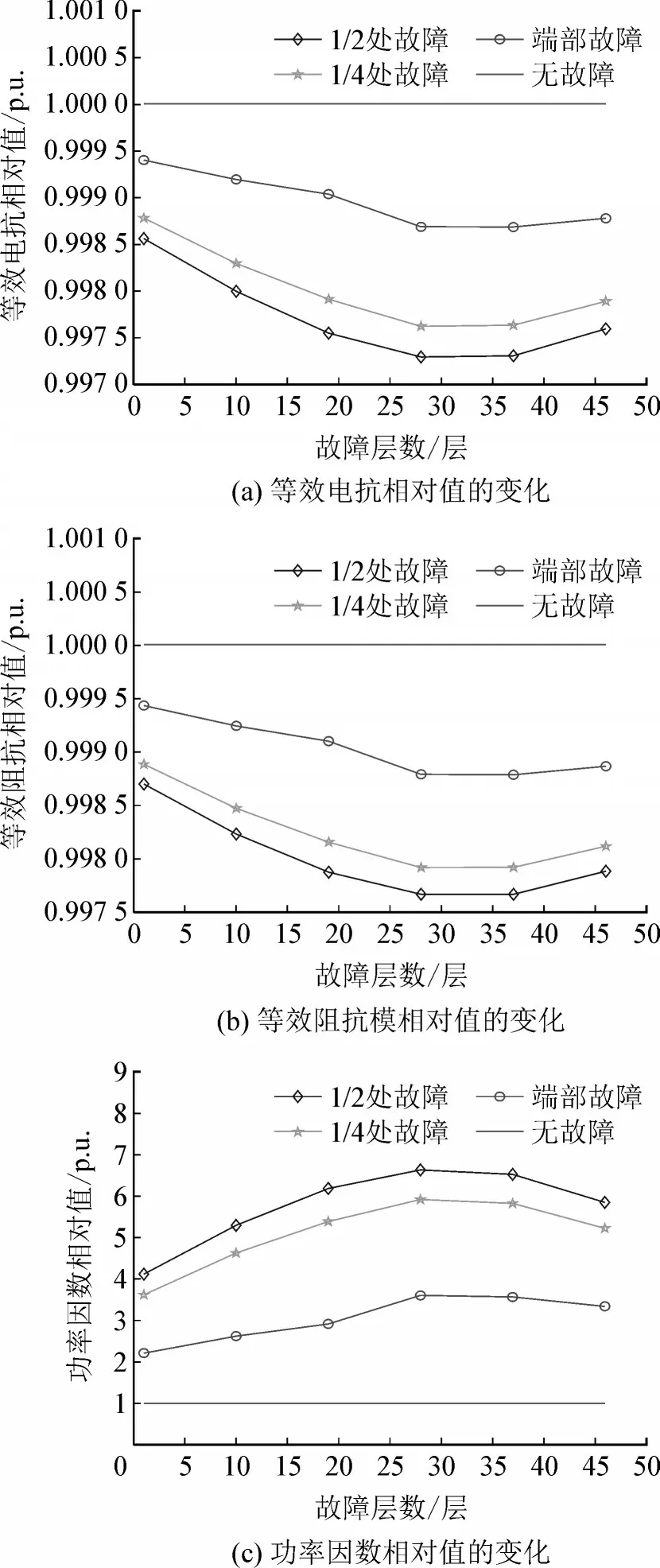
图5 电气参数相对值与故障位置的关系Fig.5 Relationship between relative value of electrical parameters and fault location

1）当一次绕组发生单匝短路故障时，功率因数相对值变化最大，等效电抗相对值和等效阻抗模相对值变化均较小。其中，功率因数相对值大于1，与正常情况下的参数相比，故障时的功率因数明显增大；等效电抗相对值和等效阻抗模相对值小于1，与正常情况下的参数相比，故障时的等效电抗和等效阻抗模幅值减小；

2）当单匝短路故障层由内层向外层变化时，功率因数相对值先增加后减少；等效电抗相对值和等效阻抗模相对值先减少后增加。当故障发生在中层时，功率因数相对值、等效电抗相对值和等效阻抗模相对值变化最大，说明中层的匝间故障，对一次绕组整体电气参数的影响最大；

3）当单匝短路故障由端部向中部变化时，功率因数相对值增加；等效电抗相对值和等效阻抗模相对值减少。当匝间短路故障位置越靠近中部时，功率因数相对值、等效电抗相对值和等效阻抗模相对值变化越大。说明靠近同层中部位置的匝间短路故障，对一次绕组的整体电气参数影响较大。

3.2 多匝短路故障对电气参数的影响

多匝短路故障的电气参数仿真，分别在轴向端部、线圈1/4 处、1/2 处（中部）设置100 匝短路线圈，其余设定与单匝短路故障完全一致。等效电抗、等效阻抗模和功率因数与不同位置故障的关系见图6。

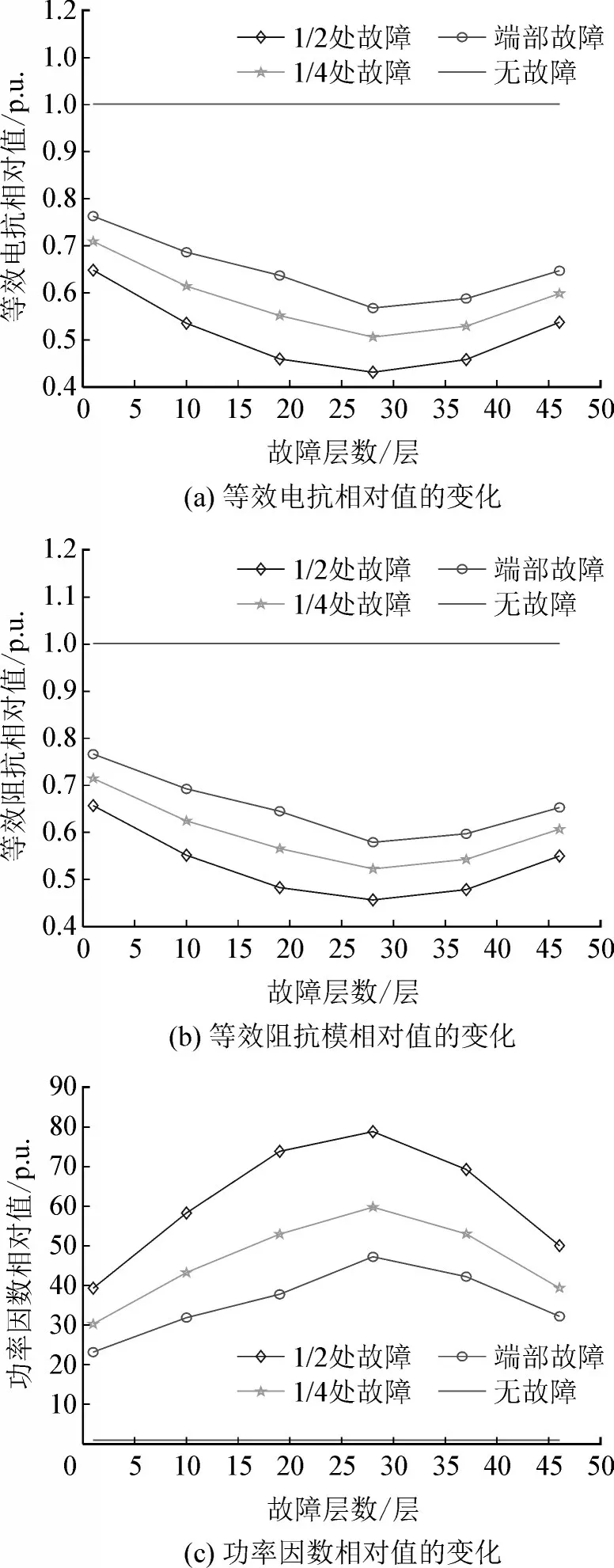
图6 电气参数相对值与故障位置的关系Fig.6 Relationship between relative value of electrical parameters and fault location

由图6 可以看出：

1）等效电抗相对值在0.431 4～0.762 3 之间变化，等效阻抗模相对值在0.456～0.765 8 之间变化，功率因数相对值在23.13～78.64 之间变化；

2）多匝短路故障和单匝短路故障的参数变化规律是一致的。功率因数相对值变化范围大，先增加后减少，等效电抗相对值和等效阻抗模相对值变化范围小，先减少后增加，且小于1。故障发生在中层中部时，对电气参数的影响最大。

3.3 故障参数对比

将单匝短路故障与多匝短路故障的电气参数进行对比，见表3。

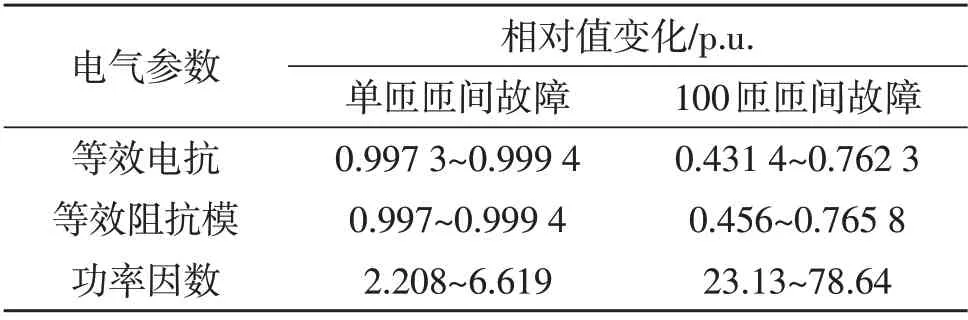
表3 电气参数比较Table 3 Comparison of electrical parameters

由表3 可以得出：

1）多匝短路故障的电气参数相对变化量大于单匝短路；

2）当发生单匝短路故障时，等效电抗、等效阻抗模的变化很微小，如作为监测参数可能导致对一次绕组匝间绝缘性能的误判；当发生单匝短路故障时，功率因数变化则大于正常值2 倍。

为研究在匝间短路期间，匝数由单匝到多匝发展过程中功率因数相对变化率的变化趋势，仿真计算了第1 层端部发生故障时，功率因数相对变化率随短路匝数的变化规律，见图7。

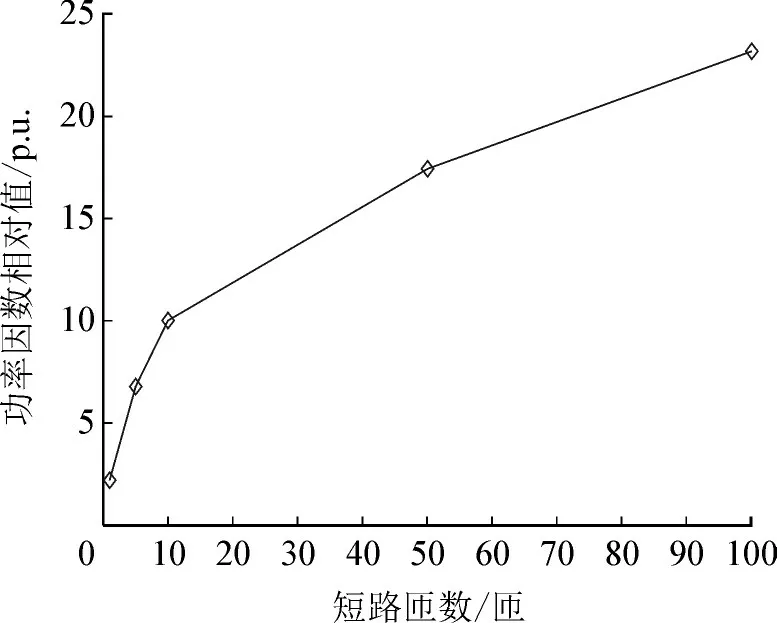
图7 功率因数变化率与短路匝数的关系Fig.7 Relationship between variation rate of power factor and short-circuit turns

由图7 可以看出：

1）功率因数相对值随着短路匝数的增加而单调增大；

2）功率因数变化率在匝间故障初期最大，随着短路匝数的增多而逐渐减小。

综上分析可知，当干式电压互感器发生匝间短路时，功率因数相对值变化明显且功率因数变化率在短路故障初期高于故障后期，因此建议将功率因数作为在线监测量。

随着行业电气量在线监测技术研究与发展，当前电流高精度小角差在线监测技术取得较大进步并在其它电气设备上进行了应用，为干式电压互感器在线监测装置的研发及应用提供了参考。

4 结语

本文研究了干式电压互感器一次绕组在不同位置出现单匝和多匝短路故障时，其电气参数所呈现的变化规律，得到以下结论：

1）当一次绕组发生匝间故障时，功率因数相对变化量最大，等效电抗和等效阻抗模相对变化量较小；多匝短路故障的电气参数相对变化量大于单匝短路；

2）当匝间故障由端部向中部变化时，功率因数相对值增加；等效电抗相对值和等效阻抗模相对值减少；故障位置越靠近中部，对一次绕组的整体电气参数影响越大；

3）当匝间故障层由内层向外层变化时，功率因数相对值先增加后减少；等效电抗相对值和等效阻抗模相对值先减少后增加；故障位置越靠近中层，对电气参数影响越大；

4）建议将功率因数变化率作为干式电压互感器一次绕组匝间绝缘在线监测的监测量。