双抽象函数问题的特殊化求解策略探析

福建省福清第三中学 (350315) 周晓玲 何 灯

抽象函数问题在近几年高考试题中频繁出现(如2021年全国新高考Ⅱ卷第8题, 2022年全国乙卷理科第12题,2022年新高考Ⅰ卷第12题,2022年新高考全国卷Ⅱ第8题等),此类问题能够很好的考查学生对函数中基本概念、基本性质的理解,考查学生综合运用所学的知识解决问题的能力,在条件的转化与策略的选择过程中考查学生的思维创新能力,导向对发展数学抽象、逻辑推理等核心素养的关注.特别是双抽象函数问题,由于问题条件的抽象性、函数关系的复杂性,求解方向的不确定性,导致学生普遍认为此类问题难以入手,往往选择直接放弃.

《孙子兵法·兵势篇》中孙子曰:“凡治众如治寡,分数是也;斗众如斗寡,形名是也”,即:治理庞大的军队如同治理少量的军队的方法,就是按一定编制将他们组织起来,让庞大军队像小队人马一样步调一致、听从指挥的方法.“治众如治寡”,这是孙子提出的一个方法论思想和一种管理学思想.将此法迁移到数学解题中,对于双抽象函数问题,我们可以尝试将两个函数分而治之,针对其中一个函数,厘清其所具有的内蕴性质,在此基础上,立意于特殊与一般思想,将其表达式特殊化和具体化,再通过两个抽象函数的关系,得到另外一个抽象函数的表达式,从而突破问题求解难点,实现问题的轻松求解.

下面以两道试题为例,阐述上述求解思想.

例1 (2023年2月福州市高三质检第8题,单选)已知函数f(x),g(x)的定义域均为R,f(x+1)是奇函数,且f(1-x)+g(x)=2,f(x)+g(x-3)=2,则( ).

A．f(x)为奇函数B．g(x)为奇函数

分析:本题中两个抽象函数纠缠在一起,正面求解需要经过了多次的代换,且多个恒等式综合在一起,导致求解思路不是那么明朗,如果学生没有经过此类问题的大量训练,势必很难完成上述过程,就算学生经过了此类问题的专门训练,也需要消耗大量的时间来摸索求解思路.注意到题设对于函数f(x)铺设的条件较多,故先尝试对f(x)进行研究.由f(x+1)是奇函数,可得f(x)图象的对称中心为(1,0).由f(1-x)+g(x)=2,f(x)+g(x-3)=2,消去g(x),得f(x+3)=f(1-x),则f(x)图象的一条对称轴为x=2.根据推导得到的f(x)的两个性质,立意于特殊与一般思想,尝试将f(x)特殊化为某个三角函数.

解析:由f(x+1)是奇函数,得y=f(x+1)图象的对称中心为(0,0),将y=f(x+1)图象向右平移一个单位,得f(x)图象的对称中心为(1,0).由f(x)+g(x-3)=2得f(x+3)+g(x)=2,结合已知条件f(1-x)+g(x)=2,可得f(x+3)=f(1-x),得f(x)图象的一条对称轴为x=2.

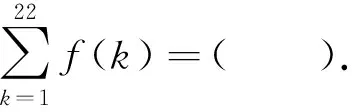
A．-21 B．-22 C．-23 D. -24

分析:本题较例1而言,两个等式右端数值不同,给加减消元后的等式的性质判定增加了难度,且增加了一个条件.本题题设对于函数g(x)铺设的条件较多,故可尝试先从g(x)入手,探明其所具有的性质.由f(x)+g(2-x)=5得f(x-4)+g(6-x)=5,将所得式子与g(x)-f(x-4)=7联立,可得g(x)+g(6-x)=12,由此可得g(x)的图象关于(3,6)对称.又y=g(x)的图象关于直线x=2对称,且g(2)=4,根据这三个条件,立意于特殊与一般思想,尝试将g(x)特殊化为某个三角函数.

解析:由f(x)+g(2-x)=5得f(x-4)+g(6-x)=5,由f(x-4)+g(6-x)=5及g(x)-f(x-4)=7,可得g(x)+g(6-x)=12,由此可得g(x)的图象关于(3,6)对称.

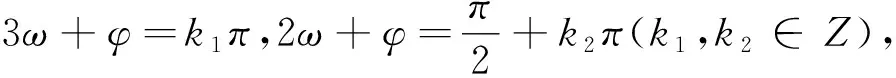
分而治之,上述解法将纠缠在一起的两个抽象函数拆分开来,通过明晰其中某个函数所具有的性质,在特殊与一般思想的引领下,构造一个特殊函数,在此基础上,实现问题的轻松求解.整个求解过程方向性明确,学生易于理解,彰显了数学思想方法在解题过程中的引领作用.在日常解题过程中,老师们应引导学生尝试换一个角度去思考问题,可能会有更深刻的认识,获得不一样的学习体验.