寻根溯源 拾级而上 提升素养
--以一轮复习“导函数的隐零点”为例
2024-01-09南京航空航天大学附属高级中学210007
南京航空航天大学附属高级中学 (210007) 戈 敏
一 引言
《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》)把函数作为贯穿高中数学课程的四大主线之一,凸显了函数在高中数学体系中的重要地位.导数作为研究函数问题的基础性工具,在解决函数单调性问题中发挥着重要作用.基于函数单调性与导函数零点的密切关系,在函数综合题的求解中对于导函数零点的处理是关键步骤.导函数的零点根据其能否精确求出分为两类,一类是能精确求出的“显零点”;一类是可以判断其存在,但难以求出或无法求出的“隐零点”.“导函数的隐零点”是教材上探究的难点问题,也是高考的热点问题.
高中数学教材浓缩了整个高中数学学科知识发展的精髓,是《标准》的物化形态与文本素材,也是《中国高考评价体系》“一核四层四翼”中的“必备知识”与“基础性”,更是实现高中育人目标、培养学生数学核心素养的重要载体.高三一轮复习应回归教材寻根溯源,拟合高考拾级而上,让学生的数学思维在“活水”滋养中一路向阳生长.本文为基于此目标做出的积极的教学实践尝试.
二 教学过程实录
1 寻根溯源,回归教材
师:本节课我们来探究函数中一类典型问题,请大家先研究人教A版选择性必修第二册104页第18题:已知函数f(x)=ex-ln(x+m),当m≤2时,求证:f(x)>0.
请大家先尝试解决以下问题:
引例 已知函数f(x)=ex-ln(x+2),求证:f(x)>0.
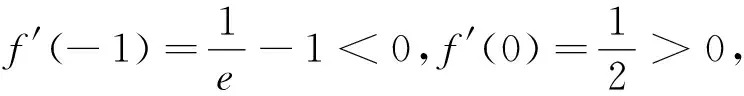
师生总结:要得到函数的单调性,需要找到导函数的隐零点x0,用零点存在定理可以解决此问题.同时,通过绘制导函数图象和原函数图象,从图象上可直观感受导函数的正负分布和原函数的最值情况.
设计意图:在导函数零点存在但不可精确求解的情况下,应用零点存在定理把该隐零点“逼”出来并设参表示,这样才可以得到导函数明确的正负分界,并得到原函数明确的增减区间.“以形探路,用形强化”可以帮助学生更好的理解函数、挖掘函数性质、提升直观想象素养,故在函数教学中提升学生的“用形”意识非常必要.
师:如何证明f(x0)>0?
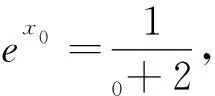
合作学习:找到症结在于“最小值f(x0)=ex0+x0,其中x0∈(-1,0)”的处理还不到位,继而找到两种解决办法:继续化简f(x0)的表达式或者缩小隐零点x0的范围.
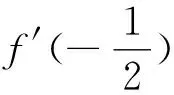
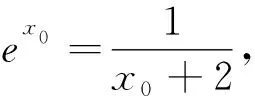
师生互动:通过对两种处理方式计算量上的对比,发现“继续化简解析式”的方法具有一定的优越性.
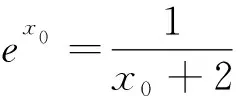
设计意图:瑞士心理学家克拉帕雷落提出“意识化原则”,即只有在不顺应时才能产生意识,只有在学习中不断造成必要的心理障碍才能取得好的效果.此处f(x0)>0的证明带来的学生认知上的冲突,有利于激发学生的求知欲和探究精神,是教师应该抓住的教育契机.根据戴尔的“经验之塔”理论,对于处于学生最近发展区的教学内容,较高效的处理方式是发挥学生的主体作用,引导学生在合作交流与实际演练中感悟出导函数隐零点的强大功能,这样既解决了函数单调区间问题,又带出了一个等式,该等式在后续的证明或者求值问题中可以实现简化解析式的妙用.同时,对于“一题多解”的问题,教师应引领学生进行方法上的优化选择,引导学生深入思考、深度剖析解析式可化简的缘由和具体持续简化的过程.
师:可以进一步缩小f(x0)的范围吗?
设计意图:在教学实践中,“学生的念头”是弥足珍贵的,教师应善于捕捉课堂即时生成的“念头”资源.在小组合作探寻f(x0)>0的证法中,不少学生尝试缩小隐零点所在范围来解决问题,虽然此法在解决本题中没有化简解析式方便,但倘若改变待证结论使得解析式化到最简仍旧无法解决问题,便应该从定义域下功夫了.“二分法”是运用函数性质求方程近似解的基本方法,“比较大小”是学生运算素养的基本体现,引导学生进一步缩小f(x0)的取值范围,有利于促使学生深入思考、深度学习,加深对隐零点知识本质的理性认识.
师:如何解决书上习题?
生7:当m≤2时,有ln(x+m)≤ln(x+2),故f(x)≥ex-ln(x+2),引例已证得ex-ln(x+2)>0,故有f(x)>0.
设计意图:教材中知识及知识生成过程蕴含着数学的质与魂,教材中的例习题使得知识运用“有章可循”、“有法可依”,其中的数学思想是促进学生能力提升素养发展的营养液,故教材是学生的知识之源和思维之源.高三复习教学应精心选择好的素材和试题,重视对解题过程的反思,捕捉学生的念头,引领学生回归学习教材,帮助学生分析问题的本质,激发高三课堂的活力,提高课堂教学的效率和品位.[3]
2 拾级而上,拟合高考
师:接下来,请大家尝试解决高考题.
(2017年全国高考数学II卷理科第21题)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0.(1)求实数a的值;(2)求证:f(x)存在唯一的极大值点x0,且e-2 设计意图:通过对教材知识和重点习题的回归,学生面对本质相同的高考题,可以依托扎实的解题经验来寻求突破,真正实现会一题、通一类,避免题海战术,达到减负增效的享受数学学习的目的. 3 凝炼升华,提升素养 生10:导函数隐零点的确定过程,要用零点存在定理合理论证,同时注意尽可能缩小隐零点所在的范围. 生11:利用隐零点方程可以化简原函数最值表达式.当问题解决不了时,可以尝试再次缩小隐零点所在范围或者将最值表达式进行进一步的化简. 生12:我们要重视教材上的习题,尤其是“综合运用”和“拓广探索”部分,里面蕴含的数学思想与方法可以帮助我们做通一类题. 设计意图:引导学生对本节课所学内容进行梳理回顾、对所用数学思想与方法进行归纳总结、对重难点做深入理解和深度思考,有利于培养学生数学概括能力和语言表达能力,帮助学生养成良好的学习习惯,助力学生实现深度学习,发展数学学科核心素养.同时,再次引导学生感受回归数学教材、研究高考题是实现高三数学复习减负增效的有效途径. 当前在高三一轮复习过程中,“回归教材”往往被“填写知识清单”或“题海复习战术”所取代,而能够进行深度教材内容回归、梳理教材不同模块之间的联系,构建整个高中数学知识体系和学科思维方法体系的低耗高效复习模式并不多见. 我国现当代著名哲学家冯契将认识过程概括为从无知到有知,从知识到智慧的两次飞跃,即通过对知识的理解、运用与体认,使知识化为主体人的思维方式与言行准则,将认知的知识转化为求知、做事和为人的素养.在高三的一轮复习中,应对教材中核心知识生成过程中蕴含的数学思想与方法进行激活、迁移、新情境运用,对重点例习题进行解题经验重组、变式训练、深度挖掘,应注重教材与真题的进阶式有机结合,抓住转识成智的良机,助力学生从知识型学习者向能力型学习者转变,促进学生思维能力与表达能力的提升,促使学科核心素养真正得以持续良性发展.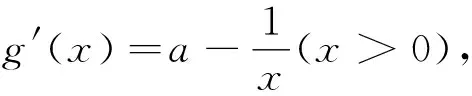
三 结语
