例析几何转化方法求解线段和差的最值问题
2024-01-09江苏省苏州市张家港市外国语学校215600董文娟
江苏省苏州市张家港市外国语学校 (215600) 董文娟
线段和差问题,在初中就是常见题型,在高中解析几何部分,也经常遇到,圆锥曲线中的动点问题,包括单动点和多动点问题,此类问题方法灵活多变,技巧性强,需要利用划归转化思想,借助三角形的三边关系.学生对此类问题往往是依题做题,没有系统的方法,容易小题大做,耗费大量时间.本文探讨如何合理转化,将原问题转化为另一个能求解的新问题,从而得到结果.
1 基本模型,化折为直
单动点问题:两定点一动点,构成三角形.三角形三边关系,是三角形三条边关系的定则,在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边.如图1,平面内两定点B、C,一动点A,有(1)AB+AC≥BC,当且仅当三点共线,且A在线段BC上时,等号成立;(2)AB-AC≤BC,当且仅当三点共线,且A在BC延长线上时,等号成立.(3)AB-AC≥-BC,当且仅当三点共线,且A在BC反向延长线上时,等号成立.
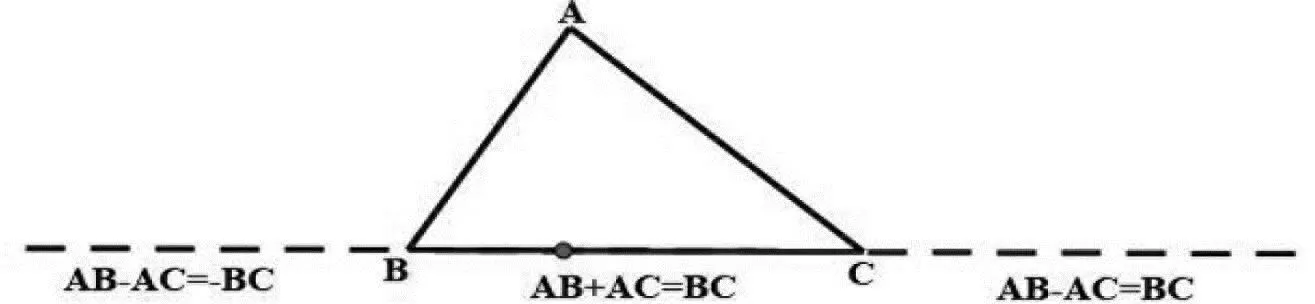
图1
根据上面三种关系,可以看出两线段和取得最小值,两线段差取最值的条件,均考虑在三点共线的时的状态.
多动点问题:其中一个动点保持运动,其它动点保持相对静止.
2 直线中的对称转化
基本模型:(1)如图2,在直线l上找一点P使得PA+PB最小.
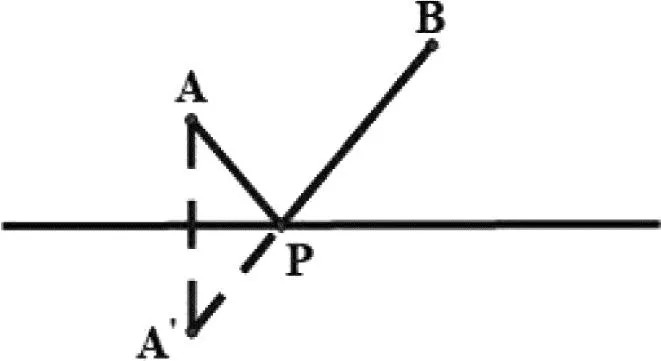
图2
(2)如图3,在直线l上找一点P使得|PA-PB|最大.
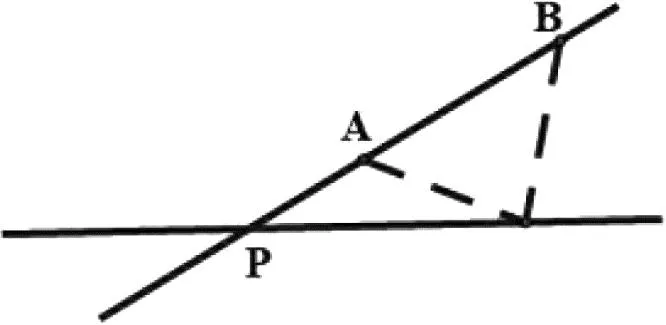
图3
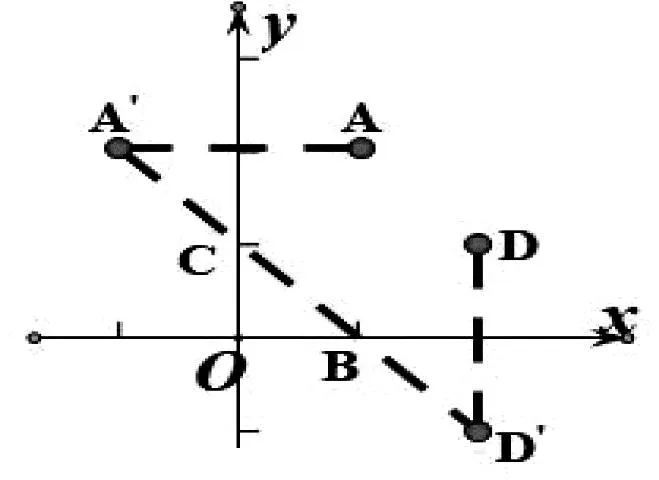
简析:(1)作点A关于直线l对称点A′,连A′B交直线l于点P,则PA+PB=PA′+PB=A′B.
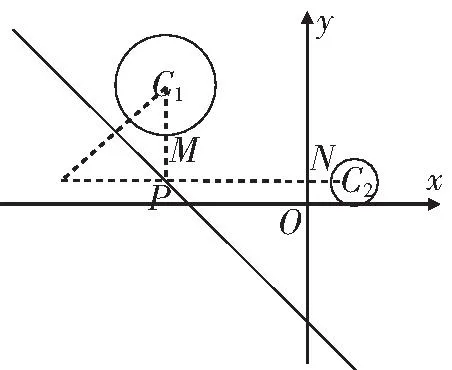
(2)当P不在直线AB上|PA-PB| 例1(1)点P在直线x-y=1上运动,A(1,-2),B(2,6),当PA-PB取最小值时,求点P坐标; (2)点A(1,2),D(2,1),B,C分别在x轴,y轴上,求AC+CB+BD的最小值; (3)点A(-1,2),B(4,-2),C(3,6),D(-2,4),P为平面内一动点,求PA+PB+PC+PD的最小值. 简析:(1)如图4,PA-PB≥-AB当P在BA延长线上,不满足,故需进行转换,作A关于直线对称点A′,则PA=PA′,PA′-PB≥-A′B,当P在BA′延长线与直线交点处,点P坐标为(-3,-4). 图5 评注:当两线段和差的最值,满足三点共线关系,可以直接求最值.若不满足三点共线的关系,则需要对线段进行合理的等价转化,对于直线上的动点问题,一般作定点关于直线的对称点转化. 到两个定点的距离之和为定值(定值大于两定点间距离)为椭圆.即PF1+PF2=2a,到两个定点的距离之差的绝对值为定值(定值小于两定点间距离)为双曲线.即|PF1-PF2|=2a,因此椭圆或双曲线上点到一个焦点的距离,可以转化为到另一个焦点的距离. 图6 图7 评注:对于动点在圆锥曲线上的线段和差问题,系数一致考虑利用另一个焦点转化,系数不一致时,系数一般是离心率的值,需要通过准线转化,变成新的线段和差问题. 图8 简析:如图9,点P,M,N均是动点,点M点N均在圆上,故将三动点问题转化为单动点问题,PM+PN≥PC1+PC2-3,因为点P在直线上,利用对称,可得最小值为9. 图9 评注:因为圆的特点,到圆上点的距离的最值,都可以转化为到圆心的距离加减半径,因此对于多动点问题,可先利用圆心转化为单动点问题,再进行处理. 线段和差的最值问题,考虑三角形的三边关系.取等条件不成立则要善于利用几何性质转化,动点一般出现在直线、圆、椭圆、双曲线、抛物线上.对于直线上动点利用对称进行转化;对于椭圆和双曲线上动点,利用可以转化到另一个焦点,系数不一致转化到准线距离;对于圆上动点,可以转化到圆心的距离.多动点问题,将圆上运动的点先固定,转化为单动点问题再处理.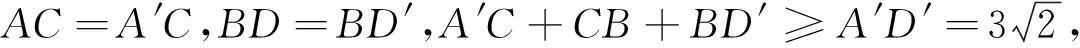
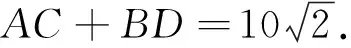
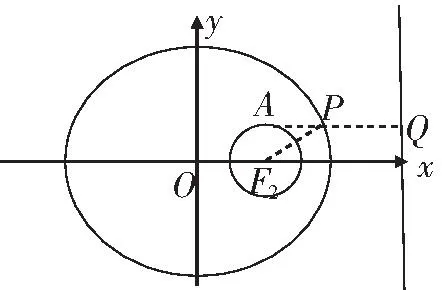
3 圆锥曲线中的定义转化

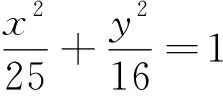
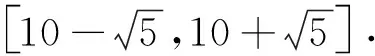
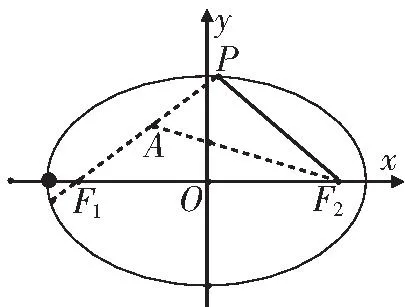
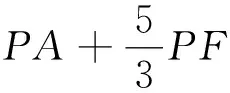
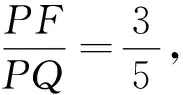
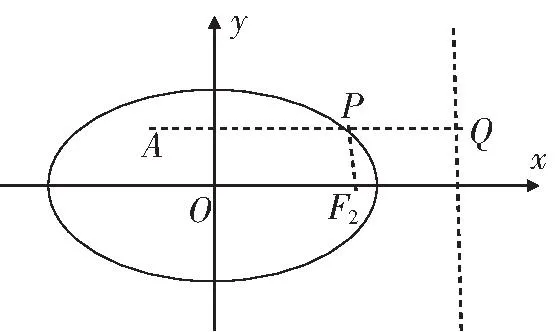
4 多动点圆心半径转化
5 结语
