问题诱发思考 任务驱动生成--以“曲线与方程”教学为例

江苏省海安市李堡中学 (226631) 田淑蓓

在数学教学中,教师应从教学实际出发,以发展学生为目标,将要学习的教学内容分解成适合本班学情的教学任务,让学生在任务的驱动下积极思考、探索、合作,并在探索与交流中获得知识、经验及方法,提高课堂教学有效性.笔者在教学“曲线与方程”时,以问题为导向,以任务为驱动,让学生亲身经历知识形成、发展、应用等过程,取得了较好的教学效果.本文将教学过程呈现如下,供参考.

一、教学实录

1、融入数学史,丰富内涵

师:任何概念、公式、定理等内容的发现与发展都需要经历一个漫长的过程,人们认识曲线和方程亦是如此,现在我们跟随着视频来了解一下解析几何的发展史.

教师播放视频,视频中介绍了古希腊数学家阿波利尼奥斯和法国数学家费马、笛卡尔的发现:阿波利尼奥斯从纯几何的观点研究圆锥曲线的性质;费马和笛卡尔虽然其研究的出发点不同,不过他们通过建立坐标系将方程与曲线联系在一起,创立了解析几何.

设计意图:将数学史融于数学课堂,让学生知晓数学知识形成是一个漫长而曲折的过程,有利于学生树立正确的数学观.另外,通过数学史让学生了解数学家研究曲线的方法,有利于学生更好地理解数学.同时有效地融入数学史,让数学课堂散发着浓浓的文化味,有利于学生数学学习热情,提高课堂教学品质[1].

2、合作交流,生成概念

探究活动1:在平面直角坐标系中,画出方程2x2-y=0(x≠0)的对应曲线.

问题给出后,教师预留时间让学生动手作图.

师:说一说,你是用什么方法画曲线的?

生齐声答:描点法.

师:那么曲线上点的坐标从何而来?

生1:解方程得来的.

师:刚刚在画图时我们挖掉了原点,说来说一说,为什么要这么操作呢?

生2:因为方程有一个限定条件“x≠0”,由此可以判定该曲线不过坐标原点,所以在画图时应该挖掉原点.

师:非常好,想得很周全.若不挖掉原点,你认为是以方程的解为坐标的点的个数多,还是曲线上点的个数多呢?

生3:我认为是曲线上的点多,多了一个原点.

师:刚刚用描点法得到了曲线的大致图形,是否可以说方程上所有的解为坐标的点都在曲线上呢?

生4:应该成立,以前作图也是这样做的.

接下来教师用几何画板演示,验证以上说法是正确的.

设计意图:让学生通过动手画体会方程与曲线间的内在联系,经历由数到形的转化为学生理解方程的曲线提供了依据.

探究活动2:如图1,请写出该曲线的对应方程.

图1

问题给出后,很快学生就给出了答案:x-y+2=0(x≠-1).

师:谁来说一说,你是如何求曲线的方程的呢?

生1:由图1可知,直线过(-2,0)和(0,2)两点,根据两点式得直线方程为x-y+2=0(x≠-1).

师:很好,是不是直线上所有的点的坐标都在曲线方程x-y+2=0(x≠-1)上呢?

生5:应该是吧.

接下来,教师继续用几何画板进行演示,让学生更加直观地感知点的坐标始终满足所求方程.

师:如果所求直线方程没有x≠-1这一限制条件,你认为是以方程的解为坐标的点的个数多,还是曲线上点的个数多呢?

生齐声答:应该是方程的解多.

设计意图:通过由形到数的转化,让学生更加直观地体会曲线上的点的坐标与所求方程的解的对应关系,为学生理解曲线的方程提供依据.

探究活动3:请按照要求画如下曲线:①曲线C:到点O(0,0)距离为1的圆,且在y轴右侧部分的曲线;②方程f(x,y)=0:x2+y2=1(y>0)表示的曲线.

师:结合图形想一想,曲线C上的点的集合与方程f(x,y)=0的解是否存在包含关系?

生齐声答:不存在.

师:很好,这就说明曲线与方程不能建立某种对应关系.

设计意图:通过思考辨析让学生不仅理解概念的内涵,而且掌握概念的外延,为后期概念的灵活应用打下坚实的基础.

师:结合以上3个探究请大家想一想,若使方程和曲线可以相互表示,需要满足什么条件呢?(生积极交流)

生6:以方程的解为坐标的点与曲线上的点的数量一样多.

师:非常好,通过经历由数到形和由形到数的转化,我们知道以方程的解为坐标的点与曲线上的点间存在一一对应的关系,若想它们同时成立,就要确保其在数量上是一致的.

在此基础上,教师给出方程与曲线的定义也就水到渠成了.

设计意图:以丰富的实例为依托,让学生通过观察、对比、抽象等过程揭示概念的本质属性,培养学生数学抽象概括素养[2].

3、任务驱动,深化理解

探究活动4:如图2,以下方程与曲线是否一致,如果不一致,是否可以通过修改其中一个使方程变成曲线的方程,而曲线变成方程的曲线呢?

设计意图:通过具体练习引导学生思考、辨析,以此深化概念理解.在此基础上,通过修改方程或曲线来自动建立一一对应的关系,促进学生对方程与曲线概念的再认识与升华.

师:在判断曲线与方程不对应时,有时只要举一个反例即可,而在判断两者对应时需要严格证明.对于题(4),若要说明方程与曲线的一一对应关系,你认为该如何证明呢?

生7:应从两方面证明,既要证明曲线上的点是方程的解,还要证明方程的解是曲线上的点.

对于题4的证明,学生不知如何入手,教师进一步引导,将问题具体化,给出如下问题:证明:以坐标原点为圆心,半径为1的圆的方程是x2+y2=1.

问题给出后,教师预留充足的时间让学生思考与交流,然后点明让学生简述他的证明过程.

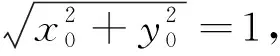
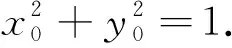
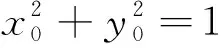
设计意图:通过以上环节的设计,让学生通过亲历命题的证明过程进一步理解方程与曲线的概念.同时,通过数形结合思想方法的渗透,有利于激发学生的探究热情,促进学生数学思维的发展.另外,通过以上探究让学生明白,数学是一门严谨的学科,若想证明一个结论是否正确需要给出严谨的证明,以此培养思维的严谨性.

4、课堂小结,升华认知

师:通过本节课的学习,你收获了哪些知识和方法呢?

该环节教师以生生交流为主,在适当的时机进行点拨与评价,然后结合学生交流结果,给出图3.

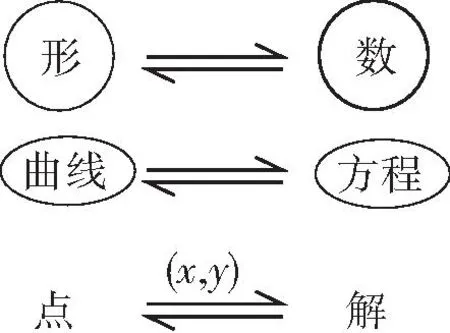
图3

设计意图:通过课堂小结引导学生梳理知识,形成方法,积累经验,以此达到深化理解,升华认知的效果.

二、教学思考

在新课程的推动下,高中数学课堂教学越来越关注于学生数学综合素养的提升.教学中,教师应重视数学文化的渗透,充分发挥数学文化的育人功能,激发学生数学研究热情.

本课教学中,教师结合教学实际有目的、有针对性地设计探究性的问题情境,让学生通过经历由数到形、由形到数、数形互化等过程更好地理解概念,提升学生的数学抽象素养[3].同时,在此过程中,教师引导学生进行思考辨析,以此揭示概念的本质,发展学生的数学逻辑推理能力.

总之,在数学教学中,教师要不断更新教学观念,与时俱进,充分发挥教师启发者和组织者的作用,从学生思维的最近发展区出发,设计符合教学实际的问题情境,启发学生思考,暴露学生的思维过程,以此通过有效的点拨帮助学生突破教学重难点,提高课堂教学效率.