对一道解析几何模拟题的探究*

江西省南昌市第十中学 (330006) 龙泽南

江西省南昌市铁路第一中学 (330002) 章建荣

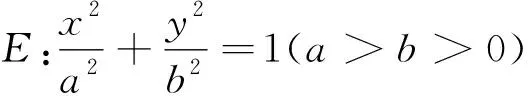
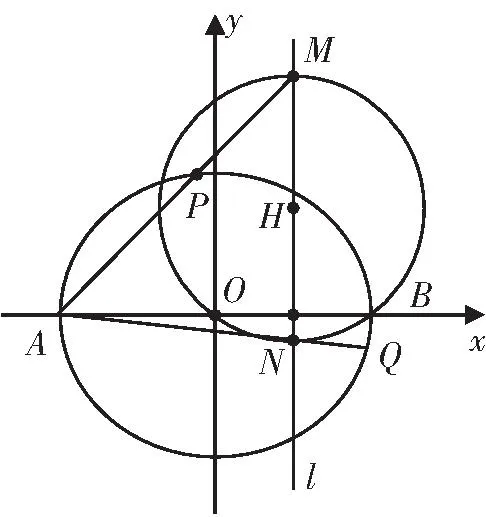
图1

如图2-4,模拟试题首先是过椭圆长轴上的定点的直线与椭圆相交于P,Q两点,再过椭圆的左顶点A,作直线AP,AQ与定直线x=n相交于M,N两点,观察以MN为直径的圆,发现此圆会过x轴上的两个定点,如果不是从椭圆的左顶点A出发引双线则该圆不过的定点,同时进一步探究发现,取圆的圆心为H,直线PQ与直线OH的斜率(斜率存在)之积也为定值.

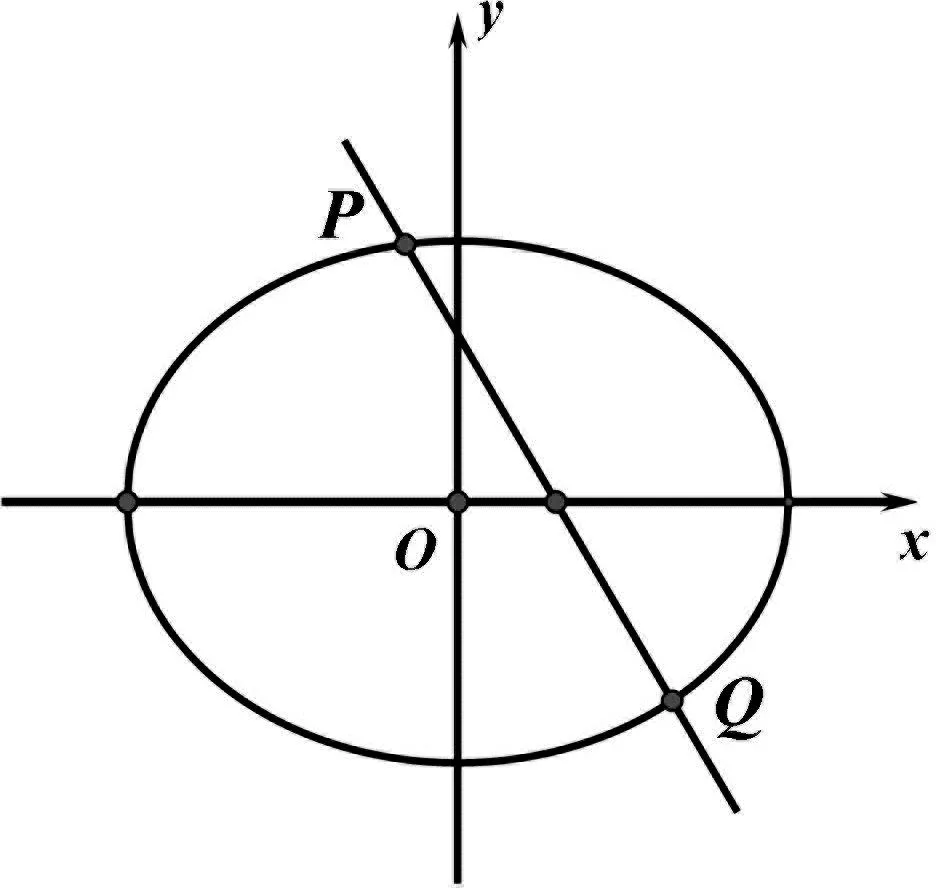
图2

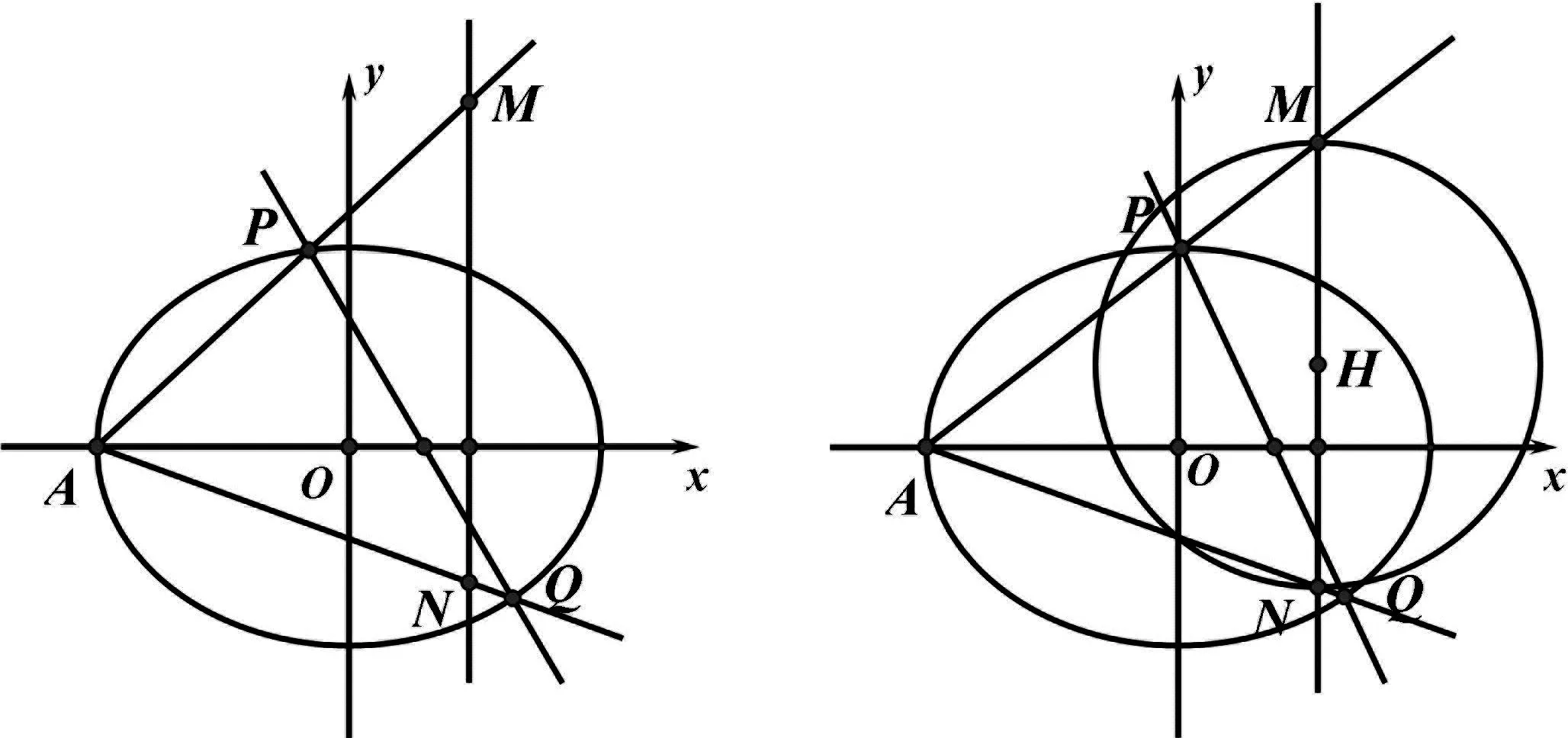
图3 图4

该题以直线过定点为背景,进行了一系列探究,得出了一个结论.

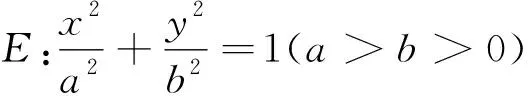
(1)以MN为直径的圆恒过两个定点

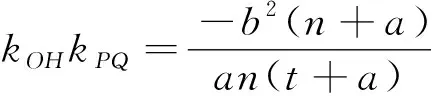
图5

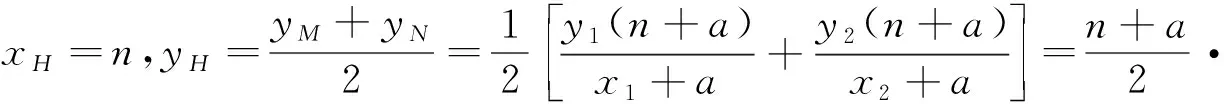
结论1是在椭圆的对称性和直线过定点条件下探究得到,那么双曲线和抛物线是否也有这样类似的结论呢?我们利用几何画板,进行了进一步探究发现了下列一系列结论,下面将结论从椭圆中推广至双曲线和抛物线也得出类似的结论.

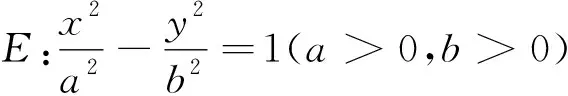
(1)以MN为直径的圆恒过两个定点

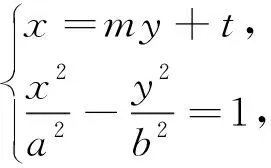
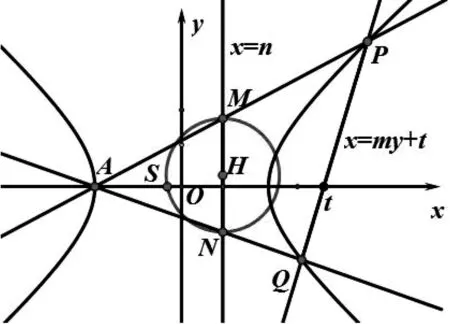
图6

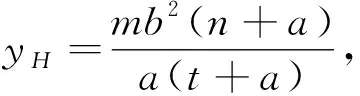
类似,对于抛物线情形,可证得如下结论,证明过程略.

结论3 如图7,已知抛物线E:y2=2px(p>0)的顶点为O,过x轴上一定点(t,0)(t>0)的直线与抛物线E相交于P,Q两点,直线OP,OQ分别与直线l:x=n相交于M,N两点.

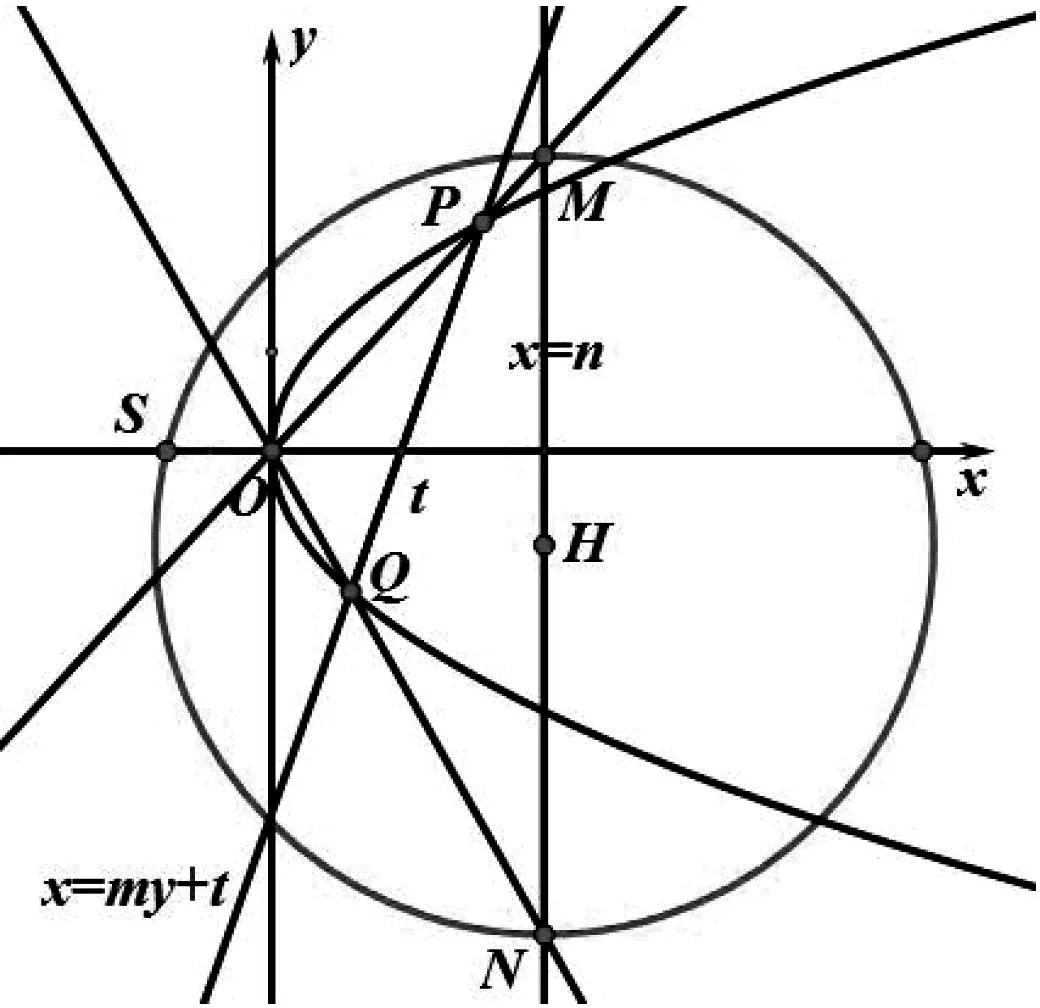
图7

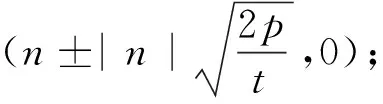
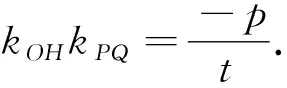
在这一探究中,我们建立了动直线过定点、斜率之积为定值、动圆过定点三者的联系,大家还可以改变条件,已知其中一个“定”,去探究另外两个“定”,没有“无中生有”的定值,我们要应该主动去发现定值背后的“因”,不断拓展我们的认识.